- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
紫色彗星数学竞赛真题(2009年高中组)
PURPLE COMET MATH MEET April 2009
HIGH SCHOOL - PROBLEMS
Copyright Titu Andreescu and Jonathan Kane
Problem 1
In fifive years, Tom will be twice as old as Cindy. Thirteen years ago, Tom was three times as old as Cindy. How many years ago was Tom four times as old as Cindy?
Problem 2
Find the least positive integer n such that for every prime number p, p2 + n is never prime.
Problem 3
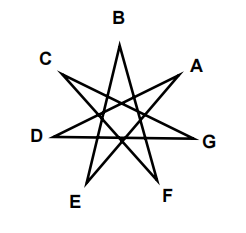
In the diagram ABCDEF G is a regular heptagon (a 7 sided polygon). Shown is the star AEBF CGD. The degree measure of the obtuse angle formed by AE and CG is ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
Problem 4
There are three bags of marbles. Bag two has twice as many marbles as bag one. Bag three has three times as many marbles as bag one. Half the marbles in bag one, one third the marbles in bag two, and one fourth the marbles in bag three are green. If all three bags of marbles are dumped into a single pile, ![]() of the marbles in the pile would be green where m and n are relatively prime positive integers.
of the marbles in the pile would be green where m and n are relatively prime positive integers.
Find m + n.
Problem 5
Find n so that ![]()
Problem 6
Wiles county contains eight townships as shown on the map. If there are four colors available, in how many ways can the the map be colored so that each township is colored with one color and no two townships that share a border are colored with the same color?
Problem 7
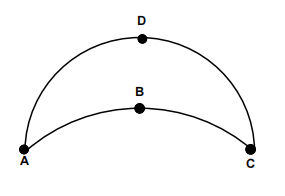
The fifigure ABCD is bounded by a semicircle CDA and a quarter circle ABC.
Given that the distance from A to C is 18, fifind the area of the fifigure.
Problem 8
Find the least positive integer that has exactly 20 positive integer divisors.
Problem 9
Bill bought 13 notebooks, 26 pens, and 19 markers for 25 dollars. Paula bought 27 notebooks, 18 pens, and 31 markers for 31 dollars. How many dollars would it cost Greg to buy 24 notebooks, 120 pens, and 52 markers?
Problem 10
Towers grow at points along a line. All towers start with height 0 and grow at the rate of one meter per second. As soon as any two adjacent towers are each at least 1 meter tall, a new tower begins to grow at a point along the line exactly half way between those two adjacent towers. Before time 0 there are no towers, but at time 0 the fifirst two towers begin to grow at two points along the line. Find the total of all the heights of all towers at time 10 seconds.
Problem 11
The four points A(−1, 2), B(3, −4), C(5, −6), and D(−2, 8) lie in the coordinate plane. Compute the minimum possible value of P A + P B + P C + P D over all points P.
Problem 12
What is the least possible sum of two positive integers a and b where a · b = 10! ?
Problem 13
Greta is completing an art project. She has twelve sheets of paper: four red, four white, and four blue. She also has twelve paper stars: four red, four white, and four blue. She randomly places one star on each sheet of paper. The probability that no star will be placed on a sheet of paper that is the same color as the star is ![]() where m and n are relatively prime positive integers. Find n − 100m.
where m and n are relatively prime positive integers. Find n − 100m.
Problem 14
Let ABCD be a trapezoid with AB parallel to CD, AB has length 1, and CD has length 41. Let points X and Y lie on sides AD and BC, respectively, such that XY is parallel to AB and CD, and XY has length 31. Let m and n be two relatively prime positive integers such that the ratio of the area of ABY X to the area of CDXY is ![]() . Find m + 2n.
. Find m + 2n.
Problem 15
What is the remainder when 789 is divided by 1000?
Problem 16
Let the complex number z = cos![]() + i sin
+ i sin![]() . Find the smallest positive integer n so that zn has an imaginary part which exceeds
. Find the smallest positive integer n so that zn has an imaginary part which exceeds ![]() .
.
Problem 17
How many ordered triples (a, b, c) of odd positive integers satisfy a + b + c = 25?
Problem 18
On triangle ABC let D be the point on AB so that CD is an altitude of the triangle, and E be the point on BC so that AE bisects angle BAC. Let G be the intersection of AE and CD, and let point F be the intersection of side AC and the ray BG. If AB has length 28, AC has length 14, and CD has length 10, then the length of CF can be written as ![]() where k, m, n, and p are positive integers, k and n are relatively prime, and p is not divisible by the square of any prime. Find k − m + n + p.
where k, m, n, and p are positive integers, k and n are relatively prime, and p is not divisible by the square of any prime. Find k − m + n + p.
Problem 19
If a and b are complex numbers such that a2 + b2 = 5 and a3 + b3 = 7, then their sum, a + b, is real. The greatest possible value for the sum a + b is ![]() where m and n are integers. Find n.
where m and n are integers. Find n.
Problem 20
Five men and seven women stand in a line in random order. Let m and n be relatively prime positive integers so that ![]() is the probability that each man stands next to at least one woman. Find m + n.
is the probability that each man stands next to at least one woman. Find m + n.
Problem 21
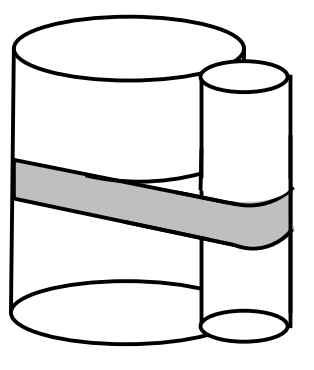
A cylinder radius 12 and a cylinder radius 36 are held tangent to each other with a tight band. The length of the band is ![]() + nπ where m, k, and n are positive integers, and k is not divisible by the square of any prime. Find m + k + n.
+ nπ where m, k, and n are positive integers, and k is not divisible by the square of any prime. Find m + k + n.
Problem 22
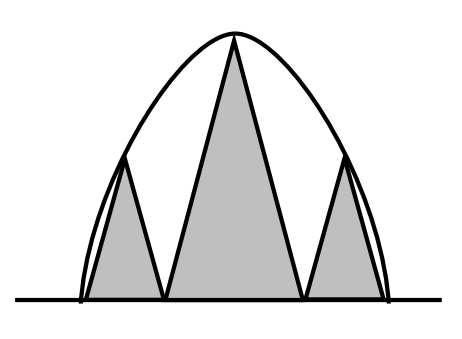
The diagram shows a parabola, a line perpendicular to the parabola’s axis of symmetry, and three similar isosceles triangles each with a base on the line and vertex on the parabola. The two smaller triangles are congruent and each have one base vertex on the parabola and one base vertex shared with the larger triangle. The ratio of the height of the larger triangle to the height of the smaller triangles is ![]() where a, b, and c are positive integers, and a and c are relatively prime. Find a + b + c.
where a, b, and c are positive integers, and a and c are relatively prime. Find a + b + c.
Problem 23
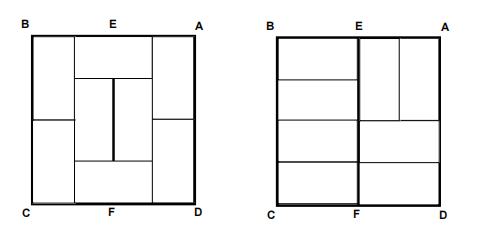
Square ABCD has side length 4. Points E and F are the midpoints of sides AB and CD, respectively. Eight 1 by 2 rectangles are placed inside the square so that no two of the eight rectangles overlap (see diagram). If the arrangement of eight rectangles is chosen randomly, then there are relatively prime positive integers m and n so that ![]() is the probability that none of the rectangles crosses the line segment EF (as in the arrangement on the right). Find m + n.
is the probability that none of the rectangles crosses the line segment EF (as in the arrangement on the right). Find m + n.
Problem 24
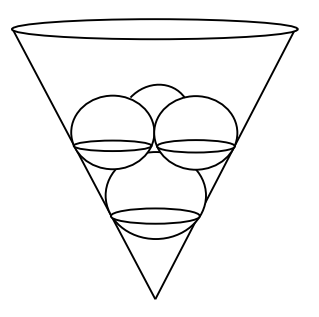
A right circular cone pointing downward forms an angle of 60◦ at its vertex. Sphere S with radius 1 is set into the cone so that it is tangent to the side of the cone. Three congruent spheres are placed in the cone on top of S so that they are all tangent to each other, to sphere S, and to the side of the cone. The radius of these congruent spheres can be written as ![]() where a, b, and c are positive integers such that a and c are relatively prime. Find a + b + c.
where a, b, and c are positive integers such that a and c are relatively prime. Find a + b + c.
Problem 25
The polynomial P(x) = a0 + a1x + a2x2 +… + a8x8 + 2009x9 has the property
that ![]() for k = 1, 2, 3, 4, 5, 6, 7, 8, 9. There are relatively prime positive integers m and n such that
for k = 1, 2, 3, 4, 5, 6, 7, 8, 9. There are relatively prime positive integers m and n such that ![]() . Find n − 10m.
. Find n − 10m.
扫描下方二维码获取本年度学术活动答案及解析
还可免费领取最新年度真题及答案解析



最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








