紫色彗星数学竞赛真题（2008年高中组）

PURPLE COMET MATH MEET– April 2008

HIGH SCHOOL – PROBLEMS

© Copyright Titu Andreescu and Jonathan Kane

Problem 1

What is the least positive integer with the property that the product of its digits is 9! ?

 

Problem 2

A canister contains two and a half cups of flour. Greg and Sally have a brownie recipe which calls for one and one third cups of flour. Greg and Sally want to make one and a half recipes of brownies. To the nearest whole percent, what percent of the flour in the canister would they use?

 

Problem 3

Find the least integer n greater than 345 such that

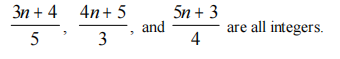 and are all integers.

 

Problem 4

The student population at one high school consists of freshmen, sophomores, juniors, and seniors. There are 25 percent more freshmen than juniors, 10 percent fewer sophomores than freshmen, and 20 percent of the students are seniors. If there are 144 sophomores, how many students attend the school?

 

Problem 5

Find the sum of all the digits in the decimal representations of all the positive integers less than 1000.

 

Problem 6

Three friends who live in the same apartment building leave the building at the same time to go rock climbing on a cliff just outside of town. Susan walks to the cliff and climbs to the top of the cliff. Fred runs to the cliff twice as fast as Susan walks and climbs the top of the cliff at a rate that is only two-thirds as fast as Susan climbs. Ralph bikes to the cliff at a speed twice as fast as Fred runs and takes two hours longer to climb to the top of the cliff than Susan does. If all three friends reach the top of the cliff at the same time, how many minutes after they left home is that?

 

Problem 7

A line through the origin passes through the curve whose equation is 5y=2x² - 9x + 10 at two points whose x-coordinates add up to 77. Find the slope of the line.

 

Problem 8

A container is shaped like a square-based pyramid where the base has side length 23 centimeters and the height is 120 centimeters. The container is open at the base of the pyramid and stands in an open field with its vertex pointing down. One afternoon 5 centimeters of rain falls in the open field partially filling the previously empty container. Find the depth in centimeters of the rainwater in the bottom of the container after the rain.

 

Problem 9

Find the sum of all the integers N > 1 with the properties that the each prime factor of N is either 2, 3, or 5, and N is not divisible by any perfect cube greater than 1.

 

Problem 10

There are three men and eleven women taking a dance class. In how many different ways can each man be paired with a woman partner and then have the eight remaining women be paired into four pairs of two?

 

Problem 11

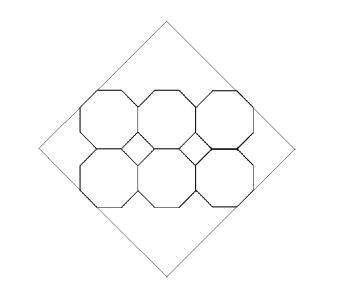
Six regular octagons each with sides of length 2 are placed in a two-by-three array and inscribed in a square as shown. The area of the square can be written in the form where m and n are positive integers. Find m + n.

Problem 12

We record one number every workday: Monday, Tuesday, Wednesday, Thursday, and Friday. On the first Monday the number we record is ten and a half. On every Tuesday and every Thursday the number we record is one third of what it was on the previous workday. On every Monday, Wednesday, and Friday the number we record is double what it was on the previous workday. This will go on forever. What is the sum of all of the numbers we will record?

 

Problem 13

If you roll six fair dice, let p be the probability that exactly five different numbers appear on the upper faces of the six dice. If p = where m and n are relatively prime positive integers, find m + n.

 

Problem 14

A circular track with diameter 500 is externally tangent at a point A to a second circular track with diameter 1700. Two runners start at point A at the same time and run at the same speed. The first runner runs clockwise along the smaller track while the second runner runs clockwise along the larger track. There is a first time after they begin running when their two positions are collinear with the point A. At that time each runner will have run a distance of  where m and n are relatively prime positive integers. Find m + n.

 

Problem 15

 

Problem 16

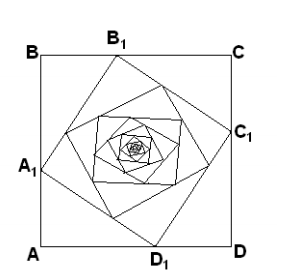
Square ABCD has side length 7. Let A ₁,B₁ , C₁ , and D₁ be points on rays , respectively, where each point is 3 units from the end of the ray so that A1B1C1D1 forms a second square as shown. Similarly, let A₂ , B₂ , C₂ , and D₂ be points on segments A ₁B₁ , B₁ C₁ , C₁D₁  and D ₁A ₁ , respectively, forming another square where A₂ divides segment A ₁B₁ into two pieces whose lengths are in the same ratio as AA₁ is to A ₁B. Continue this process to construct square AnBnCnDn for each positive integer n. Find the total of all the perimeters of all of the squares..

Problem 17

24! = 620,448,401,733,239,439,360,000 ends in four zeros, and 25! =15,511,210,043,330,985,984,000,000 ends in six zeros. Thus, there is no integer n such that n! ends in exactly five zeros. Let S be the set of all k such that for no integer n does n! end in exactly k zeros. If the numbers in S are listed in increasing order, 5 will be the first number. Find the 100^th number in that list.

 

Problem 18

The diagram below contains eight line segments, all the same length. Each of the angles formed by the intersections of two segments is either a right angle or a 45 degree angle. If the outside square has area 1000, find the largest integer less than or equal to the area of the inside square.

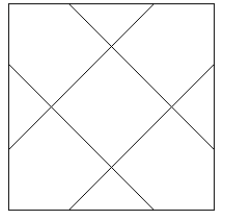
Problem 19

One side of a triangle has length 75. Of the other two sides, the length of one is double the length of the other. What is the maximum possible area for this triangle?

 

Problem 20

Find the least positive integer n such that the decimal representation of the binomial coefficient ends in four zero digits.

 

Problem 21

The area of the quadrilateral with vertices at the four points in three dimensional space (0,0,0), (2,6,1), (–3,0,3), and (–4, 2, 5) is the number , where m and n  are relatively prime positive integers. Find m + n.

 

Problem 22

Let★be a binary operation on the natural numbers satisfying the properties that, for all a, b, and c,

(a + b) ★ c = (a ★ c) + (b ★ c) and a ★ (b + c) = (a ★b) ★ c.

Given that 5 ★ 5 = 160, find the value of 7 ★ 7.

 

Problem 23

Circle B, which has radius 2008, is tangent to horizontal line A at point P. Circle C₁ has radius 1 and is tangent both to circle B and to line A at a point to the right of point P. Circle C2 has radius larger than 1 and is tangent to line A and both circles B and C₁ . For n > 1, circle C_n is tangent to line A and both circles B and C_n-1. Find the largest value of n such that this sequence of circles can be constructed through circle C_n where the n circles are all tangent to line A at points to the right of P.

 

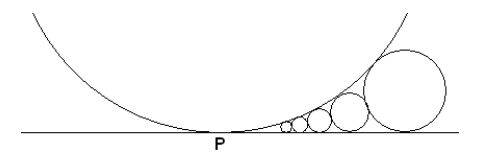
Problem 24

Each of the distinct letters in the following addition problem represents a different digit. Find the number represented by the word MEET.

 

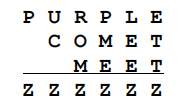
Problem 25

Let S be a point chosen at random from the interior of the square ABCD, which has side AB and diagonal AC. Let P be the probability that the segments AS, SB, and AC are congruent to the sides of a triangle. Then P can be written as 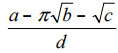where a, b, c, and d are all positive integers and d is as small as possible. Find a b + c d.

 

扫描下方二维码获取本年度学术活动答案及解析

还可免费领取最新年度真题及答案解析