紫色彗星数学竞赛真题（2007年高中组）

PURPLE COMET MATH MEET– April 2007

HIGH SCHOOL – PROBLEMS

© Copyright Titu Andreescu and Jonathan Kane

Problem 1

The sum of nine consecutive odd numbers is 2007. Find the greatest of these nine numbers.

 

Problem 2

A positive number has the property that it is equal to the ratio of 7 plus the number’s reciprocal and 65 minus the number’s reciprocal. Given that m and n  are relatively prime positive integers, find 2m + n.

 

Problem 3

A bowl contained 10% blue candies and 25% red candies. A bag containing three quarters red candies and one quarter blue candies was added to the bowl. Now the bowl is 16% blue candies. What percentage of the candies in the bowl are now red?

 

Problem 4

To the nearest degree, find the measure of the largest angle in a triangle with side lengths 3, 5, and 7.

 

Problem 5

F(0) = 3 and F n= F  ( n-1) +4 when n is positive.Find

 

Problem 6

Find the sum of all the positive integers that are divisors of either 96 or 180.

 

Problem 7

Allowing x to be a real number, what is the largest value that can be obtained by the function 25 sin(4x) – 60 cos (4x)?

 

Problem 8

You know that the Jones family has five children, and the Smith family has three children. Of the eight children you know that there are five girls and three boys. Let be the probability that at least one of the fa milies has only girls for children. Given that m and n are relatively prime positive integers, find m+ n.

 

Problem 9

The four sets A, B, C, and D each have 400 elements. The intersection of any two of the sets has 115 elements. The intersection of any three of the sets has 53 elements. The intersection of all four sets has 28 elements. How many elements are there in the union of the four sets?

 

Problem 10

For a particular value of the angle θ we can take the product of the two complex

numbers

to get a complex number in the form a + bi where a and b are real numbers.

Find the largest value for a + b.

 

Problem 11

A dart board looks like three concentric circles with radii of 4, 6, and 8. Three darts are thrown at the board so that they stick at three random locations on the board. The probability that one dart sticks in each of the three regions of the dart board is  where m and n are relatively prime positive integers.

Find m + n.

 

Problem 12

Find the maximum possible value of as x varies over the positive real numbers.

 

Problem 13

Find the circumradius of the triangle with side lengths 104, 112, and 120.

 

Problem 14

Square ABCD has side length 1000. Squares with side length 400 are cut from each of the corners C and D as shown. m and n are relatively prime positive integers such that the centroid (the center of mass or balance point) of the resulting figure is at a point P at a distance from side AB. Find m + n.

 

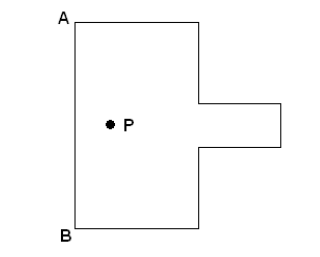
Problem 15

The alphabet in its natural order ABCDEFGHIJKLMNOPQRSTUVWXYZ is T0 . We apply a permutation to T0 to get T₁ which is JQOWIPANTZRCVMYEGSHUFDKBLX. If we apply the same permutation to T₁ , we get T₂ which is ZGYKTEJMUXSODVLIAHNFPWRQCB. We continually apply this permutation to each T_m to get T _m+1. Find the smallest positive integer n so that T_n = T₀ .

 

Problem 16

We have some identical paper squares which are black on one side of the sheet and white on the other side. We can join nine squares together to make a 3 by 3 sheet of squares by placing each of the nine squares either white side up or black side up. Two of these 3 by 3 sheets are distinguishable if neither can be made to look like the other by rotating the sheet or by turning it over. How many distinguishable 3 by 3 squares can we form?

 

Problem 17

A circle with diameter 20 has points A, B, C, D, E, and F equally spaced along its circumference. A second circle is tangent to the lines AB and AF and internally tangent to the circle. If the second circle has diameter  for integers m and n, find m + n.

 

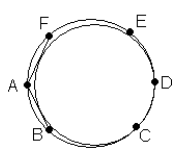
Problem 18

Let S be the graph of y=x³ , and T be the graph of . Let S* be S rotated around the origin 15 degrees clockwise, and T* be T rotated around the origin 45 degrees counterclockwise. S* and T* will intersect at a point in the first quadrant a distance from the origin where m and n are positive integers. Find m + n.

 

Problem 19

Six chairs sit in a row. Six people randomly seat themselves in the chairs. Each person randomly chooses either to set their feet on the floor, to cross their legs to the right, or to cross their legs to the left. There is only a problem if two people sitting next to each other have the person on the right crossing their legs to the left and the person on the left crossing their legs to the right. The probability that this will not happen is given by where m and n are relatively prime positive integers. Find m + n.

 

 

Problem 20

Three congruent ellipses are mutually tangent. Their major axes are parallel. Two of the ellipses are tangent at the end points of their minor axes as shown. The distance between the centers of these two ellipses is 4. The distances from those two centers to the center of the third ellipse are both 14. There are positive integers m and n so that the area between these three ellipses is Find m + n.

 

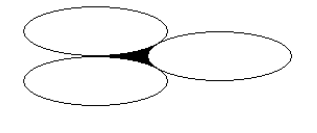
Problem 21

What is the greatest positive integer m such that

 

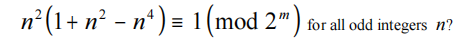
Problem 22

 

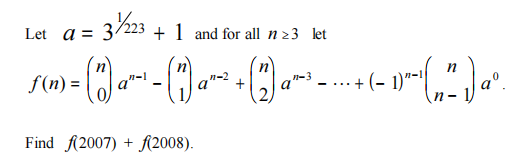
Problem 23

Two circles with radius 2 and radius 4 have a common center at P. Points A, B, and C on the larger circle are the vertices of an equilateral triangle. Point D is the intersection of the smaller circle and the line segment PB. Find the square of the area of triangle ADC.

 

Problem 24

Starting with a sequence of n 1's, you can insert plus signs to get various sums. For example, when n = 10, you can get the sum 1 + 1 + 1 + 11 + 11 + 111 = 136 and the sum 1 + 1 + 11 + 111 + 111 = 235. Find the number of values of n so that the sum of 1111 is possible.

 

Problem 25

Let x be a positive integer less than 200, and let y be obtained by writing the base 10 digits of x in reverse order. Given that x and y satisfy 11x² + 363y =7xy+6571, find x.

 

扫描下方二维码获取本年度学术活动答案及解析

还可免费领取最新年度真题及答案解析