紫色彗星数学竞赛真题（2006年高中组）

UW-Whitewater / UT-Dallas Mathematics Meet – April 2006

HIGH SCHOOL

© Copyright Titu Andreescu and Jonathan Kane

Problem 1

The sizes of the freshmen class and the sophomore class are in the ratio 5:4. The sizes of the sophomore class and the junior class are in the ratio 7:8. The sizes of the junior class and the senior class are in the ratio 9:7. If these four classes together have a total of 2158 students, how many of the students are freshmen?

 

Problem 2

At a movie theater tickets for adults cost 4 dollars more than tickets for children. One afternoon the theater sold 100 more child tickets than adult tickets for a total sales amount of 1475 dollars. How many dollars would the theater have taken in if the same tickets were sold, but the costs of the child tickets and adult tickets were reversed?

 

Problem 3

Point P lies outside a circle, and two rays are drawn from P that intersect the circle as shown. One ray intersects the circle at points A and B while the other ray intersects the circle at M and N AN and MB intersect at X. Given that ∠ AXB measures 127° and the minor arc AM measures 14°, compute the measure of the angle at P.

 

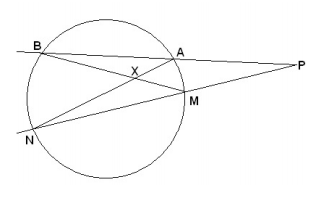
Problem 4

A rogue spaceship escapes. 54 minutes later the police leave in a spaceship in hot pursuit. If the police spaceship travels 12% faster than the rogue spaceship along the same route, how many minutes will it take for the police to catch up with the rogues?

 

Problem 5

Find the sum of all positive integers less than 2006 which are both multiples of six and one more than a multiple of seven.

 

Problem 6

The positive integers v, w, x, y, and z satisfy the equation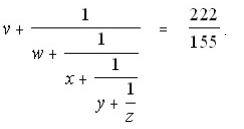

Compute 10⁴ v + 10³w + 10²x + 10¹ + 10⁰z.

 

Problem 7

Heather and Kyle need to mow a lawn and paint a room. If Heather does both jobs by herself, it will take her a total of nine hours. If Heather mows the lawn and, after she finishes, Kyle paints the room, it will take them a total of eight hours. If Kyle mows the lawn and, after he finishes, Heather paints the room, it will take them a total of seven hours. If Kyle does both jobs by himself, it will take him a total of six hours. It takes Kyle twice as long to paint the room as it does for him to mow the lawn. The number of hours it would take the two of them to complete the two tasks if they worked together to mow the lawn and then worked together to paint the room is a fraction where m and n are relatively prime positive integers. Find m + n.

 

Problem 8

Evaluate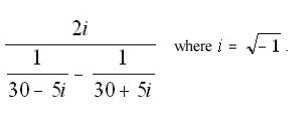

 

Problem 9

How many rectangles are there in the diagram below such that the sum of the numbers within the rectangle is a multiple of 7?

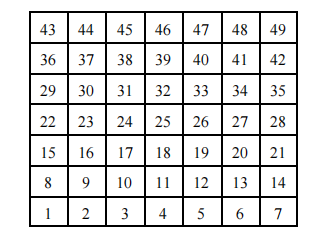
Problem 10

An equilateral triangle with side length 6 has a square of side length 6 attached to each of its edges as shown. The distance between the two farthest vertices of two squares (marked A and B in the figure) can be

written as   where m and n are positive integers. Find m + n.

 

Problem 11

Let k be the product of every third positive integer from 2 to 2006, that is,. Find the number of zeros there are at the right end of the decimal representation for k

 

Problem 12

We draw a triangle inside of a circle with one vertex at the center of the circle and the other two vertices on the circumference of the circle. The angle at the center of the circle measures 75 degrees. We draw a second triangle, congruent to the first, also with one vertex at the center of the circle and the other vertices on the circumference of the circle rotated 75 degrees clockwise from the first triangle so that it shares a side with the first triangle. We draw a third, fourth, and fifth such triangle each rotated 75 degrees clockwise from the previous triangle. The base of the fifth triangle will intersect the base of the first triangle. What is the degree measure of the obtuse angle formed by the intersection?

 

Problem 13

12 students need to form five study groups. They will form three study groups with 2 students each and two study groups with 3 students each. In how many ways can these groups be formed?

 

Problem 14

Consider all ordered pairs (m, n) of positive integers satisfying 59 m – 68 n = mn. Find the sum of all the possible values of n in these ordered pairs.

 

Problem 15

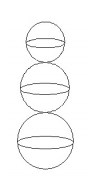
A snowman is built on a level plane by placing a ball radius 6 on top of a ball radius 8 on top of a ball radius 10 as shown. If the average height above the plane of a point in the snowman is where m and n are relatively prime positive integers, find m + n.

Problem 16

f(x) and g(x) are linear functions such that for all x . If f(0) = 4 and g(5) = 17, compute f (2006).

 

Problem 17

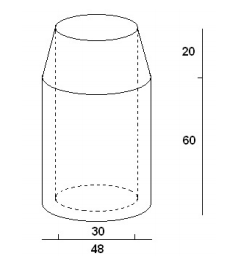
A concrete sewer pipe fitting is shaped like a cylinder with diameter 48 with a cone on top. A cylindrical hole of diameter 30 is bored all the way through the center of the fitting as shown. The cylindrical portion has height 60 while the conical top portion has height 20. Find N such that the volume of the concrete is NB .

Problem 18

In how many ways can 100 be written as the sum of three positive integers x, y, and z satisfying x < y < z?

 

Problem 19

There is a very popular race course where runners frequently go for a daily run. Assume that all runners randomly select a start time, a starting position on the course, and a direction to run. Also assume that all runners make exactly one complete circuit of the race course, all runners run at the same speed, and all runners complete the circuit in one hour. Suppose that one afternoon you go for a run on this race course, and you count 300 runners which you pass going in the opposite direction, although some of those runners you count twice since you pass them twice. What is the expected value of the number of different runners that you pass not counting duplicates?

 

Problem 20

Find the sum of all the positive integers which have at most three not necessarily distinct prime factors where the primes come from the set {2, 3, 5, 7}.

 

Problem 21

In triangle ABC, AB = 52, BC = 56, CA = 60. Let D be the foot of the altitude from A and E be the intersection of the internal angle bisector of pBAC with BC. Find DE.

 

Problem 22

Problem 23

We have two positive integers both less than 1000. The arithmetic mean and the geometric mean of these numbers are consecutive odd integers. Find the maximum possible value of the difference of the two integers.

 

Problem 24

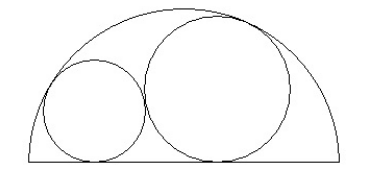
A semicircle with diameter length 16 contains a circle radius 3 tangent both to the inside of the semicircle and its diameter as shown. A second larger circle is tangent to the inside of the semicircle, the outside of the circle, and the diameter of the semicircle. The diameter of the second circle can be written as where m, n, and k are positive integers and m and n  have no factors in common. Find m + n + k.

Problem 25

Let x and y be two real numbers such that Find tan²x + 2 tan²y.

 

扫描下方二维码获取本年度学术活动答案及解析

还可免费领取最新年度真题及答案解析