- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
紫色彗星数学竞赛真题(2005年高中组)
UW-Whitewater / UT-Dallas Mathematics Meet – April 14, 2005
HIGH SCHOOL
© Copyright Titu Andreescu and Jonathan Kane
Problem 1
The cost of producing each item is inversely proportional to the square root of the number of items produced. The cost of producing ten items is $2100. If items sell for $30 each, how many items need to be sold so that the producers break even?
Problem 2
We glue together 990 one inch cubes into a 9 by 10 by 11 inch rectangular solid. Then we paint the outside of the solid. How many of the original 990 cubes have just one of their sides painted?
Problem 3
Four rectangular strips each measuring 4 by 16 inches are laid out with two vertical strips crossing two horizontal strips forming a single polygon which looks like a tic-tack-toe pattern. What is the perimeter of this polygon?
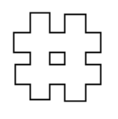
Problem 4
A palindrome is a number that reads the same forwards and backwards such as 3773 or 42924. What is the smallest 9 digit palindrome which is a multiple of 3 and has at least two digits which are 5's and two digits which are 7's?
Problem 5
In January Jeff’s investment went up by three quarters. In February it went down by one quarter. In March it went up by one third. In April it went down by one fifth. In May it went up by one seventh. In June Jeff’s investment fell by![]() where m and n are relatively prime positive integers. If Jeff’s investment was worth the same amount at the end of June as it had been at the beginning of January, find m + n.
where m and n are relatively prime positive integers. If Jeff’s investment was worth the same amount at the end of June as it had been at the beginning of January, find m + n.
Problem 6
ABCDE is a regular pentagon. What is the degree measure of the acute angle at the intersection of line segments AC and BD?
Problem 7
The graph of the equation y=5x+24 intersects the graph of the equation at two points. The two points are a distance ![]() apart. Find N.
apart. Find N.
Problem 8
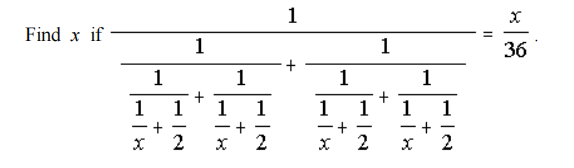
Problem 9
Let T be a 30-60-90 triangle with hypotenuse of length 20. Three circles, each externally tangent to the other two, have centers at the three vertices of T. The area of the union of the circles intersected with T is ![]() for rational numbers m and n. Find m + n.
for rational numbers m and n. Find m + n.
Problem 10
A jar contains 2 yellow candies, 4 red candies, and 6 blue candies. Candies are randomly drawn out of the jar one-by-one and eaten. The probability that the 2 yellow candies will be eaten before any of the red candies are eaten is given by the fraction ![]() where m and n are relatively prime positive integers. Find m + n.
where m and n are relatively prime positive integers. Find m + n.
Problem 11
The straight river is one and a half kilometers wide and has a current of 8 kilometers per hour. A boat capable of traveling 10 kilometers per hour in still water, sets out across the water. How many minutes will it take the boat to reach a point directly across from where it started?
Problem 12
Find the number of nonnegative integers n for which (n2 -3n+1)2 is a prime number.
Problem 13
The work team was working at a rate fast enough to process 1250 items in ten hours. But after working for six hours, the team was given an additional 165 items to process. By what percent does the team need to increase its rate so that it can still complete its work within the ten hours?
Problem 14
Four mathletes and two coaches sit at a circular table. How many distinct arrangements are there of these six people if the two coaches sit opposite each other?
Problem 15
And it came to pass that Jeb owned over a thousand chickens. So Jeb counted his chickens. And Jeb reported the count to Hannah. And Hannah reported the count to Joshua. And Joshua reported the count to Caleb. And Caleb reported the count to Rachel. But as fate would have it, Jeb had over-counted his chickens by nine chickens. Then Hannah interchanged the last two digits of the count before reporting it to Joshua. And Joshua interchanged the first and the third digits of the number reported to him before reporting it to Caleb. Then Caleb doubled the number reported to him before reporting it to Rachel. Now it so happens that the count reported to Rachel was the correct number of chickens that Jeb owned. How many chickens was that?
Problem 16
A tailor met a tortoise sitting under a tree. When the tortoise was the tailor’s age, the tailor was only a quarter of his current age. When the tree was the tortoise’s age, the tortoise was only a seventh of its current age. If the sum of their ages is now 264, how old is the tortoise?
Problem 17
Functions f and g are defined so that f(1)=4,g(1)=9,and for each integer n≥1,f(n+1)=2f(n)+3g(n)+2n and g(n+1)=2g(n)+3f(n)+5. Find f(2005)-g(2005).
Problem 18
The side lengths of a trapezoid are ![]() and
and![]() . Its area is the ratio of two relatively prime positive integers, m and n. Find m + n.
. Its area is the ratio of two relatively prime positive integers, m and n. Find m + n.
Problem 19
Let x and y be integers satisfying both x2-16x+3y=20 and y2+4y-x=-12. Find x + y.
Problem 20
The summation 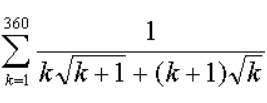 is the ratio of two relatively prime positive integers m and n. Find m + n.
is the ratio of two relatively prime positive integers m and n. Find m + n.
Problem 21
In the diagram below angle CAB, angle CBD, and angle CDE are all right angles with side lengths AC = 3, BC = 5, BD = 12, and DE = 84. The distance from point E to the line AB can be expressed as the ratio of two relatively prime positive integers, m and n. Find m + n.
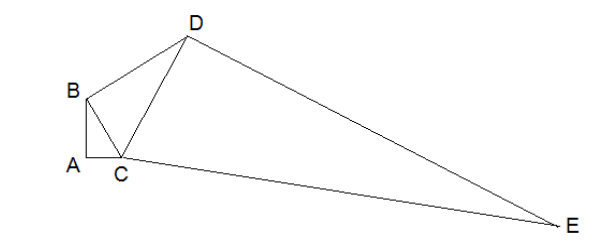
Problem 22
Let dk be the greatest odd divisor of k for k = 1, 2, 3, ... Find ![]()
Problem 23
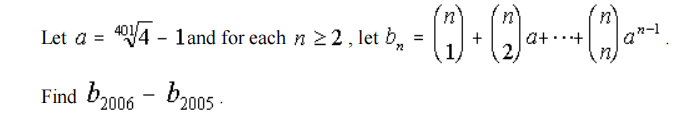
Problem 24
Triangle ABC has area 240. Points X, Y, Z lie on sides AB, BC, and CA, respectively. Given that  , find the area of triangle XYZ.
, find the area of triangle XYZ.
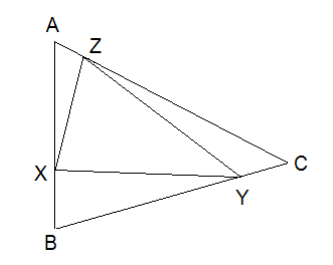
Problem 25
Find the number of quadruples (a,b,c,d) of integers which satisfy both ![]() and 2(a+b+c+d)=ab+cd+(a+b)(c+d)+1.
and 2(a+b+c+d)=ab+cd+(a+b)(c+d)+1.
扫描下方二维码获取本年度学术活动答案及解析
还可免费领取最新年度真题及答案解析


早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








