紫色彗星数学竞赛真题（2012年初中组）

紫色彗星数学学术活动真题（2011年初中组）

PURPLE COMET MATH MEET April 2012
MIDDLE SCHOOL - PROBLEMS
Copyright© Titu Andreescu and Jonathan Kane

Problem 1
Evaluate 5⁴ − 4³ − 3² − 2¹ − 1⁰.
Problem 2

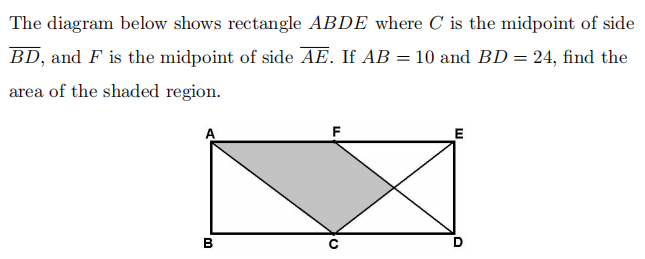
Problem 3
While Peter was driving from home to work, he noticed that after driving 21 miles, the distance he had left to drive was 30 percent of the total distance from home to work. How many miles was his complete trip from home to work?
Problem 4
How many two-digit positive integers contain at least one digit equal to 5?
Problem 5
Meredith drives 5 miles to the northeast, then 15 miles to the southeast, then 25 miles to the southwest, then 35 miles to the northwest, and finally 20 miles to the northeast. How many miles is Meredith from where she started?
Problem 6
Volume A equals one fourth of the sum of the volumes B and C, while volume B equals one sixth of the sum of the volumes A and C. There are relatively prime positive integers m and n so that the ratio of volume C to the sum of the other two volumes is . Find m + n.
Problem 7
A snail crawls 2 centimeters in 4 minutes. At that rate, how many centimeters can the snail crawl in 85 minutes?
Problem 8
Seven boys and three girls are playing basketball. In how many different ways can they make two teams of five players so that both teams have at least one girl?
Problem 9
Points E and F lie inside rectangle ABCD with AE = DE = BF = CF = EF. If AB = 11 and BC = 8, find the area of the quadrilateral AEF B.
Problem 10
Find the least positive multiple of 999 that does not have 9 as a digit.
Problem 11
For some integers a and b the function f(x) = ax + b has the properties that f (f(0)) = 0 and f (f (f(4))) = 9. Find f (f (f (f(10)))).
Problem 12

Problem 13
Find the least positive integer N which is both a multiple of 19 and whose digits add to 23.
Problem 14
At the 4 PM show, all the seats in the theater were taken, and 65 percent of the audience was children. At the 6 PM show, again, all the seats were taken, but this time only 50 percent of the audience was children. Of all the people who attended either of these shows, 57 percent were children although there were 12 adults and 28 children who attended both shows. How many people does the theater seat?
Problem 15
The top and bottom of a rectangular tank each has area 48 square inches. The four vertical sides of the tank have a total area of 96 square inches. The longest diagonal of the tank is 13 inches. Find the sum of the height, the width, and the length of this tank in inches.
Problem 16
The following sequence lists all the positive rational numbers that do not exceed by first listing the fraction with denominator 2, followed by the one with denominator 3, followed by the two fractions with denominator 4 in increasing order, and so forth so that the sequence is

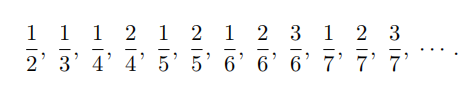
Let m and n be relatively prime positive integers so that the 2012th fraction in the list is equal to . Find m + n.
Problem 17

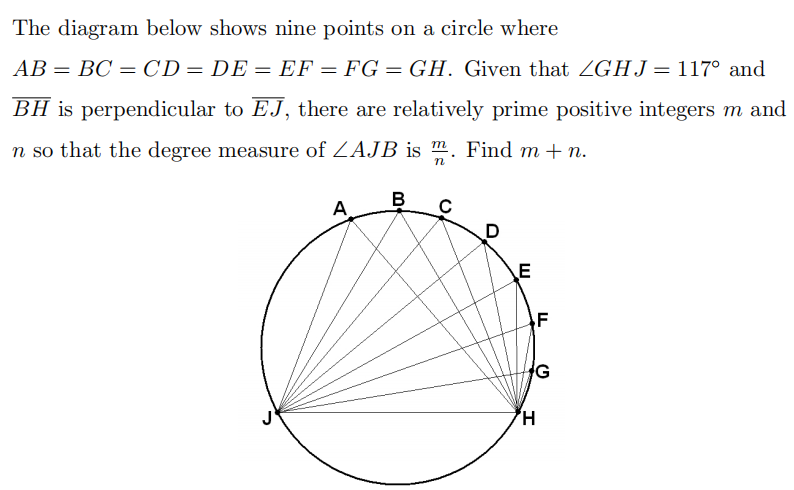
Problem 18
Find the smallest positive integer whose remainder when divided by 5 is 3, when divided by 7 is 5, and when divided by 9 is 1.
Problem 19
A teacher suggests four possible books for students to read. Each of six students selects one of the four books. How many ways can these selections be made if each of the books is read by at least one student?
Problem 20
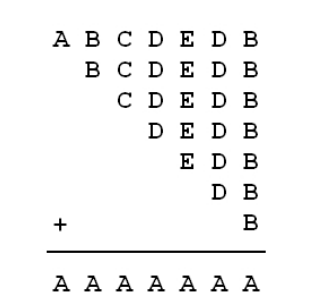
In the following addition, different letters represent different non-zero digits.What is the 5-digit number ABCDE?

紫色彗星数学学术活动真题（2012年初中组）解析以及答案，最新年份真题，扫码免费领取