紫色彗星数学竞赛真题（2004年高中组）

Spring 2004 UW-Whitewater High School

Mathematics Meet

Titu Andreescu and Jonathan Kane∗

March 18, 2004

Instructions

Teams may fifill in answers to the questions over the next 90 minutes. At any time contestants can click the SUBMIT button to submit their team’s entry. Answers may be submitted multiple times by the same team, but only the last set of answers received before the contest ends will be accepted and graded. Contestants are allowed to work on these problems as a team. No help may be provided by persons not on their team. There is no penalty for guessing. (See offiffifficial rules for complete contest rules.)

 

Problem 1

How many difffferent positive integers divide 10! ?

 

Problem 2

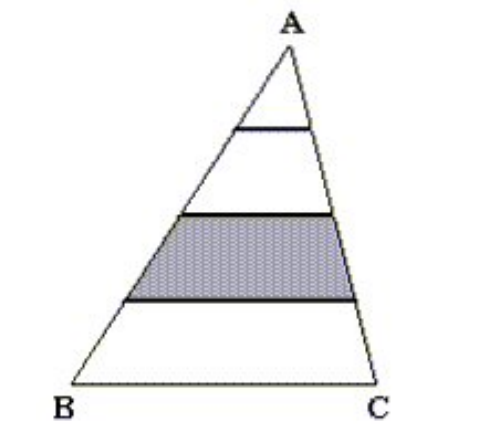
In triangle ABC, three lines are drawn parallel to side BC dividing the altitude of the triangle into four equal parts. If the area of the second largest part is 35, what is the area of the whole triangle ABC ?

∗Department of Mathematical and Computer Sciences, University of Wisconsin, Whitewater, Wis consin 53190

 

Problem 3

How many real numbers are roots of the polynomial

x⁹ − 37x⁸ − 2x⁷ + 74x⁶ + x⁴− 37x³ − 2x² + 74x?

Problem 4

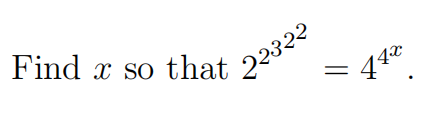
Problem 5

The number 2.5081081081081... can be written as m/n where m and n are natural numbers with no common factors. Find m + n.

 

Problem 6

Evaluate the product

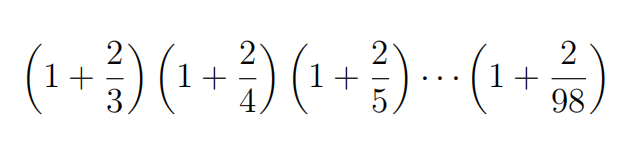
Problem 7

How many positive integers less that 200 are relatively prime to either 15 or 24?

 

Problem 8

One rainy afternoon you write the number 1 once, the number 2 twice, the number 3 three times, and so forth until you have written the number 99 ninety-nine times. What is the 2005th digit that you write?

 

Problem 9

Let M and m be the largest and the smallest values of x, respectively, which satisfy 4x(x − 5) ≤ 375. Find M − m.

 

Problem 10

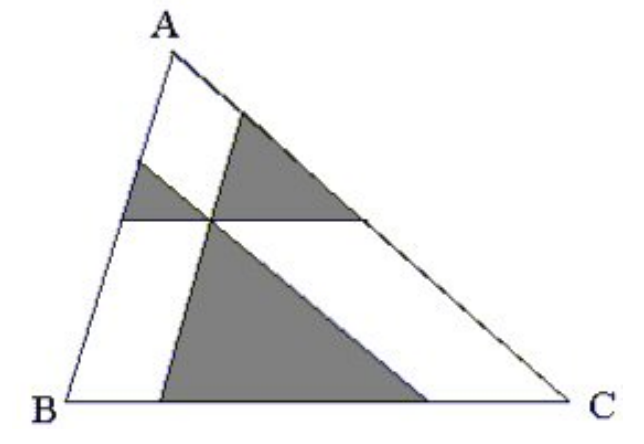
Three lines are drawn parallel to each of the three sides of triangle ABC so that the three lines intersect in the interior of ABC. The resulting three smaller triangles have areas 1, 4, and 9. Find the area of triangle ABC.

Problem 11

How far is it from the point (9, 17) to its reflflection across the line 3x + 4y = 15?

 

Problem 12

The diagram shows a circle with radius 24 which contains two circles with radius 12 tangent to each other and the larger circle. The smallest circle is tangent to the three other circles. What is the radius of the smallest circle?

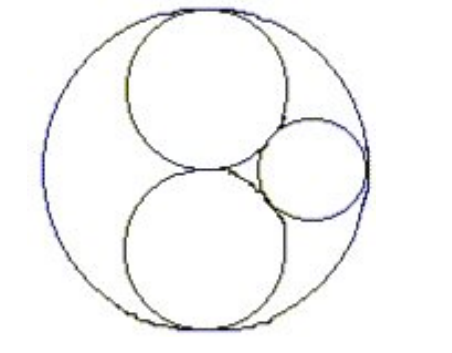
Problem 13
A cubic block with dimensions n by n by n is made up of a collection of 1 by 1 by 1 unit cubes. What is the smallest value of n so that if the outer two layers of unit cubes are removed from the block, more than half the original unit cubes will still remain?

 

Problem 14

Two circles have radii 15 and 95. If the two external tangents to the circles intersect at 60 degrees, how far apart are the centers of the circles?

 

Problem 15

Jerry purchased some stock for $14,400 at the same time that Susan purchased a bond for $6,250. Jerry’s investment went up 20 percent the fifirst year, fell 10 percent the second year, and rose another 20 percent the third year. Susan’s investment grew at a constant rate of compound interest for three years. If both investments are worth the same after three years, what was the annual percentage increase of Susan’s investment?

 

Problem 16

Find the total length of the set of real numbers satisfying

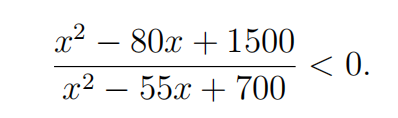
Problem 17

We want to paint some identically-sized cubes so that each face of each cube is painted a solid color and each cube is painted with six difffferent colors. If we have seven difffferent colors to choose from, how many distinguishable cubes can we produce?

 

Problem 18

As x ranges over the interval (0, ∞), the function

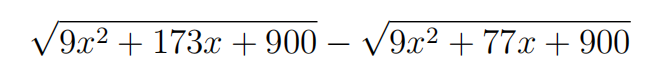
ranges over the interval (0, M). Find M.

 

Problem 19

There are three bags. One bag contains three green candies and one red candy. One bag contains two green candies and two red candies. One bag contains one green candy and three red candies. A child randomly selects one of the bags, randomly chooses a fifirst candy from that bag, and eats the candy. If the fifirst candy had been green, the child randomly chooses one of the other two bags and randomly selects a second candy from that bag. If the fifirst candy had been red, the child randomly selects a second candy from the same bag as the fifirst candy. If the probability that the second candy is green is given by the fraction m/n in lowest terms, fifind m + n.

 

Problem 20

A 70 foot pole stands vertically in a plane supported by three 490 foot wires, all attached to the top of the pole, pulled taut, and anchored to three equally spaced points in the plane. How many feet apart are any two of those anchor points?

Problem 21

Defifine a_k = (k² + 1)k! and b_k = a₁ + a₂ + a₃ + · · · + a_k. Let

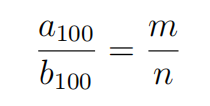
where m and n are relatively prime natural numbers. Find n − m.

 

Problem 22

How many non-overlapping 2 by 2 squares will fifit into a circle with radius 8?

 

Problem 23

Let a and b be real numbers satisfying

a⁴ + 8b = 4(a³ − 1) − 16√3

and

b⁴ + 8a = 4(b³ − 1) + 16√3.

Find a⁴ + b⁴.

 

Problem 24

The determinant

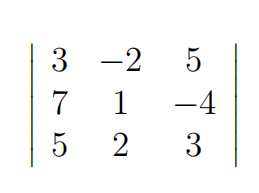
has the same value as the determinant

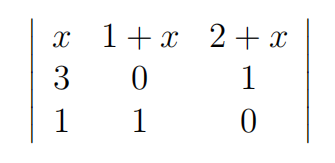
Find x.

 

Problem 25

In the addition problem

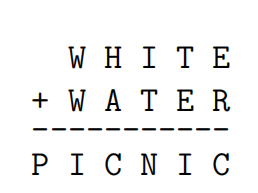
each distinct letter represents a difffferent digit. Find the number represented by the answer PICNIC.

 

扫描下方二维码获取本年度学术活动答案及解析

还可免费领取最新年度真题及答案解析