紫色彗星数学竞赛真题（2011年初中组）

PURPLE COMET MATH MEET April 2011
MIDDLE SCHOOL - PROBLEMS
Copyright ©Titu Andreescu and Jonathan Kane

Problem 1
There are relatively prime positive integers m and n so that

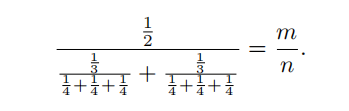
Find m + 2n.

Problem 2
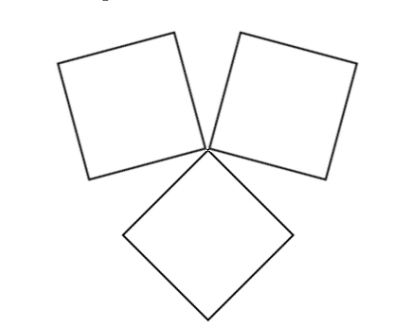
The diagram below shows a 12-sided figure made up of three congruent squares. The figure has total perimeter 60. Find its area.

Problem 3
Find the sum of all two-digit integers which are both prime and are 1 more than a multiple of 10.

Problem 4
Jerry buys a bottle of 150 pills. Using a standard 12 hour clock, he sees that the clock reads exactly 12 when he takes the first pill. If he takes one pill every five hours, what hour will the clock read when he takes the last pill in the bottle?

Problem 5

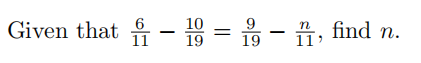
Problem 6

The following addition problem is not correct if the numbers are interpreted as base 10 numbers. In what number base is the problem correct?

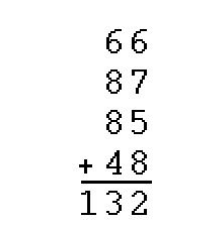
Problem 7

Problem 8
A square measuring 15 by 15 is partitioned into five rows of five congruent squares as shown below. The small squares are alternately colored black and white as shown. Find the total area of the part colored black.

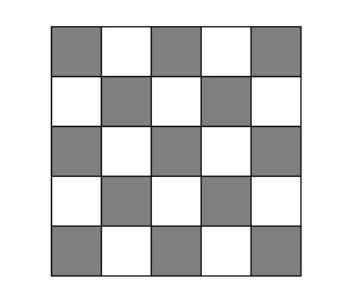
Problem 9
A jar contains one quarter red jelly beans and three quarters blue jelly beans. If Chris removes three quarters of the red jelly beans and one quarter of the blue jelly beans, what percent of the jelly beans remaining in the jar will be red?

Problem 10

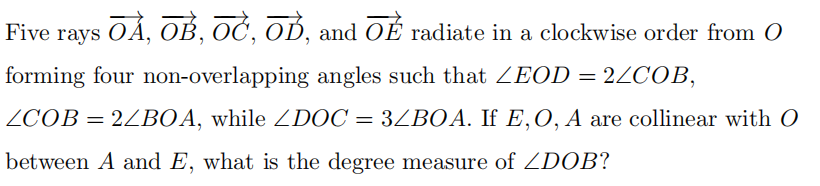
Problem 11
How many numbers are there that appear both in the arithmetic sequence 10, 16, 22, 28, ... 1000 and the arithmetic sequence 10, 21, 32, 43, ..., 1000?

Problem 12
When Troy writes his digits, his 0, 1, and 8 look the same right-side-up and upside-down as seen in the figure below. His 6 and 9 look like upside-down images of each other. None of his other digits look like digits when they are inverted. How many different five-digit numbers (which do not begin with the digit zero) can Troy write which read the same right-side-up and upside-down?

Problem 13
The diagram shows two equilateral triangles with side length 4 mounted on two adjacent sides of a square also with side length 4. The distance between the two vertices marked A and B can be written as √m + √n for two positive integers m and n. Find m + n.

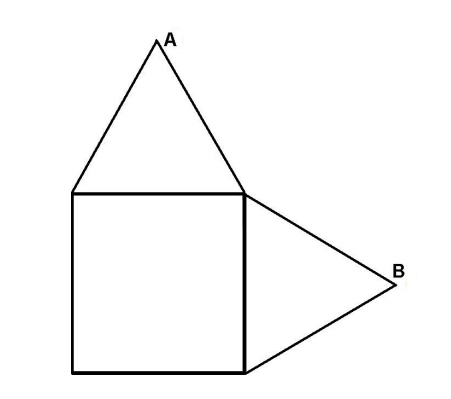
Problem 14
The five-digit number 12110 is divisible by the sum of its digits 1 + 2 + 1 + 1 + 0 = 5. Find the greatest five-digit number which is divisible by the sum of its digits.

Problem 15

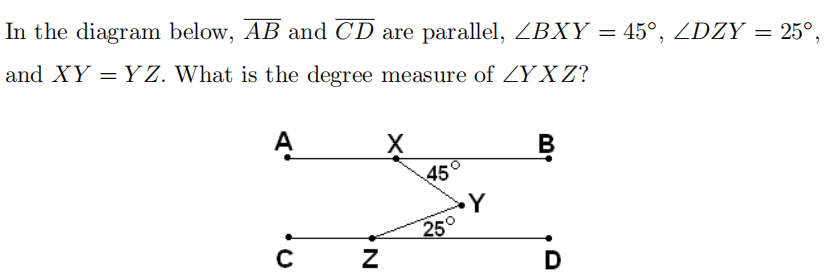
Problem 16

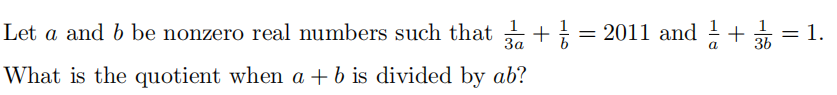
Problem 17
Find the number of ordered quadruples (a, b, c, d) where each of a, b, c, and d are (not necessarily distinct) elements of {1, 2, 3, 4, 5, 6, 7} and 3abc + 4abd + 5bcd is even. For example, (2, 2, 5, 1) and (3, 1, 4, 6) satisfy the conditions.

Problem 18
Find the positive integer n so that n² is the perfect square closest to 8 + 16 + 24 + · · · + 8040.

 

Problem 19
How many ordered pairs of sets (A, B) have the properties:
1. A ⊆ {1, 2, 3, 4, 5, 6}
2. B ⊆ {2, 3, 4, 5, 6, 7, 8}
3. A ∩ B has exactly 3 elements.

Problem 20
Let V be the set of vertices of a regular 25 sided polygon with center at point C. How many triangles have vertices in V and contain the point C in the interior of the triangle?

紫色彗星数学学术活动真题（2011年初中组）解析以及答案，最新年份真题，扫码免费领取