紫色彗星数学竞赛真题（2003年高中组）

2003 UW-Whitewater High School

Mathematics Meet

Titu Andreescu and Jonathan Kane∗

December 11, 2003

Instructions

Teams may fifill in answers to the questions over the next 90 minutes. At any time contestants can click the SUBMIT button to submit their team’s entry. Answers may be submitted multiple times by the same team, but only the last set of answers received before the contest ends will be accepted and graded. Contestants are allowed to work on these problems as a team. No help may be provided by persons not on their team. There is no penalty for guessing. (See offiffifficial rules for complete contest rules.)

 

Problem 1

In eight years Henry will be three times the age that Sally was last year.

Twenty fifive years ago their ages added to 83. How old is Henry now?

 

Problem 2

What is the smallest number that could be the date of the fifirst Saturday after the second Monday following the second Thursday of a month?

∗Department of Mathematical and Computer Sciences, University of Wisconsin, White water, Wisconsin 53190

 

Problem 3

What is the largest integer whose prime factors add to 14?

 

Problem 4

The lengths of the diagonals of a rhombus are, in inches, two consecutive integers. The area of the rhombus is 210 sq. in. Find its perimeter, in inches.

 

Problem 5

 

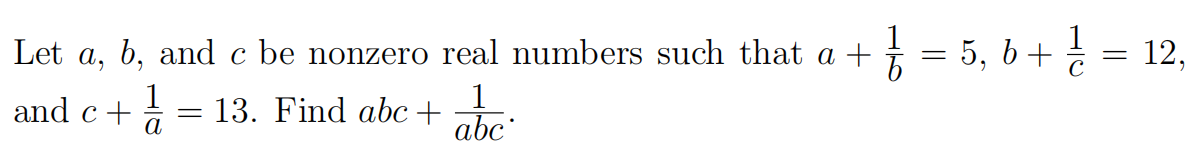
Problem 6

Evaluate:

Problem 7

Find the smallest n such that every subset of {1, 2, 3, . . . , 2004} with n elements contains at least two elements that are relatively prime.

 

Problem 8

Let ABCDEF GHIJKL be a regular dodecagon. Find

 

Problem 9

 

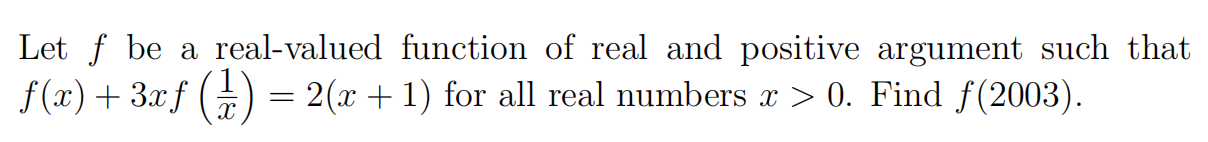
Problem 10

How many gallons of a solution which is 15% alcohol do we have to mix with a solution that is 35% alcohol to make 250 gallons of a soluition that is 21% alcohol?

 

Problem 11

If

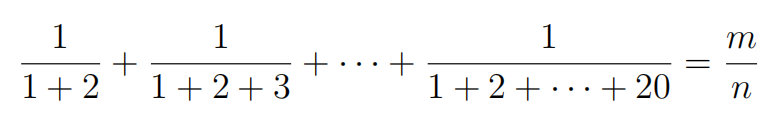
where m and n are positive integrs with no common divisor, fifind m + n.

Problem 12

How many triangles appear in the diagram below?

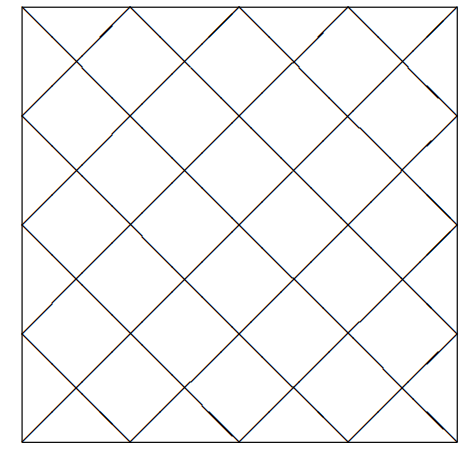
Problem 13

Let P(x) be a polynomial such that, when divided by x − 2, the remainder is 3 and, when divided by x − 3, the remainder is 2. If, when divided by (x − 2)(x − 3), the remainder is ax + b, fifind a² + b².

 

Problem 14

Let a, b, c be real numbers such that a² − 2 = 3b − c, b² + 4 = 3 + a, and c² + 4 = 3a − b. Find a⁴ + b⁴ + c⁴.

 

Problem 15

Let r be a real number such that

Problem 16

Find the largest real number x such that

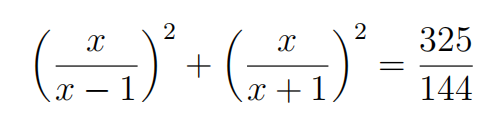
Problem 17

Given that 3 sin x + 4 cos x = 5, where x is in (0,  ), fifind 2 sin x + cos x + 4 tan x.

 

Problem 18

A circle radius 320 is tangent to the inside of a circle radius 1000. The smaller circle is tangent to a diameter of the larger circle at a point P. How far is the point P from the outside of the larger circle?

 

Problem 19

Let x1 and x2 be the roots of the equation x2 + 3x + 1 = 0. Compute

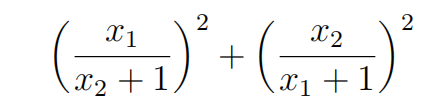
Problem 20

In how many ways can we form three teams of four players each from a group of 12 participants?

 

Problem 21

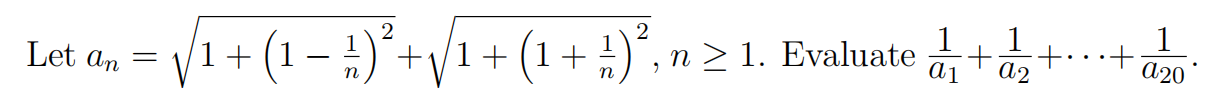
Problem 22

In triangle ABC, maxand + 1, where R  is the radius of the circumcircle and r  is the radius of the incircle. Find in degrees.

 

Problem 23

For each positive integer m and n defifine function f(m, n) by f(1, 1) = 1, f(m + 1, n) = f(m, n) + m and f(m, n + 1) = f(m, n) all the values of p such that f(p, q) = 2004 for some q.

 

Problem 24

In triangle ABC, 6 A = 30◦ and AB = AC = 16in. Let D lie on segment BC such that  Let E and F be the orthogonal projections of D onto AB and AC, respectively. Find DE + DF in inches.

 

Problem 25

Given that (1 + tan 1◦ )(1 + tan 2◦). . .(1 + tan 45◦ ) = 2n , fifind n.

 

扫描下方二维码获取本年度学术活动答案及解析

还可免费领取最新年度真题及答案解析