紫色彗星数学竞赛真题（2010年初中组）

PURPLE COMET MATH MEET April 2010
MIDDLE SCHOOL - PROBLEMS
© Copyright Titu Andreescu and Jonathan Kane

Problem 1
If 125 + n + 135 + 2n + 145 = 900, find n.

Problem 2
Three boxes each contain four bags. Each bag contains five marbles. How many marbles are there altogether in the three boxes?

Problem 3

Problem 4
The grid below contains five rows with six points in each row. Points that are adjacent either horizontally or vertically are a distance one apart. Find the area of the pentagon shown.

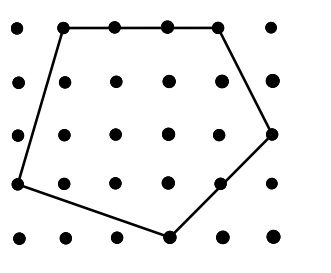
Problem 5
Find the least positive integer k so that k + 25973 is a palindrome (a number which reads the same forward and backwards)

Problem 6
Find the sum of the prime factors of 777.

Problem 7
x and y are positive real numbers where x is p percent of y, and y is 4p percent of x. What is p?

Problem 8
There are exactly two four-digit numbers that are multiples of three where their first digit is double their second digit, their third digit is three more than their fourth digit, and their second digit is 2 less than their fourth digit. Find the difference of these two numbers.

【福利插播】

紫色彗星数学学术活动真题（2010年初中组）解析以及答案，最新年份真题，扫码免费领取：

Problem 9
What percent of the numbers 1, 2, 3, ... 1000 are divisible by exactly one of the numbers 4 and 5?

Problem 10

Problem 11
There are two rows of seats with three side-by-side seats in each row. Two little boys, two little girls, and two adults sit in the six seats so that neither little boy sits to the side of either little girl. In how many different ways can these six people be seated?

Problem 12
The diagram below shows twelve 30-60-90 triangles placed in a circle so that the hypotenuse of each triangle coincides with the longer leg of the next triangle. The fourth and last triangle in this diagram are shaded. The ratio of the perimeters of these two triangles can be written as where m and n are relatively prime positive integers. Find m + n.

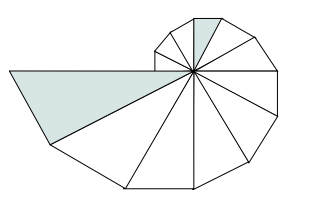
Problem 13
Find the number of sets A that satisfy the three conditions:
• A is a set of two positive integers
• each of the numbers in A is at least 22 percent the size of the other number
• A contains the number 30.

Problem 14

Problem 15
In the number arrangement
1
2      3
4      5       6
7      8       9       10
11   12     13     14      15
...
what is the number that will appear directly below the number 2010?

Problem 16
Half the volume of a 12 foot high cone-shaped pile is grade A ore while the other half is grade B ore. The pile is worth $62. One-third of the volume of a similarly shaped 18 foot pile is grade A ore while the other two-thirds is grade B ore. The second pile is worth $162. Two-thirds of the volume of a similarly shaped 24 foot pile is grade A ore while the other one-third is grade B ore. What is the value in dollars ($) of the 24 foot pile?

Problem 17
The diagram below shows a triangle divided into sections by three horizontal lines which divide the altitude of the triangle into four equal parts, and three lines connecting the top vertex with points that divide the opposite side into four equal parts. If the shaded region has area 100, find the area of the entire triangle.

Problem 18
How many three-digit positive integers contain both even and odd digits?

Problem 19
Square A is adjacent to square B which is adjacent to square C. The three squares all have their bottom sides along a common horizontal line as shown. The upper left vertices of the three squares are collinear. If square A has area 24, and square B has area 36, find the area of square C.

Problem 20