2019-2020 BPHO英国物理奥赛第一轮第一部分真题及解析

BPhO Round 1

Section 1

15th November 2019

This question paper must not be taken out of the exam room

Instructions Time: 1 hour 20 minutes for this section.

Questions: Students may attempt any parts of Section 1, but are not expected to complete all parts.

Working: Working, calculations, explanations and diagrams, properly laid out, must be shown for full credit. The fifinal answer alone is not suffificient. Writing must be clear.

Marks: A maximum of 50 marks can be awarded for Section 1. There is a total of 88 marks allocated to the problems of Question 1 which makes up the whole of Section 1.

Instructions: You are allowed any standard exam board data/formula sheet.

Calculators: Any standard calculator may be used, but calculators cannot be programmable and must not have symbolic algebra capability.

Solutions: Answers and calculations are to be written on loose paper or in examination booklets. Graph paper and formula sheets should also be made available. Students should ensure that their name and their

school/college are clearly written on each and every answer sheet. Number each question clearly and number the pages.

Sitting the paper: There are two options for sitting BPhO Round 1: a. Section 1 and Section 2 may be sat in one session of 2 hours 40 minutes plus 5 minutes reading time (for Section 2 only).

Section 1 should be collected in after 1 hour 20 minutes and then Section 2 given out. b. Section 1 and Section 2 may be sat in two sessions on separate occasions, with 1 hour 20 minutes plus 5 minutes reading time allocated for Section 2. If the paper is taken in two sessions on separate occasions, Section 1 must be collected in after the fifirst session and Section 2 handed out at the beginning of the second session.

Question 1 a) A golf ball is struck and begins to move at an initial velocity of 60 m s−1 at an angle 40◦ above the horizontal. Determine at time t = 3 s after the strike
(i) the velocity of the ball, and
(ii) the position of the ball relative to the origin.

b) A drone flflies horizontally. The displacement of the drone is given by where and are unit vectors to the East and North respectively. Determine at t = 2 s:
(i) the speed of the drone,
(ii) its bearing in degrees,
(iii) its acceleration.
Note: all bearings are measured clockwise from North.

c) Estimate the mass of a piece of paper the size of a pinhead (the blunt end of a sewing pin). Show your calculation.

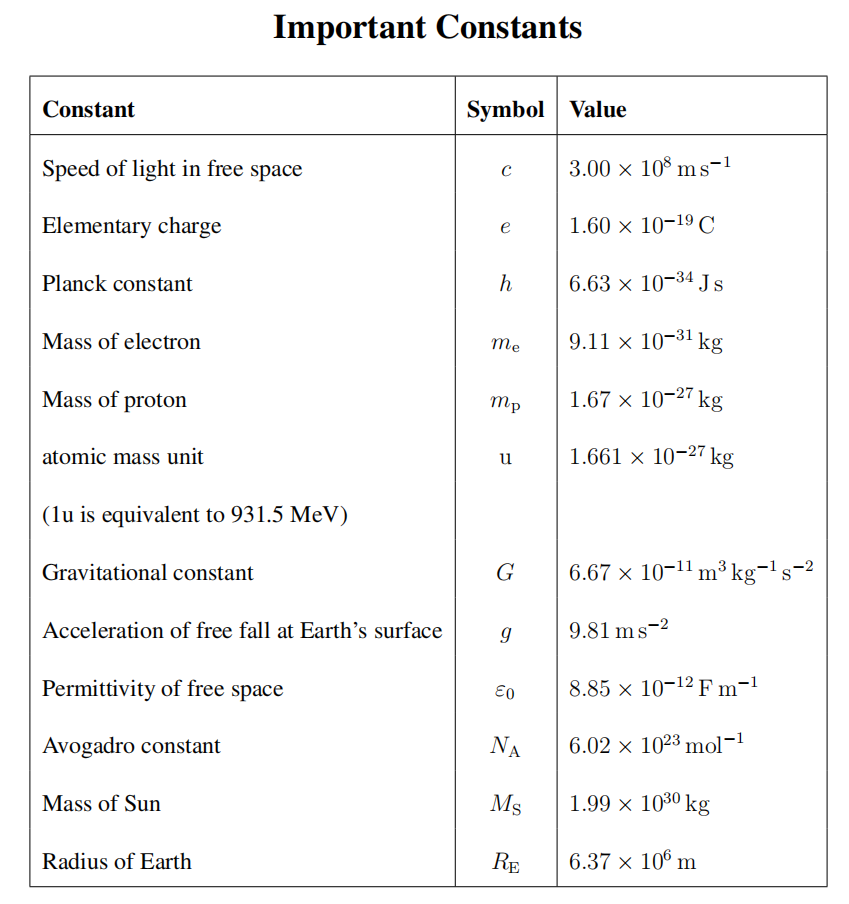
d) The speed of surface waves of wavelength λ on a liquid of density ρ is given by 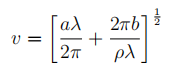where a and b are constants. Determine the units of a and b.

e) Figure 1 shows the cross section of a high voltage overhead electrical transmission cable.
The central strand is of steel and the six outer strands are of aluminium. The resistivity of steel is 2.0 × 10−7 Ω m, and that of aluminium 3.2 × 10−8 Ωm. The cross-sectional area of each strand is 5.0 × 10−4 m2 . The steel is present to give mechanical strength to the cable and only reduces the resistance of a length ` of cable by 1.4 × 10−4 Ω when it is included. Calculate the length of the cable. 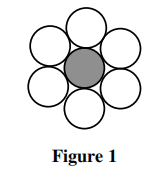f) Platinum (symbol Pt) and potassium (symbol K) have densities of 21.5 g cm ^-3 and 0.89 g cm ^-3 respectively. How many cubic centimetres (cm3 ) of platinum could be attached to 10.0 cm ³ of potassium before the combination sinks in mercury of density 13.6 g cm ^-3 ? Ignore any chemical reactions.

g) One kilogram of ice at 0 ◦C is placed in a thermally insulated bucket of volume 5 Water at 15 ◦C is added until the bucket is completely fifilled. Calculate the temperature of the water when half of the ice has melted.
1 litre = 1000 cm ³ Latent heat of fusion of ice, Lice = 3.34 × 105 J kg ^-1 Specifific thermal capacity of water, cice = 4180 J kg ^-1 k ^-1 Densities: ρice = 920 kg m−3 and ρwater = 1000 kg m ^-3
h) This question concerns three vessels at sea: a ferry (F), a container ship (C), and a pilot boat (P). The ferry is sailing on a bearing of 090◦ at 5 ms ^-1 . Relative to the ferry, the container ship is sailing on a bearing of 160◦ . The pilot boat is sailing on a bearing of 270◦ at 7.5 ms ^-1 , and the pilot boat observes the container ship moving on a bearing of 120◦.
Determine the speed and direction of the container ship relative to the water.
Note: all bearings are measured clockwise from North.

i) A car accelerates from a standing start. If the mass of the car is m, and the car is driven at constant driving power P, fifind an expression for the velocity of the car v as a function of distance travelled from a standing start, x. Ignore resistive effects and ineffificiencies in power transmission.

j) An experiment is proposed which involves submerging a ball of mass m and radius r to a depth of d 》r in a swimming pool. The ball is then released, and emerges from the water and rises to a height h 》r above the surface. The quantities d and h are measured from the centre of the ball to the water surface. An initial model is proposed, which ignores any resistive effects and the inertia of the water. Determine the prediction this initial model makes for the ratio h/d in terms of m, r and the density of water, ρ.

k) A sand timer is a sealed glass vessel with a narrow section acting as a constraint, so that sand can flflow through at a steady rate. A fififteen minute sand timer is shown in Figure 2 below. Unlike a liquid, the rate of flflow of sand grains through the constrained section is independent of the height of the sand above.
Thus the rate of flflow of sand through the time can be expressed as a product of powers of the remaining relevant variables: where k is a dimensionless constant, ρ is the density of the sand, A is the cross sectional area at the narrowest point, and g is the gravitational fifield strength, and α, β, γ are numbers.
(i) By considering the units of the variables on each side of the equation, fifind the values of α, β and γ.
(ii) On the Moon, the gravitational fifield strength is gM = 1.6 N kg−1 . How long would the sand timer last on the Moon if it runs for 15 minutes on Earth? l) An excited neon-20 isotope travels with a velocity of 3.0 × 10⁶ ms ^-1 into a detector and disintegrates into an alpha particle and oxygen-16. The event produces an additional 6.25 MeV of kinetic energy. The oxygen nucleus leaves the event at right angles to the path of the original neon nucleus.
Determine the velocity of the alpha particle. Relativistic effects may be neglected.
1 eV = 1.6 × 10^-19 J

m) An aeroplane flflies due East along the equator at a constant low altitude and constant speed relative to the ground. On the aeroplane, a one kilogram mass is suspended on a spring balance and records a weight W1. The aeroplane then flflies due West along the equator, at the same altitude and speed, and measures a balance reading of W2. If the speed of the plane relative to the ground is 250 ms ^-1 , calculate the difference in apparent weights

n) Two glass bulbs are connected by a thin tube. One glass bulb has a volume of 75 cm ³, the other 150 cm ³ , and gas can move freely between them. Initially the system contains nitrogen at −12 ◦C and 0.91 × 105 Pa. The smaller bulb is then warmed to 24 ◦C, whilst the larger bulb is maintained at −12 ◦C.
Calculate the new pressure in the system. Assume the thermal expansion of the bulbs and the volume of the connecting tube are negligible.

o) Determine the current in the 6.0 Ω resistor shown in the Fig 3. The cells have no internal resistance. 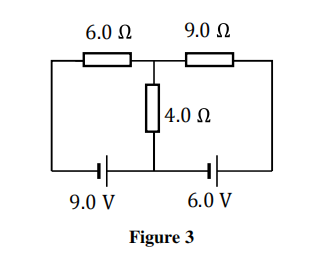p) An electrically isolated copper sphere of radius 2 mm is illuminated by light of wavelength 150 nm. Determine
(i) the maximum electric potential that the copper sphere can reach
(ii) the number of electrons lost reaching the maximum potential
(Work function of copper = 4.5 eV)

q) Three conducting spheres of radii R, R and R are mounted on insulating rods, and are well separated from each other. The R and R spheres are each charged to a potential V ,
whilst the R sphere is uncharged. Then a thin copper wire is used to brieflfly connect all three spheres. What fraction of the original charge on the two spheres is now on the R sphere?

r) The thermal power flflowing by conduction through a surface is proportional to the temperature difference across the surface, ∆θ, the area of the surface, A and inversely proportional to the thickness ∆x. The constant of proportionality is known as the thermal conductivity.
A 60 cm composite rod, of constant cross section, is made of 20 cm lengths of steel, copper and aluminium joined together. The rod is well insulated. The tip of the steel end of the rod is maintained at 100 ◦C and the tip of the aluminium end, at 0 ◦C. What are the temperatures at each of the two junctions of dissimilar metals?
Thermal conductivities are as follows: steel 60W m ^-1 K ^-1 ; copper 400Wm ^-1 K ^-1; aluminium 240W m ^-1 K ^-1.

s) A bicycle pump of cross-sectional area 4.0 cm2 has one end sawn off and a cork is fifitted into the end. The piston is pushed slowly inwards and the cork is fifired out with a popping sound which has a frequency of 512 Hz. The initial distance between the cork and the piston is 25 cm, with atmospheric pressure equal to 1.0 × 105 Pa and the speed of sound in air being 330 m s−1.
Calculate the force required to eject the cork.

t) A cup of tea cools from 30.2 ◦C to 29.7 ◦C in 1 minute, in an ambient temperature of 20.0 ◦C. Assuming the tea cools at a rate directly proportional to the temperature difference between the tea and the surroundings, calculate how long it will take for the tea to cool from 24.0 ◦C to 23.0 ◦C.