紫色彗星数学竞赛真题（2009年初中组）

PURPLE COMET MATH MEET April 2009
MIDDLE SCHOOL - PROBLEMS
©opyright Titu Andreescu and Jonathan Kane

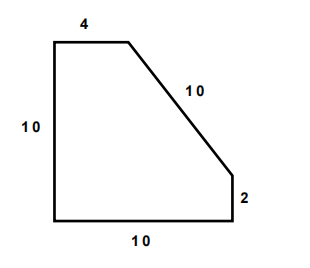
Problem 1
The pentagon below has three right angles. Find its area.

Problem 2
Let p₁ = 2, p₂ = 3, p₃ = 5, . . . be the sequence of prime numbers. Find the least positive even integer n so that p₁ + p₂ + p₃ + · · · + p_n is not prime.

Problem 3
The Purple Comet! Math Meet runs from April 27 through May 3, so the sum of the calendar dates for these seven days is 27 + 28 + 29 + 30 + 1 + 2 + 3 = 120. What is the largest sum of the calendar dates for seven consecutive Fridays occurring at any time in any year?

Problem 4
John, Paul, George, and Ringo baked a circular pie. Each cut a piece that was a sector of the circle. John took one-third of the whole pie. Paul took one-fourth of the whole pie. George took one-fifth of the whole pie. Ringo took one-sixth of the whole pie. At the end the pie had one sector remaining. Find the measure in degrees of the angle formed by this remaining sector.

Problem 5
A train car held 6000 pounds of mud which was 88 percent water. Then the train car sat in the sun, and some of the water evaporated so that now the mud is only 82 percent water. How many pounds does the mud weigh now?

 

【福利插播】

紫色彗星数学学术活动真题（2009年初中组）解析以及答案，最新年份真题，扫码免费领取：

Problem 6
Find n so that 20²⁰⁰⁹ = 10²⁰⁰⁰ · 40⁹ · 2ⁿ.

Problem 7
How many distinct four letter arrangements can be formed by rearranging the letters found in the word FLUFFY? For example, FLYF and ULFY are two possible arrangements.

Problem 8
Find the number of non-congruent scalene triangles whose sides all have integral length, and the longest side has length 11.

Problem 9
One plant is now 44 centimeters tall and will grow at a rate of 3 centimeters every 2 years. A second plant is now 80 centimeters tall and will grow at a rate of 5 centimeters every 6 years. In how many years will the plants be the same height?

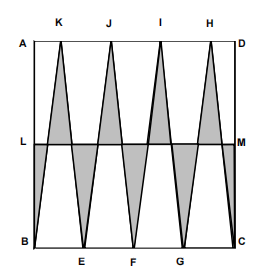
Problem 10
The diagram shows a 20 by 20 square ABCD. The points E, F, and G are equally spaced on side BC. The points H, I, J, and K on side DA are placed so that the triangles BKE, EJF, F IG, and GHC are isosceles. Points L and M are midpoints of the sides AB and CD, respectively. Find the total area of the shaded regions.

Problem 11
Aisha went shopping. At the first store she spent 40 percent of her money plus four dollars. At the second store she spent 50 percent of her remaining money plus 5 dollars. At the third store she spent 60 percent of her remaining money plus six dollars. When Aisha was done shopping at the three stores, she had two dollars left. How many dollars did she have with her when she started shopping?

Problem 12
In isosceles triangle ABC sides AB and BC have length 125 while side AC has length 150. Point D is the midpoint of side AC. E is on side BC so that BC and DE are perpendicular. Similarly, F is on side AB so that AB and DF are perpendicular. Find the area of triangle DEF.

Problem 13
How many subsets of the set {1, 2, 3, ..., 12} contain exactly one or two prime numbers.

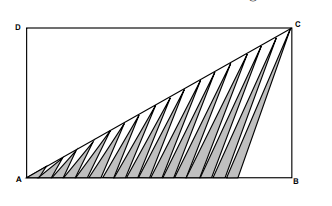
Problem 14
Rectangle ABCD measures 70 by 40. Eighteen points (including A and C) are marked on the diagonal AC dividing the diagonal into 17 congruent pieces. Twenty-two points (including A and B) are marked on the side AB dividing the side into 21 congruent pieces. Seventeen non-overlapping triangles are constructed as shown. Each triangle has two vertices that are two of these adjacent marked points on the side of the rectangle, and one vertex that is one of the marked points along the diagonal of the rectangle. Only the left 17 of the 21 congruent pieces along the side of the rectangle are used as bases of these triangles. Find the sum of the areas of these 17 triangles.

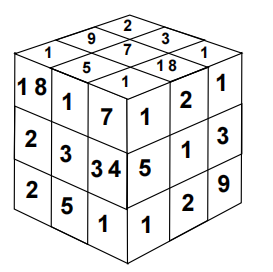
Problem 15
We have twenty-seven 1 by 1 cubes. Each face of every cube is marked with a natural number so that two opposite faces (top and bottom, front and back, left and right) are always marked with an even number and an odd number where the even number is twice that of the odd number. The twenty-seven cubes are put together to form one 3 by 3 cube as shown. When two cubes are placed face-to-face, adjoining faces are always marked with an odd number and an even number where the even number is one greater than the odd number. Find the sum of all of the numbers on all of the faces of all the 1 by 1 cubes.