- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2017-2018 BPhO英国物理奥赛第一轮第二部分真题及解析
British Physics Olympiad 2017-18
BPhO Round 1
Section 2
17th November 2017
This question paper must not be taken out of the exam room
Instructions
Time: 5 minutes reading time (NO writing) and 1 hour 20 minutes for writing on this section.
Questions: Only two questions out of the fifive questions in Section 2 should be attempted.
Each question contains independent parts so that later parts should be attempted even if earlier parts are incomplete.
Working: Working, calculations, explanations and diagrams, properly laid out, must be shown for full credit. The fifinal answer alone is not suffificient. Writing must be clear. If derivations are required, they must be mathematically supported, with any approximations stated and justifified.
Marks: Students are recommended to spend about 40 minutes on each question. The maximum mark for each question in Section 2 is 25, with a maximum of 50 marks from two questions only.
Instructions: You are allowed any standard exam board data/formula sheet.
Calculators: Any standard calculator may be used.
Solutions: Answers and calculations are to be written on loose paper or in examination booklets.
Graph paper and formula sheets should also be made available. Students should ensure that their name and their school are clearly written on each and every answer sheet.
Setting the paper: There are two options for sitting BPhO Round 1:
- Section 1 and Section 2 may be sat in one session of 2 hours 40 minutes plus 10 minutes reading time.
- Section 1 and Section 2 may be sat in two sessions on separate occasions, with 1 hour 20 minutes
plus 5 minutes reading time allocated for each section. If the paper is taken in two sessions on separate occasions, Section 1 must be collected in after the fifirst session and Section 2 handed out at the beginning of the second session.
Section 2
Question 2
a) A 50 Hz alternating current of 10 A (rms) passes along a copper wire whose diameter is 1.0 mm.
If copper contains 9.0 × 1022 free electrons per cm3 , estimate
(i) the maximum speed of the electrons, and
(ii) the maximum displacement of the electrons associated with the current.
b) A wire of length l and resistance R is extended by an amount ε such that ε l. If the volume of
the wire and its resistivity remain unchanged,
(i) Give an expression for the fractional change in R, i.e. ![]()
(ii) Calculate the new resistance of the wire if R = 100.0 Ω and ε/l = 0.001.
c) A non-linear electrical component is connected in a circuit in series with a supply of emf ε = 300 V and negligible internal resistance, and a resistor R of 4.0 kΩ. The relation between the current I through the non-linear component, and the potential difference across it, Vc, is given by I = AVc + BVc2 where A = 0.070 mA V−1, B = 0.0050 mA V−2.
(i) Obtain an algebraic expression for Vc.
(ii) Determine the current I through the non-linear component.
d) A metal hemisphere of radius 0.10 m is immersed near the centre of a large conducting tank containing a liquid of resistivity 60 Ω m. The plane surface of the hemisphere is level with the surface of the liquid.
(i) Find an expression for the resistance between two hemispherical shells within the liquid, concentric with the centre of the metal hemisphere, having radii r and (r + δr) respectively.
(ii) Calculate the resistance between the hemisphere and the tank.
Question 3
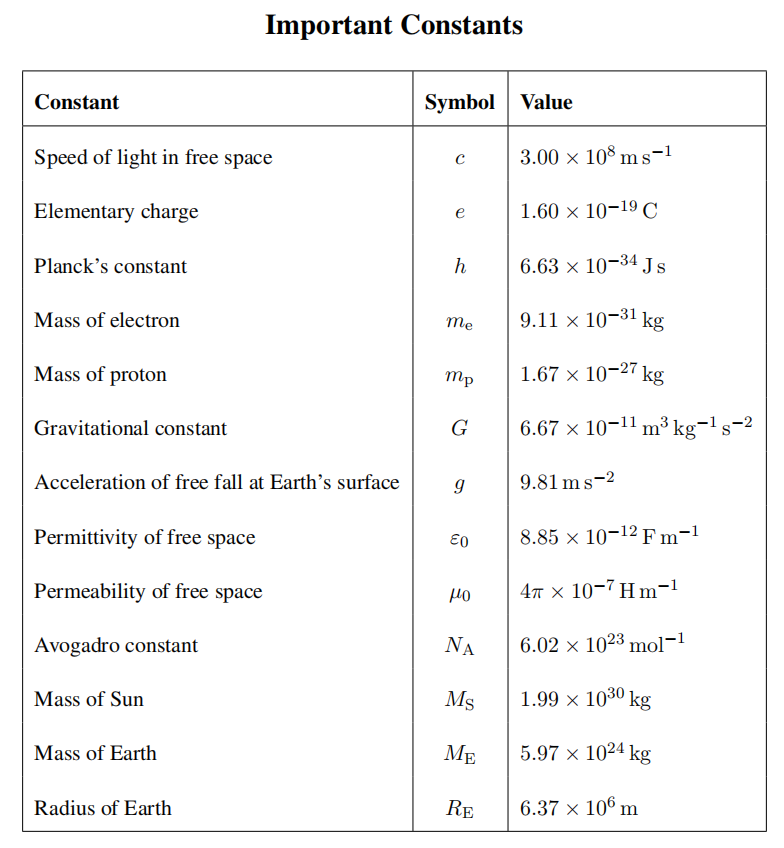
A tug boat winch is fifitted with friction brakes that slip when the tension in the winch cable reaches 50 kN. The winch is mounted on a 450 tonne tug which is to tow a flfloating barge of mass 6300 tonne. The barge is initially at rest while the tug moves away from it at. The speed of the tug at the moment that the cable becomes taut is 2.5 m s−1 . At that moment the winch friction brakes start slipping in order to prevent the cable from breaking. The thrust exerted on the tug by its propeller is 35 kN. The winch and arrangement might look something like Figure 1a and Figure 1b:
a) Calculate
(i) The time during which the brakes are slipping,
(ii) The common velocity of the tug and the barge when the brakes stop slipping.
(iii) What length of cable runs out of the drum of the winch during the time the brakes are slipping?
- b) In a different geometry the winch is used to
haul sand up from the bottom of a dry dock using a crane constructed from a very light framework of girders. The crane geometry can be seen in the diagram of Figure 2. The crane is fifixed to the horizontal dock side at points A and B. The dimensions of the sides CB, CD and BD are as shown, the girder CB is vertical, and the winch is hauling a load of weight 15W.
(i) Find the magnitude of the force exerted on D by the member BD,
(ii) The tension in the member CD.
(iii) If the force on the crane at A by the ground acts vertically downwards and has a magnitude 31W, fifind the distance AB in terms of L.

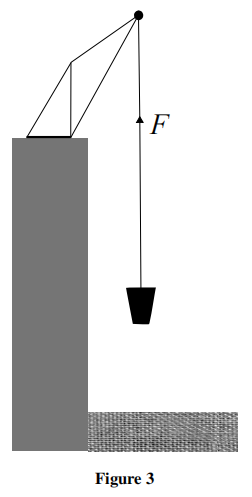
c) The bucket of mass m is drawn up by the winch cable which exerts a steady force F upwards, shown in Figure 3. The bucket starts from rest and initially contains a mass m0 of sand. The sand leaks out at a constant rate so that the bucket is empty after time t, which occurs before it reaches the top of the dry dock wall.
In terms of F, m0, m, t and g (the gravitational fifield strength), what is the velocity v of the bucket when it is just empty? The friction brakes do not slip.
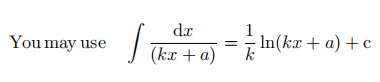
Question 4
a) Calculate the smallest angle of incidence for light incident on the face of a 60◦ prism of refractive index 1.5, such that all of the light on the second face is totally reflflected. Draw a large diagram to show the path of the light and the angles.
b) Consider the step index optical fifibre shown in Figure 4
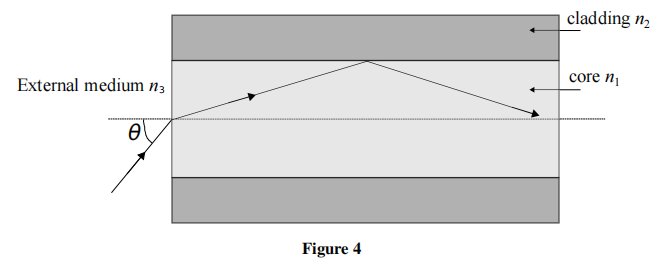
The core, cladding and external medium have refractive indices n1, n2, and n3, respectively.The acceptance angle θ for light entering the core of the fifibre will allow transmission without loss providing the angle θ between the incident ray and the axis is smaller than the maximum acceptance angle θm.
(i) Obtain an expression for sin θm in terms of n1, n2, and n3.
Hint: cos2θ = 1 − sin2θ
(ii) Light enters the fifibre optic at angles between θ = 0◦ and θm. Given a step index fifibre with a core refractive index of 1.48585, and a cladding refractive index of 1.45641, determine the time broadening of the leading edge of a square pulse over a distance of 100 km.
(iii) If multiple, very brief, square pulses of light are sent down the cable at frequency fp, calculate the maximum possible pulse frequency over this 100 km distance, such that the pulses do not overlap.
(iv) Show that in general the time spread of a pulse ∆t, in a fifibre of length L, is given by
∆t =![]() ∆n, with ∆n the difference in refractive indices between core and cladding, and c, the speed of light in the optical fifibre.
∆n, with ∆n the difference in refractive indices between core and cladding, and c, the speed of light in the optical fifibre.
c) A ray of light from a point source O on the principal axis of a thin converging lens, passing through the lens, is brought to a focus at the image point P also on the principal axis, and shown in Figure 5.
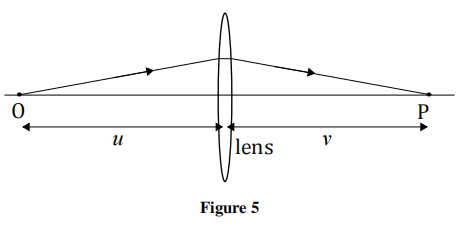
One form of an equation for a thin lens, relating object and image distances, u, v to the focal length f is
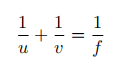
By taking the limit u → ∞, explain what the length f represents for a lens.
d) Rays of light from a point source on the principal axis, passing through a converging lens by different paths and reaching a focus point on the principal axis, can be considered to do so by following paths which all have an equal time of travel. (This is a simplifified form of a more general principle — Fermat’s Principle of Least Time).
A flflat, thin, circular disc of transparent material is made so that its refractive index n varies with the distance r from the principal axis normal to the centre of the disc, according to the equation n = no(1 − kr2), where no and k are constant.
(i) By considering the times taken by light travelling by different paths (take a path not on the principal axis), show for rays travelling very close to the principal axis that the thin disc can behave as a lens. i.e. obtain an expression for ![]() , if the thickness of the disc is d, with d 《u, v.
, if the thickness of the disc is d, with d 《u, v.
(ii) Derive an expression for its focal length in terms of d, k and no.
Question 5
a) A simple pendulum of string length l, with a bob of mass m, containing charge Q, is in a horizontal electric fifield of magnitude E.
(i) Determine the angle of the string with respect to the vertical when the bob is in equilibrium.
(ii) If the electric fifield now points vertically downwards and there is a small negative charge on the bob, −Q, such that the string remains taut, what would be the period of oscillation of the bob once perturbed?
(iii) Give the condition relating Q, E, m and g, such that oscillations will occur when the bob is perturbed.
b) Equal and opposite charges +Q and −Q are a distance of 2a Taking the midpoint between them as the origin O, fifind the electric potential and the magnitude of the fifield strength, at a point P which is distance r(r 》a) from O, when
(i) P is on the line passing through the charges;
(ii) When P is on a perpendicular bisector of the line joining the charges.
c) Equal and opposite charges separated by a small distance constitute a dipole. A hydrogen chloride molecule may be treated as a dipole in which an electron is separated from a positive charge of equal magnitude by a distance of 2 × 10−11 m. Calculate the work done needed to turn the molecule, which is lying parallel to a fifield of 3 × 105 V m−1 , through an angle of 180◦.
d) In a simple model of a thundercloud, an upper cylindrical shaped region (axis vertical) contains a net positve charge and the lower cylindrical shaped region of the cloud a net negative charge, as shown in Figure 6. The upper region, from 9 km to 12 km height, with a radius of 5 km has a charge density of 0.21 nC m-3 , whilst the lower region from 2 km to 9 km high, also with a radius of 5 km, has a charge density of −0.18 nC m-3.

(i) Calculate the magnitudes of the positive and negative charges in each region.
In order to determine the fifield strength at the ground due to these charges, we can aproximate these two volumes of charge as two point charges at the centres of each of the two regions (at heights 10.5 km and 5.5 km respectively). The ground is a good conducting plane surface and so charges will be induced in the surface. The effect of this induced charge can be simulated by considering a charge of equal magnitude but opposite sign at the same distance h below the surface as the real charge at height h above the surface. The fifield at the surface is then calculated from the fifield of the real charge at the surface added to the fifield due to the image charge at the surface.
(ii) For the two charges calculated, with their two image charges of opposite signs, calculate the strength of the electric fifield at the surface of the Earth directly below the thundercloud.
(iii) If a two metre tall person stands with his feet on the ground in this region, what is the magnitude and polarity of the potential at his head? Take the potential of the ground to be
Question 6
a) Sea waves of frequency f are moving North with velocity c. A small boat moves South with a velocity u, both velocities being measured with respect to the land. By counting the number of waves moving past the boat in a time ∆t or otherwise, show that the boat will be moving up and down with a frequency f0 given by
 b)(i) A source of sound, emitting a single note of frequency f is moving towards a stationary observer with speed vs. Show that if the air is stationary, the frequency f0 detected by the observer is given by
b)(i) A source of sound, emitting a single note of frequency f is moving towards a stationary observer with speed vs. Show that if the air is stationary, the frequency f0 detected by the observer is given by
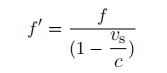
where c is the speed of sound in air. You may wish to consider a time ∆t, and how many waves are emitted by the source, how far the waves and the source each move in this time, the wavelength the observer then detects, or any other approach.
(ii) What would be the value of ∆f = f, − f if the source is moving away from the observer at a speed vs = c/2 ?

c) The above formula can be applied to electromagnetic waves.
(i) Show that the observed frequency of an absorption line of emitted frequency f in the spectrum of the Sun should vary between f + δf and f − δf where
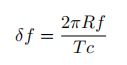
in which R is the radius of the Sun, and T the period of rotation.
(ii) Given that the density of the Sun is 1.4 × 103 kg m−3 , the mass is 2.0 × 1030 kg and the equatorial rotation period is 24.5 days, estimate the fractional frequency shift,![]() , for the peak in the visible spectrum at 550 nm.
, for the peak in the visible spectrum at 550 nm.
d) Two stars labelled A and B separated by a distance a = 19.8 AU form a binary pair, gravitationally bound, orbiting a common centre of mass with a period T = 50.1 y. Star A, with mass mA is at radius RA from the centre of mass, and star B, a very faint white dwarf, of mass mB orbits at radius RB. The stars have circular orbits with the plane of the orbit lying along the line of sight from the Earth. Only the brightest of the two stars can be observed through a telescope, and it is found that a spectral line of 656.3 nm in the lab varies by ±0.0235 nm when observed in the bright star.

END OF SECTION 2
扫描下方二维码获取参考答案及详解:

翰林物理学术活动课程体系流程图
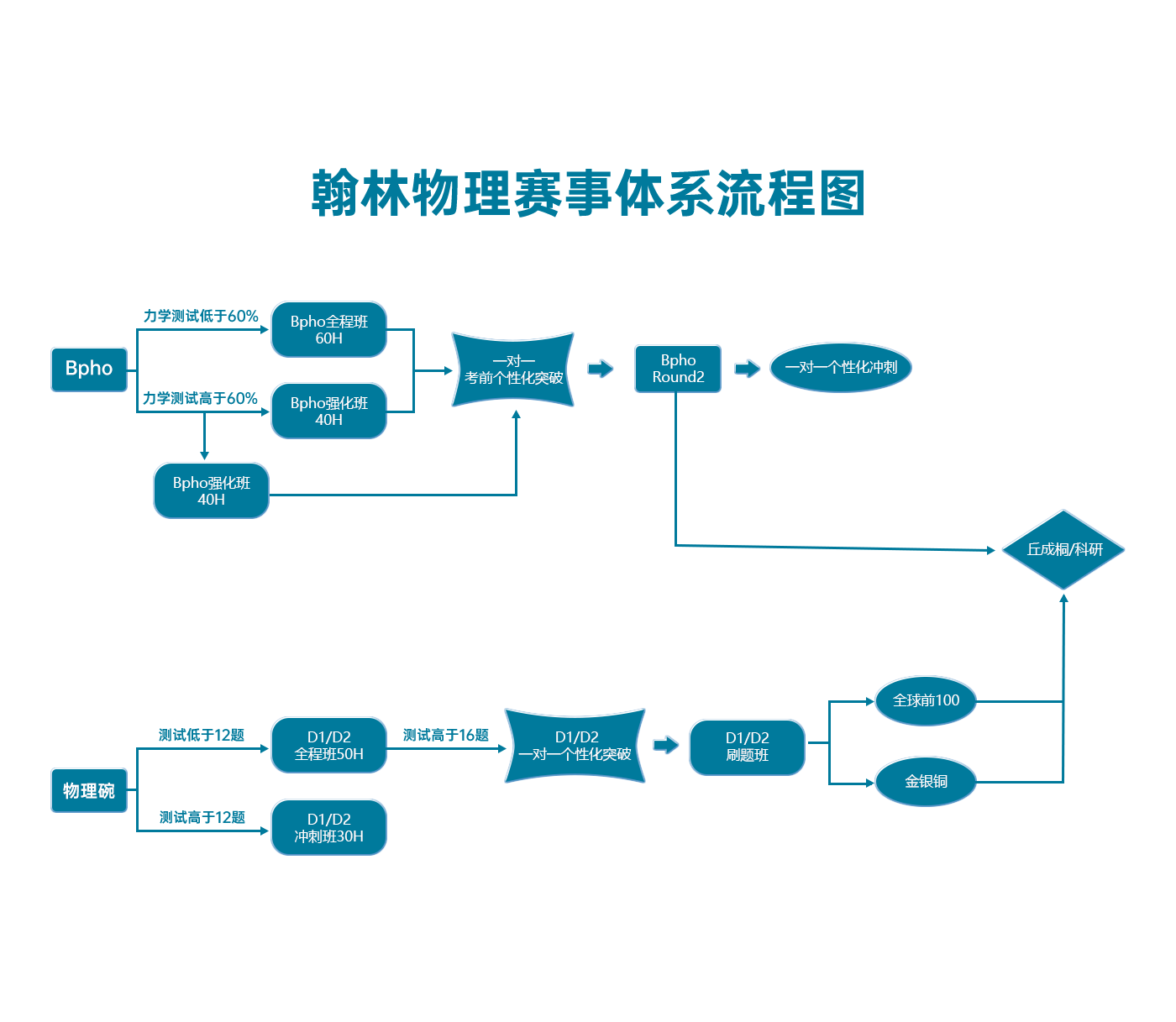

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









