- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2017-2018 BPhO英国物理奥赛第一轮第一部分真题及解析
British Physics Olympiad 2017-18
BPhO Round 1
Section 1
17th November 2017
This question paper must not be taken out of the exam room
Instructions
Time: 5 minutes reading time (NO writing) and 1 hour 20 minutes for writing on this section.
Questions: Students may attempt any parts of Section 1, but are not expected to complete all parts.
Working: Working, calculations, explanations and diagrams, properly laid out, must be shown for full credit. The fifinal answer alone is not suffificient. Writing must be clear.
Marks: A maximum of 50 marks can be awarded for Section 1. There is a total of 94 marks allocated to the problems of Question 1 which makes up the whole of Section 1.
Instructions: You are allowed any standard exam board data/formula sheet.
Calculators: Any standard calculator may be used.
Solutions: Answers and calculations are to be written on loose paper or in examination booklets.Graph paper and formula sheets should also be made available. Students should ensure that their name and their school are clearly written on each and every answer sheet. Number each question clearly.
Setting the paper: There are two options for sitting BPhO Round 1:
a.Section 1 and Section 2 may be sat in one session of 2 hours 40 minutes plus 10 minutes reading time.
b.Section 1 and Section 2 may be sat in two sessions on separate occasions, with 1 hour 20 minutes plus 5 minutes reading time allocated for each section. If the paper is taken in two sessions on separate occasions, Section 1 must be collected in after the fifirst session and Section 2 handed out at the beginning of the second session.

Question 1
a) Physicists sometimes use the approximation that light travels in a vacuum at a speed of 1 foot in 1 ns. What is the percentage error in using this value?
(1.000 m = 1.094 yards and 1.000 yard = 3.000 feet)
b) A window cleaner’s ladder shown in Figure 1 is narrower at the top than the bottom. It has a weight of 350 N and a length of 5.0 m. When it lies flflat on the ground, a force of 80 N is needed to lift the narrow end off the ground.
(i) How far is the centre of mass from the narrow end?
(ii) What force is required to lift the wide end of the ladder off the ground?
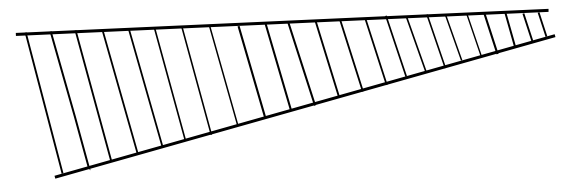
Figure 1
- c) A particle moves in a straight line with an intial acceleration of 10ms-2 . The acceleration decreases uniformly with time until, after ten seconds, the acceleration is 5ms-2 , and from then on the acceleration remains constant. If the intial velocity is 100ms-1,
(i) fifind when the velocity has doubled;
(ii) sketch a graph of the velocity against time.
- d) A student standing at a distance a from a vertical wall kicks a ball from ground level with velocity V at an angle α to the horizontal in a plane perpendicular to that of the wall. The ball strikes the wall and rebounds. The coeffificient of restitution for the collision is e = 2/3. The ball fifirst strikes the ground at a distance 2a from the wall. e is the ratio of the components of velocity at normal incidence to the wall, before and after collision;

Find a in terms of V, α and g, the gravitational fifield strength.
e) A helicopter of total mass 1000 kg is able to remain in a stationary position by imparting a uniform downward velocity to a cylinder of air below it of effective diameter 6 m. Assuming the density of air to be 1.2 kg m−3 , calculate the downward velocity of the air.

(i) the position vector of the ship at 2 p.m.,
(ii) the velocity vector of the motor boat,
(iii) the time of interception.
g) In a factory heating system, water enters the radiators at 60 ◦C and leaves at 38 ◦C. The system is replaced by one in which steam at 100 ◦C is condensed in the radiators, the condensed steam leaving at 82 ◦C. What mass of steam will supply the same heat energy as 1.00 kg of hot water described in the fifirst instance? (The latent heat of vaporisation of water is 2.260 × 106 J kg−1 at 100 ◦C. The specifific heat capacity of water is 4200 J kg−1 ◦C−1 .)
h) A cell, a resistor and an ammeter of negligible resistance are connected in series and a current of 0.80 A is observed to flflow when the resistor has a value of 2.00 Ω. When a resistor of 5.00 Ω is connected in parallel with the 2.00 Ω resistor, the ammeter reading is 1.00 A.
Calculate the emf and the internal resistance of the cell.
i) A battery with an emf of 6 V can produce a maximum current of 3 A. A resistor is connected to the terminals whose value is such that the power dissipated in it is a maximum. Calculate the maximum energy which can be dissipated in the external resistor in one minute.
j) Calculate the number of photons emitted in a one nanosecond (10−9 s) pulse of light from a 0.5 mW laser of wavelength 639 nm.
k) A lead ball is attached to the end of a light metal rod of length l, the other end being attached to a horizontal axle of negligble friction. The rod is given an intial impulse and swings round in a vertical circle. When it is at the top of the circle, the tension in the rod is zero. What is the tension in the rod at the lowest point of its swing?
l) Some sand is sprinkled onto a loudspeaker cone which is pointing vertically upwards. The louspeaker is driven in simple harmonic motion when attached to a signal generator and the frequency is gradually raised. At a particular frequency, when the amplitiude of oscillation is 0.20 mm, the sand begins to lose contact with the cone. At what frequency does this occur?
m) Two radio stations on the equator, diametrically opposite each other, communicate by sending and
receiving radio signals that are tangential to the Earth’s surface via two geostationary satellites
in circular orbits at 3.59 × 104 km above the Earth’s surface. Calculate the time delay between
sending and receiving a signal.
n) A thin fifilm of transparent material of refractive index 1.52 and thickness 0.42 µm forms a thin
coating on glass of refractive index 1.60. It is viewed by reflflection with white light at normal
incidence. What visible wavelength in vacuo is most strongly reflflected?
o) Monochromatic light of wavelength 600 nm is incident on two vertical slits hence producing two coherent sources. Before the light leaving these slits overlaps and interferes, each beam passes through a tube 5.0 cm long. One of the tubes is now gradually evacuated and it is noted that the fringe pattern shifts 25 fringes. Calculate the refractive index of air.
p) A submerged wreck is lifted from a dock basin by means of a crane to which is attached a steel cable 10 m long of cross-sectional area 5.0 cm2 and Young modulus 5.0 × 1010 Pa. The material being lifted has a mass of 1.0 × 104 kg and mean density 8000 kg m−3 . Find the change in extension of the cable as the load is lifted clear of the water. Assume that at all times the tension in the cable is the same throughout its length. (Density of water is 1000 kg m−3 .)
q) A uniform beam AOB, O being the midpoint of AB, mass M, rests on three vertical springs with
stiffness constants k1, k2, k3 at A, O and B respectively. The bases of the springs are fifixed to a
horizontal platform. Determine the compression of the springs and their compressional forces in
the following two instances:
(i) k1 = k3 = k and k2 = 2k
(ii) k1 = k, k2 = 2k and k3 = 3k
r) A pond is covered by a layer of ice 5 cm How long will it be before the ice is 10 cm thick
if the air temperature stays constant at −10 ◦C?
Assume the density of ice = 900 kgm-3 ; the latent heat of fusion of ice = 330 kJ kg-1 ; the thermal conductivity of ice = 2.1W m-1 K-1.
The power flflowing perpendicular to the faces through a uniform material is given by power flflow ![]() , in which λ is the thermal conductivity of the material, TH is the hotter temperature at one face of the material, TC is the colder temperature on the other face, A is the area of a face, and x is the thickness of the material.
, in which λ is the thermal conductivity of the material, TH is the hotter temperature at one face of the material, TC is the colder temperature on the other face, A is the area of a face, and x is the thickness of the material.
END OF SECTION 1
扫描下方二维码获取参考答案及详解:

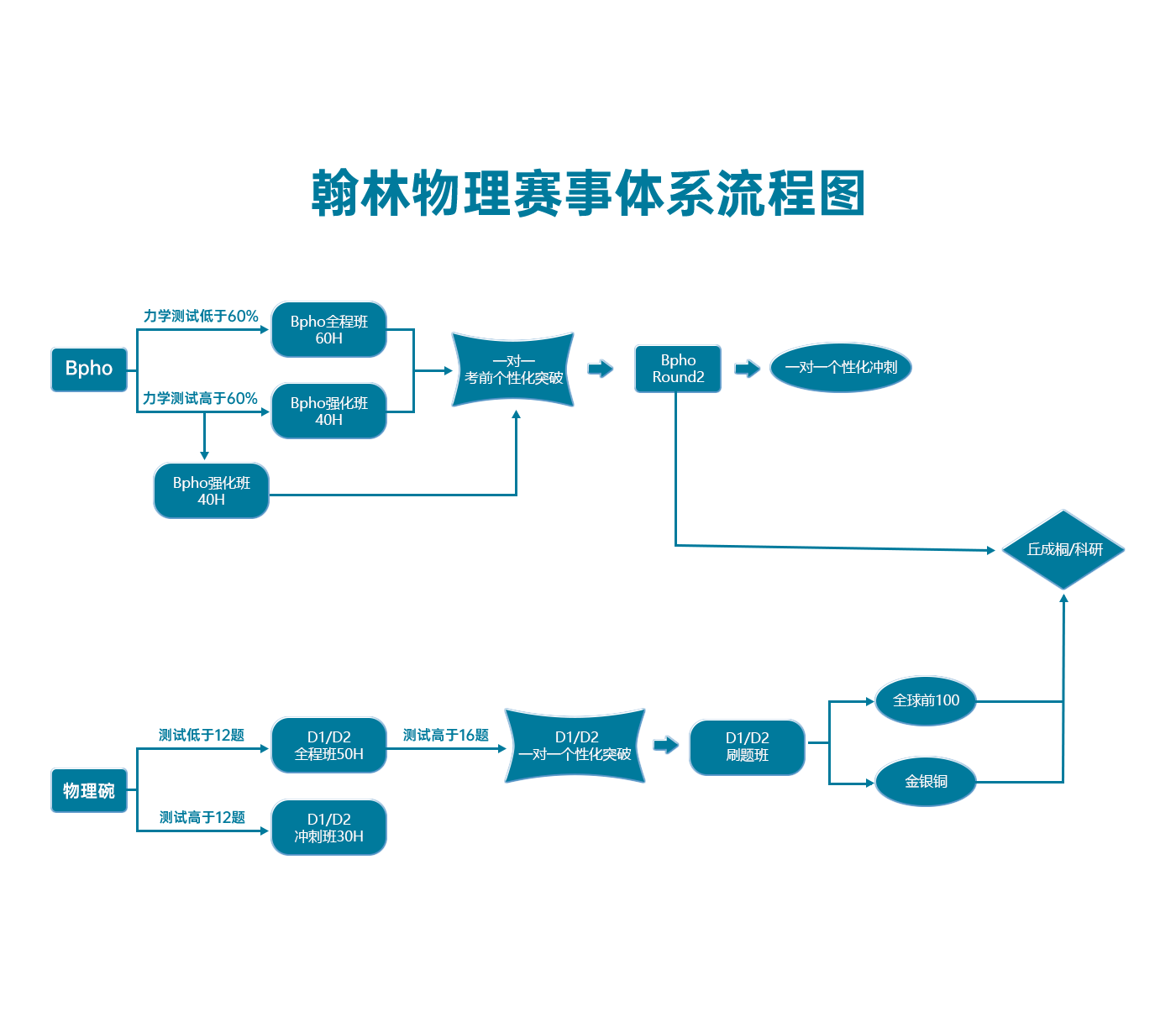
翰林物理学术活动课程体系流程图


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








