- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2020AMC8 真题及答案
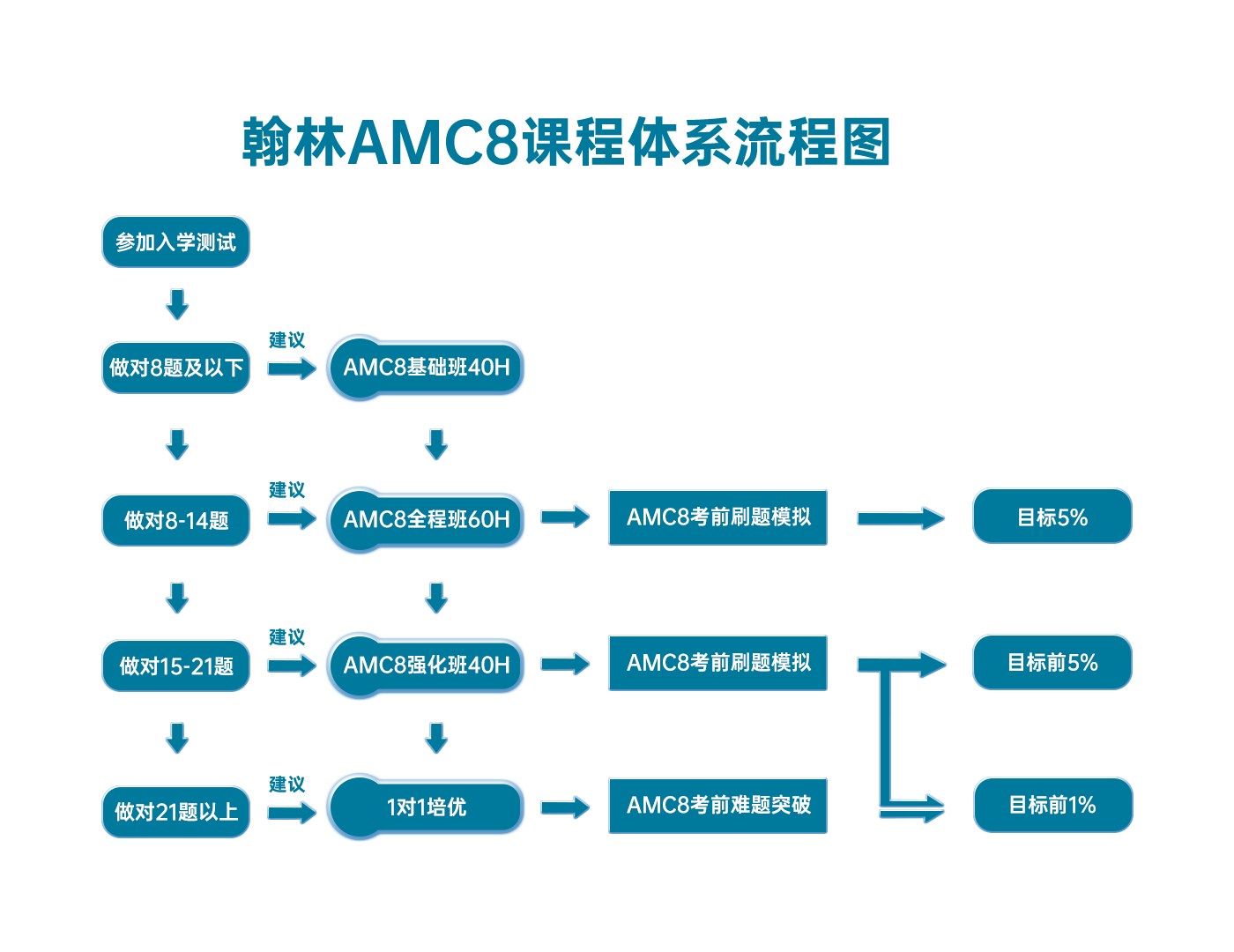
翰林AMC8课程体系流程图
Problem 1
Luka is making lemonade to sell at a school fundraiser. His recipe requires times as much water as sugar and twice as much sugar as lemon juice. He uses cups of lemon juice. How many cups of water does he need?
(A)6 (B)8 (C)12 (D)18 (E)24
Problem 2
Four friends do yardwork for their neighbors over the weekend, earning $15,$20,$25 and$40, respectively. They decide to split their earnings equally among themselves. In total how much will the friend who earned $40 give to the others?
(A)$5 (B)$10 (C)$15 (D)$20 (E)$25
Problem 3
Carrie has a rectangular garden that measures feet by feet. She plants the entire garden with strawberry plants. Carrie is able to plant strawberry plants per square foot, and she harvests an average of strawberries per plant. How many strawberries can she expect to harvest?
(A)560 (B)960 (C)1120 (D)1920 (E)3840
Problem 4
Three hexagons of increasing size are shown below. Suppose the dot pattern continues so that each successive hexagon contains one more band of dots. How many dots are in the next hexagon?
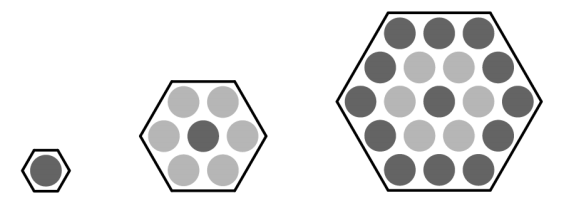
(A)35 (B)37 (C)39 (D)43 (E)49
Problem 5
Three fourths of a pitcher is fifilled with pineapple juice. The pitcher is emptied by pouring an equal amount of juice into each of 5 cups. What percent of the total capacity of the pitcher did each cup receive?
(A)5 (B)10 (C)15 (D)20 (E)25
Problem 6
Aaron, Darren, Karen, Maren, and Sharon rode on a small train that has fifive cars that seat one person each. Maren sat in the last car. Aaron sat directly behind Sharon. Darren sat in one of the cars in front of Aaron. At least one person sat between Karen and Darren. Who sat in the middle car?
(A)Aaron (B)Darren (C)Karen (D) Maren (E)Sharon
Problem 7
How many integers between 2020 and 2400 have four distinct digits arranged in increasing order? (For example,2347 is one
integer.)
(A)9 (B)10 (C)15 (D)21 (E)28
Problem 8
Ricardo has 2020 coins, some of which are pennies ( -cent coins) and the rest of which are nickels ( -cent coins). He has at least one penny and at least one nickel. What is the difference in cents between the greatest possible and least possible amounts of money that Ricardo can have?
(A)8062 (B)8068 (C)8072 (D)8076 (E)8082
Problem 9
Akash's birthday cake is in the form of a 4X4X4 inch cube. The cake has icing on the top and the four side faces, and no icing on the bottom. Suppose the cake is cut into 64 smaller cubes, each measuring X1X1X inch, as shown below. How many small pieces will have icing on exactly two sides?
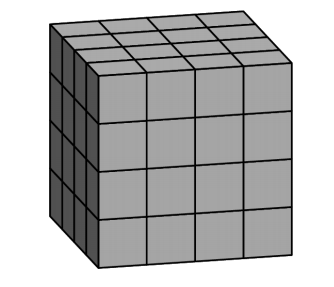
(A)12 (B)16 (C)18 (D)20 (E)24
Problem 10
Zara has a collection of marbles: an Aggie, a Bumblebee, a Steelie, and a Tiger. She wants to display them in a row on a shelf, but does not want to put the Steelie and the Tiger next to one another. In how many ways can she do this?
(A)6 (B)8 (C)12 (D)18 (E)24
Problem 11
After school, Maya and Naomi headed to the beach, miles away. Maya decided to bike while Naomi took a bus. The graph below shows their journeys, indicating the time and distance traveled. What was the difference, in miles per hour, between Naomi's and Maya's average speeds?
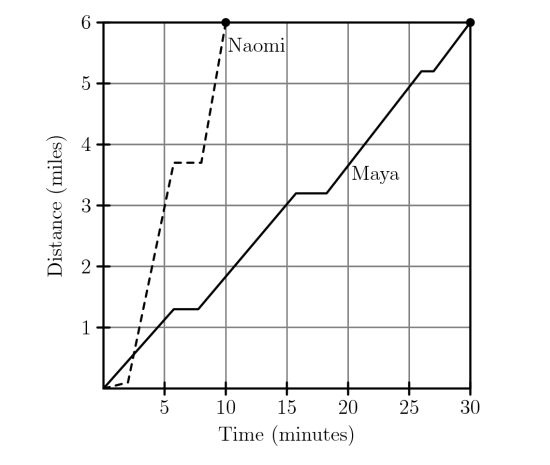
(A)6 (B)12 (C)18 (D)20 (E)24
Problem 12
For a positive integer n, the factorial notation n! represents the product of the integers from n to 1. (For example,6!=6·5·4·3·2·1) What value of N satisfifies the following equation?
5!·9!=12·N!
(A)10 (B)11 (C)12 (D)13 (E)14
Problem 13
Jamal has a drawer containing 6 green socks,18purple socks, and 12 orange socks. After adding more purple socks, Jamal noticed that there is now a 60% chance that a sock randomly selected from the drawer is purple. How many purple socks did Jamal add?
(A)6 (B)9 (C)12 (D)18 (E)24
Problem 14
There are 20 cities in the County of Newton. Their populations are shown in the bar chart below. The average population of all the cities is indicated by the horizontal dashed line. Which of the following is closest to the total population of all 20 cities?
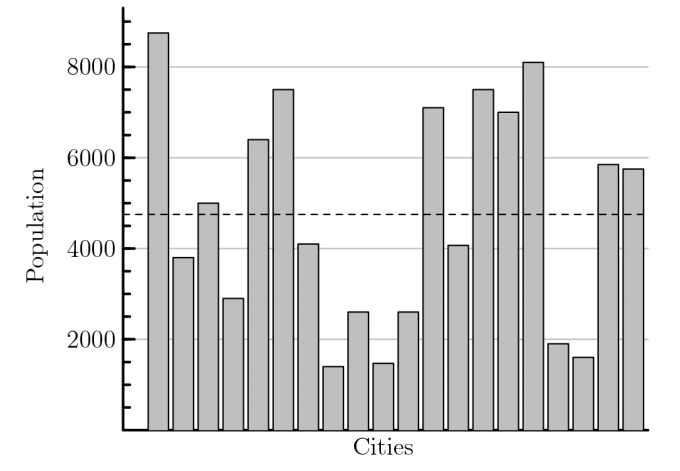
(A)65,000 (B)75,000 (C)85,000 (D)85,000 (E)105,000
Problem 15
Suppose 15% of equals 20% of y.What percentage of x is y?
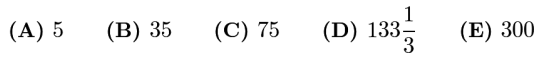
Problem 16
Each of the points A,B,C,D,E,and in the fifigure below represents a different digit from1 to 6.Each of the fifive lines shown passes through some of these points. The digits along each line are added to produce fifive sums, one for each line. The total of the fifive sums is 47.What is the digit represented by B?
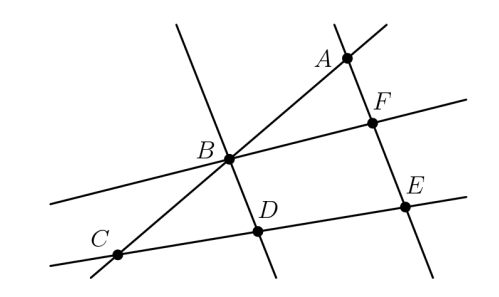
(A)1 (B)2 (C)3 (D)4 (E)5
Problem 17
How many factors of 2020 have more than 3 factors? (As an example,12 has 6 factors, namely 1,2,3,4,5,6, and 12)
(A)6 (B)7 (C)8 (D)9 (E)10
Problem 18
Rectangle ABCD is inscribed in a semicircle with diameter ![]() as shown in the fifigure. Let DA=16,and let FD=AE=9.What is the area of abcd?
as shown in the fifigure. Let DA=16,and let FD=AE=9.What is the area of abcd?
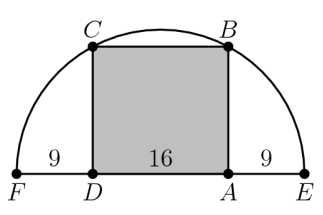
(A)240 (B)248 (C)256 (D)264 (E)272
Problem 19
A number is called flflippy if its digits alternate between two distinct digits. For example, 2020 and 37373 are flflippy, but 3883 and 123123 are not. How many fifive-digit flflippy numbers are divisible by 15?
(A)3 (B)4 (C)5 (D)6 (E)8
Problem 20
A scientist walking through a forest recorded as integers the heights of trees standing in a row. She observed that each tree was either twice as tall or half as tall as the one to its right. Unfortunately some of her data was lost when rain fell on her notebook. Her notes are shown below, with blanks indicating the missing numbers. Based on her observations, the scientist was able to reconstruct the lost data. What was the average height of the trees, in meters?

(A)22.2 (B)24.2 (C)33.2 (D)35.2 (E)37.2
Problem 21
A game board consists of 64 squares that alternate in color between black and white. The fifigure below shows square P in the bottom row and square Q in the top row. A marker is placed at P.A step consists of moving the marker onto one of the adjoining white squares in the row above. How many 7-step paths are there from P to Q?(The fifigure shows a sample path.)

(A)28 (B)30 (C)32 (D)33 (E)35
Problem 22
When a positive integer N is fed into a machine, the output is a number calculated according to the rule shown below.
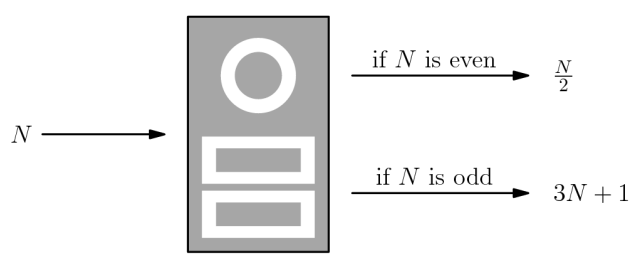
For example, starting with an input of N=7,the machine will output3·7+1=22.Then if the output is repeatedly
inserted into the machine fifive more times, the fifinal output is 26.
7→22→11→34→17→52→26
When the same 6-step process is applied to a different starting value of N,the fifinal output is 1.What is the sum of all such
integers N?
N→____→____→____→____→____→1
(A)73 (B)74 (C)75 (D)82 (E)83
Problem 23
Five different awards are to be given to three students. Each student will receive at least one award. In how many different ways can the awards be distributed?
(A)120 (B)150 (C)180 (D)210 (E)240
Problem 24
A large square region is paved with n2 gray square tiles, each measuring inches on a side. A border d inches wide surrounds each tile. The fifigure below shows the case for n=3. When n=24, the 576 gray tiles cover 64% of the area of the large square region. What is the ratio ![]() for this larger value of n?
for this larger value of n?

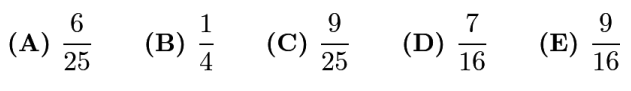
Problem 25

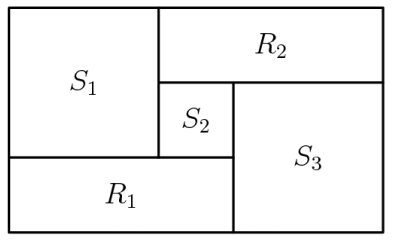
(A)651 (B)655 (C)656 (D)662 (E)666


早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








