AMC在知识点的储备上其实并没有超过初高中生的能力范围,所有的AMC考题无论是简单题还是难题、超难题可以说100%都可以使用同学们现有的知识去解决。
想要在AMC考试中异军突起,拿到AIME的入场券无非在于下面两项比较重要的能力:
1.掌握更多的数学知识
比如calculus,比如matrix,比如complex plane。往往一道比较“难度”的题目,其实只是某种高阶知识的基础性题目; 一道很难用叠加概率算出的题目,calculus的定积分思想简直就像“一键解题”。
2.改变以往的数学思维模式
提高解决问题的技巧。
大部分同学可能并没有时间去学习calculus,linear algebra,complex plane等等稍微偏离高中基本数学基础的知识,那么这个时候我们在做AMC题目的时候一定要有一个这样的一种认知:“数学学术活动只要解决问题即可,不需要得到类似于1+1=2的定解”,怎样快速并相对准确得到我们想要的答案将是AMC备考大家要掌握的核心技能。
这里我们给大家举个例子让同学们感受一下,其实一道毫无头绪的“难题”我们也是可以利用初高中知识飞速畅快解题的:

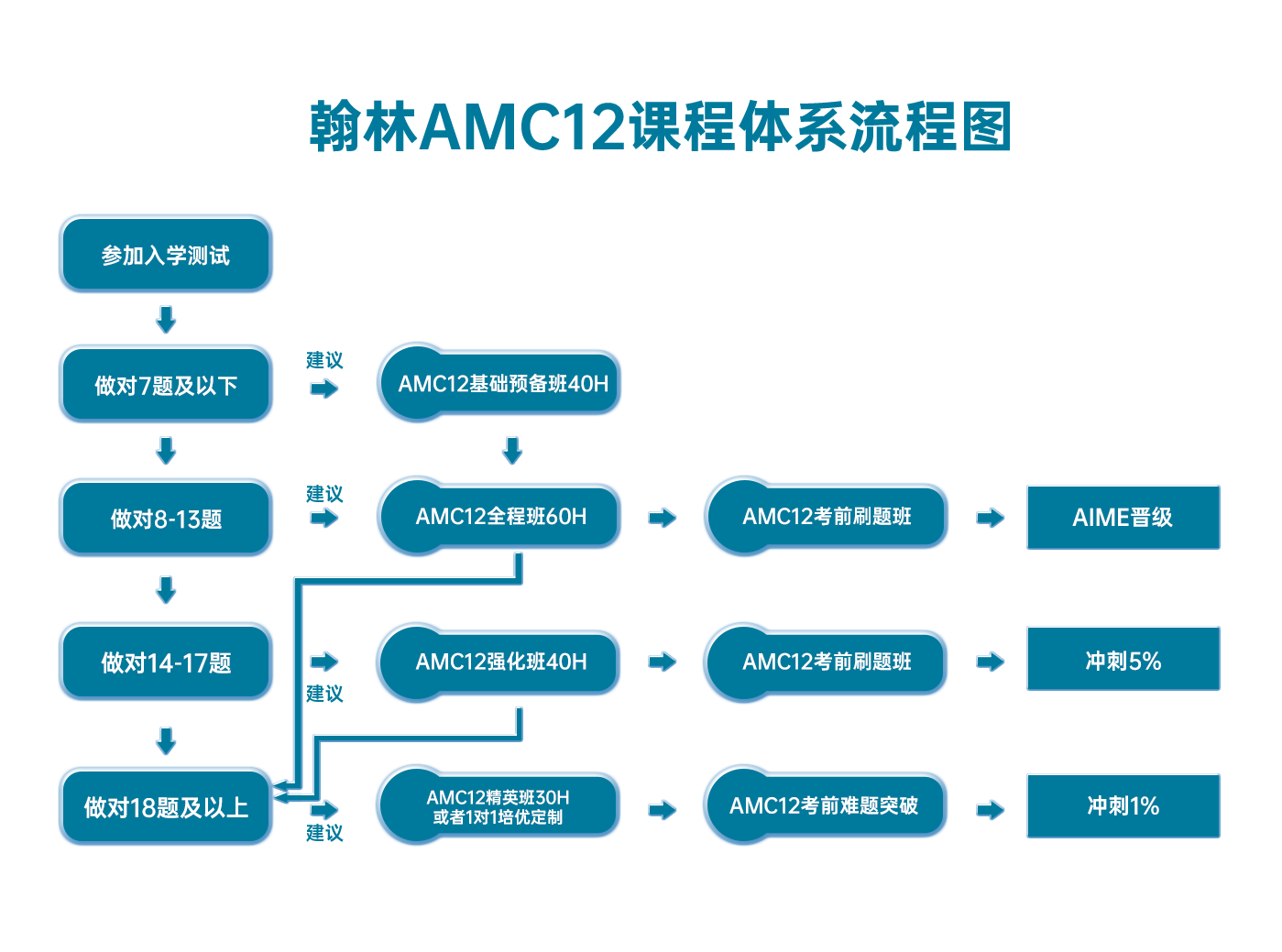
我们看下这道2017年A卷的第15题,需要我们确定多个三角函数叠加在一起的函数的第一个positive root,“普通”同学可能直接懵逼,“大佬”同学们心里想的是这个:
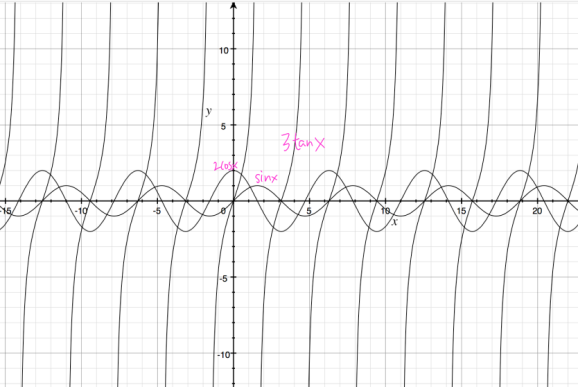
在尝试了半天构建三者在叠加在一起的函数寻找零点后宣告放弃。更有“奇葩”同学宣称一定要找到这个zero point的exact value,做了如下尝试:
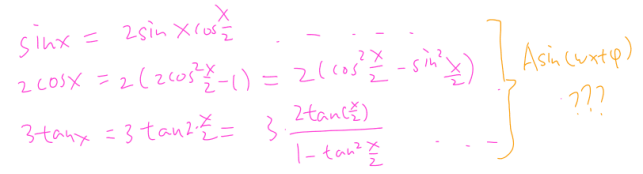
然后就没有然后了。
其实无论是哪种同学的第一反应我们都能够理解,往往在寻找零点的时候,大家已经习惯了用计算器去寻找,或者把它化成我们熟悉的函数再去用公式求解。但其实这道题大家只要拥有对sinx、cosx、tanx角度转动的基本了解以及按照“零点左右发生正负改变”的思路去想就能够秒出答案:
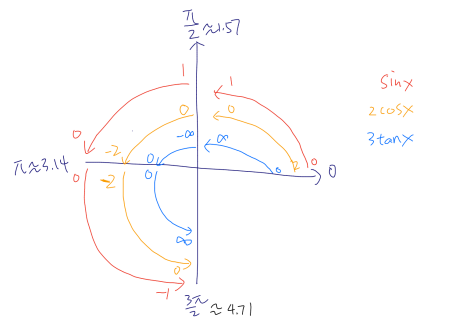
我们可以看到其实大家要做的只有两件事:
确定这三个函数在第一、二、三qudrant的函数值变化情况,可以看出在first quadrant三者叠加always positive,在second quadrant三者叠加alway negative,在third quadrant三者的叠加出现了“正负交替”,from -2 to positive infinity.
因此第一个zero point 一定出现在third quadrant,但是因为third quadrant的radians是从3.14到4.71,我们无法用该信息排除其中任一选项,那么下面我们可以选取一个相对熟悉的角比如(5pi/ 4)来做下区分:
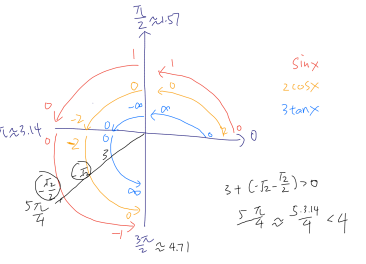
这里我们可以看出在(5pi/4)处,三个函数的叠加值是大于0的也就是说在这个角度之前就发生了正负的交替,并且(5pi/4)是小于4的,那么我们就完全确定了在3到4之间发生了正负交替,那么第一个zero point一定是在[3,4]这个区间之内的,选D选项。
通过这道题,大家也可以发现,如果我们找对了“路子”,两分钟之内我们就可以完成对这道题从切入到解决的所有过程,整个过程,我们都完全没有想过这个函数到底有什么特性(domain/range/monotonicity/even or ood)等等。
我们也不需要知道它的exact value。这虽然给人一种“不求甚解”的假想,但AMC题目大多就像这道题一样,最重要的就是要最快速的解决问题,有些时候太过于纠结数学题目的传统解决方式,反而是某些大牛同学没能取得好成绩的原因。
以上就是AMC12题目的特点和解题思路了,当然仅仅了解这些还是不够的,要想成功拿下AMC12还是要多做题多练习!