2021年澳大利亚数学思维挑战活动3—4年级学生考前必看知识点！

知己知彼！查缺补漏！养成精准高效的学习方法！方能在克服难题的道路上愈走愈远！

1、计算

一、乘、除法混合运算的本质

商不变性质：被除数和除数乘（或除）以同一个非零数，其商不变。

即：a÷b=(a×n)÷(b×n)=(a÷m)÷(b÷m)

m≠0,n≠0

在连除时，可以交换除数的位置，商不变。

即：a÷b÷c=a÷c÷b

除法运算律：a÷c±b÷c=(a±b)÷c

在乘、除混合运算中，被乘数、乘数或除数可以连同运算符号一起交换位置（即带着符号搬家）。

例如：a×b÷c=a÷c×b=b÷c×a

在乘、除混合运算中，去掉或添加括号的规则。

去括号情形：

（1） 括号前是“×”时，去掉括号后，括号内的乘、除号不变。

即：a×(b×c)=a×b×ca×(b÷c)=a×b÷c

（2） 括号前是“÷”时，去括号后，括号内的“×”变成“÷”，“÷”变成“×”。

即：a÷(b×c)=a÷b÷ca÷(b÷c)=a÷b×c

添加括号情形：

（1）括号前是“×”时，

加括号时，括号内的乘、除号不变。

即：a×b×c=a×(b×c)a×b÷c=a×(b÷c)

（2）括号前是“÷”时，

加括号时，括号内的“×”变成“÷”，“÷”变成“×”。

即：a÷b÷c=a÷(b×c)a÷b×c=a÷(b÷c)

两个数之积除以两个数之积，可以分别相除后再相乘。

即：(a×b)÷(c×d)=

(a÷c)×(b÷d)=(a÷d)×(b÷c)

二、常用特殊数的乘积

125×8＝1000 25×4＝100 125×3＝375

625×16＝10000 7×11×13＝1001

25×8＝200 125×4＝500 37×3=111

三、其它特殊数的乘积

拉面数（乘“11”），

例如：11×11=121;

89×11=979;

2014×11=22154;

重码数

例如：201620162016=2016×1001001

山顶数

例如：

12345678987654321=111111111×111111111

（“1”的个数最大为 9）

轮转数

例如：1234+2341+3412+4123=

(1+2+3+4)×1111

走马灯数：

142857×1=142857;

142857×2=285714;

142857×3=428571;

142857×4=571428;

142857×5=714285;

142857×6=857142;

142857×7=999999。

缺八数：12345679×9=111111111

四、相关公式

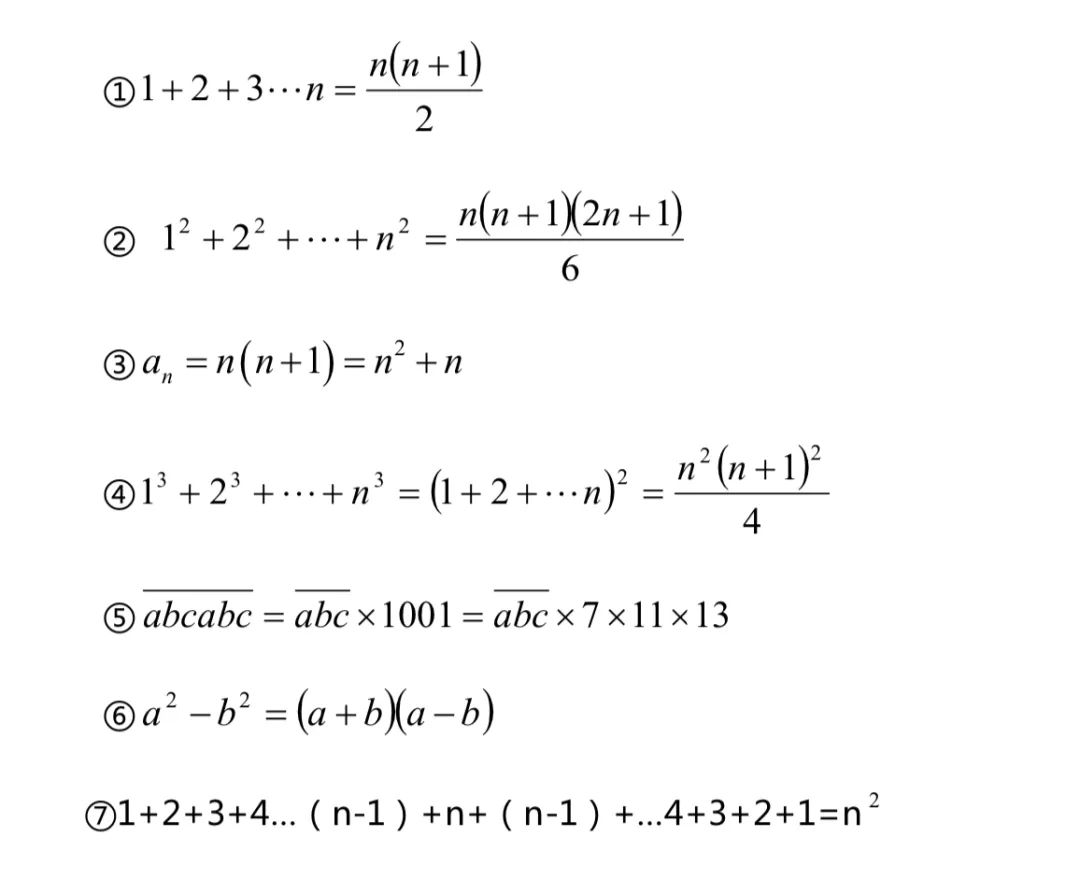
五、数字谜问题

1、一般是指那些含有未知数字或未知运算符号的算式。

这种不完整的算式，就像谜一样，要解开这样的谜，就得根据有关的运算法则、数的性质（和差积商的位数，数的整除性、奇偶性、位数规律等）来进行正确的推理、判断。

2、解数字谜

一般是从某个数的首位或末位数字上寻找突破口。推理时应注意：

1. 数字谜中的文字、字母或其它符号，只取 0-9 中的某个数字；

2. 要认真分析算式中所包含的数量关系，找出尽可能多的隐蔽条件；

3. 必要时应采用枚举和筛选相结合的方法（试验法），逐步淘汰掉那些不符合题意的数字；

4. 数字谜解出之后，最好验算一遍。

2、几何

一、 图形剪拼

即几何操作题，包括：

1、 等分面积；

2、 等分三角形；

3、 分割与拼合；

4、 多边形分割；

注：平面图形分割前后总面积不变。经典三步：算、切、拼。

二、还原问题

方法：箭头表示法

注意：倒推时，加减互逆，乘除互逆。

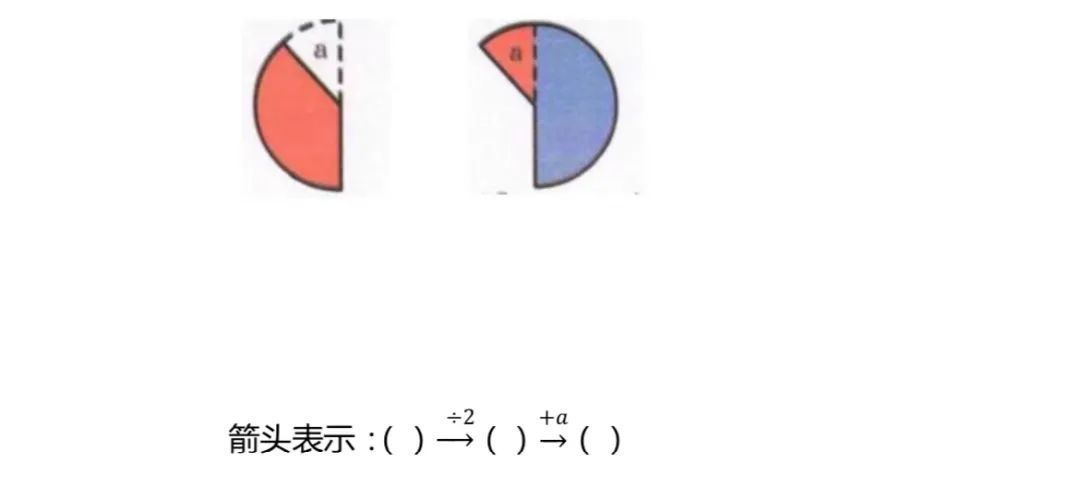
3. 多者还原问题

多组箭头表示（注意：步调一致）

4. 算式出错型

①加法：加数增大‹和增大

②减法：被减数增大‹差增大

减数增大‹差减少

③乘法

④除法

三、对称轴问题

①线段有两条对称轴，是这条线段的垂直平分线和线段所在的直线。

②角有一条对称轴，是角平分线所在的直线。

③等腰三角形有一条对称轴，是顶角平分线所在的直线。

④等边三角形有三条对称轴，分别是三个顶角平分线所在的直线。

⑤矩形有两条对称轴，是相邻两边的垂直平分线。

⑥正方形有四条对称轴，是相邻两边的垂直平分线和对角线所在的直线。

⑦菱形有两条对称轴，是对角线所在的直线。

⑧等腰梯形有一条对称轴，是两底垂直平分线。

⑨正多边形有与边数相同条的对称轴。

⑩圆有无数条对称轴，是任何一条直径所在的直线

四、几何面积知识点

1、基本思路：

在一些面积的计算上，不能直接运用公式的情况下，一般需要对图形进行割补，平移、旋转、翻折、分解、变形、重叠等，使不规则的图形变为规则的图形进行计算;另外需要掌握和记忆一些常规的面积规律。

2、常用方法：

a. 连辅助线方法

b. 利用等底等高的两个三角形面积相等。

c. 大胆假设(有些点的设置题目中说的是任意点，解题时可把任意点设置在特殊位置上)。

d. 利用特殊规律

①等腰直角三角形，已知任意一条边都可求出面积。(斜边的平方除以 4 等于等腰直角三角形的面积)

②梯形对角线连线后，两腰部分面积相等。

③圆的面积占外接正方形面积的 78.5%。

3、基础公式

1）长方形的周长=(长+宽)×2C=(a+b)×2

2）正方形的周长=边长×4C=4a

3）长方形的面积=长×宽 S=ab

4）正方形的面积=边长×边长 S=a*a=a2

5）三角形的面积=底×高÷2S=ah÷2

6）平行四边形的面积=底×高 S=ah

7）梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2

8）直径=半径×2d=2r 半径=直径÷2r=d÷2

9） 圆的周长=

圆周率×直径=圆周率×半径×2c=πd=2πr

10）圆的面积=圆周率×半径×半径

3、数论

一、整除初步

1、若整数 a 除以非零整数 b，商为整数，且余数为零，我们就说 a 能被 b 整除（或说 b 能整除 a），记 b|a，读作“b 整除 a”或“a 能被 b 整除”。

2、能被 2、3、5、9 整除数的特征

1）.能被 2 整除的数的特征：个位上是 0、2、4、6、8 的数都能被 2 整除。

（1） 能被 2 整除数叫做偶数；不能被 2 整除的数叫做奇数。

（2） 奇数±奇数=偶数；偶数±偶数=偶数；

（3） 奇数±偶数=奇数；偶数±奇数=奇数。

（4） 多个数相加（减）时，奇数个奇数之和（差）还是奇数。

2）.能被 3 整除数的特征：一个数的各个数位上的数字的和能被 3 整除，这个数就能被 3 整除。

被 3 整除数的特征的位值原理证明：

假设一个任意的四位数¯a¯b¯c¯d¯，它可以表示为：

¯a¯b¯c¯d¯ = 1000a + 100b+ 10c+ d

= 999a + a + 99b + b + 9c + c + d

= 999a + 99b + 9c + a + b + c + d

= (999a + 99b + 9c) + (a + b + c + d).

因为 3|999a+99b+9c，所以只要 3| a+b+c+d 即可，即上述定义。

注：能被 3 整除的数还可以用“弃 3 法”进行判断：如果该数中有 3 或者 3 的倍数的数全部弃掉，最后如果所有的数字能全部弃掉，则该数可以被 3 整除。

3）.能被 5 整除数的特征：个位上是 0 或 5 的数都能被 5 整除。

能被 5 整除数的特征的位值原理证明：

假设一个任意的四位数¯a¯b¯c¯d¯，

它可以表示为：¯a¯b¯c¯d¯=1000a+100b+10c+d

因为 5|1000a+100b+10c，所以只要5|d 就可以了，即上述定义。

4.）能被 9 整除数的特征：一个数的各个数位上的数字的和能被 9 整除，这个数就能被 9整除。

被 9 整除数的特征的位值原理证明：

假设一个任意的四位数¯a¯b¯c¯d¯，它可以表示为：

¯a¯b¯c¯d¯ = 1000a + 100b+ 10c+ d

= 999a + a + 99b + b + 9c + c + d

= 999a + 99b + 9c + a + b + c + d

= (999a + 99b + 9c) + (a + b + c + d).

因为 9|999a+99b+9c，所以只要 9| a+b+c+d 即可，即上述定义。

注：能被 9 整除的数还可以用“弃 9 法”进行判断：如果该数中有 9 或者 9 的倍数的数全部弃掉，最后如果所有的数字能全部弃掉，则该数可以被 9 整除。

3、2、3、5 整除的综合应用

1. 能同时被 2、5 整除的数的特征：个位上必须是 0.

2. 能同时被 2、3 整除的数的特征：偶数，且数字和是 3 的倍数。

3. 能同时被 3、5 整除的数的特征：个位为 0 或 5，且数字和是 3 的倍数。

4. 能同时被 2、3、5 整除的数的特征：首先个位上必须是 0，其次这个数的各个数位上的数字的和能被 3 整除。

二、“奇偶分析法”

常用知识：

1、奇数表示：2n+1 或 2n-1

2、偶数表示：2n

3、加减法（加减同性）：

偶数+偶数=偶数；奇数+奇数=偶数；偶数+奇数=奇数；

4、乘除法：

偶数×奇数=偶数

（推广开来还可以得到：偶数个奇数相加得偶数）

偶数×偶数=偶数

（推广开就是：偶数个偶数相加得偶数）

奇数×奇数=奇数

（推广开就是：奇数个奇数相加得奇数）

5、任何一个奇数一定不等于任何一个偶数。

三、至多至少问题

至少：就是取满足条件中所有数的最小值.这句话有两个意思,第一,在指定集合范围内,必须都满足要求,第二,指定集合存在最小值.

例如,已经-x²≤a 在所有实数都成立,那么 a 的最小值是多少.

第一,先求出满足-x²≤a 所有 a 的值,显然只要 a≥0,

第二,a=0 是这个集合的最小值,所以 a 的最小值是 0. 两个条件之中有一个不满足,就没有最小值。

至多：就是取满足条件中所有数的最大值.

这句话也有两个意思,第一,在指定集合范围内,必须都满足要求,第二,指定集合存在最大值.

四、同余定理

①同余定义：若两个整数 a，b 被自然数 m 除有相同的余数，那么称 a，b 对于模 m 同余， 用式子表示为a≡b(mod m)

②若两个数 a，b 除以同一个数 c 得到的余数相同，则 a，b 的差一定能被 c 整除。

③两数的和除以 m 的余数等于这两个数分别除以 m 的余数和。

④两数的差除以 m 的余数等于这两个数分别除以 m 的余数差。

⑤两数的积除以 m 的余数等于这两个数分别除以 m 的余数积。

五、100 内质数

2 3 5 7 11 13 17 19 23 29 31 37 41

43 47 53 59 61 67 71 73 79 83 89 97

4、组合初步

一、解排列组合问题

首先要弄清一件事是"分类"还是"分步"完成,对于元素之间的关系,还要考虑"是有序"的还是"无序的",也就是会正确使用分类计数原理和分步计数原理,排列定义和组合定义,其次,对一些复杂的带有附加条件的问题,需掌握以下几种常用的解题方法:

1、特殊优先法

对于存在特殊元素或者特殊位置的排列组合问题,我们可以从这些特殊的东西入手,先解决特殊元素或特殊位置,再去解决其它元素或位置,这种解法叫做特殊优先法.

例如:用 0,1,2,3,4 这5个数字,组成没有重复数字的三位数,其中偶数共有  -___个.(答案:30个)

2、科学分类法

对于较复杂的排列组合问题,由于情况繁多,因此要对各种不同情况,进行科学分类,以便有条不紊地进行解答,避免重复或遗漏现象发生

例如:从 6 台原装计算机和 5 台组装计算机中任取5 台,其中至少有原装与组装计算机各两台,则不同的选取法有___种.(答案:350)

3、插空法

解决一些不相邻问题时,可以先排一些元素然后插入其余元素,使问题得以解决

例如:7 人站成一行,如果甲乙两人不相邻,则不同排法种数是___.(答案:3600)

捆绑法相邻元素的排列,可以采用"整体到局部"的排法,即将相邻的元素当成"一个"元素进行排列,然后再局部排列

例如:6 名同学坐成一排,其中甲,乙必须坐在一起的不同坐法是___种.(答案:240)

4、排除法 

从总体中排除不符合条件的方法数,这是一种间接解题的方法.

二、其他解题方法

1、分类加法计数原理

完成一件事，有 n 类办法，在第 1 类办法中有 m1 种不同的方法，在第 2 类办法中有 m2 种不同的方法‥‥‥则总共有 m1+m2+…+mn 种方法。

2、枚举法

在进行归纳推理时，如果逐个考察了某类事件的所有可能情况，因而得出一般结论，那么这结论是可靠的，这种归纳方法叫做枚举法。

采用枚举算法解题的基本思路：

（1）确定枚举对象、枚举范围和判定条件；

（2）枚举可能的解，验证是否是问题的解。

三、解题原理

1、加法原理：分类枚举

2、乘法原理：排列组合

3、容斥原理：

总数量=A+B+C-(AB+AC+BC)+ABC

常用：总数量=A+B-AB

5、单位换算

1 米=3 尺=3.2808 英尺=1.0926 码

1 公里=1000 米=2 里

1 码=3 英尺=36 英 寸

1 海里=1852 米=3.704 里=1.15 英里

1 平方公里=1000000 平方米=100 公顷 =4 平方里=0.3861 平方英里

1 平方米=100 平方分米=10000 平方厘米

1 公顷=100 公亩=15 亩=2.4711 英亩

1 立方米=1000 立方分米=1000000 立方厘米

1 立方米=27 立方尺=1.308 立方码=35.3147 立方英尺

1 吨=1000 公斤=1000 千 克

1 公斤=1000 克=2 斤（市制）=2.2046 磅