【全网首发】2021USAJMO 真题及答案

【全网首发】2021USAJMO 真题及答案

文末有答案

Problem 1

Let  denote the set of positive integers. Find all functions  such that for positive integers  and 

Problem 2

Rectangles   and  are erected outside an acute triangle  Suppose thatProve that lines   and  are concurrent.

Problem 3

An equilateral triangle  of side length  is given. Suppose that  equilateral triangles with side length 1 and with non-overlapping interiors are drawn inside , such that each unit equilateral triangle has sides parallel to , but with opposite orientation. (An example with  is drawn below.)Prove that

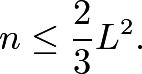
Problem 4

Carina has three pins, labeled , and , respectively, located at the origin of the coordinate plane. In a move, Carina may move a pin to an adjacent lattice point at distance  away. What is the least number of moves that Carina can make in order for triangle  to have area 2021?

(A lattice point is a point  in the coordinate plane where  and  are both integers, not necessarily positive.)

 

Problem 5

A finite set  of positive integers has the property that, for each  and each positive integer divisor  of , there exists a unique element  satisfying . (The elements  and  could be equal.)

Given this information, find all possible values for the number of elements of .

Problem 6

Let  be an integer. Find all positive real solutions to the following system of  equations: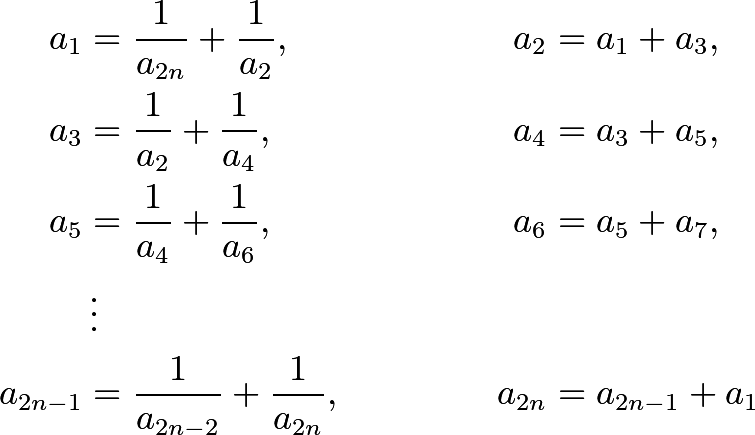

Problem 1

Solution

I claim that the only function  that satisfies the constraints outlined within the problem is the function  for all positive integers .

We will proceed with strong induction. The base case is simple, as plugging  into the second equation given within the problem gives . Since  can only return a positive integer value, we have that .

Now we proceed with the inductive step. If the next number  is either a perfect square or can be represented as a sum of two perfect squares, then obviously , as it is either the product of two -values that are both equal to  from the inductive assumption or is the square of an -value that is equal to , again due to the inductive assumption. Otherwise, we can use the Sum of Two Squares Theorem, which tells us that has at least one prime in its prime factorization that is  and is raised to an odd power.

Lemma 1: Given that  and , we then have .

Proof: Note that the first condition in the problem tells us that , or . Using the second condition gives us . Plugging in the values of  and  gives us that .

Now we will attempt to repeatedly remove prime factors that are  and taken to an odd power, and we will move from the largest prime down to the smallest prime that satisfies above conditions. The prime factors will be removed by constructing a Pythagorean Triple with the prime being the smallest leg in the form of 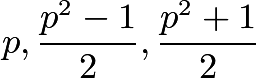(this will always work as (not 3 mod 4), and this method works via Lemma 1). We will then prove the ending numbers that we achieve via removing all the  primes(which I will refer to as "tips") are equal to 1 b/c they can be expressed as the sum of two squares or is a perfect square(Sum of Two Squares Theorem). For example, if we took the number , we would first aim to remove the  by splitting it into  and , so  would become  and .  is divisible by  to an odd power, so we transform it into  and . These two don't have any divisors that are  raised to an odd power so we leave it alone, as sum of two squares will work on them or they are perfect squares.  does have a prime factor that is , but it is an even power so we leave it alone. In this case, the tips are , , and . However, now we need to prove two key facts: using this Pythagorean Triple Method will never generate another  prime that is bigger than the current one we are working on or create more primes or keep the same number of primes in the tips' prime factorizations., as otherwise it could cause an infinite cycle, and also we must prove when we use Sum of Two Squares/Perfect Square given in the second condition on the tips the square root of the square(s) used will never be greater than or equal to .

The first claim can be proved rather simply. Note that 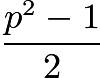 can have no prime factors greater than or equal to , as it can be factored as 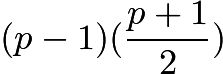, which are both less than  and are integers( must be an integer due to  must being odd(not equal to )). For 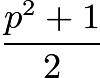, we can prove something a bit more general.

Lemma 2: For any positive integer , all prime factors of  must be .

Proof: Note that if , then we also must have , or . Now we can apply Fermat's Little Theorem to obtain . Note that since  and  are obviously not , as , we have that  is a multiple of , or .

We can simply apply Lemma 2 to  as  is obviously not , and this means that a prime factor  will never be generated from this term. This completes the first of our two claims.

Now we proceed to the second of our two claims. Note that every time we use the method on  based on prime , we will multiply by around , clearly less than (if we multiply by  we would get  which is clearly greater than 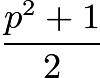). We will never have to use the same prime twice in our method, so at max in the end we will multiply  by the product of a little less than all  primes that divide it, which is less than itself for  greater than or equal to (the smallest 3 mod 4 prime), meaning that the largest number that we must use two squares on that is generated by out method is less than . We need to prove that the two squares that sum to this are both less than , which is quite trivial, as they are less than , which obviously means it must be less than . This proves the second of our claims.

This completes the second case of the inductive step, and therefore completes both the induction and the problem. ~Solution by hyxue

Solution 2 (Taken from Twitch Solves ISL)

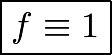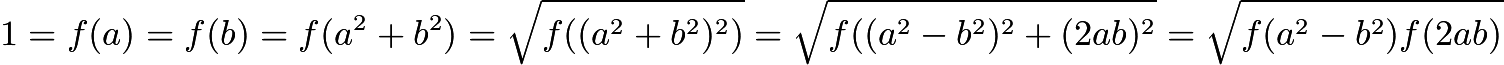The Answer is  which works but we want to prove that it's the only one. Claim: If  and a>b, then . Proof: We can write . We set it to  and we get that . Easily by Induction it shows f(n)=1. We take if  take  which . If , just take  which . Thus the only answer is 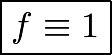 and we are done.

Solution 3 (clear Solution 2)

The answer is 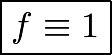, which works. To show it is necessary, we first get , so . Then, we get .

The following claim finishes the problem via induction:

Claim: If  for , we have .

Proof: Note that , soimplies .

Note that , soimplies . 

Thus, the only solution is .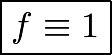

Problem 2

Solution

We first claim that the three circles   and  share a common intersection.

Let the second intersection of  and  be . Then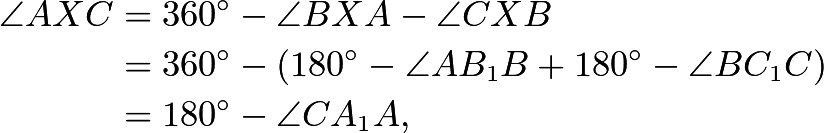which implies that  is cyclic as desired.

Now we show that  is the intersection of   and  Note that  so  are collinear. Similarly,  and  are collinear, so the three lines concur and we are done.

Problem 4

Solution 1

The answer is , achievable by . We now show the bound.

We first do the following optimizations:

-if you have a point goes both left and right, we may obviously delete both of these moves and decrease the number of moves by .

-if all of  lie on one side of the plane, for example , we shift them all down, decreasing the number of moves by , until one of the points is on  for the first time.

Now we may assume that , ,  where . Note we may still shift all  down by  if , decreasing the number of moves by , until one of  is on  for the first time. So we may assume one of  and  is , by symmetry. In particular, by shoelace the answer to 2021 JMO Problem 4 is the minimum of the answers to the following problems:

Case 1 (where ) if , find the minimum possible value of .

Case 2 (else) , find the minimum possible value of .

Note that  so if  is fixed then  is maximized exactly when  is minimized. In particular, if  then  as desired.