AP微积分丨敲黑板，这些知识点很重要

AP微积分

AP是The Advanced Placement Program的缩写，即大学预修课程，指由college board提供的在高中授课的大学课程。由于美国大学把学生在AP考试中的表现作为衡量其是否能够胜任大学学习的依据之一，选修AP课程和通过AP考试不仅是对学生能力和学业水平的证明，而且会令学生在申请大学时具有很大的优势，尤其体现在顶尖大学的申请中。

进入大学后，又可以免修同类课程(各学校有转换学时的具体规定)，提早选修更高级的课程，节省学费的同时提早毕业。在顶尖大学，4分以上或者5分可以换取相应学时；在前50的大学，4分就可以换取相应学时。AP微积分是历年AP考试中报考人数最多的一门课程，其知识深度和知识结构相当于美国大学一年级的微积分课程，是所有AP科目中语言对其影响最小的课程，也是5分率比较高的科目。

在诸多大学热门专业中，如金融学、计算机科学、生命科学、社会学及工程学等，微积分都是必修课程。AP微积分分为AB 和BC两门课程，BC的内容和难度都高于AB的考试，AB 的内容大概占BC内容的70%。鉴于微积分在大学教育中的重要地位，建议数学基础较好的或准备申请理工类的学生考BC，非理工类的学生如果数学基础一般就可报考AB。

AP微积分BC学习的核心内容是函数的极限、导数、积分和无穷级数四部分。其中，导数和积分是重点，无穷级数是难点。AB与BC比较而言，不涉及无穷级数、参数方程、极坐标方程、曲线运动以及部分不定积分的计算方法。试题则主要考察知识的理解、基本运算技能以及概念的基本应用。考试分为两部分：选择题和问答题。具体分配如下：

考试中使用的计算器必须具备以下功能：·在任意大小的窗口画函数图像·找函数零点（数值求解方程）

·计算函数在某一点的导数

·计算函数的积分值
 
在完成第二部分Free Response题目时，需要注意以下问题：

·方法和答案的正确性及完整性。没有给出数学依据的答案是得不到相应分数的。

·解题过程中要使用标准数学符号，而不是计算器语言。

·除非另有说明，答案（数字或代数）不需要简化，小数应精确到小数点后三位。

·除非另有说明，函数的定义域被假定为所有实数的集合。
 
一般情况，AP微积分考试正确率在65%以上可确保5分。每年AP微积分的5分线会有小幅波动，但最高也没有超过70分（满分108分）。从2017年全球和中国考生的成绩来看，虽然BC比AB的学习内容要多，但BC的5分率要高出不少。因此，对于数学基础较好的学生，推荐大家选择BC。
 2017年AP微积分考试得分情况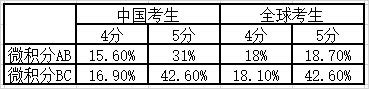

AP微积分考点总结

A. 函数

(1) 函数的定义和性质(定义域值域、单调性、奇偶性和周期性等)

(2) 五种基本初等函数(幂函数、指数、对数、三角和反三角函数的运算公式和函数性质及图像)

(3) 复合函数，反函数

(4) 函数图像平移和变换
*(5) 参数函数，极坐标函数，分段函数

B. 极限和连续

(1) 极限的定义和左右极限

(2) 极限的运算法则和有理函数求极限

(3) 两个重要的极限

(4) 极限的应用-求函数渐近线

(5) 连续的定义

(6) 三类不连续点(移点、跳点和无穷点)

(7) 最值定理、介值定理和零值定理

C. 导数

(1) 导数的定义、几何意义和单侧导数

(2) 极限、连续和可导的关系

(3) 导数的求导法则

(4) 复合函数、反函数、隐函数的求导

(5) 高阶导数

*(6) 参数函数求导数和极坐标求导数

D. 导数的应用

(1) 几何应用-切线和法线和相对变化率

(2) 物理应用-求速度和加速度(一维和二维运动)

(3) 微分中值定理

(4) 求极值、最值，函数的增减性和凹凸性

(5) 洛比达法则求极限

(6) 微分定义及线性估计

(7) 欧拉法则求近似值

E. 不定积分

(1) 不定积分和导数的关系

(2) 不定积分的公式

(3) U换元法求不定积分

*(4) 分部积分法求不定积分

*(5) 分式拆分求不定积分

F. 定积分

(1) 黎曼和的极限及定积分的定义与几何意义

(2) 定积分的性质

*(3) 累计函数求导数

*(4) 反常函数求积分

G. 定积分的应用

(1) 积分中值定理

(2) 定积分求面积、体积

(3) 曲线长度

(4) 定积分的物理应用

H. 微分方程

(1) 可分离变量的微分方程和逻辑斯特微分方程

(2) 斜率场

*I. 无穷级数

(1) 无穷级数的定义和数列的级数

(2) 三种审敛法：比值、积分和比较审敛法

(3) 四种级数：调和级数、几何级数、P级数和交错级数

(4) 幂级数(收敛半径)、泰勒级数和麦克劳林级数

(5) 级数的运算和拉格朗日误差（限）