AP Statistics | Unit 6 Random Variable (下)

大家好呀今天我们来看Random Variable单元的下半部分（以及被催稿之下的人们的脑回路是怎样的)

这次的内容摘要-Binomial Random Variables-Binomial Distribution-Binomial Formula-Mean and standard deviation-Geometric Random Variables-Geometric Distribution-Mean of geometric distribution

-Normal Conditions

Binomial Setting二项随机变数的特点其实可以概括成“BINS”，也就是Binary：只有两种结果（outcome）——就是success和failure

Independent：是独立事件，trial和trial之间的结果不能互相影响。

Number of Trials：trials的次数一定是固定的。注意，这个是binomial和geometric的主要区别之一！

S(success)：success的几率(probability)

Binomial event的举例：

现在我有一大袋彩虹糖，想知道里面有多少黄色的，于是我打算总共从里面SRS二十颗(fixed number of trials)，with replacement，分为是黄色(success)和不是黄色 (failure)两种结果。最后，二十颗里有10颗是黄色，于是success(S)的几率就是0.5。

接着，我重复这个过程很多很多次，每次的结果都记录在一个graph上，就变成了这个事件的Binomial Distribution，可以表示为Bin (n, p)，n为number of trials，p是success的几率。

再来，就是比较重点的计算部分了，值得开心的是，统计的计算看似复杂，但是在计算器的帮助下根本不算个事儿：这里就直接举例子了！

掷筛子5次，求得到一次数字4的几率是多少：

这时候可以再TI-Nspire里输入binopdf(5, 1/6, 1)，这三个数字分别代表刚才提到过的n，p，而1便是出现这个结果的次数。

而用这种方法直接算得到的结果也是一样的，可以说会更直观：(见图)

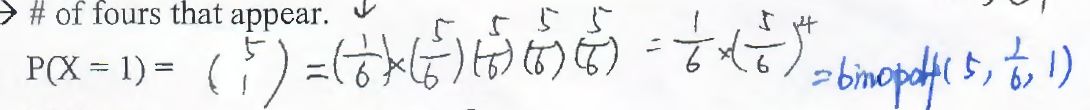还有，Check you FORMULA SHEET!!!

遇到题的时候你才会发现formula sheet到底多么值得珍惜。

Mean and Standard Deviation 不哆说啊，直接套公式：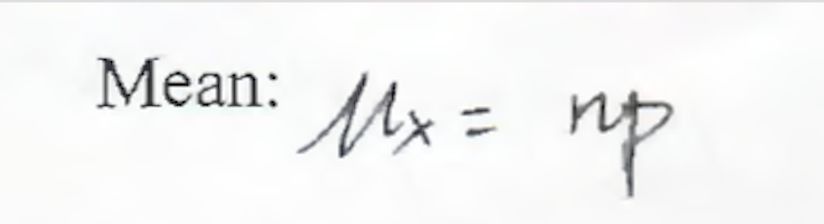 

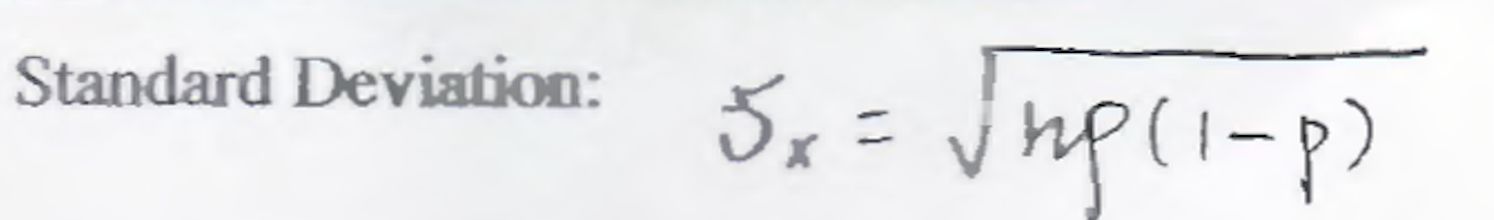
Geometric Setting  Geometric Distribution跟BINS不一样，geometric setting是BITS：

Binary一样：只有success或failure两种结果

Independent一样：是独立事件，trial和trial之间的结果不能互相影响。

Trials: 很不一样！你只需要一直重复，直到出现第一次success就可以了。可以把geometric理解成累计的感觉。与Binomial的其他不同点-用p表示，没有固定的n(number of trials)

-跟binomial distribution不一样，不包括0次，因为至少要有1次才能出现success的情况。
-always skewed to the right（大部分聚集在左边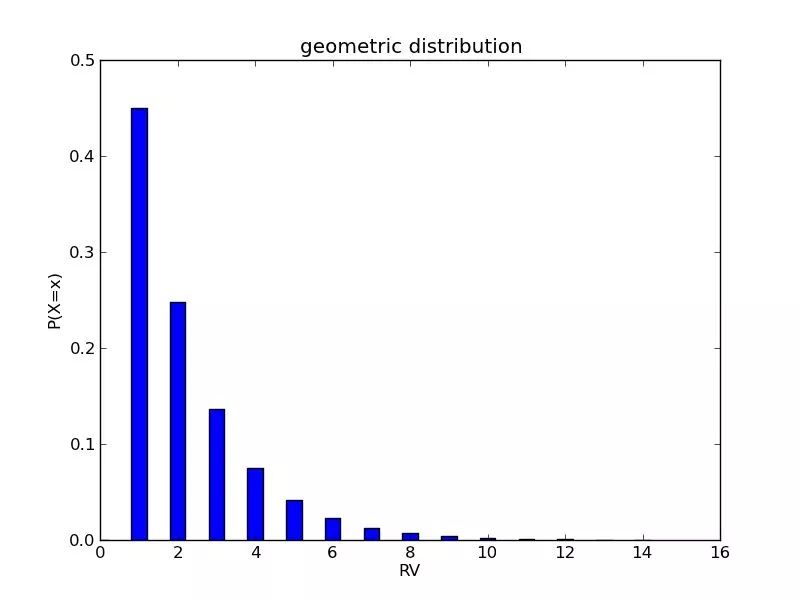）  Mean of geometric Distribution  p的倒数，也就是1/p。

Normal Conditions最后，既然geometric distribution是skewed right，那么binomial呢？是normal吗？

不一定。上述binomial的那两条formula，其实是要在试验次数够大的时候才能用的，不然结果会很不准确进而产生bias。那何时才能用此神技？

如果np>10, 并且n(1-p)>10，

你就可以用normal approximation了，也就是直接假设这个distribution是normal的。 那么,到此为止，

AP Statistics的内容你已经学了一半了

对5月份的考试有信心吗？

一般，没有才是正常的，

所以继续努力吧

纸质版笔记的链接：

https://pan.baidu.com/s/1cEtvVS  密码：gpqz