Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2020 AIME I真题及答案高清文字版

Category: AMC美国数学竞赛, 国际竞赛, 数学国际竞赛 Date: 2020年7月30日下午12:59

2020 AIME I真题及答案

参考答案见文末（仅供参考）

Problem 1

In $\triangle ABC$ with $AB=AC,$ point $D$ lies strictly between $A$ and $C$ on side $\overline{AC},$ and point $E$ lies strictly between $A$ and $B$ on side $\overline{AB}$ such that $AE=ED=DB=BC.$ The degree measure of $\angle ABC$ is $\tfrac{m}{n},$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Problem 2

There is a unique positive real number $x$ such that the three numbers $\log_8{2x}$ , $\log_4{x}$ , and $\log_2{x}$ , in that order, form a geometric progression with positive common ratio. The number $x$ can be written as $\frac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find $m + n$ .

Problem 3

A positive integer $N$ has base-eleven representation $\underline{a}\kern 0.1em\underline{b}\kern 0.1em\underline{c}$ and base-eight representation $\underline1\kern 0.1em\underline{b}\kern 0.1em\underline{c}\kern 0.1em\underline{a},$ where $a,b,$ and $c$ represent (not necessarily distinct) digits. Find the least such $N$ expressed in base ten.

Problem 4

Let $S$ be the set of positive integers $N$ with the property that the last four digits of $N$ are $2020,$ and when the last four digits are removed, the result is a divisor of $N.$ For example, $42,020$ is in $S$ because $4$ is a divisor of $42,020.$ Find the sum of all the digits of all the numbers in $S.$ For example, the number $42,020$ contributes $4+2+0+2+0=8$ to this total.

Problem 5

Six cards numbered $1$ through $6$ are to be lined up in a row. Find the number of arrangements of these six cards where one of the cards can be removed leaving the remaining five cards in either ascending or descending order.

Problem 6

A flat board has a circular hole with radius $1$ and a circular hole with radius $2$ such that the distance between the centers of the two holes is $7.$ Two spheres with equal radii sit in the two holes such that the spheres are tangent to each other. The square of the radius of the spheres is $\tfrac{m}{n},$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Problem 7

A club consisting of $11$ men and $12$ women needs to choose a committee from among its members so that the number of women on the committee is one more than the number of men on the committee. The committee could have as few as $1$ member or as many as $23$ members. Let $N$ be the number of such committees that can be formed. Find the sum of the prime numbers that divide $N.$

Problem 8

A bug walks all day and sleeps all night. On the first day, it starts at point $O,$ faces east, and walks a distance of $5$ units due east. Each night the bug rotates $60^\circ$ counterclockwise. Each day it walks in this new direction half as far as it walked the previous day. The bug gets arbitrarily close to the point $P.$ Then $OP^2=\tfrac{m}{n},$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Problem 9

Let $S$ be the set of positive integer divisors of $20^9.$ Three numbers are chosen independently and at random with replacement from the set $S$ and labeled $a_1,a_2,$ and $a_3$ in the order they are chosen. The probability that both $a_1$ divides $a_2$ and $a_2$ divides $a_3$ is $\tfrac{m}{n},$ where $m$ and $n$ are relatively prime positive integers. Find $m.$

Problem 10

Let $m$ and $n$ be positive integers satisfying the conditions

$\quad\bullet\ \gcd(m+n,210)=1,$

$\quad\bullet\ m^m$ is a multiple of $n^n,$ and

$\quad\bullet\ m$ is not a multiple of $n.$

Find the least possible value of $m+n.$

Problem 11

For integers $a,b,c$ and $d,$ let $f(x)=x^2+ax+b$ and $g(x)=x^2+cx+d.$ Find the number of ordered triples $(a,b,c)$ of integers with absolute values not exceeding $10$ for which there is an integer $d$ such that $g(f(2))=g(f(4))=0.$

Problem 12

Let $n$ be the least positive integer for which $149^n-2^n$ is divisible by $3^3\cdot5^5\cdot7^7.$ Find the number of positive integer divisors of $n.$

Problem 13

Point $D$ lies on side $\overline{BC}$ of $\triangle ABC$ so that $\overline{AD}$ bisects $\angle BAC.$ The perpendicular bisector of $\overline{AD}$ intersects the bisectors of $\angle ABC$ and $\angle ACB$ in points $E$ and $F,$ respectively. Given that $AB=4,BC=5,$ and $CA=6,$ the area of $\triangle AEF$ can be written as $\tfrac{m\sqrt{n}}p,$ where $m$ and $p$ are relatively prime positive integers, and $n$ is a positive integer not divisible by the square of any prime. Find $m+n+p.$

Problem 14

Let $P(x)$ be a quadratic polynomial with complex coefficients whose $x^2$ coefficient is $1.$ Suppose the equation $P(P(x))=0$ has four distinct solutions, $x=3,4,a,b.$ Find the sum of all possible values of $(a+b)^2.$

Problem 15

Let $\triangle ABC$ be an acute triangle with circumcircle $\omega,$ and let $H$ be the intersection of the altitudes of $\triangle ABC.$ Suppose the tangent to the circumcircle of $\triangle HBC$ at $H$ intersects $\omega$ at points $X$ and $Y$ with $HA=3,HX=2,$ and $HY=6.$ The area of $\triangle ABC$ can be written as $m\sqrt{n},$ where $m$ and $n$ are positive integers, and $n$ is not divisible by the square of any prime. Find $m+n.$

参考答案及详解注册后登录可见：

Solution 1

$[asy] size(10cm); pair A, B, C, D, F; A = (0, tan(3 * pi / 7)); B = (1, 0); C = (-1, 0); F = rotate(90/7, A) * (A - (0, 2)); D = rotate(900/7, F) * A; draw(A -- B -- C -- cycle); draw(F -- D); draw(D -- B); label("$A$", A, N); label("$B$", B, E); label("$C$", C, W); label("$D$", D, W); label("$E$", F, E); [/asy]$

If we set $\angle{BAC}$ to $x$ , we can find all other angles through these two properties: 1. Angles in a triangle sum to $180^{\circ}$ . 2. The base angles of an isosceles triangle are congruent.

Now we angle chase. $\angle{ADE}=\angle{EAD}=x$ , $\angle{AED} = 180-2x$ , $\angle{BED}=\angle{EBD}=2x$ , $\angle{EDB} = 180-4x$ , $\angle{BDC} = \angle{BCD} = 3x$ , $\angle{CBD} = 180-6x$ . Since $AB = AC$ as given by the problem, $\angle{ABC} = \angle{ACB}$ , so $180-4x=3x$ . Therefore, $x = 180/7^{\circ}$ , and our desired angle is $180-4\left(\frac{180}{7}\right) = \frac{540}{7}$ for an answer of $\boxed{547}$ .

Solution 2

Let $\angle{BAC}$ be $x$ in degrees. $\angle{ADE}=x$ . By Exterior Angle Theorem on triangle $AED$ , $\angle{BED}=2x$ . By Exterior Angle Theorem on triangle $ADB$ , $\angle{BDC}=3x$ . This tells us $\angle{BCA}=\angle{ABC}=3x$ and $3x+3x+x=180$ . Thus $x=\frac{180}{7}$ and we want $\angle{ABC}=3x=\frac{540}{7}$ to get an answer of $\boxed{547}$ .

Solution 3 (Official MAA)

Let $x = \angle ABC = \angle ACB$ . Because $\triangle BCD$ is isosceles, $\angle CBD = 180^\circ - 2x$ . Then $\angle DBE = x - \angle CBD = x - (180^\circ - 2x) = 3x - 180^\circ\!.$ Because $\triangle EDA$ and $\triangle DBE$ are also isosceles, $\angle BAC =\frac12(\angle EAD + \angle ADE) = \frac12(\angle BED)= \frac12(\angle DBE)$ $= \frac12 (3x - 180^\circ) = \frac32x-90^\circ\!.$ Because $\triangle ABC$ is isosceles, $\angle BAC$ is also $180^\circ-2x$ , so $\frac32x - 90^\circ = 180^\circ - 2x$ , and it follows that $\angle ABC = x = \left(\frac{540}7\right)^\circ$ . The requested sum is $540+7 = 547$ .

$[asy] unitsize(4 cm); pair A, B, C, D, E; real a = 180/7; A = (0,0); B = dir(180 - a/2); C = dir(180 + a/2); D = extension(B, B + dir(270 + a), A, C); E = extension(D, D + dir(90 - 2*a), A, B); draw(A--B--C--cycle); draw(B--D--E); label("$A$", A, dir(0)); label("$B$", B, NW); label("$C$", C, SW); label("$D$", D, S); label("$E$", E, N); [/asy]$

2.Solution1

Since these form a geometric series, $\frac{\log_2{x}}{\log_4{x}}$ is the common ratio. Rewriting this, we get $\frac{\log_x{4}}{\log_x{2}} = \log_2{4} = 2$ by base change formula. Therefore, the common ratio is 2. Now $\frac{\log_4{x}}{\log_8{2x}} = 2 \implies \log_4{x} = 2\log_8{2} + 2\log_8{x} \implies \frac{1}{2}\log_2{x} = \frac{2}{3} + \frac{2}{3}\log_2{x}$

$\implies -\frac{1}{6}\log_2{x} = \frac{2}{3} \implies \log_2{x} = -4 \implies x = \frac{1}{16}$ . Therefore, $1 + 16 = \boxed{017}$ .

Solution 2

If we set $x=2^y$ , we can obtain three terms of a geometric sequence through logarithm properties. The three terms are $\frac{y+1}{3}, \frac{y}{2}, y.$ In a three-term geometric sequence, the middle term squared is equal to the product of the other two terms, so we obtain the following: $\frac{y^2+y}{3} = \frac{y^2}{4},$ which can be solved to reveal $y = -4$ . Therefore, $x = 2^{-4} = \frac{1}{16}$ , so our answer is $\boxed{017}$ .

Solution 3

Let $r$ be the common ratio. We have $r = \frac{\log_4{(x)}}{\log_8{(2x)}} = \frac{\log_2{(x)}}{\log_4{(x)}}$ Hence we obtain $(\log_4{(x)})(\log_4{(x)}) = (\log_8{(2x)})(\log_2{(x)})$ Ideally we change everything to base $64$ and we can get: $(\log_{64}{(x^3)})(\log_{64}{(x^3)}) = (\log_{64}{(x^6)})(\log_{64}{(4x^2)})$ Now divide to get: $\frac{\log_{64}{(x^3)}}{\log_{64}{(4x^2)}} = \frac{\log_{64}{(x^6)}}{\log_{64}{(x^3)}}$ By change-of-base we obtain: $\log_{(4x^2)}{(x^3)} = \log_{(x^3)}{(x^6)} = 2$ Hence $(4x^2)^2 = x^3 \rightarrow 16x^4 = x^3 \rightarrow x = \frac{1}{16}$ and we have $1+16 = \boxed{017}$ as desired.

~skyscraper

Solution 4 (Exponents > Logarithms)

Let $r$ be the common ratio, and let $a$ be the starting term ( $a=\log_{8}{(2x)}$ ). We then have: $\log_{8}{(2x)}=a, \log_{4}{(x)}=ar, \log_{2}{(x)}=ar^2$ Rearranging these equations gives: $8^a=2x, 4^{ar}=x, 2^{ar^2}=x$ Deal with the last two equations first: Setting them equal gives: $4^{ar}=2^{ar^2} \Rightarrow 2^{2ar}=2^{ar^2}$ Using LTE results in: $2ar=ar^2 \Rightarrow r=2$ Using this value of $r$ , substitute into the first and second equations (or the first and third, it doesn't really matter) to get: $8^a=2x, 4^{2a}=x$ Changing these to a common base gives: $2^{3a}=2x, 2^{4a}=x$ Dividing the first equation by 2 on both sides yields: $2^{3a-1}=x$ Setting these equations equal to each other and applying LTE again gives: $3a-1=4a \Rightarrow a=-1$ Substituting this back into the first equation gives: $8^{-1}=2x \Rightarrow 2x=\frac{1}{8} \Rightarrow x=\frac{1}{16}$ Therefore, $m+n=1+16=\boxed{017}$

~IAmTheHazard

Solution 5

We can relate the logarithms as follows:

$\frac{\log_4{x}}{\log_8{(2x)}}=\frac{\log_2{x}}{\log_4{x}}$ $\log_8{(2x)}\log_2{x}=\log_4{x}\log_4{x}$

Now we can convert all logarithm bases to $2$ using the identity $\log_a{b}=\log_{a^c}{b^c}$ :

$\log_2{\sqrt[3]{2x}}\log_2{x}=\log_2{\sqrt{x}}\log_2{\sqrt{x}}$

We can solve for $x$ as follows:

$\frac{1}{3}\log_2{(2x)}\log_2{x}=\frac{1}{4}\log_2{x}\log_2{x}$ $\frac{1}{3}\log_2{(2x)}=\frac{1}{4}\log_2{x}$ $\frac{1}{3}\log_2{2}+\frac{1}{3}\log_2{x}=\frac{1}{4}\log_2{x}$ We get $x=\frac{1}{16}$ . Verifying that the common ratio is positive, we find the answer of $\boxed{017}$ .

~QIDb602

Solution 6

If the numbers are in a geometric sequence, the middle term must be the geometric mean of the surrounding terms. We can rewrite the first two logarithmic expressions as $\frac{1+\log_2{x}}{3}$ and $\frac{1}{2}\log_2{x}$ , respectively. Therefore: $\frac{1}{2}\log_2{x}=\sqrt{\left(\frac{1+\log_2{x}}{3}\right)\left(\log_2{x}\right)}$ Let $n=\log_2{x}$ . We can rewrite the expression as: $\frac{n}{2}=\sqrt{\frac{n(n+1)}{3}}$ $\frac{n^2}{4}=\frac{n(n+1)}{3}$ $4n(n+1)=3n^2$ $4n^2+4n=3n^2$ $n^2+4n=0$ $n(n+4)=0$ $n=0 \text{ and } -4$ Zero does not work in this case, so we consider $n=-4$ : $\log_2{x}=-4 \rightarrow x=\frac{1}{16}$ . Therefore, $1+16=\boxed{017}$ .

~Bowser498

Solution 7 (Official MAA)

By the Change of Base Formula the common ratio of the progression is $\frac{\log_2 x}{\log_4 x} = \frac{\hphantom{m}\log_2x\hphantom{m}}{\frac{\log_2x}{\log_24}} = 2.$ Hence $x$ must satisfy $2=\frac{\log_4 x}{\log_8 (2x)}= \frac{\log_2 x}{\log_2 4} \div \frac{\log_2(2x)}{\log_28} = \frac 32\cdot \frac{\log_2x}{1+\log_2x}.$ This is equivalent to $4 + 4\log_2x = 3\log_2x$ . Hence $\log_2x = -4$ and $x = \frac{1}{16}$ . The requested sum is $1+16 = 17$ .

3.Solution 1

From the given information, $121a+11b+c=512+64b+8c+a \implies 120a=512+53b+7c$ . Since $a$ , $b$ , and $c$ have to be positive, $a \geq 5$ . Since we need to minimize the value of $n$ , we want to minimize $a$ , so we have $a = 5$ . Then we know $88=53b+7c$ , and we can see the only solution is $b=1$ , $c=5$ . Finally, $515_{11} = 621_{10}$ , so our answer is $\boxed{621}$ .

~ JHawk0224

Solution 2 (Official MAA)

The conditions of the problem imply that $121a + 11b + c = 512 + 64b + 8 c + a$ , so $120 a = 512+ 53b+7c$ . The maximum digit in base eight is $7,$ and because $120a \ge 512$ , it must be that $a$ is $5, 6,$ or $7.$ When $a = 5$ , it follows that $600=512 + 53b+7c$ , which implies that $88 = 53b+7c$ . Then $b$ must be $0$ or $1.$ If $b = 0$ , then $c$ is not an integer, and if $b = 1$ , then $7c = 35$ , so $c = 5$ . Thus $N = 515_\text{eleven}$ , and $N=5\cdot 121 + 1\cdot 11 + 5 = 621$ . The number $637_{\rm eleven} =1376_{\rm eight} = 766$ also satisfies the conditions of the problem, but $621$ is the least such number.

4.Solution 1

We note that any number in $S$ can be expressed as $a(10,000) + 2,020$ for some integer $a$ . The problem requires that $a$ divides this number, and since we know $a$ divides $a(10,000)$ , we need that $a$ divides 2020. Each number contributes the sum of the digits of $a$ , as well as $2 + 0 + 2 +0 = 4$ . Since $2020$ can be prime factorized as $2^2 \cdot 5 \cdot 101$ , it has $(2+1)(1+1)(1+1) = 12$ factors. So if we sum all the digits of all possible $a$ values, and add $4 \cdot 12 = 48$ , we obtain the answer.

Now we list out all factors of $2,020$ , or all possible values of $a$ . $1,2,4,5,10,20,101,202,404,505,1010,2020$ . If we add up these digits, we get $45$ , for a final answer of $45+48=\boxed{093}$ .

-molocyxu

Solution 2 (Official MAA)

Suppose that $N$ has the required property. Then there are positive integers $k$ and $m$ such that $N = 10^4m + 2020 = k\cdot m$ . Thus $(k - 10^4)m = 2020$ , which holds exactly when $m$ is a positive divisor of $2020.$ The number $2020 = 2^2\cdot 5\cdot 101$ has $12$ divisors: $1, 2, 4, 5, 10, 20, 101, 202, 404, 505, 1010$ , and $2020.$ The requested sum is therefore the sum of the digits in these divisors plus $12$ times the sum of the digits in $2020,$ which is $(1+2+4+5+1+2+2+4+8+10+2+4)+12\cdot4 = 93.$

5.Solution 1

Realize that any sequence that works (ascending) can be reversed for descending, so we can just take the amount of sequences that satisfy the ascending condition and multiply by two.

If we choose any of the numbers $1$ through $6$ , there are five other spots to put them, so we get $6 \cdot 5 = 30$ . However, we overcount some cases. Take the example of $132456$ . We overcount this case because we can remove the $3$ or the $2$ . Therefore, any cases with two adjacent numbers swapped is overcounted, so we subtract $5$ cases (namely, $213456, 132456, 124356, 123546, 123465$ ,) to get $30-5=25$ , but we have to add back one more for the original case, $123456$ . Therefore, there are $26$ cases. Multiplying by $2$ gives the desired answer, $\boxed{052}$ .

-molocyxu

Solution 2 (Inspired by 2018 CMIMC combo round)

Similar to above, a $1-1$ correspondence between ascending and descending is established by subtracting each number from $7$ .

We note that the given condition is equivalent to "cycling" $123456$ for a contiguous subset of it. For example,

$12(345)6 \rightarrow 125346, 124536$

It's not hard to see that no overcount is possible, and that the cycle is either $1$ "right" or $1$ "left." Therefore, we consider how many elements we flip by. If we flip $1$ or $2$ such elements, then there is one way to cycle them. Otherwise, we have $2$ ways. Therefore, the total number of ascending is $1 + 5 + 2(4 + 3 + 2 + 1) = 26$ , and multiplying by two gives $\boxed{052}.$ ~awang11

Solution 3

Similarly to above, we find the number of ascending arrangements and multiply by 2.

We can choose $5$ cards to be the ascending cards, therefore leaving $6$ places to place the remaining card. There are $\binom{6}{5}\cdot 6=36$ to do this. However, since the problem is asking for the number of arrangements, we overcount cases such as $123456$ . Notice that the only arrangements that overcount are $123456$ (case 1) or if two adjacent numbers of $123456$ are switched (case 2).

$\text{Case 1: }$ This arrangement is counted $6$ times. Each time it is counted for any of the $5$ numbers selected. Therefore we need to subtract $5$ cases of overcounting.

$\text{Case 2: }$ Each time $2$ adjacent numbers of switched, there is one overcount. For example, if we have $213456$ , both $1$ or $2$ could be removed. Since there are $5$ possible switches, we need to subtract $5$ cases of overcounting.

Therefore, we have $36-5-5=26$ total arrangements of ascending numbers. We multiply by two (for descending) to get the answer of $\boxed{052}.$ -PCChess

Solution 4 (No overcounting)

Like in previous solutions, we will count the number of ascending arrangements and multiply by 2.

First, consider the arrangement 1-2-3-4-5-6. That gives us 1 arrangement which works.

Next, we can switch two adjacent cards. There are 5 ways to pick two adjacent cards, so this gives us 5 arrangements.

Now, we can "cycle" 3 adjacent cards. For example, 1-2-3 becomes 2-3-1 which becomes 3-1-2. There are 4 ways to pick a set of 3 adjacent cards, so this gives us 4x2=8 arrangements.

Cycling 4 adjacent cards, we get the new arrangements 2-3-4-1 (which works,) 3-4-1-2 (which doesn't work,) and 4-1-2-3 (which does work.) We get 6 arrangements.

Similarly, when cycling 5 cards, we find 2x2=4 arrangements, and when cycling 6 cards, we find 2x1=2 arrangements.

Adding, we figure out that there are 1+5+8+6+4+2=26 ascending arrangements. Multiplying by 2, we get the answer $\boxed{052}.$ -i8Pie

Solution 5 (Official MAA 1)

First count the number of permutations of the cards such that if one card is removed, the remaining cards will be in ascending order. There is $1$ such permutation where all the cards appear in order: $123456.$ There are $5$ such permutations where two adjacent cards are interchanged, as in $124356.$ The other such permutations arise from removing one card from $123456$ and placing it in a position at least two away from its starting location. There are $4$ such positions to place each of the cards numbered $1$ and $6,$ and $3$ such positions for each of the cards numbered $2, 3, 4,$ and $5.$ This accounts for $2\cdot4 + 4\cdot3 =20$ permutations. Thus there are $1 + 5 + 20 = 26$ permutations where one card can be removed so that the remaining cards are in ascending order. There is an equal number of permutations that result in the cards' being in descending order. This gives the total $26 + 26 = 52$ .

Solution 6 (Official MAA 2)

More generally, suppose there are $n \geq 4$ cards numbered $1, 2, 3, \dots, n$ arranged in ascending order. If any one of the $n$ cards is removed and placed in one of the $n$ positions in the arrangement, the resulting permutation will have the property that one card can be removed so that the remaining cards are in ascending order. This accounts for $n\cdot n = n^2$ permutations. However, the original ascending order has been counted $n$ times, and each order that arises by switching two neighboring cards has been counted twice. Hence the number of arrangements where one card can be removed resulting in the remaining cards' being in ascending order is $n^2-(n-1)-(n-1)=(n-1)^2+1.$ When $n = 6$ , this is $(6-1)^2+1 = 26$ , and the final answer is $2\cdot26 = 52$ .

Solution 7 (Simple and Easy, don't know why it's hard)

For ascending you can place the $1$ in $6$ locations and the rest of the numbers in $4$ locations based on the sequence $1, 2, 3, 4, 5, 6$ . $6 + 4*5 = 26$ . Multiply by $2$ to account for the descending and get $\boxed{52}$ . ~Lopkiloinm

6.Solution 1

$[asy] size(10cm); pair A, B, C, D, O, P, H, L, X, Y; A = (-1, 0); B = (1, 0); H = (0, 0); C = (5, 0); D = (9, 0); L = (7, 0); O = (0, sqrt(160/13 - 1)); P = (7, sqrt(160/13 - 4)); X = (0, sqrt(160/13 - 4)); Y = (O + P) / 2; draw(A -- O -- B -- cycle); draw(C -- P -- D -- cycle); draw(B -- C); draw(O -- P); draw(P -- X, dashed); draw(O -- H, dashed); draw(P -- L, dashed); draw(circle(O, sqrt(160/13))); draw(circle(P, sqrt(160/13))); path b = brace(L, H); draw(b); label("$R$", O -- Y, N); label("$R$", Y -- P, N); label("$R$", O -- A, NW); label("$R$", P -- D, NE); label("$1$", A -- H, N); label("$2$", L -- D, N); label("$7$", b, S); [/asy]$

Set the common radius to $r$ . First, take the cross section of the sphere sitting in the hole of radius 1. If we draw the perpendicular bisector of the chord (the hole) through the circle, this line goes through the center. Connect the center also to where the chord hits the circle, for a right triangle with hypotenuse $r$ and base $1$ . Therefore, the height of this circle outside of the hole is $\sqrt{r^2-1}$ .

The other circle follows similarly for a height (outside the hole) of $\sqrt{r^2-4}$ . Now, if we take the cross section of the entire board, essentially making it 2-D, we can connect the centers of the two spheres, then form another right triangle with base $7$ , as given by the problem. The height of this triangle is the difference between the heights of the parts of the two spheres outside the holes, which is $\sqrt{r^2-1} - \sqrt{r^2-4}$ . Now we can set up an equation in terms of $r$ with the Pythagorean theorem: $(\sqrt{r^2-1} - \sqrt{r^2-4})^2 + 7^2 = (2r)^2.$ Simplifying a few times, $r^2 - 1 - 2\left(\sqrt{(r^2-1)(r^2-4)}\right) + r^2 - 4 + 49 = 4r^2$ $2r^2-44= -2\left(\sqrt{(r^2-1)(r^2-4)}\right)$ $22-r^2=\left(\sqrt{r^4 - 5r^2 + 4}\right)$ $r^4 -44r^2 + 484 = r^4 - 5r^2 + 4$ $39r^2=480$ $r^2=\frac{480}{39} = \frac{160}{13}.$ Therefore, our answer is $\boxed{173}$ .

-molocyxu

Solution 2 (Official MAA)

Consider a cross section of the board and spheres with a plane that passes through the centers of the holes and centers of the spheres as shown.

$[asy] unitsize(1.5 cm); pair A, B, C, D, E, F, G, P, Q; C = dir(175); D = dir(175 + 180); P = (-2,-0.8); Q = (2,-0.8); A = (C + reflect(P,Q)*(C))/2; B = (D + reflect(P,Q)*(D))/2; E = intersectionpoint(P--A, Circle(C,1)); F = intersectionpoint(B--Q, Circle(D,1)); G = (D + reflect(A,C)*(D))/2; draw(Circle(C,1)); draw(Circle(D,1)); draw(P--Q); draw(A--(C + (0,1))); draw(B--(D + (0,1))); draw(E--C--D--F); draw(D--G); dot("$A$", A, NE); dot("$B$", B, NW); dot("$C$", C, NW); dot("$D$", D, NE); dot("$E$", E, SW); dot("$F$", F, SE); dot("$G$", G, SE); [/asy]$

Let $A$ , $C$ , and $E$ be, respectively, the center of the hole with radius $1,$ the center of the sphere resting in that hole, and a point on the edge of that hole. Let $B$ , $D$ , and $F$ be the corresponding points for the hole with radius $2.$ Let $G$ be the point on $\overline{AC}$ such that $\overline{AC} \perp \overline{GD}$ . Let the radius of the spheres be $r = CE = DF$ . Because $r^2 = AE^2 + AC^2 = 1 + AC^2$ and $r^2 = BF^2 + BD^2 = 4 + BD^2$ , it follows that $CG = AC - AG = AC - BD = \sqrt{r^2 - 1} - \sqrt{r^2-4}.$ Because $DG = 7$ , $CD = 2r$ , and $CD^2 = CG^2 +GD^2$ , it follows that $4r^2 = \left(\sqrt{r^2 - 1} - \sqrt{r^2-4}\right)^{\!2} + 7^2,$ which simplifies to $r^2 = \frac{160}{13}$ . The requested sum is $160+13 = 173$ . The value of $r$ is approximately $3.5082.$

7.Solution 1

Let $k$ be the number of women selected. Then, the number of men not selected is $(11-(k-1)=12-k$ . Note that the sum of the number of women selected and the number of men not selected is constant at $12$ . Each combination of women selected and men not selected corresponds to a committee selection. Since choosing 12 individuals from the total of 23 would give $k$ women and $12-k$ men, the number of committee selections is $\binom{23}{12}$ . The answer is $\boxed{081}$ . ~awang11's sol

Solution 2 (Bash)

We casework on the amount of men on the committee.

If there are no men in the committee, there are $\dbinom{12}{1}$ ways to pick the women on the committee, for a total of $\dbinom{11}{0} \cdot \dbinom{12}{1}$ . Notice that $\dbinom{11}{0}$ is equal to $\dbinom{11}{11}$ , so the case where no men are picked can be grouped with the case where all men are picked. When all men are picked, all females must also be picked, for a total of $\dbinom{12}{12}$ . Therefore, these cases can be combined to $\dbinom{11}{0} \cdot \left(\dbinom{12}{1} + \dbinom{12}{12}\right)$ Since $\dbinom{12}{12} = \dbinom{12}{0}$ , and $\dbinom{12}{0} + \dbinom{12}{1} = \dbinom{13}{1}$ , we can further simplify this to $\dbinom{11}{0} \cdot \dbinom{13}{1}$

All other cases proceed similarly. For example, the case with one men or ten men is equal to $\dbinom{11}{1} \cdot \dbinom{13}{2}$ . Now, if we factor out a $13$ , then all cases except the first two have a factor of $121$ , so we can factor this out too to make our computation slightly easier. The first two cases (with $13$ factored out) give $1+66=67$ , and the rest gives $121(10+75+270+504) = 103,939$ . Adding the $67$ gives $104,006$ . Now, we can test for prime factors. We know there is a factor of $2$ , and the rest is $52,003$ . We can also factor out a $7$ , for $7,429$ , and the rest is $17 \cdot 19 \cdot 23$ . Adding up all the prime factors gives $2+7+13+17+19+23 = \boxed{081}$ .

Solution 3 (Vandermonde's identity)

Applying Vandermonde's identity by setting $m=12$ , $n=11$ , and $r=11$ , we obtain $\binom{23}{11}\implies$ $\boxed{081}$ . ~Lcz

Short Proof

Consider the following setup: $[asy] size(1000, 100); for(int i=0; i<23; ++i){ dot((i, 0)); } draw((10.5, -1.5)--(10.5, 1.5), dashed); [/asy]$ The dots to the left represent the men, and the dots to the right represent the women. Now, suppose we put a mark on $11$ people (the $*$ ). Those to the left of the dashed line get to be "in" on the committee if they have a mark. Those on the right side of the dashed line are already on the committee, but if they're marked they get forcibly evicted from it. If there were $x$ people marked on the left, there ends up being $12-(11-x) = x+1$ people not marked on the right. Circles represent those in the committee. $[asy] size(1000, 100); for(int i=0; i<23; ++i){ dot((i, 0)); } for(int i=0; i<23; ++i){ if(i%2==0){ if(i >= 11){ draw(circle((i, 0), 0.25)); } continue; } label("$*$", (i,0.5), N); if(i < 11){ draw(circle((i, 0), 0.25)); } } draw((10.5, -1.5)--(10.5, 1.5), dashed); [/asy]$

We have our bijection, so the number of ways will be $\binom{23}{11}$ .

~programjames1

Solution 4

Notice that the committee can consist of $k$ boys and $k+1$ girls. Summing over all possible $k$ gives $\sum_{k=0}^{11}\binom{11}{k}\binom{12}{k+1}=\binom{11}{0}\binom{12}{1}+\binom{11}{1}\binom{12}{2}+\cdots + \binom{11}{11}\binom{12}{12}$ Using the identity $\binom{n}{k}=\binom{n}{n-k}$ , and Pascal's Identity $\binom{n}{k}+\binom{n}{k+1}=\binom{n+1}{k+1}$ , we get $\sum_{k=0}^{11}\binom{11}{k}\binom{12}{k+1}=\binom{12}{12}+\binom{12}{1}\left(\binom{11}{0}+\binom{11}{1}\right)+\cdots$ $=\binom{12}{0}^2+\binom{12}{1}^2+\binom{12}{2}^2+\binom{12}{3}^2+\binom{12}{4}^2+\binom{12}{5}^2+\frac{\binom{12}{6}^2}{2}$ $=\frac{1}{2}\sum_{k=0}^{12}\binom{12}{k}^2$ Using the identity $\sum_{k=0}^n\binom{n}{k}^2=\binom{2n}{n}$ , this simplifies to $\frac{1}{2}\cdot \binom{24}{12}=\frac{24\cdot 23\cdot 22\cdot 21\cdot 20\cdot 19\cdot 18\cdot 17\cdot 16\cdot 15\cdot 14\cdot 13}{2\cdot 12\cdot 11\cdot 10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2}=2\cdot 7\cdot 13\cdot 17\cdot 19\cdot 23$ so the desired answer is $2+7+13+17+19+23=\boxed{081}$ ~ktong

Solution 5 (Official MAA)

Select any $11$ club members. That group will have $i$ men and $11-i$ women, so the number of women in the club not selected in that group is $12 - (11-i) = i+1$ . Thus, if the committee includes the men who were selected and the women who were not selected, the committee would have the correct number of men and women. Conversely, for every committee that could be formed with $i$ men and $i+1$ women, the men on this committee together with the women not on the committee comprise a subset of $i + (12 - (i+1)) = 11$ club members. Thus $N = \binom{23}{11}= \frac{23\cdot22\cdot21\cdot20\cdot19\cdot18\cdot17\cdot16\cdot15\cdot14\cdot13}{11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}=23\cdot19\cdot17\cdot13\cdot7\cdot2.$ The requested sum is $23+19+17+13+7+2=81.$

8.Solution 1 (Coordinates)

$[asy] size(8cm); pair O, A, B, C, D, F, G, P, X; O = (0, 0); A = (5, 0); X = (8, 0); P = (5, 5 / sqrt(3)); B = rotate(-120, A) * ((O + A) / 2); C = rotate(-120, B) * ((A + B) / 2); D = rotate(-120, C) * ((B + C) / 2); F = rotate(-120, D) * ((C + D) / 2); G = rotate(-120, F) * ((D + F) / 2); draw(O -- A -- B -- C -- D -- F -- G); draw(A -- X, dashed); markscalefactor = 0.05; path angle = anglemark(X, A, B); draw(angle); dot(P); dot(O); label("$O$", O, W); label("$P$", P, E); label("$60^\circ$", angle, ENE*3); [/asy]$

We plot this on the coordinate grid with point $O$ as the origin. We will keep a tally of the x-coordinate and y-coordinate separately.

First move: The ant moves right $5$ . Second move: We use properties of a $30-60-90$ triangle to get $\frac{5}{4}$ right, $\frac{5\sqrt{3}}{4}$ up. Third move: $\frac{5}{8}$ left, $\frac{5\sqrt{3}}{8}$ up. Fourth move: $\frac{5}{8}$ left. Fifth move: $\frac{5}{32}$ left, $\frac{5\sqrt{3}}{32}$ down. Sixth move: $\frac{5}{64}$ right, $\frac{5\sqrt{3}}{64}$ down.

Total of x-coordinate: $5 + \frac{5}{4} - \frac{5}{8} - \frac{5}{8} - \frac{5}{32} + \frac{5}{64} = \frac{315}{64}$ . Total of y-coordinate: $0 + \frac{5\sqrt{3}}{4} + \frac{5\sqrt{3}}{8} + 0 - \frac{5\sqrt{3}}{32} - \frac{5\sqrt{3}}{64} = \frac{105\sqrt{3}}{64}$ .

After this cycle of six moves, all moves repeat with a factor of $(\frac{1}{2})^6 = \frac{1}{64}$ . Using the formula for a geometric series, multiplying each sequence by $\frac{1}{1-\frac{1}{64}} = \frac{64}{63}$ will give us the point $P$ .

$\frac{315}{64} \cdot \frac{64}{63} = 5$ , $\frac{105\sqrt{3}}{64} \cdot \frac{64}{63} = \frac{5\sqrt{3}}{3}$ . Therefore, the coordinates of point $P$ are $(5,\frac{5\sqrt{3}}{3})$ , so using the Pythagorean Theorem, $OP^2 = \frac{100}{3}$ , for an answer of $\boxed{103}$ .

-molocyxu

Solution 2 (Complex)

We place the ant at the origin of the complex plane with its first move being in the positive real direction. Then the ant's journey can be represented as the infinite series $5\left(1 + \frac{e^{\frac{i\pi}{3}}}{2} + \left(\frac{e^{\frac{i\pi}{3}}}{2}\right)^2 + \cdots\right)$ Using the formula for an infinite geometric series, this is equal to $\frac{5}{1 - \frac12e^{\frac{i\pi}{3}}} = \frac{5}{1 - \frac{1 + i\sqrt{3}}{4}} = \frac{20}{3 - i\sqrt{3}} = 5 + \frac{5i\sqrt{3}}{3}$ We are looking for the square of the modulus of this value: $\left|\frac{5 + 5i\sqrt{3}}{3}\right|^2 = 25 + \frac{25}{3} = \frac{100}{3}$ so the answer is $100 + 3 = \boxed{103}$ .

Solution 3 (Solution 1 faster)

The ant goes in the opposite direction every $3$ moves, going $(1/2)^3=1/8$ the distance backwards. Using geometric series, he travels $1-1/8+1/64-1/512...=(7/8)(1+1/64+1/4096...)=(7/8)(64/63)=8/9$ the distance of the first three moves over infinity moves. Now, we use coordinates meaning $(5+5/4-5/8, 0+5\sqrt3/4+5\sqrt3/8)$ or $(45/8, 15\sqrt3/8)$ . Multiplying these by $8/9$ , we get $(5, 5\sqrt3/3)$ $\implies$ $\boxed{103}$ .

~Lcz

Solution 4 (Official MAA 1)

Suppose that the bug starts at the origin $(0,0)$ and travels a distance of $a$ units due east on the first day, and that there is a real number $r$ with $0<r < 1$ such that each day after the first, the bug walks $r$ times as far as the previous day. On day $n$ , the bug travels along the vector $\pmb v_{n}$ that has magnitude $ar^{n-1}$ and direction $\langle\cos(n\cdot 60^\circ),\sin(n\cdot 60^\circ)\rangle$ . Then $P$ is the terminal point of the infinite sum of the vectors $\pmb v_{1}+\pmb v_{2}+\pmb v_3+\cdots$ . The $x$ -coordinate of this sum is $a\big(\!\cos0^\circ+r\cos60^\circ + r^{2}\cos120^\circ+r^{3}\cos180^\circ+r^{4}\cos240^\circ$ $+r^{5}\cos300^\circ+r^{6}\cos360^\circ+\cdots\big).$ Because the angles repeat after 6 terms, this sum is equal to $aS(1+r^{6}+r^{12}+r^{18}+\cdots)=\frac{aS}{1-r^{6}},$ where $S=\cos0^\circ+r\cos60^\circ + r^{2}\cos120^\circ+r^{3}\cos180^\circ+r^{4}\cos240^\circ+ r^{5}\cos300^\circ.$ Similarly, the $y$ -coordinate of $P$ will be $\displaystyle{\frac{aT}{1-r^{6}}}$ , where $T=\sin0^\circ+r\sin60^\circ + r^{2}\sin120^\circ+r^{3}\sin180^\circ+r^{4}\sin240^\circ+ r^{5}\sin300^\circ.$ In this case $r=\frac12$ and $a = 5$ , so $S=1+\frac14-\frac18-\frac18-\frac1{32}+\frac1{64}=\frac{63}{64},$ $T=0+\frac{\sqrt3}4+\frac{\sqrt3}8+0-\frac{\sqrt3}{32}-\frac{\sqrt3}{64}=\frac{21\sqrt3}{64},$ and the coordinates of $P$ are $\left(\frac{5S}{1-\frac1{64}}, \frac{5T}{1-\frac1{64}}\right)=\left(5,\frac{5\sqrt3}{3}\right).$ Thus the square of the distance from the origin to $P$ is $25+\frac{25}3=\frac{100}3$ . The requested sum is $100+3=103$ .

Solution 5 (Official MAA 2)

Let point $O$ be the origin in the complex plane. Point $P$ is the complex sum $5(1+z+z^2+\cdots) = \frac{5}{1-z}$ , where $z=\frac{1+i\sqrt3}4$ . The distance squared is ${OP}^2=\left|\frac5{1-\frac{1+i\sqrt3}4}\right|^{2}= \frac{(4\cdot5)^2}{\left|4-(1+i\sqrt3)\right|^2}=\frac{400}{9+3}=\frac{100}3.$

9.Solution 1

$[asy] size(12cm); for (int x = 1; x < 18; ++x) { draw((x, 0) -- (x, 9), dotted); } for (int y = 1; y < 9; ++y) { draw((0, y) -- (18, y), dotted); } draw((0, 0) -- (18, 0) -- (18, 9) -- (0, 9) -- cycle); pair b1, b2, b3; pair c1, c2, c3; pair a1, a2, a3; b1 = (3, 0); b2 = (12, 0); b3 = (16, 0); c1 = (0, 2); c2 = (0, 4); c3 = (0, 8); a1 = b1 + c1; a2 = b2 + c2; a3 = b3 + c3; draw(b1 -- a1 -- c1); draw(b2 -- a2 -- c2); draw(b3 -- a3 -- c3); dot(a1); dot(a2); dot(a3); label("$a_1$", a1, NE); label("$a_2$", a2, NE); label("$a_3$", a3, NE); label("$b_1$", b1, S); label("$b_2$", b2, S); label("$b_3$", b3, S); label("$c_1$", c1, W); label("$c_2$", c2, W); label("$c_3$", c3, W); [/asy]$

First, prime factorize $20^9$ as $2^{18} \cdot 5^9$ . Denote $a_1$ as $2^{b_1} \cdot 5^{c_1}$ , $a_2$ as $2^{b_2} \cdot 5^{c_2}$ , and $a_3$ as $2^{b_3} \cdot 5^{c_3}$ .

In order for $a_1$ to divide $a_2$ , and for $a_2$ to divide $a_3$ , $b_1\le b_2\le b_3$ , and $c_1\le c_2\le c_3$ . We will consider each case separately. Note that the total amount of possibilities is $190^3$ , as there are $(18+1)(9+1)=190$ choices for each factor.

We notice that if we add $1$ to $b_2$ and $2$ to $b_3$ , then we can reach the stronger inequality $0\le b_1<b_2+1<b_3+2\le 20$ . Therefore, if we pick $3$ integers from $0$ to $20$ , they will correspond to a unique solution, forming a 1-1 correspondence between the numbers $b_1$ , $b_2+1$ , and $b_3+2$ . This is also equivalent to applying stars and bars on distributing the powers of 2 and 5 through differences. The amount of solutions to this inequality is $\dbinom{21}{3}$ .

The case for $c_1$ , $c_2$ , and $c_3$ proceeds similarly for a result of $\dbinom{12}{3}$ . Therefore, the probability of choosing three such factors is $\frac{\dbinom{21}{3} \cdot \dbinom{12}{3}}{190^3}.$ Simplification gives $\frac{77}{1805}$ , and therefore the answer is $\boxed{077}$ .

-molocyxu

Solution 2

Same as before, say the factors have powers of $b$ and $c$ . $b_1, b_2, b_3$ can either be all distinct, all equal, or two of the three are equal. As well, we must have $b_1 \leq b_2 \leq b_3$ . If they are all distinct, the number of cases is simply ${19 \choose 3}$ . If they are all equal, there are only $19$ cases for the general value. If we have a pair equal, then we have $2 \cdot {19\choose 2}$ . We need to multiply by $2$ because if we have two values $b_i < b_j$ , we can have either $(b_i, b_i, b_j)$ or $(b_i, b_j, b_j)$ .

${19 \choose 3} + 2 \cdot {19 \choose 2} + 19 = 1330$

Likewise for $c$ , we get

${10 \choose 3} + 2 \cdot {10 \choose 2} + 10 = 220$

The final probability is simply $\frac{1330 \cdot 220}{190^3}$ . Simplification gives $\frac{77}{1805}$ , and therefore the answer is $\boxed{077}$ .

Solution 3

Similar to before, we calculate that there are $190^3$ ways to choose $3$ factors with replacement. Then, we figure out the number of triplets ${a,b,c}$ and ${d,f,g}$ , where $a$ , $b$ , and $c$ represent powers of $2$ and $d$ , $f$ , and $g$ represent powers of $5$ , such that the triplets are in non-descending order. The maximum power of $2$ is $18$ , and the maximum power of $5$ is $9$ . Using the Hockey Stick identity, we figure out that there are $\dbinom{12}{3}$ ways to choose $d$ , $f$ and $g$ , and $\dbinom{21}{3}$ ways to choose $a$ , $b$ , and $c$ . Therefore, the probability of choosing $3$ factors which satisfy the conditions is $\frac{\dbinom{21}{3} \cdot \dbinom{12}{3}}{190^3}.$ This simplifies to $\frac{77}{1805}$ , therefore $m =$ $\boxed{077}$ .

10.Solution 1

Taking inspiration from $4^4 \mid 10^{10}$ we are inspired to take $n$ to be $p^2$ , the lowest prime not dividing $210$ , or $11 \implies n = 121$ . Now, there are $242$ factors of $11$ , so $11^{242} \mid m^m$ , and then $m = 11k$ for $k \geq 22$ . Now, $\gcd(m+n, 210) = \gcd(11+k,210) = 1$ . Noting $k = 26$ is the minimal that satisfies this, we get $(n,m) = (121,286)$ . Thus, it is easy to verify this is minimal and we get $\boxed{407}$ . ~awang11

Solution 2

Assume for the sake of contradiction that $n$ is a multiple of a single digit prime number, then $m$ must also be a multiple of that single digit prime number to accommodate for $n^n | m^m$ . However that means that $m+n$ is divisible by that single digit prime number, which violates $\gcd(m+n,210) = 1$ , so contradiction.

$n$ is also not 1 because then $m$ would be a multiple of it.

Thus, $n$ is a multiple of 11 and/or 13 and/or 17 and/or...

Assume for the sake of contradiction that $n$ has at most 1 power of 11, at most 1 power of 13...and so on... Then, for $n^n | m^m$ to be satisfied, $m$ must contain at least the same prime factors that $n$ has. This tells us that for the primes where $n$ has one power of, $m$ also has at least one power, and since this holds true for all the primes of $n$ , $n|m$ . Contradiction.

Thus $n$ needs more than one power of some prime. The obvious smallest possible value of $n$ now is $11^2 =121$ . Since $121^{121}=11^{242}$ , we need $m$ to be a multiple of 11 at least $242$ that is not divisible by $121$ and most importantly, $\gcd(m+n,210) = 1$ . $242$ is divisible by $121$ , out. $253+121$ is divisible by 2, out. $264+121$ is divisible by 5, out. $275+121$ is divisible by 2, out. $286+121=37\cdot 11$ and satisfies all the conditions in the given problem, and the next case $n=169$ will give us at least $169\cdot 3$ , so we get $\boxed{407}$ .

11.Solution 1 (Strategic Casework)

Either $f(2)=f(4)$ or not. If it is, note that Vieta's forces $a = -6$ . Then, $b$ can be anything. However, $c$ can also be anything, as we can set the root of $g$ (not equal to $f(2) = f(4)$ ) to any integer, producing a possible integer value of $d$ . Therefore there are $21^2 = 441$ in this case*. If it isn't, then $f(2),f(4)$ are the roots of $g$ . This means by Vieta's, that:

$f(2)+f(4) = -c \in [-10,10]$ $20 + 6a + 2b \in [-10,10]$ $3a + b \in [-15,-5].$

Solving these inequalities while considering that $a \neq -6$ to prevent $f(2) = f(4)$ , we obtain $69$ possible tuples and adding gives $441+69=\boxed{510}$ . ~awang11

Solution 2 (Bash)

Define $h(x)=x^2+cx$ . Since $g(f(2))=g(f(4))=0$ , we know $h(f(2))=h(f(4))=-d$ . Plugging in $f(x)$ into $h(x)$ , we get $h(f(x))=x^4+2ax^3+(2b+a^2+c)x^2+(2ab+ac)x+(b^2+bc)$ . Setting $h(f(2))=h(f(4))$ , $16+16a+8b+4a^2+4ab+b^2+4c+2ac+bc=256+128a+32b+16a^2+8ab+b^2+16c+4ac+bc$ . Simplifying and cancelling terms, $240+112a+24b+12a^2+4ab+12c+2ac=0$ $120+56a+12b+6a^2+2ab+6c+ac=0$ $6a^2+2ab+ac+56a+12b+6c+120=0$ $6a^2+2ab+ac+20a+36a+12b+6c+120=0$ $a(6a+2b+c+20)+6(6a+2b+c+20)=0$ $(a+6)(6a+2b+c+20)=0$

Therefore, either $a+6=0$ or $6a+2b+c=-20$ . The first case is easy: $a=-6$ and there are $441$ tuples in that case. In the second case, we simply perform casework on even values of $c$ , to get $77$ tuples, subtracting the $8$ tuples in both cases we get $441+77-8=\boxed{510}$ .

-EZmath2006

Notes For *

In case anyone is confused by this (as I initially was). In the case where $f(2)=f(4)$ , this does not mean that g has a double root of $f(2)=f(4)=k$ , ONLY that $k$ is one of the roots of g. So basically since $a=-6$ in this case, $f(2)=f(4)=b-8$ , and we have $21$ choices for b and we still can ensure c is an integer with absolute value less than or equal to 10 simply by having another integer root of g that when added to $b-8$ ensures this, and of course an integer multiplied by an integer is an integer so $d$ will still be an integer. In other words, you have can have $b$ and $c$ be any integer with absolute value less than or equal to 10 with $d$ still being an integer. Now refer back to the 1st solution. ~First

12.Solution 1

Lifting the Exponent shows that $v_3(149^n-2^n) = v_3(n) + v_3(147) = v_3(n)+1$ so thus, $3^2$ divides $n$ . It also shows that $v_7(149^n-2^n) = v_7(n) + v_7(147) = v_7(n)+2$ so thus, $7^5$ divides $n$ .

Now, multiplying $n$ by $4$ , we see $v_5(149^{4n}-2^{4n}) = v_5(149^{4n}-16^{n})$ and since $149^{4} \equiv 1 \pmod{25}$ and $16^1 \equiv 16 \pmod{25}$ then $v_5(149^{4n}-2^{4n})=1+v_5(n)$ meaning that we have that by LTE, $4 \cdot 5^4$ divides $n$ .

Since $3^2$ , $7^5$ and $4\cdot 5^4$ all divide $n$ , the smallest value of $n$ working is their LCM, also $3^2 \cdot 7^5 \cdot 4 \cdot 5^4 = 2^2 \cdot 3^2 \cdot 5^4 \cdot 7^5$ . Thus the number of divisors is $(2+1)(2+1)(4+1)(5+1) = \boxed{270}$ .

~kevinmathz

Solution 2 (Simpler, just basic mods and Fermat's theorem)

Note that for all $n$ , $149^n - 2^n$ is divisible by $149-2 = 147$ because that is a factor. That is $3\cdot7^2$ , so now we can clearly see that the smallest $n$ to make the expression divisible by $3^3$ is just $3^2$ . Similarly, we can reason that the smallest $n$ to make the expression divisible by $7^7$ is just $7^5$ .

Finally, for $5^5$ , take $\pmod {5}$ and $\pmod {25}$ of each quantity (They happen to both be $-1$ and $2$ respectively, so you only need to compute once). One knows from Fermat's theorem that the maximum possible minimum $n$ for divisibility by $5$ is $4$ , and other values are factors of $4$ . Testing all of them(just $1$ , $2$ , $4$ using mods-not too bad), $4$ is indeed the smallest value to make the expression divisible by $5$ , and this clearly is NOT divisible by $25$ . Therefore, the smallest $n$ to make this expression divisible by $5^5$ is $2^2 \cdot 5^4$ .

Calculating the LCM of all these, one gets $2^2 \cdot 3^2 \cdot 5^4 \cdot 7^5$ . Using the factor counting formula, the answer is $3\cdot3\cdot5\cdot6$ = $\boxed{270}$ .

~Solution by thanosaops

~formatted by MY-2

~also formatted by pandyhu2001

Solution 3 (Elementary and Thorough)

As usual, denote $v_p(n)$ the highest power of prime $p$ that divides $n$ . For divisibility by $3^3$ , notice that $v_3(149^3 - 2^3) = 2$ as $149^3 - 2^3 =$ $(147)(149^2 + 2\cdot149 + 2^2)$ , and upon checking mods, $149^2 + 2\cdot149 + 2^2$ is divisible by $3$ but not $9$ . In addition, $149^9 - 2^9$ is divisible by $3^3$ because $149^9 - 2^9 = (149^3 - 2^3)(149^6 + 149^3\cdot2^3 + 2^6)$ , and the rightmost factor equates to $1 + 1 + 1 \pmod{3} \equiv 0 \pmod{3}$ . In fact, $n = 9 = 3^2$ is the least possible choice to ensure divisibility by $3^3$ because if $n = a \cdot 3^b$ , with $3 \nmid a$ and $b < 2$ , we write $149^{a \cdot 3^b} - 2^{a \cdot 3^b} = (149^{3^b} - 2^{3^b})(149^{3^b(a - 1)} + 149^{3^b(a - 2)}\cdot2^{3^b}+\cdots2^{3^b(a - 1)}).$ Then, the rightmost factor is equivalent to $\pm a \pmod{3} \not\equiv 0 \pmod{3}$ , and $v_3(149^{3^b} - 2^{3^b}) = b + 1 < 3$ .

For divisibility by $7^7$ , we'll induct, claiming that $v_7(149^{7^k} - 2^{7^k}) = k + 2$ for whole numbers $k$ . The base case is clear. Then, $v_7(149^{7^{k+1}} - 2^{7^{k+1}}) = v_7(149^{7^k} - 2^{7^k}) + v_7(149^{6\cdot7^k} + 2^{7^k}\cdot149^{5\cdot7^k} + \cdots + 2^{5\cdot7^k}\cdot149^{7^k} + 2^{6\cdot7^k}).$ By the induction hypothesis, $v_7(149^{7^k} - 2^{7^k}) = k + 2$ . Then, notice that $S(k) = 149^{6\cdot7^k} + 2^{7^k}\cdot149^{5\cdot7^k} + \cdots + 2^{5\cdot7^k}\cdot149^{7^k} + 2^{6\cdot7^k} \equiv 7 \cdot 2^{6\cdot7^k}\pmod{7} \equiv 7 \cdot 2^{6\cdot7^k}\pmod{49}.$ This tells us that $S(k)$ is divisible by $7$ , but not $49$ so that $v_7\left(S(k)\right) = 1$ , completing our induction. We can verify that $7^5$ is the least choice of $n$ to ensure divisibility by $7^7$ by arguing similarly to the $3^3$ case.

Finally, for $5^5$ , we take the powers of $149$ and $2$ in mod $5$ and mod $25$ . Writing out these mods, we have that $149^n \equiv 2^n \pmod{5}$ if and only if $4 | n$ , in which $149^n \equiv 2^n \equiv 1 \pmod{5}$ . So here we claim that $v_5(149^{4\cdot5^k} - 2^{4\cdot5^k}) = k + 1$ and perform yet another induction. The base case is true: $5 | 149^4 - 2^4$ , but $149^4 - 2^4 \equiv 1 - 16 \pmod{25}$ . Now then, assuming the induction statement to hold for some $k$ , $v_5(149^{4\cdot5^{k+1}} - 2^{4\cdot5^{k+1}}) = (k+1) + v_5(149^{4\cdot4\cdot5^k}+2^{4\cdot5^k}\cdot149^{3\cdot4\cdot5^k}+\cdots+2^{3\cdot4\cdot5^k}\cdot149^{4\cdot5^k}+2^{4\cdot4\cdot5^k}).$ Note that $S'(k) = 149^{4\cdot4\cdot5^k}+2^{4\cdot5^k}\cdot149^{3\cdot4\cdot5^k}+\cdots+2^{3\cdot4\cdot5^k}\cdot149^{4\cdot5^k}+2^{4\cdot4\cdot5^k}$ equates to $S''(k) = 1 + 2^{4\cdot5^k} + \cdots + 2^{16\cdot5^k}$ in both mod $5$ and mod $25$ . We notice that $S''(k) \equiv 0 \pmod{5}$ . Writing out the powers of $2$ mod $25$ , we have $S''(0) \equiv 5 \pmod{25}$ . Also $2^n \equiv 1 \pmod{25}$ when $n$ is a multiple of $20$ . Hence for $k > 0$ , $S''(k) \equiv 5 \mod{25}$ . Thus, $v_5\left(S'(k)\right) = 1$ , completing our induction. Applying the same argument from the previous two cases, $4\cdot5^4$ is the least choice to ensure divisibility by $5^5$ .

Our answer is the number of divisors of $\text{lcm}(3^2, 7^5, 2^2\cdot5^4) = 2^2 \cdot 3^2 \cdot 5^4 \cdot 7^5$ . It is $(2 + 1)(2 + 1)(4 + 1)(5 + 1) = \boxed{270}$ .

~hnkevin42

13.Solution 1

Points are defined as shown. It is pretty easy to show that $\triangle AFE \sim \triangle AGH$ by spiral similarity at $A$ by some short angle chasing. Now, note that $AD$ is the altitude of $\triangle AFE$ , as the altitude of $AGH$ . We need to compare these altitudes in order to compare their areas. Note that Stewart's theorem implies that $AD/2 = \frac{\sqrt{18}}{2}$ , the altitude of $\triangle AFE$ . Similarly, the altitude of $\triangle AGH$ is the altitude of $\triangle ABC$ , or $\frac{12}{\sqrt{7}}$ . However, it's not too hard to see that $GB = HC = 1$ , and therefore $[AGH] = [ABC]$ . From here, we get that the area of $\triangle ABC$ is $\frac{15\sqrt{7}}{14} \implies \boxed{036}$ , by similarity. ~awang11

Solution 2(coord bash + basic geometry)

Let $\overline{BC}$ lie on the x-axis and $B$ be the origin. $C$ is $(5,0)$ . Use Heron's formula to compute the area of triangle $ABC$ . We have $s=\frac{15}{2}$ . and $[ABC]=\sqrt{\frac{15 \cdot 7 \cdot 5 \cdot 3}{2^4}}=\frac{15\sqrt{7}}{4}$ . We now find the altitude, which is $\frac{\frac{15\sqrt{7}}{2}}{5}=\frac{3\sqrt{7}}{2}$ , which is the y-coordinate of $A$ . We now find the x-coordinate of $A$ , which satisfies $x^2 + (\frac{3\sqrt{7}}{2})^{2}=16$ , which gives $x=\frac{1}{2}$ since the triangle is acute. Now using the Angle Bisector Theorem, we have $\frac{4}{6}=\frac{BD}{CD}$ and $BD+CD=5$ to get $BD=2$ . The coordinates of D are $(2,0)$ . Since we want the area of triangle $AEF$ , we will find equations for perpendicular bisector of AD, and the other two angle bisectors. The perpendicular bisector is not too challenging: the midpoint of AD is $(\frac{5}{4}, \frac{3\sqrt{7}}{4})$ and the slope of AD is $-\sqrt{7}$ . The slope of the perpendicular bisector is $\frac{1}{\sqrt{7}}$ . The equation is(in point slope form) $y-\frac{3\sqrt{7}}{4}=\frac{1}{\sqrt{7}}(x-\frac{5}{4})$ . The slope of AB, or in trig words, the tangent of $\angle ABC$ is $3\sqrt{7}$ . Finding $\sin{\angle ABC}=\frac{\frac{3\sqrt{7}}{2}}{4}=\frac{3\sqrt{7}}{8}$ and $\cos{\angle ABC}=\frac{\frac{1}{2}}{4}=\frac{1}{8}$ . Plugging this in to half angle tangent, it gives $\frac{\frac{3\sqrt{7}}{8}}{1+\frac{1}{8}}=\frac{\sqrt{7}}{3}$ as the slope of the angle bisector, since it passes through $B$ , the equation is $y=\frac{\sqrt{7}}{3}x$ . Similarly, the equation for the angle bisector of $C$ will be $y=-\frac{1}{\sqrt{7}}(x-5)$ . For $E$ use the B-angle bisector and the perpendicular bisector of AD equations to intersect at $(3,\sqrt{7})$ . For $F$ use the C-angle bisector and the perpendicular bisector of AD equations to intersect at $(\frac{1}{2}, \frac{9}{2\sqrt{7}})$ . The area of AEF is equal to $\frac{EF \cdot \frac{AD}{2}}{2}$ since AD is the altitude of that triangle with EF as the base, with $\frac{AD}{2}$ being the height. $EF=\frac{5\sqrt{2}}{\sqrt{7}}$ and $AD=3\sqrt{2}$ , so $[AEF]=\frac{15}{2\sqrt{7}}=\frac{15\sqrt{7}}{14}$ which gives $\boxed{036}$ . NEVER overlook coordinate bash in combination with beginner synthetic techniques.~vvluo

Solution 3 (Coordinate Bash + Trig)

$[asy] size(8cm); defaultpen(fontsize(10pt)); pair A,B,C,I,D,M,T,Y,Z,EE,F; A=(0,3sqrt(7)); B=(-1,0); C=(9,0); I=incenter(A,B,C); D=extension(A,I,B,C); M=(A+D)/2; draw(B--EE,gray+dashed); draw(C--F,gray+dashed); draw(A--B--C--A); draw(A--D); draw(B--(5,sqrt(28))); draw(M--(5,sqrt(28))); draw(C--(0,9sqrt(7)/7)); draw(M--(0,9sqrt(7)/7)); dot("$A$",A,NW); dot("$B$",B,SW); dot("$C$",C,SE); dot("$D$",D,S); dot("$E$",(5,sqrt(28)),N); dot("$M$",M,dir(70)); dot("$F$",(0,9sqrt(7)/7),N); label("$2$",B--D,S); label("$3$",D--C,S); label("$6$",A--C,N); label("$4$",A--B,W); [/asy]$

Let $B=(0,0)$ and $BC$ be the line $y=0$ . We compute that $\cos{\angle{ABC}}=\frac{1}{8}$ , so $\tan{\angle{ABC}}=3\sqrt{7}$ . Thus, $A$ lies on the line $y=3x\sqrt{7}$ . The length of $AB$ at a point $x$ is $8x$ , so $x=\frac{1}{2}$ .

We now have the coordinates $A=\left(\frac{1}{2},\frac{3\sqrt{7}}{2}\right)$ , $B=(0,0)$ and $C=(5,0)$ . We also have $D=(2,0)$ by the angle-bisector theorem and $M=\left(\frac{5}{4},\frac{3\sqrt{7}}{4}\right)$ by taking the midpoint. We have that because $\cos{\angle{ABC}}=\frac{1}{8}$ , $\cos{\frac{\angle{ABC}}{2}}=\frac{3}{4}$ by half angle formula.

We also compute $\cos{\angle{ACB}}=\frac{3}{4}$ , so $\cos{\frac{\angle{ACB}}{2}}=\frac{\sqrt{14}}{4}$ .

Now, $AD$ has slope $-\frac{\frac{3\sqrt{7}}{2}}{2-\frac{1}{2}}=-\sqrt{7}$ , so it's perpendicular bisector has slope $\frac{\sqrt{7}}{7}$ and goes through $\left(\frac{5}{4},\frac{3\sqrt{7}}{4}\right)$ .

We find that this line has equation $y=\frac{\sqrt{7}}{7}x+\frac{4\sqrt{7}}{7}$ .

As $\cos{\angle{CBI}}=\frac{3}{4}$ , we have that line $BI$ has form $y=\frac{\sqrt{7}}{3}x$ . Solving for the intersection point of these two lines, we get $x=3$ and thus $E=\left(3, \sqrt{7}\right)$

We also have that because $\cos{\angle{ICB}}=\frac{\sqrt{14}}{4}$ , $CI$ has form $y=-\frac{x\sqrt{7}}{7}+\frac{5\sqrt{7}}{7}$ .

Intersecting the line $CI$ and the perpendicular bisector of $AD$ yields $-\frac{x\sqrt{7}}{7}+\frac{5\sqrt{7}}{7}=\frac{x\sqrt{7}}{7}+\frac{4\sqrt{7}}{7}$ .

Solving this, we get $x=\frac{1}{2}$ and so $F=\left(\frac{1}{2},\frac{9\sqrt{7}}{14}\right)$ .

We now compute $EF=\sqrt{\left(\frac{5}{2}\right)^2+\left(\frac{5\sqrt{7}}{14}\right)^2}=\frac{5\sqrt{14}}{7}$ . We also have $MA=\sqrt{\left(\frac{3}{4}\right)^2+\left(\frac{3\sqrt{7}}{4}\right)^2}=\frac{3\sqrt{2}}{2}$ .

As ${MA}\perp{EF}$ , we have $[\triangle{AEF}]=\frac{1}{2}\left(\frac{3\sqrt{2}}{2}\times\frac{5\sqrt{14}}{7}\right)=\frac{15\sqrt{7}}{14}$ .

The desired answer is $15+7+14=\boxed{036}$ ~Imayormaynotknowcalculus

Solution 4 (Barycentric Coordinates)

As usual, we will use homogenized barycentric coordinates.

We have that $AD$ will have form $3z=2y$ . Similarly, $CF$ has form $5y=6x$ and $BE$ has form $5z=4x$ . Since $A=(1,0,0)$ and $D=\left(0,\frac{3}{5},\frac{2}{5}\right)$ , we also have $M=\left(\frac{1}{2},\frac{3}{10},\frac{1}{5}\right)$ . It remains to determine the equation of the line formed by the perpendicular bisector of $AD$ .

This can be found using EFFT. Let a point $T$ on $EF$ have coordinates $(x, y, z)$ . We then have that the displacement vector $\overrightarrow{AD}=\left(-1, \frac{3}{5}, \frac{2}{5}\right)$ and that the displacement vector $\overrightarrow{TM}$ has form $\left(x-\frac{1}{2},y-\frac{3}{10},z-\frac{1}{5}\right)$ . Now, by EFFT, we have $5^2\left(\frac{3}{5}\times\left(z-\frac{1}{5}\right)+\frac{2}{5}\times\left(y-\frac{3}{10}\right)\right)+6^2\left(-1\times\left(z-\frac{1}{5}\right)+\frac{2}{5}\times\left(x-\frac{1}{2}\right)\right)+4^2\left(-1\times\left(y-\frac{3}{10}\right)+\frac{3}{5}\times\left(x-\frac{1}{2}\right)\right)=0$ . This equates to $8x-2y-7z=2$ .

Now, intersecting this with $BE$ , we have $5z=4x$ , $8x-2y-7z=2$ , and $x+y+z=1$ . This yields $x=\frac{2}{3}$ , $y=-\frac{1}{5}$ , and $z=\frac{8}{15}$ , or $E=\left(\frac{2}{3},-\frac{1}{5},\frac{8}{15}\right)$ .

Similarly, intersecting this with $CF$ , we have $5y=6x$ , $8x-2y-7z=2$ , and $x+y+z=1$ . Solving this, we obtain $x=\frac{3}{7}$ , $y=\frac{18}{35}$ , and $z=\frac{2}{35}$ , or $F=\left(\frac{3}{7},\frac{18}{35},\frac{2}{35}\right)$ .

We finish by invoking the Barycentric Distance Formula twice; our first displacement vector being $\overrightarrow{FE}=\left(\frac{5}{21},-\frac{5}{7},\frac{10}{21}\right)$ . We then have $FE^2=-25\left(-\frac{5}{7}\cdot\frac{10}{21}\right)-36\left(\frac{5}{21}\cdot\frac{10}{21}\right)-16\left(\frac{5}{21}\cdot-\frac{5}{7}\right)=\frac{50}{7}$ , thus $FE=\frac{5\sqrt{14}}{7}$ .

Our second displacement vector is $\overrightarrow{AM}=\left(-\frac{1}{2},\frac{3}{10},\frac{1}{5}\right)$ . As a result, $AM^2=-25\left(\frac{3}{10}\cdot\frac{1}{5}\right)-36\left(-\frac{1}{2}\cdot\frac{1}{5}\right)-16\left(-\frac{1}{2}\cdot\frac{3}{10}\right)=\frac{9}{2}$ , so $AM=\frac{3\sqrt{2}}{2}$ .

As ${AM}\perp{EF}$ , the desired area is $\frac{\frac{5\sqrt{14}}{7}\times\frac{3\sqrt{2}}{2}}{2}={\frac{15\sqrt{7}}{14}}\implies{m+n+p=\boxed{036}}$ . ~Imayormaynotknowcalculus

Remark: The area of $\triangle{AEF}$ can also be computed using the Barycentric Area Formula, although it may increase the risk of computational errors; there are also many different ways to proceed once the coordinates are determined.

Solution 5 (geometry+trig)

$[asy] size(8cm); defaultpen(fontsize(10pt)); pair A,B,C,I,D,M,T,Y,Z,EE,F; A=(0,3sqrt(7)); B=(-1,0); C=(9,0); I=incenter(A,B,C); D=extension(A,I,B,C); M=(A+D)/2; draw(B--EE,gray+dashed); draw(C--F,gray+dashed); draw(A--B--C--A); draw(A--D); draw(A--(5,sqrt(28))); draw(A--(0,9sqrt(7)/7)); draw(D--(0,9sqrt(7)/7)); draw(D--(5,sqrt(28))); draw(B--(5,sqrt(28))); draw(M--(5,sqrt(28))); draw(C--(0,9sqrt(7)/7)); draw(M--(0,9sqrt(7)/7)); dot("$A$",A,NW); dot("$B$",B,SW); dot("$C$",C,SE); dot("$D$",D,S); dot("$E$",(5,sqrt(28)),N); dot("$M$",M,dir(70)); dot("$F$",(0,9sqrt(7)/7),N); label("$2$",B--D,S); label("$3$",D--C,S); label("$6$",A--C,N); label("$4$",A--B,W); [/asy]$

To get the area of $\triangle AEF$ , we try to find $AM$ and $\angle EAF$ .

Since $AD$ is the angle bisector, we can get that $BD=2$ and $CD=3$ . By applying Stewart's Theorem, we can get that $AD=3\sqrt{2}$ . Therefore $AM=\frac{3\sqrt{2}}{2}$ .

Since $EF$ is the perpendicular bisector of $AD$ , we know that $AE = DE$ . Since $BE$ is the angle bisector of $\angle BAC$ , we know that $\angle ABE = \angle DBE$ . By applying the Law of Sines to $\triangle ABE$ and $\triangle DBE$ , we know that $\sin \angle BAE = \sin \angle BDE$ . Since $BD$ is not equal to $AB$ and therefore these two triangles are not congruent, we know that $\angle BAE$ and $\angle BDE$ are supplementary. Then we know that $\angle ABD$ and $\angle AED$ are also supplementary. Given that $AE=DE$ , we can get that $\angle DAE$ is half of $\angle ABC$ . Similarly, we have $\angle DAF$ is half of $\angle ACB$ .

By applying the Law of Cosines, we get $\cos \angle ABC = \frac{1}{8}$ , and then $\sin \angle ABC = \frac{3\sqrt{7}}{8}$ . Similarly, we can get $\cos \angle ACB = \frac{3}{4}$ and $\sin \angle ACB = \frac{\sqrt{7}}{4}$ . Based on some trig identities, we can compute that $\tan \angle DAE = \frac{\sin \angle ABC}{1 + \cos \angle ABC} = \frac{\sqrt{7}}{3}$ , and $\tan \angle DAF = \frac{\sqrt{7}}{7}$ .

Finally, the area of $\triangle AEF$ equals $\frac{1}{2}AM^2(\tan \angle DAE + \tan \angle DAF)=\frac{15\sqrt{7}}{14}$ . Therefore, the final answer is $15+7+14=\boxed{036}$ . ~xamydad

Remark: I didn't figure out how to add segments $AF$ , $AE$ , $DF$ and $DE$ . Can someone please help add these segments?

(Added 🙂 ~Math_Genius_164)

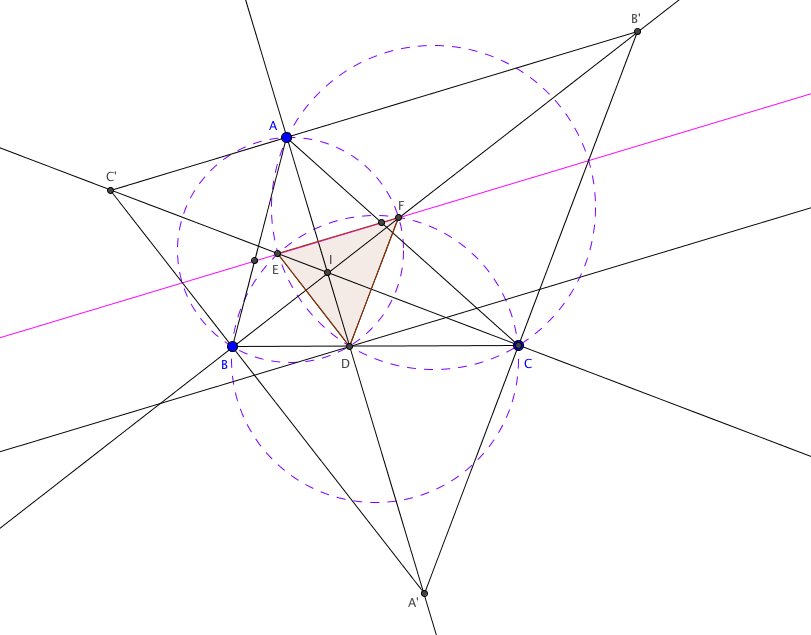
Solution 6

First and foremost $\big[\triangle{AEF}\big]=\big[\triangle{DEF}\big]$ as $EF$ is the perpendicular bisector of $AD$ . Now note that quadrilateral $ABDF$ is cyclic, because $\angle{ABF}=\angle{FBD}$ and $FA=FD$ . Similarly quadrilateral $AEDC$ is cyclic, $\implies \angle{EDA}=\dfrac{C}{2}, \quad \angle{FDA}=\dfrac{B}{2}$ Let $A'$ , $B'$ , $C'$ be the $A$ , $B$ , and $C$ excenters of $\triangle{ABC}$ respectively. Then it follows that $\triangle{DEF} \sim \triangle{A'C'B'}$ . By angle bisector theorem we have $BD=2 \implies \dfrac{ID}{IA}=\dfrac{BD}{BA}=\dfrac{1}{2}$ . Now let the feet of the perpendiculars from $I$ and $A'$ to $BC$ be $X$ and $Y$ resptively. Then by tangents we have $BX=s-AC=\dfrac{3}{2} \implies XD=2-\dfrac{3}{2}=\dfrac{1}{2}$ $CY=s-AC \implies YD=3-\dfrac{3}{2}=\dfrac{3}{2} \implies \dfrac{ID}{DA'}=\dfrac{XD}{YD}=\dfrac{1}{3} \implies \big[\triangle{DEF}\big]=\dfrac{1}{16}\big[\triangle{A'C'B'}\big]$ From the previous ratios, $AI:ID:DA'=2:1:3 \implies AD=DA' \implies \big[\triangle{ABC}\big]=\big[\triangle{A'BC}\big]$ Similarly we can find that $\big[\triangle{B'AC}\big]=2\big[\triangle{ABC}\big]$ and $\big[\triangle{C'AB}\big]=\dfrac{4}{7}\big[\triangle{ABC}\big]$ and thus $\big[\triangle{A'B'C'}\big]=\bigg(1+1+2+\dfrac{4}{7}\bigg)\big[\triangle{ABC}\big]=\dfrac{32}{7}\big[\triangle{ABC}\big] \implies \big[\triangle{DEF}\big]=\dfrac{2}{7}\big[\triangle{ABC}\big]=\dfrac{15\sqrt{7}}{14} \implies m+n+p = \boxed{036}$ -tkhalid

14.Solution 1

Either $P(3) = P(4)$ or not. We first see that if $P(3) = P(4)$ it's easy to obtain by Vieta's that $(a+b)^2 = 49$ . Now, take $P(3) \neq P(4)$ and WLOG $P(3) = P(a), P(4) = P(b)$ . Now, consider the parabola formed by the graph of $P$ . It has vertex $\frac{3+a}{2}$ . Now, say that $P(x) = x^2 - (3+a)x + c$ . We note $P(3)P(4) = c = P(3)\left(4 - 4a + \frac{8a - 1}{2}\right) \implies a = \frac{7P(3) + 1}{8}$ . Now, we note $P(4) = \frac{7}{2}$ by plugging in again. Now, it's easy to find that $a = -2.5, b = -3.5$ , yielding a value of $36$ . Finally, we add $49 + 36 = \boxed{085}$ . ~awang11, charmander3333

Remark: We know that $c=\frac{8a-1}{2}$ from $P(3)+P(4)=3+a$ .

Solution 2

Let the roots of $P(x)$ be $m$ and $n$ , then we can write $P(x)=x^2-(m+n)x+mn$ . The fact that $P(P(x))=0$ has solutions $x=3,4,a,b$ implies that some combination of $2$ of these are the solution to $P(x)=m$ , and the other $2$ are the solution to $P(x)=n$ . It's fairly easy to see there are only $2$ possible such groupings: $P(3)=P(4)=m$ and $P(a)=P(b)=n$ , or $P(3)=P(a)=m$ and $P(4)=P(b)=n$ (Note that $a,b$ are interchangeable, and so are $m$ and $n$ ). We now casework: If $P(3)=P(4)=m$ , then $9-3(m+n)+mn=16-4(m+n)+mn=m \implies m+n=7$ $a^2-a(m+n)+mn=b^2-b(m+n)+mn=n \implies a+b=m+n=7$ so this gives $(a+b)^2=7^2=49$ . Next, if $P(3)=P(a)=m$ , then $9-3(m+n)+mn=a^2-a(m+n)+mn=m \implies a+3=m+n$ $16-4(m+n)+mn=b^2-b(m+n)+mn=n \implies b+4=m+n$ Subtracting the first part of the first equation from the first part of the second equation gives $7-(m+n)=n-m \implies 2n=7 \implies n=\frac{7}{2} \implies m=-3$ Hence, $a+b=2(m+n)-7=2\cdot \frac{1}{2}-7=-6$ , and so $(a+b)^2=(-6)^2=36$ . Therefore, the solution is $49+36=\boxed{085}$ ~ktong

Solution 3

Write $P(x) = x^2+wx+z$ . Split the problem into two cases: $P(3)\ne P(4)$ and $P(3) = P(4)$ .

Case 1: We have $P(3) \ne P(4)$ . We must have $w=-P(3)-P(4) = -(9+3w+z)-(16+4w+z) = -25-7w-2z.$ Rearrange and divide through by $8$ to obtain $w = \frac{-25-2z}{8}.$ Now, note that $z = P(3)P(4) = (9+3w+z)(16+4w+z) = \left(9 + 3\cdot \frac{-25-2z}{8} + z\right)\left(16 + 4 \cdot \frac{-25-2z}{8} + z\right) =$ $\left(-\frac{3}{8} + \frac{z}{4}\right)\left(\frac{7}{2}\right) = -\frac{21}{16} + \frac{7z}{8}.$ Now, rearrange to get $\frac{z}{8} = -\frac{21}{16}$ and thus $z = -\frac{21}{2}.$ Substituting this into our equation for $w$ yields $w = -\frac{1}{2}$ . Then, it is clear that $P$ does not have a double root at $P(3)$ , so we must have $P(a) = P(3)$ and $P(b) = P(4)$ or vice versa. This gives $3+a = \frac{1}{2}$ and $4+b = \frac{1}{2}$ or vice versa, implying that $a+b = 1-3-4 = -6$ and $(a+b)^2 = 6$ .

Case 2: We have $P(3) = P(4)$ . Then, we must have $w = -7$ . It is clear that $P(a) = P(b)$ (we would otherwise get $P(a)=P(3)=P(4)$ implying $a \in \{3,4\}$ or vice versa), so $a+b=-w=7$ and $(a+b)^2 = 49$ .

Thus, our final answer is $49+36=\boxed{085}$ . ~GeronimoStilton

Solution 4

Let $P(x)=(x-r)(x-s)$ . There are two cases: in the first case, $(3-r)(3-s)=(4-r)(4-s)$ equals $r$ (without loss of generality), and thus $(a-r)(a-s)=(b-r)(b-s)=s$ . By Vieta's formulas $a+b=r+s=3+4=7$ .

In the second case, say without loss of generality $(3-r)(3-s)=r$ and $(4-r)(4-s)=s$ . Subtracting gives $-7+r+s=r-s$ , so $s=7/2$ . From this, we have $r=-3$ .

Note $r+s=1/2$ , so by Vieta's, we have $\{a,b\}=\{1/2-3,1/2-4\}=\{-5/2,-7/2\}$ . In this case, $a+b=-6$ .

The requested sum is $36+49=85$ .~TheUltimate123

15.Solution 1

The following is a power of a point solution to this menace of a problem: $[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */ import graph; size(18cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -12.821705655137235, xmax = 10.870448356581754, ymin = -3.0673360097491003, ymax = 10.363346102088961; /* image dimensions */ pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); /* draw figures */ draw((xmin, 0.0052470390246834855*xmin + 3.437118410441658)--(xmax, 0.0052470390246834855*xmax + 3.437118410441658), linewidth(2) + wrwrwr); /* line */ draw(circle((-4.538171990791266,4.905585481447388), 4.693275552848494), linewidth(2) + wrwrwr); draw(circle((-4.522512329243054,1.9211095752183682), 4.693275552848494), linewidth(2) + wrwrwr); draw((xmin, -190.58367877496823*xmin-1479.5139994609244)--(xmax, -190.58367877496823*xmax-1479.5139994609244), linewidth(2) + wrwrwr); /* line */ draw((xmin, 0.9703333412757664*xmin + 12.849035992754926)--(xmax, 0.9703333412757664*xmax + 12.849035992754926), linewidth(2) + wrwrwr); /* line */ draw(circle((-7.790821079477277,5.289342543424063), 1.8930768158550504), linewidth(2) + wrwrwr); draw((xmin, -1.0305736775830343*xmin-5.438100054565965)--(xmax, -1.0305736775830343*xmax-5.438100054565965), linewidth(2) + wrwrwr); /* line */ draw((xmin, -1.0305736775830343*xmin + 0.22866488339331612)--(xmax, -1.0305736775830343*xmax + 0.22866488339331612), linewidth(2) + wrwrwr); /* line */ /* dots and labels */ dot((-8.98,3.39),dotstyle); label("$B$", (-8.914038694762803,3.548005694821766), NE * labelscalefactor); dot((-0.08068432003432058,3.4366950566657577),dotstyle); label("$C$", (-0.021788682572170717,3.594159241597842), NE * labelscalefactor); dot((-4.538171990791266,4.905585481447388),dotstyle); label("$O$", (-4.483298204259513,5.055688222840243), NE * labelscalefactor); dot((-4.522512329243054,1.9211095752183682),linewidth(4pt) + dotstyle); label("$O'$", (-4.467913688667488,2.0403231668032897), NE * labelscalefactor); dot((-7.790821079477277,5.289342543424063),dotstyle); label("$H$", (-7.729430994176854,5.440301112640874), NE * labelscalefactor); dot((-7.806480741025488,8.273818449653083),linewidth(4pt) + dotstyle); label("$A$", (-7.7448155097688804,8.394128106309726), NE * labelscalefactor); dot((-9.139423209055858,3.980748932978468),linewidth(4pt) + dotstyle); label("$X$", (-9.083268366275083,4.101848256134676), NE * labelscalefactor); dot((-9.752410287411378,3.3859471330788855),linewidth(4pt) + dotstyle); label("$K$", (-9.68326447436407,3.5018521480456903), NE * labelscalefactor); dot((-3.475227037470366,9.476907329794422),linewidth(4pt) + dotstyle); label("$Y$", (-3.4063821128177407,9.594120322487697), NE * labelscalefactor); dot((-7.780888168280388,3.3962917865759925),linewidth(4pt) + dotstyle); label("$L$", (-7.714046478584829,3.5172366636377155), NE * labelscalefactor); dot((-7.776585346090923,2.5762441045932913),linewidth(4pt) + dotstyle); label("$D$", (-7.714046478584829,2.7018573372603765), NE * labelscalefactor); dot((-6.307325123263112,6.728828131386446),linewidth(4pt) + dotstyle); label("$E$", (-6.252517497342424,6.855676547107199), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]$

Let points be what they appear as in the diagram below. Note that $3HX = HY$ is not insignificant; from here, we set $XH = HE = \frac{1}{2} EY = HL = 2$ by PoP and trivial construction. Now, $D$ is the reflection of $A$ over $H$ . Note $AO \perp XY$ , and therefore by Pythagorean theorem we have $AE = XD = \sqrt{5}$ . Consider $HD = 3$ . We have that $\triangle HXD \cong HLK$ , and therefore we are ready to PoP with respect to $(BHC)$ . Setting $BL = x, LC = y$ , we obtain $xy = 10$ by PoP on $(ABC)$ , and furthermore, we have $KH^2 = 9 = (KL - x)(KL + y) = (\sqrt{5} - x)(\sqrt{5} + y)$ . Now, we get $4 = \sqrt{5}(y - x) - xy$ , and from $xy = 10$ we take $\frac{14}{\sqrt{5}} = y - x.$ However, squaring and manipulating with $xy = 10$ yields that $(x + y)^2 = \frac{396}{5}$ and from here, since $AL = 5$ we get the area to be $3\sqrt{55} \implies \boxed{058}$ . ~awang11's sol

Solution 1a

As in the diagram, let ray $AH$ extended hits BC at L and the circumcircle at say $P$ . By power of the point at H, we have $HX \cdot HY = AH \cdot HP$ . The three values we are given tells us that $HP=\frac{2\cdot 6}{3}=4$ . L is the midpoint of $HP$ (see here: https://www.cut-the-knot.org/Curriculum/Geometry/AltitudeAndCircumcircle.shtml ), so $HL=LP=2$ .

As in the diagram provided, let K be the intersection of $BC$ and $XY$ . By power of a point on the circumcircle of triangle $HBC$ , $KH^{2}=KB \cdot KC$ . By power of a point on the circumcircle of triangle $ABC$ , $KB \cdot KC=KX \cdot KY$ , thus $KH^{2}=(KH-2)(KH+6)$ . Solving gives $4KH=12$ or $KH=3$ .

By the Pythagorean Theorem on triangle $HKL$ , $KL=\sqrt{5}$ . Now continue with solution 1.

Solution 2

$[asy] size(10cm); pair A, B, C, D, H, K, O, P, L, M, X, Y; A = (-15, 27); B = (-24, 0); C = (24, 0); D = (-8.28, 18.04); O = (0, 7); P = (0, -7); H = (-15, 13); K = (-15, -13); M = (0, 0); L = (-15, 0); X = (-24.9569, 5.53234); Y = (8.39688, 30.5477); draw(circle(O, 25)); draw(circle(P, 25)); draw(A--B--C--cycle); draw(H -- K); draw(A -- O -- P -- H -- cycle); draw(X -- Y); draw(O -- X, dashed); draw(O -- Y, dashed); draw(O -- B, dashed); draw(O -- C, dashed); label("$O$", O, ENE); label("$A$", A, NW); label("$B$", B, W); label("$C$", C, E); label("$H$", H, E); label("$H'$", K, NE); label("$X$", X, W); label("$Y$", Y, NE); label("$O'$", P, E); label("$M$", M, NE); label("$L$", L, NE); label("$D$", D, NNE); label("$2$", X -- H, NW); label("$3$", H -- A, SW); label("$6$", H -- Y, NW); label("$R$", O -- Y, E); dot(O); dot(P); dot(D); dot(H); [/asy]$ Diagram not to scale.

We first observe that $H'$ , the image of the reflection of $H$ over line $BC$ , lies on circle $O$ . This is because $\angle HBC = 90 - \angle C = \angle H'AC = \angle H'BC$ . This is a well known lemma. The result of this observation is that circle $O'$ , the circumcircle of $\triangle BHC$ is the image of circle $O$ over line $BC$ , which in turn implies that $\overline{AH} = \overline{OO'}$ and thus $AHO'O$ is a parallelogram. That $AHO'O$ is a parallelogram implies that $AO$ is perpendicular to $\overline{XY}$ , and thus divides segment $\overline{XY}$ in two equal pieces, $\overline{XD}$ and $\overline{DY}$ , of length $4$ .

Using Power of a Point, $\overline{AH} \cdot \overline{HH'} = \overline{XH} \cdot \overline{HY} \Longrightarrow 3 \cdot \overline{HH'} = 2 \cdot 6 \Longrightarrow \overline{HH'} = 4$ This means that $\overline{HL} = \frac12 \cdot 4 = 2$ and $\overline{AL} = 2 + 3 = 5$ , where $L$ is the foot of the altitude from $A$ onto $BC$ . All that remains to be found is the length of segment $\overline{BC}$ .

Looking at right triangle $\triangle AHD$ , we find that $\overline{AD} = \sqrt{\overline{AH}^2 - \overline{HD}^2} = \sqrt{3^2 - 2^2} = \sqrt{5}$ Looking at right triangle $\triangle ODY$ , we get the equation $\overline{OY}^2 - \overline{DY}^2 = \overline{OD}^2 = \left(\overline{AO} - \overline{AD}\right)^2$ Plugging in known values, and letting $R$ be the radius of the circle, we find that $R^2 - 16 = (R - \sqrt{5})^2 = R^2 - 2\sqrt5 R + 5 \Longrightarrow R = \frac{21\sqrt5}{10}$

Recall that $AHO'O$ is a parallelogram, so $\overline{AH} = \overline{OO'} = 3$ . So, $\overline{OM} = \frac32$ , where $M$ is the midpoint of $\overline{BC}$ . This means that $\overline{BC} = 2\overline{BM} = 2\sqrt{R^2 - \left(\frac32\right)^2} = 2\sqrt{\frac{441}{20} - \frac{9}{4}} = \frac{6\sqrt{55}}{5}$

Thus, the area of triangle $\triangle ABC$ is $\frac{\overline{AL} \cdot \overline{BC}}{2} = \frac{5 \cdot \frac{6\sqrt{55}}{5}}{2} = {3\sqrt{55}}$ The answer is $3 + 55 = \boxed{058}$ .