2018 AIO(Intermediate) 赛题

2018 AIO(Intermediate) 赛题

Street Construction

Input File: streetin.txt
Output File: streetout.txt
Time Limit: 1 second
Memory Limit: 1 GB

The great city of Dubvegas is designing one side of a new street. This street is divided into evenly sized chunks of land, each of which will be used for either a house or a park. The city takes great pride in both the number of parks that it has, and that no one has to walk far to reach one of their wonderful parks.

In particular, the city calls a group of consecutive houses a `block'. The size of a block is the number of houses it contains.

You must determine, given the number of chunks of land on the street and the number of parks that will be built, the minimum possible size of the largest block.

Input

The only line will contain the number of chunks of land N on the street, followed by the number of parks that will be built K.

Output

Your program should output the minimum possible size of the largest block on a street with N chunks of land, where K parks will be built.

Castle Cavalry

Input File: cavalryin.txt
Output File: cavalryout.txt
Time Limit: 1 second
Memory Limit: 1 GB

As the Queen's chief technologist, you have been tasked with organising the army's newest cutting edge¹ division: the cavalry.

Naturally, the Queen is sceptical, so to prove it's worth it you are going to conduct a quick field test. Firstly, you will need to group your knights into squads.

Unfortunately, the N knights in your division are very inexperienced, having only been training for two weeks! The ith knight (counting from 1) has told you that they would only be comfortable in a squad containing exactly a_i knights.

You can make as many or as few squads as you like of any size, so long as every knight is comfortable.

After feeding your whining, whinnying horses their pheasant-based supper, you return to your lonely lodge to determine if it is possible to divide up your cavalry.

Input

The first line of input will contain N, the number of knights in your division.

Then, N lines will follow. The ith line (counting from 1) will contain a_i, the size of the squad the ith knight wants to join.

Output

Print YES on a single line if it is possible to put the knights into squads such that they are all comfortable. If it is not possible, then print NO instead.

Cloud Coverage

Input File: cloudin.txt
Output File: cloudout.txt
Time Limit: 1 second
Memory Limit: 1 GB

During lunch you and your friends were playing your favourite game `stand along a line' when a huge cloud blew overhead. So you got to wondering, how long could that cloud have been? You immediately noted down how far apart each of your friends were standing from one another along the line, and the maximum number that were simultaneously underneath the cloud.

Note that if two people are exactly separated by the length of the cloud, then only one of them can be covered by the cloud at a time. Thus if a cloud is 5 metres long, and two people are standing 5 metres apart, the cloud is only able to cover one of them at a time.

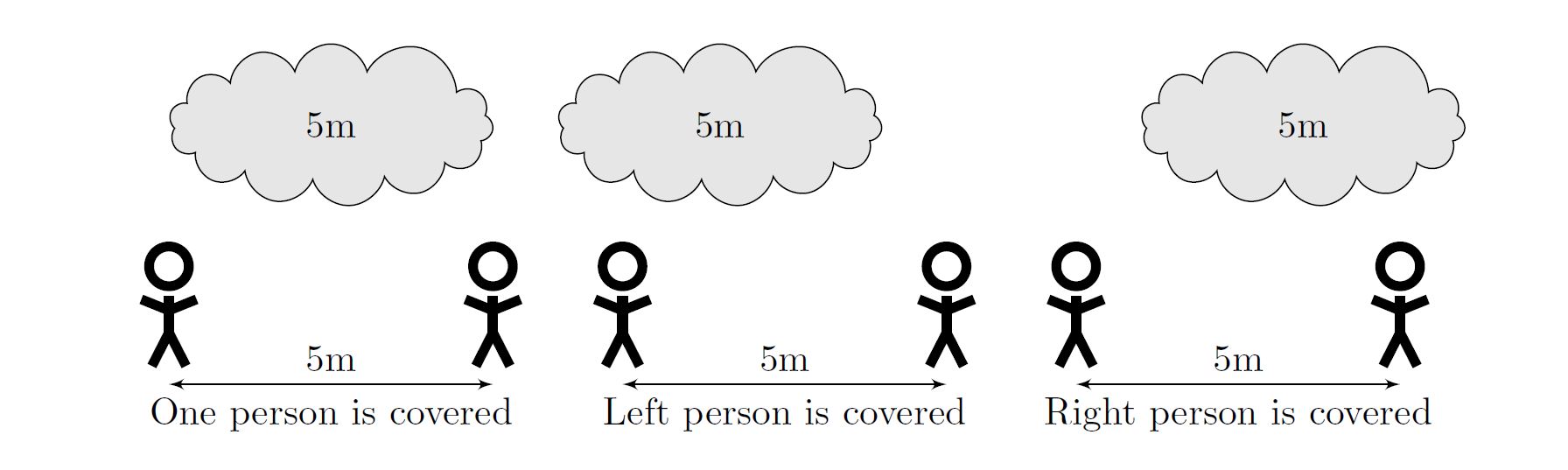
You must now determine the maximum length the cloud could have been, taking into account the maximum number of people it covered simultaneously.

Input

The first line will contain the number of people standing along the line, N, followed by the maximum number covered at any time by the cloud K.

The following N-1 lines contain the successive distances between the N people playing the game. These will always be integers.

Output

The maximum length the cloud could have been given that it never covered more than K of your N friends.

Janitor

Input File: janitorin.txt
Output File: janitorout.txt
Time Limit: 1 second
Memory Limit: 1 GB

Congratulations! You have been appointed head bathroom janitor of your school! Okay, okay, I know you're not thrilled, but somebody has to do it. We thank you for your sacrifice.

The bathroom floor is covered in a rectangular grid of tiles. No one is watching you very closely, so pouring a bucket of water over the floor is enough to make it look like you cleaned it. There is one small problem. The floor is uneven, so depending on which tile you pour the water on, some tiles may not become wet at all, and your deception will be exposed.

Water can flow from any square to any adjacent square of lower height, where adjacent squares may be to the north, south, east or west (water cannot flow across diagonals).

To finish your chore as soon as possible, you've decided to find out what is the fewest number of tiles you need to pour water on to make sure every tile becomes wet.

To complicate matters further, the bathroom is undergoing some hasty renovations. Each day, a tradie will replace one of the tiles, changing its height. After each replacement, you will need to figure out again how many tiles you need to pour water on.

Input

• The first line of input contains three space-separated integers, R, C, and Q. There are R rows and C columns of tiles and there will be Q replacements made by the tradies.
• The next R lines each contain C space-separated integers, giving the initial heights of the tiles. The tradie did such a terrible job at tiling the bathroom that literally no two adjacent tiles have the same height, even after any replacements.
• The following Q lines each contain three integers r_i, c_i and h_i. This indicates that the tradies have replaced the tile situated in row r_i and column c_i with a tile of height h_i. Rows are labelled from 1 to R (from top to bottom) and columns are labelled from 1 to C (from left to right).

Output

The output should contain Q+1 lines. The first line should contain the fewest tiles you need to pour water on to make sure every tile gets wet before any replacements are made. The next Q lines should correspond to the Q tile replacements. After each replacement has been made (including all previous modifications), your program should write one line containing the fewest tiles you need to pour water on to make sure every tile gets wet.