霸气外露！翰林参考学员AIME晋级率高达90.9%！内附AMC最新备赛课程及福利

01学术活动年龄阶段规划

打好基础，冲刺牛剑藤校的必备申请战绩。我们建议数学感兴趣的学生，在不同年龄段的规划一路升级打怪如下⬇⬇⬇

3-12年级：Math league

6-8年级：AMC8 and AMC10（考试时间不冲突，推荐同时备考）

8-10年级：AMC10 or AMC12（考试时间冲突，选择性备考）

11-12年级：AMC12

10-12年级AMC10/12晋级学员：AIME

02翰林金牌学术活动体系课程

Math League 备赛班	上课时间	课时
小学组 （3-6年级）	3/18-8/1  每周六18:00-20:00	40h
初中组 （6-9年级）	3/19-8/2  每周日18:00-20:00	40h

AMC 金牌辅导课程	上课时间	课时
AMC全程班	全年滚动开课	60h
AMC8&10&12 基础班	3月14日-7月25日 每周六10:00-12:00	40h
AMC8&10&12 强化班	3月15日-7月26日 每周日10:00-12:00	40h
AMC8强化班	7月27日-8月21日 10:00-12:00	40h
AMC10强化班	7月27日-8月21日 13:00-15:00	40h
AMC12强化班	7月27日-8月21日 17:00-19:00	40h
AMC冲刺班 （临近考试）	赛前2个月内	40h

需要最合适你的学术活动路线吗 

带你打最热门的国际学术活动 · 拿最高分 

03翰林AMC最新课程大纲

全新设计的AMC班

分级难度，循序渐进，高效备赛

AMC8 基础班

Number theory

Even and odd

Prime and composite

Prime factorization

Number of factors

Algebra

Positive and negative number

Operations with fractions

Terminating decimals and repeating decimals

Converting repeating decimals to fractions

Operations of irrational numbers

linear equations

Linear inequations and system of linear inequations

Functions

Words problem related to percents

Geometry

Lines (line segments, straight lines, radial lines)

Angles (acute angles, obtuse angles, straight angles, round angles, vertical angles,

complementary angles, supplementary angles)

Relationship of angles formed by parallel lines

Triangles (acute triangles, obtuse triangles, right triangles, perimeter, area)

Pythagorean theorem

Properties of isosceles triangles and equilateral triangles

Probability and Statistic

Statistics (average numbers, mode, median, variance, standard deviation, range, graphs)

Sum rules and product rules

AMC8 提高班

Number theory

Divisibility rules

Base-n representation

Gaussian function

Algebra

Arithmetic and geometric sequences

System of linear equation and nonlinear equation

quadratic equations

Estimation of arithmetic, exponent and radical

Special symbols and operations

Geometry

Congruent triangles (principles and properties)

Similar triangles (principles and properties)

Quadrilaterals (rectangles, squares, parallelograms, rhombuses, trapezoids)

Polygons

Circles (chord, diameter, radius, tangent)

Coordinates

Transformations (symmetry, translation, rotation, folding)

Solid geometry

Probability and Statistic

Pigeonhole principle

Grouping

Number of arrangement and combination

Classical probability and geometric probability

AMC10 基础班

1.Number theory

Even and odd，Prime and composite

Prime factorization and Basic theorem of Arithmetic.

Number of factors

Lcm and Gcd

Divisibility rules

2.Algebra

Algebraic operation

linear equations and quadratic equations

Linear inequations and system of linear inequations

System of linear equation and nonlinear equation

3.Geometry

Lines (line segments, straight lines, radial lines)

Angles (acute angles, obtuse angles, straight angles, round angles, vertical angles,

complementary angles, supplementary angles)

Relationship of angles formed by parallel lines

Triangles (acute triangles, obtuse triangles, right triangles, perimeter, area)

Special triangles

Congruent triangles and Similar triangles (principles and properties)

Quadrilaterals

Polygons

4.Probability and Statistic

Statistics (average numbers, mode, median, variance, standard deviation, range, graphs)

Sum rules and product rules

Logic reasoning

Permutations and Combinations

Elementary probability

AMC10 提高班

1.Number theory

Character of digits

Base-n representation

Gaussian function

Remainder theorem

Euler’s function and theorem

Fermat’s little theorem

2.Algebra

Arithmetic and geometric sequences

Recursive sequence

Exponent and radical

Special symbols and operations

Vieta’s theorem

Functions

3.Geometry

Circles (chord, diameter, radius, tangent, secant, minor arc, major arc, perimeter, area, central

angles, circular sector)

Transformations (symmetry, translation, rotation, folding)

Solid geometry

Volumes (rectangular solid, cylinder, sphere, cone, pyramid)

Euler’s formulas

Sets and Venn diagrams

Coordinates Geometry(lines and circles)

4.Probability and Statistic

Pigeonhole principle

Advanced permutations

Advanced combinations

Binomial theorem

Classical probability and Geometric probability

AMC12 基础班

1.Number theory

Prime factorization and Basic theorem of Arithmetic.

Divisibility rules

Number of factors

Lcm and Gcd

Character of digit and Base-n representation

Remainder theorem

Gaussian function

2.Algebra

Linear equations and quadratic equations(vieta’s theorem of higher degree equations )

Linear inequations and system of linear inequations

System of linear equation and nonlinear equation

Functions

Exponent and radical

Polynomial

3.Geometry

Triangles (acute triangles, obtuse triangles, right triangles, perimeter, area)

Special triangles(Right triangles,Isosceles triangle,Equilateral triangle)

Congruent triangles and Similar triangles (principles and properties)

Quadrilaterals

Polygons

4.Probability and Statistic

Statistics (average numbers, mode, median, variance, standard deviation, range, graphs)

Sum rules and product rules

Logic reasoning

Binomial theorem

Permutations and Combinations

Elementary probability

AMC12 提高班

1.Number theory

Gaussian function

Euler’s function and theorem

Fermat’s little theorem

Complex number

2.Algebra

Arithmetic and geometric sequences

Recursive sequence

AM-GM inequality

Trigonometry six functions

Operations of complex number

3.Geometry

Circles (chord, diameter, radius, tangent, secant, minor arc, major arc, perimeter, area, central

angles, circular sector)

Transformations (symmetry, translation, rotation, folding)

Solid geometry

Volumes (rectangular solid, cylinder, sphere, cone, pyramid)

Euler’s formulas

Sets and Venn diagrams

Analytical Geometry(lines and circles)

4.Probability and Statistic

Pigeonhole principle

Advanced permutations

Advanced combinations

Classical probability and Geometric probability

04翰林首席🏅导师介绍

翰林 Z老师

◆清华大学直博，擅长数学和化学课程的教学，曾荣获英国皇家化学会RSC最佳口头报告奖、美国数学建模学术活动MCM/ICM全球一等奖、MathorCup数学建模挑战赛全国特等奖等国际级、国家级、省市级85项奖。

◆授课幽默风趣、通俗易懂。同时注重知识点的拓展延伸，激发学生的学习兴趣。

◆多次指导学生参加学科学术活动，例如：主授AMC/Mathlegue系列、MCM等，曾指导学生参加2018年丘成桐中学科学奖（经济金融建模）比赛，荣获分赛区决赛二等奖，以及2018年美国高中生数学建模学术活动（HiMCM）比赛。2019年辅导翰林mathleague学员晋级率90%

翰林 C老师

◆英国雷丁大学教育学硕士，具有丰富的教育学背景，曾在国内激光杂志上发表过论文。课堂教学过程中注重知识点结合实际生活中的运用，激发学生的学习热情。

◆主要负责Mathlegue/IGCSE, a-level/IB数学以及物理的教学，学生大多被美国及英国top50的学校录取。同时还可以进行国际学校择校备考的教学，所教授的学生均被平和，领科等上海老牌国际学校录取。

◆2019年辅导Mathleague小班，学员全部晋级。

翰林 G老师

◆布里斯托大学应用数学硕博，高考数学148分，国内数学物理学术活动背景，曾负责国内一线机构AMC项目研发和教师培训，曾担任国内知名高中国际部数学老师/学术活动教练。

◆2017年12月在上海完成两个AMC10/12考前冲刺班培训，18名学员9人进入AIME。2018年担任上海翰林学员AMC/AIME小班课程导师，精英小班全部学员晋级AIME。

翰林 Z老师

◆美国罗切斯特大学理论数学博士（硕博连读），复旦大学上海数学中心博士后研究员，5年海外留学经验，7年理论数学的研究与相关教学经验。主要研究领域为分析与非线性波动方程，博士与博士后阶段研究了量子场论背景的Skyrme-Faddeev方程与极小曲面方程，并得到了很好的正则适定型结果。

◆具有丰富的美国学习、生活、与科研工作经验，曾多次参加美国、欧洲的各种学术交流会议。教学背景方面，在博士与博士后阶段每年都有大量学校的数学课程教学任务（主要为大学微积分、线性代数以及数学系的相关专业习题课课程），

◆同时曾多次参与了Rochester当地中小学与大学学术活动的培训与讲座工作（博士阶段导师曾经为罗马尼亚IMO代表队成员，现为Rochester当地学术活动总教练）。

翰林 Y老师

◆翰林AMC课程主管，985本科获得直博名额，举办多次校级学术活动，两次市级学术活动；6年教学经验，AMC8、AMC10教师；某知名国际学校学术活动班集训课教师，学生多人晋级AIME。

◆2018年“哈佛班”数学授课教师（五名学员，平和、世外、星河湾各录取一名，领科录取两名）；

◆2019年辅导22名学员晋级AMC8 全球前5%，最高分24分；

◆2018-2019年度AMC10B辅导最高分136.5分；

◆2019年math league学员均晋级。

05赠送最新AMC8-12精编习题册

比AOPS更精细排版更全更好

翰林耗时耗力精心编排 

AMC历年真题手册(含2020题) 

免费送！送！送！送到家！

最真实的AMC考场答题卡 - 翰林为你复制出最逼近的答题卡，让你提早感受适应答题状态。

相较于网上流传售卖的错误百出的AMC真题册，翰林版AMC历年真题阅读视觉效果更佳，所有的公式字符均校对重新排版。题目准确率高，真实还原真题，内容全面轻松备考。

翰林最早整理了AMC网页版的真题，而且访问速度是全网最快，大大优于AOPS原站。

学术活动报名扫码了解！免费领取历年真题！

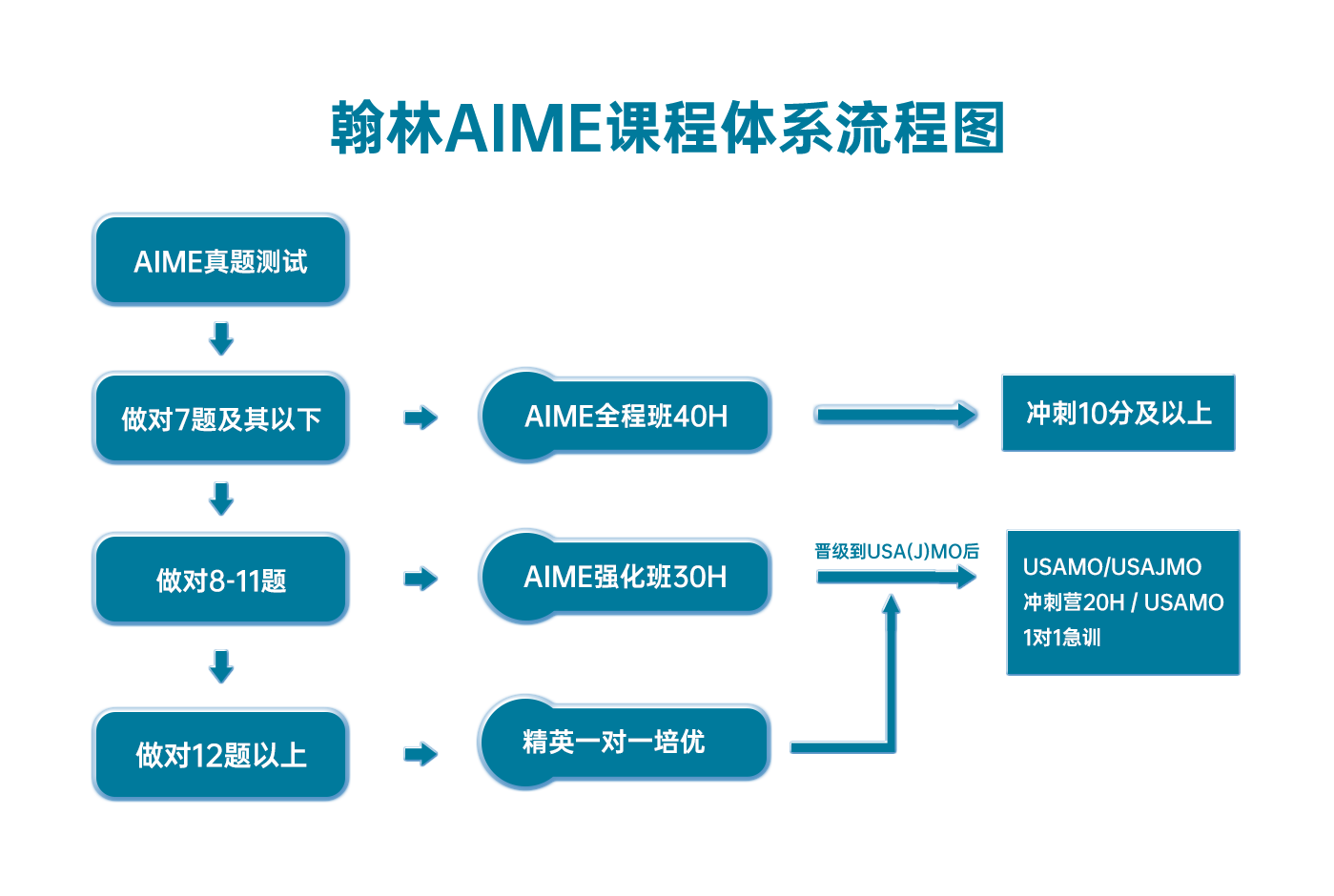
翰林AIME课程体系流程图