- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1985AIME 真题及答案解析
1985AIME 真题及答案解析
答案解析请参考文末
Problem 1
Let ![]() , and for
, and for ![]() let
let ![]() . Calculate the product
. Calculate the product ![]() .
.
Problem 2
When a right triangle is rotated about one leg, the volume of the cone produced is ![]() . When the triangle is rotated about the other leg, the volume of the cone produced is
. When the triangle is rotated about the other leg, the volume of the cone produced is ![]() . What is the length (in cm) of the hypotenuse of the triangle?
. What is the length (in cm) of the hypotenuse of the triangle?
Problem 3
Find ![]() if
if ![]() ,
, ![]() , and
, and ![]() are positive integers which satisfy
are positive integers which satisfy ![]() , where
, where ![]() .
.
Problem 4
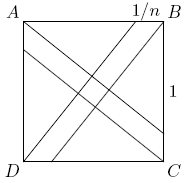
A small square is constructed inside a square of area ![]() by dividing each side of the unit square into
by dividing each side of the unit square into ![]() equal parts, and then connecting the vertices to the division points closest to the opposite vertices, as shown in the figure. Find the value of
equal parts, and then connecting the vertices to the division points closest to the opposite vertices, as shown in the figure. Find the value of ![]() if the the area of the small square is exactly
if the the area of the small square is exactly ![]() .
. 
Problem 5
A sequence of integers ![]() is chosen so that
is chosen so that ![]() for each
for each ![]() . What is the sum of the first
. What is the sum of the first ![]() terms of this sequence if the sum of the first
terms of this sequence if the sum of the first ![]() terms is
terms is ![]() , and the sum of the first
, and the sum of the first ![]() terms is
terms is ![]() ?
?
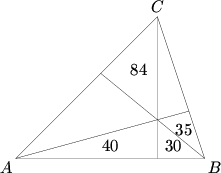
Problem 6
As shown in the figure, ![]() is divided into six smaller triangles by lines drawn from the vertices through a common interior point. The areas of four of these triangles are as indicated. Find the area of
is divided into six smaller triangles by lines drawn from the vertices through a common interior point. The areas of four of these triangles are as indicated. Find the area of ![]() .
. 
Problem 7
Assume that ![]() ,
, ![]() ,
, ![]() and
and ![]() are positive integers such that
are positive integers such that ![]() ,
, ![]() and
and ![]() . Determine
. Determine ![]() .
.
Problem 8
The sum of the following seven numbers is exactly 19: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . It is desired to replace each
. It is desired to replace each ![]() by an integer approximation
by an integer approximation ![]() ,
, ![]() , so that the sum of the
, so that the sum of the ![]() 's is also
's is also ![]() and so that
and so that ![]() , the maximum of the "errors"
, the maximum of the "errors" ![]() , is as small as possible. For this minimum
, is as small as possible. For this minimum ![]() , what is
, what is ![]() ?
?
Problem 9
In a circle, parallel chords of lengths ![]() ,
, ![]() , and
, and ![]() determine central angles of
determine central angles of ![]() ,
, ![]() and
and ![]() radians, respectively, where
radians, respectively, where ![]() . If
. If ![]() , which is a positive rational number, is expressed as a fraction in lowest terms, what is the sum of its numerator and denominator?
, which is a positive rational number, is expressed as a fraction in lowest terms, what is the sum of its numerator and denominator?
Problem 10
How many of the first ![]() positive integers can be expressed in the form
positive integers can be expressed in the form ![]() ,
,
where ![]() is a real number, and
is a real number, and ![]() denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to ![]() ?
?
Problem 11
An ellipse has foci at ![]() and
and ![]() in the
in the ![]() -plane and is tangent to the
-plane and is tangent to the ![]() -axis. What is the length of its major axis?
-axis. What is the length of its major axis?
Problem 12
Let ![]() ,
, ![]() ,
, ![]() and
and ![]() be the vertices of a regular tetrahedron, each of whose edges measures
be the vertices of a regular tetrahedron, each of whose edges measures ![]() meter. A bug, starting from vertex
meter. A bug, starting from vertex ![]() , observes the following rule: at each vertex it chooses one of the three edges meeting at that vertex, each edge being equally likely to be chosen, and crawls along that edge to the vertex at its opposite end. Let
, observes the following rule: at each vertex it chooses one of the three edges meeting at that vertex, each edge being equally likely to be chosen, and crawls along that edge to the vertex at its opposite end. Let ![]() be the probability that the bug is at vertex
be the probability that the bug is at vertex ![]() when it has crawled exactly
when it has crawled exactly ![]() meters. Find the value of
meters. Find the value of ![]() .
.
Problem 13
The numbers in the sequence ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() are of the form
are of the form ![]() , where
, where ![]() . For each
. For each ![]() , let
, let ![]() be the greatest common divisor of
be the greatest common divisor of ![]() and
and ![]() . Find the maximum value of
. Find the maximum value of ![]() as
as ![]() ranges through the positive integers.
ranges through the positive integers.
Problem 14
In a tournament each player played exactly one game against each of the other players. In each game the winner was awarded 1 point, the loser got 0 points, and each of the two players earned ![]() point if the game was a tie. After the completion of the tournament, it was found that exactly half of the points earned by each player were earned in games against the ten players with the least number of points. (In particular, each of the ten lowest scoring players earned half of her/his points against the other nine of the ten). What was the total number of players in the tournament?
point if the game was a tie. After the completion of the tournament, it was found that exactly half of the points earned by each player were earned in games against the ten players with the least number of points. (In particular, each of the ten lowest scoring players earned half of her/his points against the other nine of the ten). What was the total number of players in the tournament?
Problem 15
Three ![]() cm
cm ![]() cm squares are each cut into two pieces
cm squares are each cut into two pieces ![]() and
and ![]() , as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in
, as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in ![]() ) of this polyhedron?
) of this polyhedron? 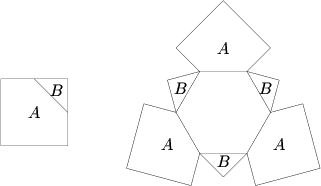
1985AIME 详细解析
- Since
 ,
,  . Setting
. Setting  and
and  in this equation gives us respectively
in this equation gives us respectively  ,
,  ,
,  and
and  so
so![[x_1x_2x_3x_4x_5x_6x_7x_8 = 2cdot4cdot6cdot8 = boxed{384}.]](https://latex.artofproblemsolving.com/d/c/5/dc517b8bd93adf1e5d719d491779824034848b4b.png) Notice that the value of
Notice that the value of  was completely unneeded!
was completely unneeded! - Let one leg of the triangle have length
 and let the other leg have length
and let the other leg have length  . When we rotate around the leg of length
. When we rotate around the leg of length  , the result is a cone of height
, the result is a cone of height  and radius
and radius  , and so of volume
, and so of volume  . Likewise, when we rotate around the leg of length
. Likewise, when we rotate around the leg of length  we get a cone of height
we get a cone of height  and radius
and radius  and so of volume
and so of volume  . If we divide this equation by the previous one, we get
. If we divide this equation by the previous one, we get  , so
, so  . Then
. Then  so
so  and
and  so
so  . Then by the Pythagorean Theorem, the hypotenuse has length
. Then by the Pythagorean Theorem, the hypotenuse has length  .
. - Expanding out both sides of the given equation we have
 . Two complex numbers are equal if and only if their real parts and imaginary parts are equal, so
. Two complex numbers are equal if and only if their real parts and imaginary parts are equal, so  and
and  . Since
. Since  are integers, this means
are integers, this means  is a divisor of 107, which is a prime number. Thus either
is a divisor of 107, which is a prime number. Thus either  or
or  . If
. If  ,
,  so
so  , but
, but  is not divisible by 3, a contradiction. Thus we must have
is not divisible by 3, a contradiction. Thus we must have  ,
,  so
so  and
and  (since we know
(since we know  is positive). Thus
is positive). Thus  .
. - The lines passing through
 and
and  divide the square into three parts, two right triangles and a parallelogram. Using the smaller side of the parallelogram,
divide the square into three parts, two right triangles and a parallelogram. Using the smaller side of the parallelogram,  , as the base, where the height is 1, we find that the area of the parallelogram is
, as the base, where the height is 1, we find that the area of the parallelogram is  . By the Pythagorean Theorem, the longer base of the parallelogram has length
. By the Pythagorean Theorem, the longer base of the parallelogram has length  , so the parallelogram has height
, so the parallelogram has height  . But the height of the parallelogram is the side of the little square, so
. But the height of the parallelogram is the side of the little square, so  . Solving this quadratic equation gives
. Solving this quadratic equation gives  .
.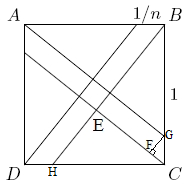 Surrounding the square with area
Surrounding the square with area  are
are  right triangles with hypotenuse
right triangles with hypotenuse  (sides of the large square). Thus,
(sides of the large square). Thus,  , where
, where  is the area of the of the 4 triangles. We can thus use proportions to solve this problem.
is the area of the of the 4 triangles. We can thus use proportions to solve this problem. Also,
Also, Thus,
Thus, Simple factorization and guess and check gives us
Simple factorization and guess and check gives us  .
. - The problem gives us a sequence defined by a recursion, so let's calculate a few values to get a feel for how it acts. We aren't given initial values, so let
 and
and  . Then
. Then  ,
,  ,
,  ,
,  ,
,  and
and  . Since the sequence is recursively defined by the first 2 terms, after this point it must continue to repeat. Thus, in particular
. Since the sequence is recursively defined by the first 2 terms, after this point it must continue to repeat. Thus, in particular  for all
for all  , and so repeating this
, and so repeating this  times,
times,  for all integers
for all integers  and
and  .Because of this, the sum of the first 1492 terms can be greatly simplified:
.Because of this, the sum of the first 1492 terms can be greatly simplified:  is the largest multiple of 6 less than 1492, so
is the largest multiple of 6 less than 1492, so  , where we can make this last step because
, where we can make this last step because  and so the entire second term of our expression is zero.Similarly, since
and so the entire second term of our expression is zero.Similarly, since  ,
,  .Finally,
.Finally,  .Then by the givens,
.Then by the givens,  and
and  so
so  and so the answer is
and so the answer is  .
. - Let the interior point be
 , let the points on
, let the points on  ,
,  and
and  be
be  ,
,  and
and  , respectively. Let
, respectively. Let  be the area of
be the area of  and
and  be the area of
be the area of  . Note that
. Note that  and
and  share the same altitude from
share the same altitude from  , so the ratio of their areas is the same as the ratio of their bases. Similarly,
, so the ratio of their areas is the same as the ratio of their bases. Similarly,  and
and  share the same altitude from
share the same altitude from  , so the ratio of their areas is the same as the ratio of their bases. Moreover, the two pairs of bases are actually the same, and thus in the same ratio. As a result, we have:
, so the ratio of their areas is the same as the ratio of their bases. Moreover, the two pairs of bases are actually the same, and thus in the same ratio. As a result, we have:  or equivalently
or equivalently  and so
and so  .Applying identical reasoning to the triangles with bases
.Applying identical reasoning to the triangles with bases  and
and  , we get
, we get  so that
so that  and
and  . Substituting from this equation into the previous one gives
. Substituting from this equation into the previous one gives  , from which we get
, from which we get  and so the area of
and so the area of  is
is  .This problem can be done using mass points. Assign B a weight of 1 and realize that many of the triangles have the same altitude. After continuously using the formulas that state (The sum of the two weights) = (The middle weight), and (The weight
.This problem can be done using mass points. Assign B a weight of 1 and realize that many of the triangles have the same altitude. After continuously using the formulas that state (The sum of the two weights) = (The middle weight), and (The weight  side) = (Other weight)
side) = (Other weight)  (The other side), the problem yields the answer
(The other side), the problem yields the answer  Let the interior point be
Let the interior point be  and let the points on
and let the points on  ,
,  and
and  be
be  ,
,  and
and  , respectively. Also, let
, respectively. Also, let ![$[APE]=x,[CPD]=y.$](https://latex.artofproblemsolving.com/a/d/a/adaacb718fe2bbe09f434e15453291f1b5f8d658.png) Then notice that by Ceva's,
Then notice that by Ceva's,  However, we can deduce
However, we can deduce  from the fact that
from the fact that ![$[AFP]$](https://latex.artofproblemsolving.com/b/6/1/b61b01bca9ca7726d085f1a3e81250b4037b7e7c.png) and
and ![$[BPF]$](https://latex.artofproblemsolving.com/8/c/c/8cc258ba4a8e9e1022d7909533dfd6180eb745cc.png) share the same height. Similarly,
share the same height. Similarly,  and
and  Plug and chug and you get
Plug and chug and you get  Then notice by the same height reasoning,
Then notice by the same height reasoning,  Clear the fractions and combine like terms to get
Clear the fractions and combine like terms to get  We know
We know  so subtraction yields
so subtraction yields  or
or  Plugging this in to our previous ratio statement yields
Plugging this in to our previous ratio statement yields  so
so  Basic addition gives us
Basic addition gives us 
- It follows from the givens that
 is a perfect fourth power,
is a perfect fourth power,  is a perfect fifth power,
is a perfect fifth power,  is a perfect square and
is a perfect square and  is a perfect cube. Thus, there exist integers
is a perfect cube. Thus, there exist integers  and
and  such that
such that  ,
,  ,
,  and
and  . So
. So  . We can factor the left-hand side of this equation as a difference of two squares,
. We can factor the left-hand side of this equation as a difference of two squares,  . 19 is a prime number and
. 19 is a prime number and  so we must have
so we must have  and
and  . Then
. Then  and so
and so  ,
,  and
and  .
. - If any of the approximations
 is less than 2 or more than 3, the error associated with that term will be larger than 1, so the largest error will be larger than 1. However, if all of the
is less than 2 or more than 3, the error associated with that term will be larger than 1, so the largest error will be larger than 1. However, if all of the  are 2 or 3, the largest error will be less than 1. So in the best case, we write 19 as a sum of 7 numbers, each of which is 2 or 3. Then there must be five 3s and two 2s. It is clear that in the best appoximation, the two 2s will be used to approximate the two smallest of the
are 2 or 3, the largest error will be less than 1. So in the best case, we write 19 as a sum of 7 numbers, each of which is 2 or 3. Then there must be five 3s and two 2s. It is clear that in the best appoximation, the two 2s will be used to approximate the two smallest of the  , so our approximations are
, so our approximations are  and
and  and the largest error is
and the largest error is  , so the answer is
, so the answer is  .
. ![[asy] size(200); pointpen = black; pathpen = black + linewidth(0.8); real r = 8/15^0.5, a = 57.91, b = 93.135; pair O = (0,0), A = r*expi(pi/3); D(CR(O,r)); D(O--rotate(a/2)*A--rotate(-a/2)*A--cycle); D(O--rotate(b/2)*A--rotate(-b/2)*A--cycle); D(O--rotate((a+b)/2)*A--rotate(-(a+b)/2)*A--cycle); MP("2",(rotate(a/2)*A+rotate(-a/2)*A)/2,NE); MP("3",(rotate(b/2)*A+rotate(-b/2)*A)/2,NE); MP("4",(rotate((a+b)/2)*A+rotate(-(a+b)/2)*A)/2,NE); D(anglemark(rotate(-(a+b)/2)*A,O,rotate((a+b)/2)*A,5)); label("(alpha+beta)",(0.08,0.08),NE,fontsize(8)); [/asy]](https://latex.artofproblemsolving.com/c/c/c/ccc44394730c0756402714001ccba571e69a1bf7.png) All chords of a given length in a given circle subtend the same arc and therefore the same central angle. Thus, by the given, we can re-arrange our chords into a triangle with the circle as its circumcircle.
All chords of a given length in a given circle subtend the same arc and therefore the same central angle. Thus, by the given, we can re-arrange our chords into a triangle with the circle as its circumcircle.![[asy] size(200); pointpen = black; pathpen = black + linewidth(0.8); real r = 8/15^0.5, a = 57.91, b = 93.135; pair O = (0,0), A = r*expi(pi/3), A1 = rotate(a/2)*A, A2 = rotate(-a/2)*A, A3 = rotate(-a/2-b)*A; D(CR(O,r)); D(O--A1--A2--cycle); D(O--A2--A3--cycle); D(O--A1--A3--cycle); MP("2",(A1+A2)/2,NE); MP("3",(A2+A3)/2,E); MP("4",(A1+A3)/2,E); D(anglemark(A2,O,A1,5)); D(anglemark(A3,O,A2,5)); label("(alpha)",(0.07,0.16),NE,fontsize(8)); label("(beta)",(0.12,-0.16),NE,fontsize(8)); [/asy]](https://latex.artofproblemsolving.com/0/6/1/0618ad736b55ffe052dd977aed3aa0c72dca89d9.png) This triangle has semiperimeter
This triangle has semiperimeter  so by Heron's formula it has area
so by Heron's formula it has area  . The area of a given triangle with sides of length
. The area of a given triangle with sides of length  and circumradius of length
and circumradius of length  is also given by the formula
is also given by the formula  , so
, so  and
and  .Now, consider the triangle formed by two radii and the chord of length 2. This isosceles triangle has vertex angle
.Now, consider the triangle formed by two radii and the chord of length 2. This isosceles triangle has vertex angle  , so by the Law of Cosines,
, so by the Law of Cosines,![[2^2 = R^2 + R^2 - 2R^2cos alpha Longrightarrow cos alpha = frac{2R^2 - 4}{2R^2} = frac{17}{32}]](https://latex.artofproblemsolving.com/1/0/f/10fa5c3d8e64fbdaf60209d497940a5bba7fe5c3.png) and the answer is
and the answer is  .
.![[asy] size(200); pointpen = black; pathpen = black + linewidth(0.8); real r = 8/15^0.5, a = 57.91, b = 93.135; pair O = (0,0), A = r*expi(pi/3), A1 = rotate(a/2)*A, A2 = rotate(-a/2)*A, A3 = rotate(-a/2-b)*A; D(CR(O,r)); D(O--A1--A2--cycle); D(O--A2--A3--cycle); D(O--A1--A3--cycle); MP("2",(A1+A2)/2,NE); MP("3",(A2+A3)/2,E); MP("4",(A1+A3)/2,E); D(anglemark(A2,O,A1,5)); D(anglemark(A3,O,A2,5)); D(anglemark(A2,A3,A1,18)); label("(alpha)",(0.07,0.16),NE,fontsize(8)); label("(beta)",(0.12,-0.16),NE,fontsize(8)); label("(alpha)/2",(0.82,-1.25),NE,fontsize(8)); [/asy]](https://latex.artofproblemsolving.com/4/4/8/448c27a4bb9a18d7576a79968b61141e098c460b.png) It’s easy to see in triangle which lengths 2, 3, and 4, that the angle opposite the side 2 is
It’s easy to see in triangle which lengths 2, 3, and 4, that the angle opposite the side 2 is  , and using the Law of Cosines, we get:
, and using the Law of Cosines, we get:![[2^2 = 3^2 + 4^2 - 2cdot3cdot4cosfrac{alpha}{2}]](https://latex.artofproblemsolving.com/2/3/3/233aebba0662e3728f7166863908af375636495b.png) Which, rearranges to:
Which, rearranges to:![[21 = 24cosfrac{alpha}{2}]](https://latex.artofproblemsolving.com/c/8/3/c8347a23f80f954db15590485dc7587d3b34ecfb.png) And, that gets us:
And, that gets us:![[cosfrac{alpha}{2} = 7/8]](https://latex.artofproblemsolving.com/c/8/8/c889118bf07fb02200f73912aa1803bbe845f4d1.png) Using
Using  , we get that:
, we get that:![[cosalpha = 17/32]](https://latex.artofproblemsolving.com/2/e/0/2e051c3afff97a061a21b13d87307aeae32a56cb.png) Which gives an answer of
Which gives an answer of 
- We will be able to reach the same number of integers while
 ranges from 0 to 1 as we will when
ranges from 0 to 1 as we will when  ranges from
ranges from  to
to  for any integer
for any integer  (Quick proof:
(Quick proof:  ). Since
). Since  , the answer must be exactly 50 times the number of integers we will be able to reach as
, the answer must be exactly 50 times the number of integers we will be able to reach as  ranges from 0 to 1, including 1 but excluding 0.
ranges from 0 to 1, including 1 but excluding 0. - An ellipse is defined to be the locus of points
 such that the sum of the distances between
such that the sum of the distances between  and the two foci is constant. Let
and the two foci is constant. Let  ,
,  and
and  be the point of tangency of the ellipse with the
be the point of tangency of the ellipse with the  -axis. Then
-axis. Then  must be the point on the axis such that the sum
must be the point on the axis such that the sum  is minimal. (The last claim begs justification: Let
is minimal. (The last claim begs justification: Let  be the reflection of
be the reflection of  across the
across the  -axis. Let
-axis. Let  be where the line through
be where the line through  and
and  intersects the ellipse. We will show that
intersects the ellipse. We will show that  . Note that
. Note that  since
since  is on the
is on the  -axis. Also, since the entire ellipse is on or above the
-axis. Also, since the entire ellipse is on or above the  -axis and the line through
-axis and the line through  and
and  is perpendicular to the
is perpendicular to the  -axis, we must have
-axis, we must have  with equality if and only if
with equality if and only if  is on the
is on the  -axis. Now, we have
-axis. Now, we have![[F_1 X + F'_2 X = F_1 X + F_2 X = F_1 Y + F_2 Y leq F_1 Y + F’_2 Y]](https://latex.artofproblemsolving.com/c/6/6/c6614c11882a08934b8102073f99e47eacb236c0.png) But the right most sum is the straight-line distance from
But the right most sum is the straight-line distance from  to
to  and the left is the distance of some path from
and the left is the distance of some path from  to
to  ., so this is only possible if we have equality and thus
., so this is only possible if we have equality and thus  ). Finding the optimal location for
). Finding the optimal location for  is a classic problem: for any path from
is a classic problem: for any path from  to
to  and then back to
and then back to  , we can reflect (as above) the second leg of this path (from
, we can reflect (as above) the second leg of this path (from  to
to  ) across the
) across the  -axis. Then our path connects
-axis. Then our path connects  to the reflection
to the reflection  of
of  via some point on the
via some point on the  -axis, and this path will have shortest length exactly when our original path has shortest length. This occurs exactly when we have a straight-line path, and by the above argument, this path passes through the point of tangency of the ellipse with the
-axis, and this path will have shortest length exactly when our original path has shortest length. This occurs exactly when we have a straight-line path, and by the above argument, this path passes through the point of tangency of the ellipse with the  axis.
axis.![[asy] size(200); pointpen=black;pathpen=black+linewidth(0.6);pen f = fontsize(10); pair F1=(9,20),F2=(49,55); D(shift((F1+F2)/2)*rotate(41.186)*scale(85/2,10*11^.5)*unitcircle); D((-20,0)--(80,0)--(0,0)--(0,80)--(0,-60)); path p = F1--(49,-55); pair X = IP(p,(0,0)--(80,0)); D(p,dashed);D(F1--X--F2);D(F1);D(F2);D((49,-55)); MP("X",X,SW,f); MP("F_1",F1,NW,f); MP("F_2",F2,NW,f); MP("F_2'",(49,-55),NE,f); [/asy]](https://latex.artofproblemsolving.com/e/1/7/e17edad4abef8ffedba4e8086dacea0dc6c8c309.png) The sum of the two distances
The sum of the two distances  and
and  is therefore equal to the length of the segment
is therefore equal to the length of the segment  , which by the distance formula is just
, which by the distance formula is just  .Finally, let
.Finally, let  and
and  be the two endpoints of the major axis of the ellipse. Then by symmetry
be the two endpoints of the major axis of the ellipse. Then by symmetry  so
so  (because
(because  is on the ellipse), so the answer is
is on the ellipse), so the answer is  .
. - Let
 denote the probability that the bug is at
denote the probability that the bug is at  after it has crawled
after it has crawled  meters. Since the bug can only be at vertex
meters. Since the bug can only be at vertex  if it just left a vertex which is not
if it just left a vertex which is not  , we have
, we have  . We also know
. We also know  , so we can quickly compute
, so we can quickly compute  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  , so the answer is
, so the answer is  . One can solve this recursion fairly easily to determine a closed-form expression for
. One can solve this recursion fairly easily to determine a closed-form expression for  .
. - If
 denotes the greatest common divisor of
denotes the greatest common divisor of  and
and  , then we have
, then we have  . Now assuming that
. Now assuming that  divides
divides  , it must divide
, it must divide  if it is going to divide the entire expression
if it is going to divide the entire expression  .Thus the equation turns into
.Thus the equation turns into  . Now note that since
. Now note that since  is odd for integral
is odd for integral  , we can multiply the left integer,
, we can multiply the left integer,  , by a power of two without affecting the greatest common divisor. Since the
, by a power of two without affecting the greatest common divisor. Since the  term is quite restrictive, let's multiply by
term is quite restrictive, let's multiply by  so that we can get a
so that we can get a  in there.So
in there.So  . It simplified the way we wanted it to! Now using similar techniques we can write
. It simplified the way we wanted it to! Now using similar techniques we can write  . Thus
. Thus  must divide
must divide  for every single
for every single  . This means the largest possible value for
. This means the largest possible value for  is
is  , and we see that it can be achieved when
, and we see that it can be achieved when  .We know that
.We know that  and
and  . Since we want to find the GCD of
. Since we want to find the GCD of  and
and  , we can use the Euclidean algorithm:
, we can use the Euclidean algorithm: Now, the question is to find the GCD of
Now, the question is to find the GCD of  and
and  . We subtract
. We subtract  100 times from
100 times from  . This leaves us with
. This leaves us with  . We want this to equal 0, so solving for
. We want this to equal 0, so solving for  gives us
gives us  . The last remainder is 0, thus
. The last remainder is 0, thus  is our GCD.
is our GCD.
If Solution 2 is not entirely obvious, our answer is the max possible range of . Using the Euclidean Algorithm on
. Using the Euclidean Algorithm on  and
and  yields that they are relatively prime. Thus, the only way the GCD will not be 1 is if the
yields that they are relatively prime. Thus, the only way the GCD will not be 1 is if the term share factors with the
term share factors with the  . Using the Euclidean Algorithm,
. Using the Euclidean Algorithm,  . Thus, the max GCD is 401.
. Thus, the max GCD is 401.
We can just plug in Euclidean algorithm, to go from to
to  to
to  to get
to get  . Now we know that no matter what,
. Now we know that no matter what,  is relatively prime to
is relatively prime to  . Therefore the equation can be simplified to:
. Therefore the equation can be simplified to:  . Subtracting
. Subtracting  from
from  results in
results in  . The greatest possible value of this is
. The greatest possible value of this is  , an happens when
, an happens when  .
. - Let us suppose for convenience that there were
 players overall. Among the
players overall. Among the  players not in the weakest 10 there were
players not in the weakest 10 there were  games played and thus
games played and thus  points earned. By the givens, this means that these
points earned. By the givens, this means that these  players also earned
players also earned  points against our weakest 10. Now, the 10 weakest players playing amongst themselves played
points against our weakest 10. Now, the 10 weakest players playing amongst themselves played  games and so earned 45 points playing each other. Then they also earned 45 points playing against the stronger
games and so earned 45 points playing each other. Then they also earned 45 points playing against the stronger  players. Since every point earned falls into one of these categories, It follows that the total number of points earned was
players. Since every point earned falls into one of these categories, It follows that the total number of points earned was  . However, there was one point earned per game, and there were a total of
. However, there was one point earned per game, and there were a total of  games played and thus
games played and thus  points earned. So we have
points earned. So we have  so
so  and
and  and
and  or
or  . Now, note that the top
. Now, note that the top  players got
players got  points in total (by our previous calculation) for an average of
points in total (by our previous calculation) for an average of  , while the bottom 10 got 90 points total, for an average of 9. Thus we must have
, while the bottom 10 got 90 points total, for an average of 9. Thus we must have  , so
, so  and the answer is
and the answer is  .Suppose that there are
.Suppose that there are  players participating in the tournament. We break this up into a group of the weakest ten, and the other
players participating in the tournament. We break this up into a group of the weakest ten, and the other  people. Note that the
people. Note that the  players who played each other generated a total of
players who played each other generated a total of  points playing each other. Thus, they earned
points playing each other. Thus, they earned  playing the
playing the  other people. Thus, the
other people. Thus, the  people earned a total of
people earned a total of  points playing vs. this group of 10 people, and also earned a total of
points playing vs. this group of 10 people, and also earned a total of  playing against themselves. Since each match gives a total of one point, we must have that
playing against themselves. Since each match gives a total of one point, we must have that  . Expanding and simplifying gives us
. Expanding and simplifying gives us  . Thus,
. Thus,  or
or  . Note however that if
. Note however that if  , then the strongest
, then the strongest  people get a total of
people get a total of  playing against the weakest
playing against the weakest  who gained
who gained  points vs them, which is a contradiction since it must be larger. Thus,
points vs them, which is a contradiction since it must be larger. Thus,  .Solution by GameMaster402
.Solution by GameMaster402 - Note that gluing two of the given polyhedra together along a hexagonal face (rotated
 from each other) yields a cube, so the volume is
from each other) yields a cube, so the volume is  .Image:
.Image: 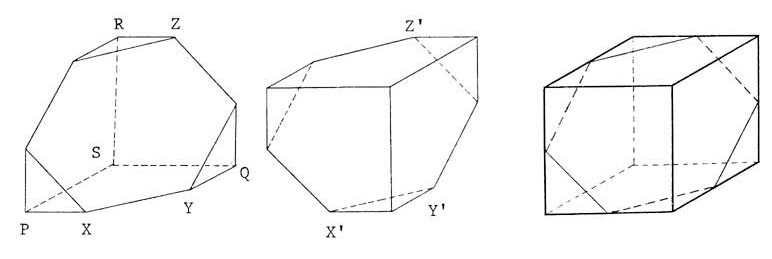
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









