- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1986AIME 真题及答案解析
1986AIME 真题及答案解析
Problem 1
What is the sum of the solutions to the equation ![]() ?
?
Problem 2
Evaluate the product ![]() .
.
Problem 3
If ![]() and
and ![]() , what is
, what is ![]() ?
?
Problem 4
Determine ![]() if
if ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() satisfy the system of equations below.
satisfy the system of equations below.
Problem 5
What is that largest positive integer ![]() for which
for which ![]() is divisible by
is divisible by ![]() ?
?
Problem 6
The pages of a book are numbered ![]() through
through ![]() . When the page numbers of the book were added, one of the page numbers was mistakenly added twice, resulting in an incorrect sum of
. When the page numbers of the book were added, one of the page numbers was mistakenly added twice, resulting in an incorrect sum of ![]() . What was the number of the page that was added twice?
. What was the number of the page that was added twice?
Problem 7
The increasing sequence ![]() consists of all those positive integers which are powers of 3 or sums of distinct powers of 3. Find the
consists of all those positive integers which are powers of 3 or sums of distinct powers of 3. Find the ![]() term of this sequence.
term of this sequence.
Problem 8
Let ![]() be the sum of the base
be the sum of the base ![]() logarithms of all the proper divisors of
logarithms of all the proper divisors of ![]() . What is the integer nearest to
. What is the integer nearest to ![]() ?
?
Problem 9
In ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . An interior point
. An interior point ![]() is then drawn, and segments are drawn through
is then drawn, and segments are drawn through ![]() parallel to the sides of the triangle. If these three segments are of an equal length
parallel to the sides of the triangle. If these three segments are of an equal length ![]() , find
, find ![]() .
.
Problem 10
In a parlor game, the magician asks one of the participants to think of a three digit number ![]() where
where ![]() ,
, ![]() , and
, and ![]() represent digits in base
represent digits in base ![]() in the order indicated. The magician then asks this person to form the numbers
in the order indicated. The magician then asks this person to form the numbers ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , to add these five numbers, and to reveal their sum,
, to add these five numbers, and to reveal their sum, ![]() . If told the value of
. If told the value of ![]() , the magician can identify the original number,
, the magician can identify the original number, ![]() . Play the role of the magician and determine the
. Play the role of the magician and determine the ![]() if
if ![]() .
.
Problem 11
The polynomial ![]() may be written in the form
may be written in the form ![]() , where
, where ![]() and the
and the ![]() 's are constants. Find the value of
's are constants. Find the value of ![]() .
.
Problem 12
Let the sum of a set of numbers be the sum of its elements. Let ![]() be a set of positive integers, none greater than 15. Suppose no two disjoint subsets of
be a set of positive integers, none greater than 15. Suppose no two disjoint subsets of ![]() have the same sum. What is the largest sum a set
have the same sum. What is the largest sum a set ![]() with these properties can have?
with these properties can have?
Problem 13
In a sequence of coin tosses, one can keep a record of instances in which a tail is immediately followed by a head, a head is immediately followed by a head, and etc. We denote these by TH, HH, and etc. For example, in the sequence TTTHHTHTTTHHTTH of 15 coin tosses we observe that there are two HH, three HT, four TH, and five TT subsequences. How many different sequences of 15 coin tosses will contain exactly two HH, three HT, four TH, and five TT subsequences?
Problem 14
The shortest distances between an interior diagonal of a rectangular parallelepiped, ![]() , and the edges it does not meet are
, and the edges it does not meet are ![]() ,
, ![]() , and
, and ![]() . Determine the volume of
. Determine the volume of ![]() .
.
Problem 15
Let triangle ![]() be a right triangle in the
be a right triangle in the ![]() -plane with a right angle at
-plane with a right angle at ![]() . Given that the length of the hypotenuse
. Given that the length of the hypotenuse ![]() is
is ![]() , and that the medians through
, and that the medians through ![]() and
and ![]() lie along the lines
lie along the lines ![]() and
and ![]() respectively, find the area of triangle
respectively, find the area of triangle ![]() .
.
1986AIME 详细解析
- Let
![$y = sqrt[4]{x}$](https://latex.artofproblemsolving.com/f/5/8/f5838ae6bb955f1f7afe1c28d870b6cd091b78ac.png) . Then we have
. Then we have  , or, by simplifying,
, or, by simplifying,![[y^2 - 7y + 12 = (y - 3)(y - 4) = 0.]](https://latex.artofproblemsolving.com/f/2/1/f2177dfb0ca3080c826bfa7e508ae0dcd37ef80e.png) This means that
This means that ![$sqrt[4]{x} = y = 3$](https://latex.artofproblemsolving.com/7/2/3/723fc9924d37616a4675a26e831751451b6904d6.png) or
or  .Thus the sum of the possible solutions for
.Thus the sum of the possible solutions for  is
is  .
. - Simplify by repeated application of the difference of squares.
- Since
 is the reciprocal function of
is the reciprocal function of  :
: Thus,
Thus,  Using the tangent addition formula:
Using the tangent addition formula: .
. - Adding all five equations gives us
 so
so  . Subtracting this from the fourth given equation gives
. Subtracting this from the fourth given equation gives  and subtracting it from the fifth given equation gives
and subtracting it from the fifth given equation gives  , so our answer is
, so our answer is  .
. - If
 ,
,  . Using the Euclidean algorithm, we have
. Using the Euclidean algorithm, we have 

 , so
, so  must divide
must divide  . The greatest integer
. The greatest integer  for which
for which  divides
divides  is
is  ; we can double-check manually and we find that indeed
; we can double-check manually and we find that indeed  .In a similar manner, we can apply synthetic division. We are looking for
.In a similar manner, we can apply synthetic division. We are looking for  . Again,
. Again,  must be a factor of
must be a factor of  .The key to this problem is to realize that
.The key to this problem is to realize that  for all
for all  . Since we are asked to find the maximum possible
. Since we are asked to find the maximum possible  such that
such that  , we have:
, we have:  . This is because of the property that states that if
. This is because of the property that states that if  and
and  , then
, then  . Since, the largest factor of 900 is itself we have:
. Since, the largest factor of 900 is itself we have: 
- Denote the page number as
 , with
, with  . The sum formula shows that
. The sum formula shows that  . Since
. Since  cannot be very large, disregard it for now and solve
cannot be very large, disregard it for now and solve  . The positive root for
. The positive root for  . Quickly testing, we find that
. Quickly testing, we find that  is too large, but if we plug in
is too large, but if we plug in  we find that our answer is
we find that our answer is  .
. - Rewrite all of the terms in base 3. Since the numbers are sums of distinct powers of 3, in base 3 each number is a sequence of 1s and 0s (if there is a 2, then it is no longer the sum of distinct powers of 3). Therefore, we can recast this into base 2 (binary) in order to determine the 100th number.
 is equal to
is equal to  , so in binary form we get
, so in binary form we get  . However, we must change it back to base 10 for the answer, which is
. However, we must change it back to base 10 for the answer, which is  .Notice that the first term of the sequence is
.Notice that the first term of the sequence is  , the second is
, the second is  , the fourth is
, the fourth is  , and so on. Thus the
, and so on. Thus the  term of the sequence is
term of the sequence is  . Now out of
. Now out of  terms which are of the form
terms which are of the form  +
+  ,
,  of them include
of them include  and
and  do not. The smallest term that includes
do not. The smallest term that includes  , i.e.
, i.e.  , is greater than the largest term which does not, or
, is greater than the largest term which does not, or  . So the
. So the  th term will be
th term will be  , then
, then  , then
, then  , then
, then  , and finally
, and finally  After the
After the  th power of 3 in the sequence, the number of terms after that power but before the
th power of 3 in the sequence, the number of terms after that power but before the  th power of 3 is equal to the number of terms before the
th power of 3 is equal to the number of terms before the  th power, because those terms after the
th power, because those terms after the  th power are just the
th power are just the  th power plus all the distinct combinations of powers of 3 before it, which is just all the terms before it. Adding the powers of
th power plus all the distinct combinations of powers of 3 before it, which is just all the terms before it. Adding the powers of  and the terms that come after them, we see that the
and the terms that come after them, we see that the  th term is after
th term is after  , which is the
, which is the  th term. Also, note that the
th term. Also, note that the  th term after the
th term after the  th power of 3 is equal to the power plus the
th power of 3 is equal to the power plus the  th term in the entire sequence. Thus, the
th term in the entire sequence. Thus, the  th term is
th term is  plus the
plus the  th term. Using the same logic, the
th term. Using the same logic, the  th term is
th term is  plus the
plus the  th term,
th term,  . We now have
. We now have 
- The prime factorization of
 , so there are
, so there are  divisors, of which
divisors, of which  are proper. The sum of multiple logarithms of the same base is equal to the logarithm of the products of the numbers.Writing out the first few terms, we see that the answer is equal to
are proper. The sum of multiple logarithms of the same base is equal to the logarithm of the products of the numbers.Writing out the first few terms, we see that the answer is equal to![[log 1 + log 2 + log 4 + ldots + log 1000000 = log (2^05^0)(2^15^0)(2^25^0)cdots (2^65^6).]](https://latex.artofproblemsolving.com/8/5/4/854ec44c63903fd31f1c66109b580c04366c9661.png) Each power of
Each power of  appears
appears  times; and the same goes for
times; and the same goes for  . So the overall power of
. So the overall power of  and
and  is
is  . However, since the question asks for proper divisors, we exclude
. However, since the question asks for proper divisors, we exclude  , so each power is actually
, so each power is actually  times. The answer is thus
times. The answer is thus  .Since the prime factorization of
.Since the prime factorization of  is
is  , the number of factors in
, the number of factors in  is
is  . You can pair them up into groups of two so each group multiplies to
. You can pair them up into groups of two so each group multiplies to  . Note that
. Note that  . Thus, the sum of the logs of the divisors is half the number of divisors of
. Thus, the sum of the logs of the divisors is half the number of divisors of  (since they are asking only for proper divisors), and the answer is
(since they are asking only for proper divisors), and the answer is  .
. ![[asy] size(200); pathpen = black; pointpen = black +linewidth(0.6); pen s = fontsize(10); pair C=(0,0),A=(510,0),B=IP(circle(C,450),circle(A,425)); /* construct remaining points */ pair Da=IP(Circle(A,289),A--B),E=IP(Circle(C,324),B--C),Ea=IP(Circle(B,270),B--C); pair D=IP(Ea--(Ea+A-C),A--B),F=IP(Da--(Da+C-B),A--C),Fa=IP(E--(E+A-B),A--C); D(MP("A",A,s)--MP("B",B,N,s)--MP("C",C,s)--cycle); dot(MP("D",D,NE,s));dot(MP("E",E,NW,s));dot(MP("F",F,s));dot(MP("D'",Da,NE,s));dot(MP("E'",Ea,NW,s));dot(MP("F'",Fa,s)); D(D--Ea);D(Da--F);D(Fa--E); MP("450",(B+C)/2,NW);MP("425",(A+B)/2,NE);MP("510",(A+C)/2); /*P copied from above solution*/ pair P = IP(D--Ea,E--Fa); dot(MP("P",P,N)); [/asy]](https://latex.artofproblemsolving.com/8/e/1/8e19916c4ed37209e832673ba0274846bb4c4246.png)
 as shown above. As a result of the lines being parallel, all three smaller triangles and the larger triangle are similar (
as shown above. As a result of the lines being parallel, all three smaller triangles and the larger triangle are similar ( ). The remaining three sections are parallelograms.By similar triangles,
). The remaining three sections are parallelograms.By similar triangles,  and
and  . Since
. Since  , we have
, we have  , so
, so  .
.- Let
 be the number
be the number  . Observe that
. Observe that  so
so![[mequiv -3194equiv -86equiv 136pmod{222}]](https://latex.artofproblemsolving.com/9/7/2/97290b737bbe1f40c3f47cef903ca8eacfa1f153.png) This reduces
This reduces  to one of
to one of  . But also
. But also  so
so  . Of the four options, only
. Of the four options, only  satisfies this inequality.
satisfies this inequality. - Using the geometric series formula,
 . Since
. Since  , this becomes
, this becomes  . We want
. We want  , which is the coefficient of the
, which is the coefficient of the  term in
term in  (because the
(because the  in the denominator reduces the degrees in the numerator by
in the denominator reduces the degrees in the numerator by  ). By the Binomial Theorem, this is
). By the Binomial Theorem, this is  .Again, notice
.Again, notice  . So
. So We want the coefficient of the
We want the coefficient of the  term of each power of each binomial, which by the binomial theorem is
term of each power of each binomial, which by the binomial theorem is  . The Hockey Stick Identity tells us that this quantity is equal to
. The Hockey Stick Identity tells us that this quantity is equal to  .
. - By using the greedy algorithm, we obtain
 , with
, with  . We must now prove that no such set has sum greater than 61. Suppose such a set
. We must now prove that no such set has sum greater than 61. Suppose such a set  existed. Then
existed. Then  must have more than 4 elements, otherwise its sum would be at most
must have more than 4 elements, otherwise its sum would be at most  .
. can't have more than 5 elements. To see why, note that at least
can't have more than 5 elements. To see why, note that at least  of its subsets have at most four elements (the number of subsets with no elements plus the number of subsets with one element and so on), and each of them have sum at most 54. By the Pigeonhole Principle, two of these subsets would have the same sum.Thus,
of its subsets have at most four elements (the number of subsets with no elements plus the number of subsets with one element and so on), and each of them have sum at most 54. By the Pigeonhole Principle, two of these subsets would have the same sum.Thus,  would have to have 5 elements.
would have to have 5 elements.  contains both 15 and 14 (otherwise its sum is at most
contains both 15 and 14 (otherwise its sum is at most  ). It follows that
). It follows that  cannot contain both
cannot contain both  and
and  for any
for any  , or the subsets
, or the subsets  and
and  would have the same sum. So now
would have the same sum. So now  must contain 13 (otherwise its sum is at most
must contain 13 (otherwise its sum is at most  ), and
), and  cannot contain 12, or the subsets
cannot contain 12, or the subsets  and
and  would have the same sum.Now the only way
would have the same sum.Now the only way  could have sum at least
could have sum at least  would be if
would be if  . But the subsets
. But the subsets  and
and  have the same sum, so this set does not work. Therefore no
have the same sum, so this set does not work. Therefore no  with sum greater than 61 is possible and 61 is indeed the maximum.
with sum greater than 61 is possible and 61 is indeed the maximum. - Let's consider each of the sequences of two coin tosses as an operation instead; this operation takes a string and adds the next coin toss on (eg, THHTH + HT = THHTHT). We examine what happens to the last coin toss. Adding HH or TT is simply an identity for the last coin toss, so we will ignore them for now. However, adding HT or TH switches the last coin. H switches to T three times, but T switches to H four times; hence it follows that our string will have a structure of THTHTHTH.Now we have to count all of the different ways we can add the identities back in. There are 5 TT subsequences, which means that we have to add 5 T into the strings, as long as the new Ts are adjacent to existing Ts. There are already 4 Ts in the sequence, and since order doesn’t matter between different tail flips this just becomes the ball-and-urn argument. We want to add 5 balls into 4 urns, which is the same as 3 dividers; hence this gives
 combinations. We do the same with 2 Hs to get
combinations. We do the same with 2 Hs to get  combinations; thus there are
combinations; thus there are  possible sequences.SLIGHT VARIATION ON FINAL ARGUMENTThe structure of the final order is T_H_T_H_T_H_T_H_, and there are 4 spots to put the 2 heads in, and 4 spots to put the 5 tails in. By using the formula for distributing r identical objects into n distinct boxes
possible sequences.SLIGHT VARIATION ON FINAL ARGUMENTThe structure of the final order is T_H_T_H_T_H_T_H_, and there are 4 spots to put the 2 heads in, and 4 spots to put the 5 tails in. By using the formula for distributing r identical objects into n distinct boxes  and multiplication, the answer is
and multiplication, the answer is  *
*  =560
=560 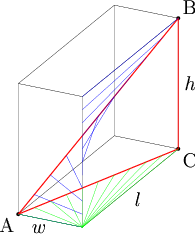
 . All the blue lines are perpendicular lines to
. All the blue lines are perpendicular lines to  and their other points are on
and their other points are on  , the main diagonal. The green lines are projections of the blue lines onto the bottom face; all of the green lines originate in the corner and reach out to
, the main diagonal. The green lines are projections of the blue lines onto the bottom face; all of the green lines originate in the corner and reach out to  , and have the same lengths as their corresponding blue lines. So we want to find the shortest distance between
, and have the same lengths as their corresponding blue lines. So we want to find the shortest distance between  and that corner, which is
and that corner, which is  .So we have:
.So we have:![[frac {lw}{sqrt {l^2 + w^2}} = frac {10}{sqrt {5}}]](https://latex.artofproblemsolving.com/0/b/e/0bebea7d48fd0a5003ac28d8f9ca77d4e9440192.png)
![[frac {hw}{sqrt {h^2 + w^2}} = frac {30}{sqrt {13}}]](https://latex.artofproblemsolving.com/2/7/b/27bfdb3306a3193e87d8eecc8b6325a312d3b778.png)
![[frac {hl}{sqrt {h^2 + l^2}} = frac {15}{sqrt {10}}]](https://latex.artofproblemsolving.com/a/c/5/ac5a6c874fcfdd4b9d890e61e3893c6900954eba.png) Notice the familiar roots:
Notice the familiar roots:  ,
,  ,
,  , which are
, which are  ,
,  ,
,  , respectively. (This would give us the guess that the sides are of the ratio 1:2:3, but let's provide the complete solution.)
, respectively. (This would give us the guess that the sides are of the ratio 1:2:3, but let's provide the complete solution.)![[frac {l^2w^2}{l^2 + w^2} = frac {1}{frac {1}{l^2} + frac {1}{w^2}} = 20]](https://latex.artofproblemsolving.com/3/e/9/3e9936cd4e1fcda5d6227228ea37f82bc132500a.png)
![[frac {h^2w^2}{h^2 + w^2} = frac {1}{frac {1}{h^2} + frac {1}{w^2}} = frac {900}{13}]](https://latex.artofproblemsolving.com/9/0/8/908a897173a9680da4f715f78e3264c7d28cc179.png)
![[frac {h^2l^2}{h^2 + l^2} = frac {1}{frac {1}{h^2} + frac {1}{l^2}} = frac {45}{2}]](https://latex.artofproblemsolving.com/9/a/e/9aef0d812e00178d2eaf470ffcc955c630ea9730.png) We invert the above equations to get a system of linear equations in
We invert the above equations to get a system of linear equations in  ,
,  , and
, and  :
:![[frac {1}{l^2} + frac {1}{w^2} = frac {45}{900}]](https://latex.artofproblemsolving.com/0/5/f/05f902c1b2ad93ed0fa5bcacb3b18ca1c87adddb.png)
![[frac {1}{h^2} + frac {1}{w^2} = frac {13}{900}]](https://latex.artofproblemsolving.com/0/b/1/0b1ea7acfaa5f3ffa877563a5b960322779d8e49.png)
![[frac {1}{h^2} + frac {1}{l^2} = frac {40}{900}]](https://latex.artofproblemsolving.com/d/9/3/d9348c7885416f54202794f370267f1d50d01eb9.png)
We see that
 ,
,  ,
,  . Therefore
. Therefore  .
.- Translate so the medians are
 , and
, and  , then model the points
, then model the points  and
and  .
.  is the centroid, and is the average of the vertices, so
is the centroid, and is the average of the vertices, so 
 so
so


 and
and  are perpendicular, so the product of their slopes is
are perpendicular, so the product of their slopes is  , giving
, giving

Combining
 and
and  , we get
, we get 
Using the determinant product for area of a triangle (this simplifies nicely, add columns 1 and 2, add rows 2 and 3), the area is
 , so we get the answer to be
, so we get the answer to be  .
.
学术活动报名扫码了解!免费领取历年真题!

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








