Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

1987AIME 真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月12日上午11:50

1987AIME 真题及答案解析

答案解析请参考文末

Problem 1

An ordered pair $(m,n)$ of non-negative integers is called "simple" if the addition $m+n$ in base $10$ requires no carrying. Find the number of simple ordered pairs of non-negative integers that sum to $1492$ .

Problem 2

What is the largest possible distance between two points, one on the sphere of radius 19 with center $(-2,-10,5),$ and the other on the sphere of radius 87 with center $(12,8,-16)$ ?

Problem 3

By a proper divisor of a natural number we mean a positive integral divisor other than 1 and the number itself. A natural number greater than 1 will be called "nice" if it is equal to the product of its distinct proper divisors. What is the sum of the first ten nice numbers?

Problem 4

Find the area of the region enclosed by the graph of $|x-60|+|y|=left|frac{x}{4}right|.$

Problem 5

Find $3x^2 y^2$ if $x$ and $y$ are integers such that $y^2 + 3x^2 y^2 = 30x^2 + 517$ .

Problem 6

Rectangle $ABCD$ is divided into four parts of equal area by five segments as shown in the figure, where $XY = YB + BC + CZ = ZW = WD + DA + AX$ , and $PQ$ is parallel to $AB$ . Find the length of $AB$ (in cm) if $BC = 19$ cm and $PQ = 87$ cm.

AIME 1987 Problem 6.png

Problem 7

Let $[r,s]$ denote the least common multiple of positive integers $r$ and $s$ . Find the number of ordered triples $(a,b,c)$ of positive integers for which $[a,b] = 1000$ , $[b,c] = 2000$ , and $[c,a] = 2000$ .

Problem 8

What is the largest positive integer $n$ for which there is a unique integer $k$ such that $frac{8}{15} < frac{n}{n + k} < frac{7}{13}$ ?

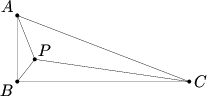
Problem 9

Triangle $ABC$ has right angle at $B$ , and contains a point $P$ for which $PA = 10$ , $PB = 6$ , and $angle APB = angle BPC = angle CPA$ . Find $PC$ .

AIME 1987 Problem 9.png

Problem 10

Al walks down to the bottom of an escalator that is moving up and he counts 150 steps. His friend, Bob, walks up to the top of the escalator and counts 75 steps. If Al's speed of walking (in steps per unit time) is three times Bob's walking speed, how many steps are visible on the escalator at a given time? (Assume that this value is constant.)

Problem 11

Find the largest possible value of $k$ for which $3^{11}$ is expressible as the sum of $k$ consecutive positive integers.

Problem 12

Let $m$ be the smallest integer whose cube root is of the form $n+r$ , where $n$ is a positive integer and $r$ is a positive real number less than $1/1000$ . Find $n$ .

Problem 13

A given sequence $r_1, r_2, dots, r_n$ of distinct real numbers can be put in ascending order by means of one or more "bubble passes". A bubble pass through a given sequence consists of comparing the second term with the first term, and exchanging them if and only if the second term is smaller, then comparing the third term with the second term and exchanging them if and only if the third term is smaller, and so on in order, through comparing the last term, $r_n$ , with its current predecessor and exchanging them if and only if the last term is smaller.

The example below shows how the sequence 1, 9, 8, 7 is transformed into the sequence 1, 8, 7, 9 by one bubble pass. The numbers compared at each step are underlined.

$underline{1 quad 9} quad 8 quad 7$ $1 quad {}underline{9 quad 8} quad 7$ $1 quad 8 quad underline{9 quad 7}$ $1 quad 8 quad 7 quad 9$ Suppose that $n = 40$ , and that the terms of the initial sequence $r_1, r_2, dots, r_{40}$ are distinct from one another and are in random order. Let $p/q$ , in lowest terms, be the probability that the number that begins as $r_{20}$ will end up, after one bubble pass, in the $30^{mbox{th}}$ place. Find $p + q$ .

Problem 14

Compute

$frac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}$ .

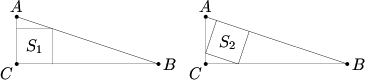
Problem 15

Squares $S_1$ and $S_2$ are inscribed in right triangle $ABC$ , as shown in the figures below. Find $AC + CB$ if area $(S_1) = 441$ and area $(S_2) = 440$ .

AIME 1987 Problem 15.png

Since no carrying over is allowed, the range of possible values of any digit of $m$ is from $0$ to the respective digit in $1492$ (the values of $n$ are then fixed). Thus, the number of ordered pairs will be $(1 + 1)(4 + 1)(9 + 1)(2 + 1) = 2cdot 5cdot 10cdot 3 = boxed{300}$ .
If you do not understand the above solution, consider this. For every positive integer $m$ , there is only one whole number $n$ that you can add to it to obtain the required sum. Also, the total number of non-negative integers that are smaller than or equal to an integer $a$ is $(a + 1)$ because there are $(a - 1)$ positive integers that are less than it, in addition to $0$ and itself.
The distance between the two centers of the spheres can be determined via the distance formula in three dimensions: $sqrt{(12 - (-2))^2 + (8 - (-10))^2 + (-16 - 5)^2} = sqrt{14^2 + 18^2 + 21^2} = 31$ . The largest possible distance would be the sum of the two radii and the distance between the two centers, making it $19 + 87 + 31 = boxed{137}$ .
Let denote the product of the distinct proper divisors of . A number is nice in one of two instances:
1. It has exactly two distinct prime divisors.
  
  If we let $n = pq$ , where $p,q$ are the prime factors, then its proper divisors are $p$ and $q$ , and $p(n) = p cdot q = n$ .
2. It is the cube of a prime number.
  
  If we let $n=p^3$ with $p$ prime, then its proper divisors are $p$ and $p^2$ , and $p(n) = p cdot p^2 =n$ .
We now show that the above are the only two cases. Suppose that another nice number existed that does not fall into one of these two categories. Then we can either express it in the form $n = pqr$ (with $p,q$ prime and $r > 1$ ) or $n = p^e$ (with $e neq 3$ ).

In the former case, it suffices to note that $p(n) ge (pr) cdot (qr) = pqr^2 > pqr = n$ .

In the latter case, then $p(n) = p cdot p^2 cdots p^{(e-1)} = p^{(e-1)e/2}$ .

For $p(n) = n$ , we need $p^{(e-1)e/2} = p^e Longrightarrow e^2 - e = 2e Longrightarrow$ $e = 0 or e = 3$ .

Since $e neq 3$ , in the case $e = 0 Longrightarrow n = 1$ does not work.

Thus, listing out the first ten numbers to fit this form, $2 cdot 3 = 6, 2^3 = 8, 2 cdot 5 = 10,$ $2 cdot 7 = 14, 3 cdot 5 = 15, 3 cdot 7 = 21,$ $2 cdot 11 = 22, 2 cdot 13 = 26,$ $3^3 = 27, 3 cdot 11 = 33$ . Summing these yields $boxed{182}$ .

Alternatively, we could note that $n$ is only nice when it only has two divisors, which, when multiplied, clearly yield $n$ . We know that when the prime factorization of $n = a_1^{b_1} cdot a_2^{b_2} cdot a_3^{b_3} . . . cdot a_m^{b_m}$ , the number of factors $f(n)$ of $n$ is $[f(n) = (b_1 + 1)(b_2 +1)(b_3 +1) . . . (b_m +1).]$

Since $n$ is nice, it may only have $4$ factors ( $1$ , $n$ , $p$ , and $q$ ). This means that $f(n) = 4$ . The number $4$ can only be factored into $(2)(2)$ or $(4)(1)$ , which means that either $b_1 = 1$ and $b_2 = 1$ , or $b_1 = 3$ . Therefore the only two cases are $n = pq$ , or $n = p^3$ .
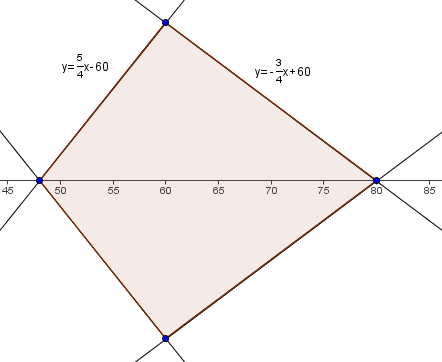Since is nonnegative, . Solving this gives us two equations: . Thus, . The maximum and minimum y value is when , which is when and . Since the graph is symmetric about the y-axis, we just need casework upon . , so we break up the condition :
- $x - 60 > 0$ . Then $y = -frac{3}{4}x+60$ .
- $x - 60 < 0$ . Then $y = frac{5}{4}x-60$ .
The area of the region enclosed by the graph is that of the quadrilateral defined by the points $(48,0), (60,15), (80,0), (60,-15)$ . Breaking it up into triangles and solving or using shoelace, we get $2 cdot frac{1}{2}(80 - 48)(15) = boxed{480}$ .
If we move the $x^2$ term to the left side, it is factorable: $[(3x^2 + 1)(y^2 - 10) = 517 - 10]$ $507$ is equal to $3 cdot 13^2$ . Since $x$ and $y$ are integers, $3x^2 + 1$ cannot equal a multiple of three. $169$ doesn't work either, so $3x^2 + 1 = 13$ , and $x^2 = 4$ . This leaves $y^2 - 10 = 39$ , so $y^2 = 49$ . Thus, $3x^2 y^2 = 3 times 4 times 49 = boxed{588}$ .
Since $XY = WZ$ , $PQ = PQ$ and the areas of the trapezoids $PQZW$ and $PQYX$ are the same, then the heights of the trapezoids are the same. Thus both trapezoids have area $frac{1}{2} cdot frac{19}{2}(XY + PQ) = frac{19}{4}(XY + 87)$ . This number is also equal to one quarter the area of the entire rectangle, which is $frac{19cdot AB}{4}$ , so we have $AB = XY + 87$ .In addition, we see that the perimeter of the rectangle is $2AB + 38 = XA + AD + DW + WZ + ZC + CB + BY + YX = 4XY$ , so $AB + 19 = 2XY$ .Solving these two equations gives $AB = boxed{193}$ .
It's clear that we must have $a = 2^j5^k$ , $b = 2^m 5^n$ and $c = 2^p5^q$ for some nonnegative integers $j, k, m, n, p, q$ . Dealing first with the powers of 2: from the given conditions, $max(j, m) = 3$ , $max(m, p) = max(p, j) = 4$ . Thus we must have $p = 4$ and at least one of $m, j$ equal to 3. This gives 7 possible triples $(j, m, p)$ : $(0, 3, 4), (1, 3, 4), (2, 3, 4), (3, 3, 4), (3, 2, 4), (3, 1, 4)$ and $(3, 0, 4)$ .Now, for the powers of 5: we have $max(k, n) = max(n, q) = max(q, k) = 3$ . Thus, at least two of $k, n, q$ must be equal to 3, and the other can take any value between 0 and 3. This gives us a total of 10 possible triples: $(3, 3, 3)$ and three possibilities of each of the forms $(3, 3, n)$ , $(3, n, 3)$ and $(n, 3, 3)$ .Since the exponents of 2 and 5 must satisfy these conditions independently, we have a total of $7 cdot 10 = 70$ possible valid triples. $1000 = 2^35^3$ and $2000 = 2^45^3$ . By looking at the prime factorization of $2000$ , $c$ must have a factor of $2^4$ . If $c$ has a factor of $5^3$ , then there are two cases: either (1) $a$ or $b = 5^32^3$ , or (2) one of $a$ and $b$ has a factor of $5^3$ and the other a factor of $2^3$ . For case 1, the other number will be in the form of $2^x5^y$ , so there are $4 cdot 4 = 16$ possible such numbers; since this can be either $a$ or $b$ there are a total of $2(16)-1=31$ possibilities. For case 2, $a$ and $b$ are in the form of $2^35^x$ and $2^y5^3$ , with $x < 3$ and $y < 3$ (if they were equal to 3, it would overlap with case 1). Thus, there are $2(3 cdot 3) = 18$ cases.If $c$ does not have a factor of $5^3$ , then at least one of $a$ and $b$ must be $2^35^3$ , and both must have a factor of $5^3$ . Then, there are $4$ solutions possible just considering $a = 2^35^3$ , and a total of $4 cdot 2 - 1 = 7$ possibilities. Multiplying by three, as $0 le c le 2$ , there are $7 cdot 3 = 21$ . Together, that makes $31 + 18 + 21 = 70$ solutions for $(a, b, c)$ .
Multiplying out all of the denominators, we get: $begin{align*}104(n+k) &< 195n< 105(n+k)\ 0 &< 91n - 104k < n + kend{align*}$ Since $91n - 104k < n + k$ , $k > frac{6}{7}n$ . Also, $0 < 91n - 104k$ , so $k < frac{7n}{8}$ . Thus, $48n < 56k < 49n$ . $k$ is unique if it is within a maximum range of $112$ , so $n = 112$ .Flip all of the fractions for $[begin{array}{ccccc}frac{15}{8} &>& frac{k + n}{n} &>& frac{13}{7}\ 105n &>& 56 (k + n)& >& 104n\ 49n &>& 56k& >& 48nend{array}]$
Continue as in Solution 1.

Flip the fractions and subtract one from all sides to yield $[frac{7}{8}>frac{k}{n}>frac{6}{7}.]$ Multiply both sides by $56n$ to get $[49n>56k>48n.]$ This is equivalent to find the largest value of $n$ such that there is only one multiple of 56 within the open interval between $48n$ and $49n$ . If $n=112,$ then $98>k>96$ and $k=97$ is the unique value. For $ngeq 113,$ there is at least $(49cdot 113-48cdot 113)-1=112$ possible numbers for $k$ and there is one $k$ every 56 numbers. Hence, there must be at least two values of $k$ that work. So, the largest value of $n$ is $boxed{112}$ .
Let $PC = x$ . Since $angle APB = angle BPC = angle CPA$ , each of them is equal to $120^circ$ . By the Law of Cosines applied to triangles $triangle APB$ , $triangle BPC$ and $triangle CPA$ at their respective angles $P$ , remembering that $cos 120^circ = -frac12$ , we have $[AB^2 = 36 + 100 + 60 = 196, BC^2 = 36 + x^2 + 6x, CA^2 = 100 + x^2 + 10x]$ Then by the Pythagorean Theorem, $AB^2 + BC^2 = CA^2$ , so $[x^2 + 10x + 100 = x^2 + 6x + 36 + 196]$ and
$[4x = 132 Longrightarrow x = boxed{033}.]$
Let the total number of steps be $x$ , the speed of the escalator be $e$ and the speed of Bob be $b$ .In the time it took Bob to climb up the escalator he saw 75 steps and also climbed the entire escalator. Thus the contribution of the escalator must have been an additional $x - 75$ steps. Since Bob and the escalator were both moving at a constant speed over the time it took Bob to climb, the ratio of their distances covered is the same as the ratio of their speeds, so $frac{e}{b} = frac{x - 75}{75}$ .Similarly, in the time it took Al to walk down the escalator he saw 150 steps, so the escalator must have moved $150 - x$ steps in that time. Thus $frac{e}{3b} = frac{150 - x}{150}$ or $frac{e}{b} = frac{150 - x}{50}$ .Equating the two values of $frac{e}{b}$ we have $frac{x - 75}{75} = frac{150 - x}{50}$ and so $2x - 150 = 450 - 3x$ and $5x = 600$ and $x = 120$ , the answer.Again, let the total number of steps be $x$ , the speed of the escalator be $e$ and the speed of Bob be $b$ (all "per unit time").
Then this can be interpreted as a classic chasing problem: Bob is "behind" by $x$ steps, and since he moves at a pace of $b+e$ relative to the escalator, it will take $frac{x}{b+e}=frac{75}{e}$ time to get to the top.

Similarly, Al will take $frac{x}{3b-e}=frac{150}{e}$ time to get to the bottom.

From these two equations, we arrive at $150=frac{ex}{3b-e}=2cdot75=frac{2ex}{b+e}=frac{6ex}{3b+3e}=frac{(ex)-(6ex)}{(3b-e)-(3b+3e)}=frac{5x}{4}$ $implies600=5ximplies x=boxed{120}$ , where we have used the fact that $frac{a}{b}=frac{c}{d}=frac{apm c}{bpm d}$ (the proportion manipulations are motivated by the desire to isolate $x$ , prompting the isolation of the $150$ on one side, and the fact that if we could cancel out the $b$ 's, then the $e$ 's in the numerator and denominator would cancel out, resulting in an equation with $x$ by itself).

Let $e$ , $b$ be the speeds of the escalator and Bob, respectively.

When Al was on his way down, he took $150$ steps with a speed of $3b-e$ per step. When Bob was on his way up, he took $75$ steps with a speed of $b+e$ per step. Since Al and Bob were walking the same distance, we have $[150(3b-e)=75(b+e)]$ Solving gets the ratio $frac{e}{b}=frac{3}{5}$ .

Thus while Bob took $75$ steps to go up, the escalator has contributed an extra $frac{3}{5}cdot75=45$ steps.

Finally, there is a total of $75+45=boxed{120}$ steps in the length of the escalator.
Let us write down one such sum, with $m$ terms and first term $n + 1$ : $3^{11} = (n + 1) + (n + 2) + ldots + (n + m) = frac{1}{2} m(2n + m + 1)$ .Thus $m(2n + m + 1) = 2 cdot 3^{11}$ so $m$ is a divisor of $2cdot 3^{11}$ . However, because $n geq 0$ we have $m^2 < m(m + 1) leq 2cdot 3^{11}$ so $m < sqrt{2cdot 3^{11}} < 3^6$ . Thus, we are looking for large factors of $2cdot 3^{11}$ which are less than $3^6$ . The largest such factor is clearly $2cdot 3^5 = 486$ ; for this value of $m$ we do indeed have the valid expression $3^{11} = 122 + 123 + ldots + 607$ , for which $k=boxed{486}$ .
In order to keep $m$ as small as possible, we need to make $n$ as small as possible. $m = (n + r)^3 = n^3 + 3n^2r + 3nr^2 + r^3$ . Since $r < frac{1}{1000}$ and $m - n^3 = r(3n^2 + 3nr + r^2)$ is an integer, we must have that $3n^2 + 3nr + r^2 geq frac{1}{r} > 1000$ . This means that the smallest possible $n$ should be quite a bit smaller than 1000. In particular, $3nr + r^2$ should be less than 1, so $3n^2 > 999$ and $n > sqrt{333}$ . $18^2 = 324 < 333 < 361 = 19^2$ , so we must have $n geq 19$ . Since we want to minimize $n$ , we take $n = 19$ . Then for any positive value of $r$ , $3n^2 + 3nr + r^2 > 3cdot 19^2 > 1000$ , so it is possible for $r$ to be less than $frac{1}{1000}$ . However, we still have to make sure a sufficiently small $r$ exists.In light of the equation $m - n^3 = r(3n^2 + 3nr + r^2)$ , we need to choose $m - n^3$ as small as possible to ensure a small enough $r$ . The smallest possible value for $m - n^3$ is 1, when $m = 19^3 + 1$ . Then for this value of $m$ , $r = frac{1}{3n^2 + 3nr + r^2} < frac{1}{1000}$ , and we're set. The answer is $019$ .
If any of $r_1, ldots, r_{19}$ is larger than $r_{20}$ , one of these numbers will be compared with $r_{20}$ on the 19th step of the first bubble pass and $r_{20}$ will be moved back to the 19th position. Thus, $r_{20}$ must be the largest of the first 20 terms. In addition, $r_{20}$ must be larger than $r_{21}, r_{22}, ldots, r_{30}$ but smaller than $r_{31}$ in order that it move right to the 30th position but then not continue moving right to the 31st.Thus, our problem can be restated: What is the probability that in a sequence of 31 distinct real numbers, the largest is in position 31 and the second-largest is in position 20 (the other 29 numbers are irrelevant)?This is much easier to solve: there are $31!$ ways to order the first thirty-one numbers and $29!$ ways to arrange them so that the largest number is in the 31st position and the second-largest is in the 20th. This gives us a desired probability of $frac{29!}{31!} = frac{1}{31cdot 30} = frac{1}{930}$ , so the answer is $boxed{931}$ .
The Sophie Germain Identity states that $a^4 + 4b^4$ can be factorized as $(a^2 + 2b^2 - 2ab)(a^2 + 2b^2 + 2ab)$ . Each of the terms is in the form of $x^4 + 324$ . Using Sophie-Germain, we get that $x^4 + 4cdot 3^4 = (x^2 + 2 cdot 3^2 - 2cdot 3cdot x)(x^2 + 2 cdot 3^2 + 2cdot 3cdot x) = (x(x-6) + 18)(x(x+6)+18)$ .

$frac{[(10(10-6)+18)(10(10+6)+18)][(22(22-6)+18)(22(22+6)+18)]cdots[(58(58-6)+18)(58(58+6)+18)]}{[(4(4-6)+18)(4(4+6)+18)][(16(16-6)+18)(16(16+6)+18)]cdots[(52(52-6)+18)(52(52+6)+18)]}$

$= frac{(10(4)+18)(10(16)+18)(22(16)+18)(22(28)+18)cdots(58(52)+18)(58(64)+18)}{(4(-2)+18)(4(10)+18)(16(10)+18)(16(22)+18)cdots(52(46)+18)(52(58)+18)}$

Almost all of the terms cancel out! We are left with $frac{58(64)+18}{4(-2)+18} = frac{3730}{10} = boxed{373}$ .
Because all the triangles in the figure are similar to triangle $ABC$ , it's a good idea to use area ratios. In the diagram above, $frac {T_1}{T_3} = frac {T_2}{T_4} = frac {441}{440}.$ Hence, $T_3 = frac {440}{441}T_1$ and $T_4 = frac {440}{441}T_2$ . Additionally, the area of triangle $ABC$ is equal to both $T_1 + T_2 + 441$ and $T_3 + T_4 + T_5 + 440.$ Setting the equations equal and solving for $T_5$ , $T_5 = 1 + T_1 - T_3 + T_2 - T_4 = 1 + frac {T_1}{441} + frac {T_2}{441}$ . Therefore, $441T_5 = 441 + T_1 + T_2$ . However, $441 + T_1 + T_2$ is equal to the area of triangle $ABC$ ! This means that the ratio between the areas $T_5$ and $ABC$ is $441$ , and the ratio between the sides is $sqrt {441} = 21$ . As a result, $AB = 21sqrt {440} = sqrt {AC^2 + BC^2}$ . We now need $(AC)(BC)$ to find the value of $AC + BC$ , because $AB^2 + BC^2 + 2(AC)(BC) = (AC + BC)^2$ .Let $h$ denote the height to the hypotenuse of triangle $ABC$ . Notice that $h - frac {1}{21}h = sqrt {440}$ . (The height of $ABC$ decreased by the corresponding height of $T_5$ ) Thus, $(AB)(h) = (AC)(BC) = 22cdot 21^2$ . Because $AB^2 + BC^2 + 2(AC)(BC) = (AC + BC)^2 = 21^2cdot22^2$ , $AC + BC = (21)(22) = boxed{462}$ .Let $tanangle ABC = x$ . Now using the 1st square, $AC=21(1+x)$ and $CB=21(1+x^{-1})$ . Using the second square, $AB=sqrt{440}(1+x+x^{-1})$ . We have $AC^2+CB^2=AB^2$ , or $[441(x^2+x^{-2}+2x+2x^{-1}+2)=440(x^2+x^{-2}+2x+2x^{-1}+3).]$ Rearranging and letting $u=x+x^{-1} Rightarrow u^2 - 2 = x^2 + x^{-2}$ gives us $u^2+2u-440=0.$ We take the positive root, so $u=20$ , which means $AC+CB=21(2+x+x^{-1})=21(2+u)=boxed{462}$ .