- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1988AIME 真题及答案解析
1988AIME 真题及答案解析
答案解析请参考文末
Problem 1
One commercially available ten-button lock may be opened by depressing -- in any order -- the correct five buttons. The sample shown below has ![]() as its combination. Suppose that these locks are redesigned so that sets of as many as nine buttons or as few as one button could serve as combinations. How many additional combinations would this allow?
as its combination. Suppose that these locks are redesigned so that sets of as many as nine buttons or as few as one button could serve as combinations. How many additional combinations would this allow?

Problem 2
For any positive integer ![]() , let
, let ![]() denote the square of the sum of the digits of
denote the square of the sum of the digits of ![]() . For
. For ![]() , let
, let ![]() . Find
. Find ![]() .
.
Problem 3
Find ![]() if
if ![]() .
.
Problem 4
Suppose that ![]() for
for ![]() . Suppose further that
. Suppose further that
Problem 5
Let ![]() , in lowest terms, be the probability that a randomly chosen positive divisor of
, in lowest terms, be the probability that a randomly chosen positive divisor of ![]() is an integer multiple of
is an integer multiple of ![]() . Find
. Find ![]() .
.
Problem 6
It is possible to place positive integers into the vacant twenty-one squares of the 5 times 5 square shown below so that the numbers in each row and column form arithmetic sequences. Find the number that must occupy the vacant square marked by the asterisk (*).

Problem 7
In triangle ![]() ,
, ![]() , and the altitude from
, and the altitude from ![]() divides
divides ![]() into segments of length
into segments of length ![]() and
and ![]() . What is the area of triangle
. What is the area of triangle ![]() ?
?
Problem 8
The function ![]() , defined on the set of ordered pairs of positive integers, satisfies the following properties:
, defined on the set of ordered pairs of positive integers, satisfies the following properties: Calculate
Calculate ![]() .
.
Problem 9
Find the smallest positive integer whose cube ends in ![]() .
.
Problem 10
A convex polyhedron has for its faces 12 squares, 8 regular hexagons, and 6 regular octagons. At each vertex of the polyhedron one square, one hexagon, and one octagon meet. How many segments joining vertices of the polyhedron lie in the interior of the polyhedron rather than along an edge or a face?
Problem 11
Let ![]() be complex numbers. A line
be complex numbers. A line ![]() in the complex plane is called a mean line for the points
in the complex plane is called a mean line for the points ![]() if
if ![]() contains points (complex numbers)
contains points (complex numbers) ![]() such that
such that
Problem 12
Let ![]() be an interior point of triangle
be an interior point of triangle ![]() and extend lines from the vertices through
and extend lines from the vertices through ![]() to the opposite sides. Let
to the opposite sides. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote the lengths of the segments indicated in the figure. Find the product
denote the lengths of the segments indicated in the figure. Find the product ![]() if
if ![]() and
and ![]() .
.

Problem 13
Find ![]() if
if ![]() and
and ![]() are integers such that
are integers such that ![]() is a factor of
is a factor of ![]() .
.
Problem 14
Let ![]() be the graph of
be the graph of ![]() , and denote by
, and denote by ![]() the reflection of
the reflection of ![]() in the line
in the line ![]() . Let the equation of
. Let the equation of ![]() be written in the form
be written in the form![]() Find the product
Find the product ![]() .
.
Problem 15
In an office at various times during the day, the boss gives the secretary a letter to type, each time putting the letter on top of the pile in the secretary's in-box. When there is time, the secretary takes the top letter off the pile and types it. There are nine letters to be typed during the day, and the boss delivers them in the order 1, 2, 3, 4, 5, 6, 7, 8, 9.
While leaving for lunch, the secretary tells a colleague that letter 8 has already been typed, but says nothing else about the morning's typing. The colleague wonders which of the nine letters remain to be typed after lunch and in what order they will be typed. Based upon the above information, how many such after-lunch typing orders are possible? (That there are no letters left to be typed is one of the possibilities.)
1988AIME 详细解析
- Currently there are
 possible combinations. With any integer
possible combinations. With any integer  from
from  to
to  , the number of ways to choose a set of
, the number of ways to choose a set of  buttons is
buttons is  . Now we can use the identity
. Now we can use the identity  . So the number of additional combinations is just
. So the number of additional combinations is just  .
. - We see that






Note that this revolves between the two numbers. Since
 is even, we thus have
is even, we thus have  .
. - Raise both as exponents with base 8:

A quick explanation of the steps: On the 1st step, we use the property of logarithms that . On the 2nd step, we use the fact that
. On the 2nd step, we use the fact that  . On the 3rd step, we use the change of base formula, which states
. On the 3rd step, we use the change of base formula, which states  for arbitrary
for arbitrary  .
. - Since
 then
then![[|x_1| + |x_2| + dots + |x_n| = 19 + |x_1 + x_2 + dots + x_n| < n.]](https://latex.artofproblemsolving.com/4/7/c/47c7c53b12e318497f61229adebb8de89eecc87d.png) So
So  . We now just need to find an example where
. We now just need to find an example where  : suppose
: suppose  and
and  ; then on the left hand side we have
; then on the left hand side we have  . On the right hand side, we have
. On the right hand side, we have  , and so the equation can hold for
, and so the equation can hold for  .
.  , so it has
, so it has  factors. Out of these, we only want those factors of
factors. Out of these, we only want those factors of  which are divisible by
which are divisible by  ; it is easy to draw a bijection to the number of factors that
; it is easy to draw a bijection to the number of factors that  has, which is
has, which is  . Our probability is
. Our probability is  , and
, and  .
.- Let the coordinates of the square at the bottom left be
 , the square to the right
, the square to the right  , etc.Label the leftmost column (from bottom to top)
, etc.Label the leftmost column (from bottom to top)  and the bottom-most row (from left to right)
and the bottom-most row (from left to right)  . Our method will be to use the given numbers to set up equations to solve for
. Our method will be to use the given numbers to set up equations to solve for  and
and  , and then calculate
, and then calculate  .
.![$begin{tabular}[b]{|c|c|c|c|c|}hline 4a & & & * & \ hline 3a & 74 & & & \ hline 2a & & & & 186 \ hline a & & 103 & & \ hline 0 & b & 2b & 3b & 4b \ hline end{tabular}$](https://latex.artofproblemsolving.com/1/0/4/104fc90c8563631420a18e19eda82246ea0c2216.png) We can compute the squares at the intersections of two existing numbers in terms of
We can compute the squares at the intersections of two existing numbers in terms of  and
and  ; two such equations will give us the values of
; two such equations will give us the values of  and
and  . On the fourth row from the bottom, the common difference is
. On the fourth row from the bottom, the common difference is  , so the square at
, so the square at  has a value of
has a value of  . On the third column from the left, the common difference is
. On the third column from the left, the common difference is  , so that square also has a value of
, so that square also has a value of  . Equating, we get
. Equating, we get  .Now we compute the square
.Now we compute the square  . By rows, this value is simply the average of
. By rows, this value is simply the average of  and
and  , so it is equal to
, so it is equal to  . By columns, the common difference is
. By columns, the common difference is  , so our value is
, so our value is  . Equating,
. Equating,  .Solving
.Solving
gives
 ,
,  . Now it is simple to calculate
. Now it is simple to calculate  . One way to do it is to see that
. One way to do it is to see that  has
has  and
and  has
has  , so
, so  has
has  . Now,
. Now,  has
has  , so
, so  .
.First, let
 the number to be placed in the first column, fourth row. Let
the number to be placed in the first column, fourth row. Let  the number to be placed in the second column, fifth row. We can determine the entire first column and fifth row in terms of
the number to be placed in the second column, fifth row. We can determine the entire first column and fifth row in terms of  and
and  :
:![$begin{tabular}[b]{|c|c|c|c|c|}hline 4a & & & & \ hline 3a & & & & \ hline 2a & & & & \ hline a & & & & \ hline 0 & b & 2b & 3b & 4b \ hline end{tabular}$](https://latex.artofproblemsolving.com/b/5/5/b55971033f002187dc3608de8418553995b731ad.png)
Next, let
 the number to be placed in the second column, fourth row. We can determine the entire second column and fourth row in terms of
the number to be placed in the second column, fourth row. We can determine the entire second column and fourth row in terms of  ,
,  , and
, and  :
:![$begin{tabular}[b]{|c|c|c|c|c|}hline 4a & 4a + b + 4c & & & \ hline 3a & 3a + b + 3c & & & \ hline 2a & 2a + b + 2c & & & \ hline a & a + b + c & a + 2b + 2c & a + 3b + 3c & a + 4b + 4c \ hline 0 & b & 2b & 3b & 4b \ hline end{tabular}$](https://latex.artofproblemsolving.com/0/6/c/06ce47c5f90d3bb1943a6a4b35d55b0f485f9862.png)
We have now determined at least two values in each row and column. We can finish the table without introducing any more variables:
![$begin{tabular}[b]{|c|c|c|c|c|}hline 4a & 4a + b + 4c & 4a + 2b + 8c & 4a + 3b + 12c & 4a + 4b + 16c \ hline 3a & 3a + b + 3c & 3a + 2b + 6c & 3a + 3b + 9c & 3a + 4b + 12c \ hline 2a & 2a + b + 2c & 2a + 2b + 4c & 2a + 3b + 6c & 2a + 4b + 8c \ hline a & a + b + c & a + 2b + 2c & a + 3b + 3c & a + 4b + 4c \ hline 0 & b & 2b & 3b & 4b \ hline end{tabular}$](https://latex.artofproblemsolving.com/5/d/b/5dbaa0d43ee82319311a26263eed54f5970701f0.png)
We now have a system of equations.



Solving, we find that
 . The number in the square marked by the asterisk is
. The number in the square marked by the asterisk is 
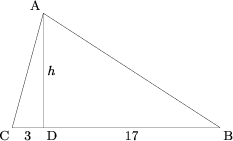
 be the intersection of the altitude with
be the intersection of the altitude with  , and
, and  be the length of the altitude. Without loss of generality, let
be the length of the altitude. Without loss of generality, let  and
and  . Then
. Then  and
and  . Using the tangent sum formula,
. Using the tangent sum formula, The positive value of
The positive value of  is
is  , so the area is
, so the area is  .
.- Since all of the function's properties contain a recursive definition except for the first one, we know that
 in order to obtain an integer answer. So, we have to transform
in order to obtain an integer answer. So, we have to transform  to this form by exploiting the other properties. The second one doesn't help us immediately, so we will use the third one.Note that
to this form by exploiting the other properties. The second one doesn't help us immediately, so we will use the third one.Note that![[f(14,52) = f(14,14 + 38) = frac {52}{38}f(14,38)]](https://latex.artofproblemsolving.com/3/a/8/3a8251ad5c97e5ba8f099a0cf447782856afff7e.png) Repeating the process several times,
Repeating the process several times, Notice that
Notice that  satisfies all three properties:Clearly,
satisfies all three properties:Clearly,  and
and  .
.
Using the identities
 and
and  , we have:
, we have:


 .
.Hence,
 is a solution to the functional equation.
is a solution to the functional equation.Since this is an AIME problem, there is exactly one correct answer, and thus, exactly one possible value of
 .
.Therefore,
 .
. - A little bit of checking tells us that the units digit must be 2. Now our cube must be in the form of
 ; using the binomial theorem gives us
; using the binomial theorem gives us  . Since we are looking for the tens digit,
. Since we are looking for the tens digit,  we get
we get  . This is true if the tens digit is either
. This is true if the tens digit is either  or
or  . Casework:
. Casework:
 : Then our cube must be in the form of
: Then our cube must be in the form of  . Hence the lowest possible value for the hundreds digit is
. Hence the lowest possible value for the hundreds digit is  , and so
, and so  is a valid solution.
is a valid solution. : Then our cube is
: Then our cube is  . The lowest possible value for the hundreds digit is
. The lowest possible value for the hundreds digit is  , and we get
, and we get  . Hence, since
. Hence, since  , the answer is
, the answer is 
 and
and  .
.  due to the last digit of
due to the last digit of  . Let
. Let  . By expanding,
. By expanding,  .
.By looking at the last digit again, we see
 , so we let
, so we let  where
where  . Plugging this in to
. Plugging this in to  gives
gives  . Obviously,
. Obviously,  , so we let
, so we let  where
where  can be any non-negative integer.
can be any non-negative integer.Therefore,
 .
.  must also be a multiple of
must also be a multiple of  , so
, so  . Therefore, the minimum of
. Therefore, the minimum of  is
is  .
.Let
 . We factor an
. We factor an  out of the right hand side, and we note that
out of the right hand side, and we note that  must be of the form
must be of the form  , where
, where  is a positive integer. Then, this becomes
is a positive integer. Then, this becomes  . Taking mod
. Taking mod  ,
,  , and
, and  , we get
, we get  ,
,  , and
, and  .
.We can work our way up, and find that
 ,
,  , and finally
, and finally  . This gives us our smallest value,
. This gives us our smallest value,  , so
, so  , as desired. - Spacesam
, as desired. - Spacesam - The number of segments joining the vertices of the polyhedron is
 . We must now subtract out those segments that lie along an edge or a face.Since every vertex of the polyhedron lies on exactly one vertex of a square/hexagon/octagon, we have that
. We must now subtract out those segments that lie along an edge or a face.Since every vertex of the polyhedron lies on exactly one vertex of a square/hexagon/octagon, we have that  .Each vertex is formed by the intersection of 3 edges. Since every edge is counted twice, once at each of its endpoints, the number of edges
.Each vertex is formed by the intersection of 3 edges. Since every edge is counted twice, once at each of its endpoints, the number of edges  is
is  .Each of the segments lying on a face of the polyhedron must be a diagonal of that face. Each square contributes
.Each of the segments lying on a face of the polyhedron must be a diagonal of that face. Each square contributes  diagonals, each hexagon
diagonals, each hexagon  , and each octagon
, and each octagon  . The number of diagonals is thus
. The number of diagonals is thus  .Subtracting, we get that the number of space diagonals is
.Subtracting, we get that the number of space diagonals is  .We first find the number of vertices on the polyhedron: There are 4 corners per square, 6 corners per hexagon, and 8 corners per octagon. Each vertex is where 3 corners coincide, so we count the corners and divide by 3.
.We first find the number of vertices on the polyhedron: There are 4 corners per square, 6 corners per hexagon, and 8 corners per octagon. Each vertex is where 3 corners coincide, so we count the corners and divide by 3.  .
.
We know that all vertices look the same (from the problem statement), so we should find the number of line segments originating from a vertex, and multiply that by the number of vertices, and divide by 2 (because each space diagonal is counted twice because it has two endpoints).
Counting the vertices that are on the same face as an arbitrary vertex, we find that there are 13 vertices that aren't possible endpoints of a line originating from the vertex in the middle of the diagram. You can draw a diagram to count this better:
 Since 13 aren't possible endpoints, that means that there are 35 possible endpoints per vertex. The total number of segments joining vertices that aren't on the same face is
Since 13 aren't possible endpoints, that means that there are 35 possible endpoints per vertex. The total number of segments joining vertices that aren't on the same face is 

 Each
Each  lies on the complex line
lies on the complex line  , so we can rewrite this as
, so we can rewrite this as
 Matching the real parts and the imaginary parts, we get that
Matching the real parts and the imaginary parts, we get that  and
and  . Simplifying the second summation, we find that
. Simplifying the second summation, we find that  , and substituting, the answer is
, and substituting, the answer is  .
.- Call the cevians AD, BE, and CF. Using area ratios (
 and
and  have the same base), we have:
have the same base), we have:![$frac {d}{a + d} = frac {[PBC]}{[ABC]}$](https://latex.artofproblemsolving.com/6/d/4/6d4ac85ad425625a41e117bcae717d10e8ad5d1a.png) Similarily,
Similarily, ![$frac {d}{b + d} = frac {[PCA]}{[ABC]}$](https://latex.artofproblemsolving.com/4/7/f/47f2d984035fbfe5e48d693e2e43b890e55a66e5.png) and
and ![$frac {d}{c + d} = frac {[PAB]}{[ABC]}$](https://latex.artofproblemsolving.com/5/4/a/54a5ecd6c3fa66bde1006a9a6a15a21e7b1a234b.png) .Then,
.Then, ![$frac {d}{a + d} + frac {d}{b + d} + frac {d}{c + d} = frac {[PBC]}{[ABC]} + frac {[PCA]}{[ABC]} + frac {[PAB]}{[ABC]} = frac {[ABC]}{[ABC]} = 1$](https://latex.artofproblemsolving.com/1/0/4/1040a096ae433a59a04030b2b89c285891454e8a.png) The identity
The identity  is a form of Ceva's Theorem.Plugging in
is a form of Ceva's Theorem.Plugging in  , we get
, we get
![[frac{3}{a + 3} + frac{3}{b + 3} + frac{3}{c+3} = 1]](https://latex.artofproblemsolving.com/b/d/3/bd305fd0d0e48ac0b0330975c426104c87c34e3e.png)
![[3[(a + 3)(b + 3) + (b + 3)(c + 3) + (c + 3)(a + 3)] = (a+3)(b+3)(c+3)]](https://latex.artofproblemsolving.com/4/0/9/4092762dabdb65624284e3cfe4b786c2f2d9bec3.png)
![[3(ab + bc + ca) + 18(a + b + c) + 81 = abc + 3(ab + bc + ca) + 9(a + b + c) + 27]](https://latex.artofproblemsolving.com/5/1/6/5164a27c882483f2b05ae9bff9d3109389210a11.png)
![[9(a + b + c) + 54 = abc=boxed{441}]](https://latex.artofproblemsolving.com/5/8/5/585be2e21d8c019bb5b64a5c1099ff541eef256c.png)
- Let's work backwards! Let
 and let
and let  be the polynomial such that
be the polynomial such that  .Clearly, the constant term of
.Clearly, the constant term of  must be
must be  . Now, we have
. Now, we have  , where
, where  is some coefficient. However, since
is some coefficient. However, since  has no
has no  term, it must be true that
term, it must be true that  .Let's find
.Let's find  now. Notice that all we care about in finding
now. Notice that all we care about in finding  is that
is that  . Therefore,
. Therefore,  . Undergoing a similar process,
. Undergoing a similar process,  ,
,  ,
,  , and we see a nice pattern. The coefficients of
, and we see a nice pattern. The coefficients of  are just the Fibonacci sequence with alternating signs! Therefore,
are just the Fibonacci sequence with alternating signs! Therefore,  , where
, where  denotes the 16th Fibonnaci number and
denotes the 16th Fibonnaci number and  .
. - Given a point
 on
on  , we look to find a formula for
, we look to find a formula for  on
on  . Both points lie on a line that is perpendicular to
. Both points lie on a line that is perpendicular to  , so the slope of
, so the slope of  is
is  . Thus
. Thus  . Also, the midpoint of
. Also, the midpoint of  ,
,  , lies on the line
, lies on the line  . Therefore
. Therefore  .Solving these two equations, we find
.Solving these two equations, we find  and
and  . Substituting these points into the equation of
. Substituting these points into the equation of  , we get
, we get  , which when expanded becomes
, which when expanded becomes  .Thus,
.Thus,  .
. - Re-stating the problem for clarity, let
 be a set arranged in increasing order. At any time an element can be appended to the end of
be a set arranged in increasing order. At any time an element can be appended to the end of  , or the last element of
, or the last element of  can be removed. The question asks for the number of different orders in which the all of the remaining elements of
can be removed. The question asks for the number of different orders in which the all of the remaining elements of  can be removed, given that
can be removed, given that  had been removed already.
had been removed already.
Since
 had already been added to the pile, the numbers
had already been added to the pile, the numbers  had already been added at some time to the pile;
had already been added at some time to the pile;  might or might not have been added yet. So currently
might or might not have been added yet. So currently  is a subset of
is a subset of  , possibly with
, possibly with  at the end. Given that
at the end. Given that  has
has  elements, there are
elements, there are  intervals for
intervals for  to be inserted, or
to be inserted, or  might have already been placed, giving
might have already been placed, giving  different possibilities.
different possibilities.Thus, the answer is


 .
.
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









