Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

1992AIME 真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月12日上午11:22

1992AIME 真题及答案解析

答案解析请参考文末

Problem 1

Find the sum of all positive rational numbers that are less than 10 and that have denominator 30 when written in lowest terms.

Problem 2

A positive integer is called ascending if, in its decimal representation, there are at least two digits and each digit is less than any digit to its right. How many ascending positive integers are there?

Problem 3

A tennis player computes her win ratio by dividing the number of matches she has won by the total number of matches she has played. At the start of a weekend, her win ratio is exactly $.500$ . During the weekend, she plays four matches, winning three and losing one. At the end of the weekend, her win ratio is greater than $.503$ . What's the largest number of matches she could've won before the weekend began?

Problem 4

In Pascal's Triangle, each entry is the sum of the two entries above it. In which row of Pascal's Triangle do three consecutive entries occur that are in the ratio $3: 4: 5$ ?

Problem 5

Let $S^{}_{}$ be the set of all rational numbers $r^{}_{}$ , $0^{}_{}<r<1$ , that have a repeating decimal expansion in the form $0.abcabcabcldots=0.overline{abc}$ , where the digits $a^{}_{}$ , $b^{}_{}$ , and $c^{}_{}$ are not necessarily distinct. To write the elements of $S^{}_{}$ as fractions in lowest terms, how many different numerators are required?

Problem 6

For how many pairs of consecutive integers in ${1000,1001,1002^{}_{},ldots,2000}$ is no carrying required when the two integers are added?

Problem 7

Faces $ABC^{}_{}$ and $BCD^{}_{}$ of tetrahedron $ABCD^{}_{}$ meet at an angle of $30^circ$ . The area of face $ABC^{}_{}$ is $120^{}_{}$ , the area of face $BCD^{}_{}$ is $80^{}_{}$ , and $BC=10^{}_{}$ . Find the volume of the tetrahedron.

Problem 8

For any sequence of real numbers $A=(a_1,a_2,a_3,ldots)$ , define $Delta A^{}_{}$ to be the sequence $(a_2-a_1,a_3-a_2,a_4-a_3,ldots)$ , whose $n^{th}$ term is $a_{n+1}-a_n^{}$ . Suppose that all of the terms of the sequence $Delta(Delta A^{}_{})$ are $1^{}_{}$ , and that $a_{19}=a_{92}^{}=0$ . Find $a_1^{}$ .

Problem 9

Trapezoid $ABCD^{}_{}$ has sides $AB=92^{}_{}$ , $BC=50^{}_{}$ , $CD=19^{}_{}$ , and $AD=70^{}_{}$ , with $AB^{}_{}$ parallel to $CD^{}_{}$ . A circle with center $P^{}_{}$ on $AB^{}_{}$ is drawn tangent to $BC^{}_{}$ and $AD^{}_{}$ . Given that $AP^{}_{}=frac mn$ , where $m^{}_{}$ and $n^{}_{}$ are relatively prime positive integers, find $m+n^{}_{}$ .

Problem 10

Consider the region $A^{}_{}$ in the complex plane that consists of all points $z^{}_{}$ such that both $frac{z^{}_{}}{40}$ and $frac{40^{}_{}}{overline{z}}$ have real and imaginary parts between $0^{}_{}$ and $1^{}_{}$ , inclusive. What is the integer that is nearest the area of $A^{}_{}$ ?

Problem 11

Lines $l_1^{}$ and $l_2^{}$ both pass through the origin and make first-quadrant angles of $frac{pi}{70}$ and $frac{pi}{54}$ radians, respectively, with the positive x-axis. For any line $l^{}_{}$ , the transformation $R(l)^{}_{}$ produces another line as follows: $l^{}_{}$ is reflected in $l_1^{}$ , and the resulting line is reflected in $l_2^{}$ . Let $R^{(1)}(l)=R(l)^{}_{}$ and $R^{(n)}(l)^{}_{}=Rleft(R^{(n-1)}(l)right)$ . Given that $l^{}_{}$ is the line $y=frac{19}{92}x^{}_{}$ , find the smallest positive integer $m^{}_{}$ for which $R^{(m)}(l)=l^{}_{}$ .

Problem 12

In a game of Chomp, two players alternately take bites from a 5-by-7 grid of unit squares. To take a bite, a player chooses one of the remaining squares, then removes ("eats") all squares in the quadrant defined by the left edge (extended upward) and the lower edge (extended rightward) of the chosen square. For example, the bite determined by the shaded square in the diagram would remove the shaded square and the four squares marked by $times.$ (The squares with two or more dotted edges have been removed from the original board in previous moves.)

AIME 1992 Problem 12.png

The object of the game is to make one's opponent take the last bite. The diagram shows one of the many subsets of the set of 35 unit squares that can occur during the game of Chomp. How many different subsets are there in all? Include the full board and empty board in your count.

Problem 13

Triangle $ABC^{}_{}$ has $AB=9^{}_{}$ and $BC: AC=40: 41^{}_{}$ . What's the largest area that this triangle can have?

Problem 14

In triangle $ABC^{}_{}$ , $A'$ , $B'$ , and $C'$ are on the sides $BC$ , $AC^{}_{}$ , and $AB^{}_{}$ , respectively. Given that $AA'$ , $BB'$ , and $CC'$ are concurrent at the point $O^{}_{}$ , and that $frac{AO^{}_{}}{OA'}+frac{BO}{OB'}+frac{CO}{OC'}=92$ , find $frac{AO}{OA'}cdot frac{BO}{OB'}cdot frac{CO}{OC'}$ .

Problem 15

Define a positive integer $n^{}_{}$ to be a factorial tail if there is some positive integer $m^{}_{}$ such that the decimal representation of $m!$ ends with exactly $n$ zeroes. How many positive integers less than $1992$ are not factorial tails?

1992AIME 详细解析

There are 8 fractions which fit the conditions between 0 and 1: $frac{1}{30},frac{7}{30},frac{11}{30},frac{13}{30},frac{17}{30},frac{19}{30},frac{23}{30},frac{29}{30}$ Their sum is 4. Note that there are also 8 terms between 1 and 2 which we can obtain by adding 1 to each of our first 8 terms. For example, $1+frac{19}{30}=frac{49}{30}.$ Following this pattern, our answer is $4(10)+8(1+2+3+cdots+9)=boxed{400}.$
Note that an ascending number is exactly determined by its digits: for any set of digits (not including 0, since the only position for 0 is at the leftmost end of the number, i.e. a leading 0), there is exactly one ascending number with those digits.So, there are nine digits that may be used: $1,2,3,4,5,6,7,8,9.$ Note that each digit may be present or may not be present. Hence, there are $2^9=512$ potential ascending numbers, one for each subset of ${1, 2, 3, 4, 5, 6, 7, 8, 9}$ .However, we've counted one-digit numbers and the empty set, so we must subtract them off to get our answer, $512-10=boxed{502}.$
Let $n$ be the number of matches won, so that $frac{n}{2n}=frac{1}{2}$ , and $frac{n+3}{2n+4}>frac{503}{1000}$ . Cross multiplying, $1000n+3000>1006n+2012$ , and $n<frac{988}{6}$ . Thus, the answer is $boxed{164}$ .
In Pascal's Triangle, we know that the binomial coefficients of the $n$ th row are $binom{n} {0}, binom{n}{1}, ..., binom{n} {n}$ . Let our row be the $n$ th row such that the three consecutive entries are $binom{n} {r-1}$ , $binom{n}{r}$ and $binom{n} {r+1}$ . (We consider $r-1, r, r+1$ because it cancels stuff out easier)Consider what $binom{n}{r}$ equals to in a more explicit form. It equals $frac{n!}{(n-r)!r!}$ .Now consider what it means to have three consecutive entries occurring in the ratio $3:4:5$ . It means that we will have $frac{binom{n}{r-1}}{3} = frac{binom{n}{r}}{4} = frac{binom{n}{r+1}}{5}$ . Note that the order of the ratio does not matter, as ascending from one side of Pascal's triangle is equivalent to descending from the opposite side of Pascal's triangle. We can multiply by a LCM of $60$ to further simplify the problem into $20binom{n}{r-1} = 15binom{n}{r} = 12binom{n}{r+1}$ Using the more explicit form of $binom{n}{r}$ , we see that this equivalence function collapses into $frac{20*n!*r}{(n-r+1)(n-r)!r!} = frac{15*n!}{(n-r)!r!} = frac{12*n!*(n-r)}{(n-r)!r!(r+1)}$ (all of which is given by plugging in $r-1, r, r+1$ into $frac{n!}{(n-r)!r!}$ )
After canceling out the $n!$ in the numerator and the $(n-r)!r!$ in the denominator, we get $frac{20r}{n-r+1} = 15 = frac{12(n-r)}{r+1}$ . Setting the first equation to $15$ and the third equation to $15$ , we get a system that is solvable. We have: $[20r = 15n - 15r + 15 Rightarrow 35r - 15n = 15]$ $[15r + 15 = 12n - 12r Rightarrow 27r - 12n = -15]$

Solving these equations, we get that $r = 27$ and $n = 62$ . Our goal is to find which row of Pascal's triangle this ratio occurs, or in other words find what n is, which we conclude to be $boxed{62}$
We consider the method in which repeating decimals are normally converted to fractions with an example: $x=0.overline{176}$ $Rightarrow 1000x=176.overline{176}$ $Rightarrow 999x=1000x-x=176$
$Rightarrow x=frac{176}{999}$

Thus, let $x=0.overline{abc}$

$Rightarrow 1000x=abc.overline{abc}$

$Rightarrow 999x=1000x-x=abc$

$Rightarrow x=frac{abc}{999}$

If $abc$ is not divisible by $3$ or $37$ , then this is in lowest terms. Let us consider the other multiples: $333$ multiples of $3$ , $27$ of $37$ , and $9$ of $3$ and $37$ , so $999-333-27+9 = 648$ , which is the amount that are neither. The $12$ numbers that are multiples of $81$ reduce to multiples of $3$ . We have to count these since it will reduce to a multiple of $3$ which we have removed from $999$ , but, this cannot be removed since the numerator cannot cancel the $3$ .There aren't any numbers which are multiples of $37^2$ , so we can't get numerators which are multiples of $37$ . Therefore $648 + 12 = boxed{660}$ .
Consider what carrying means: If carrying is needed to add two numbers with digits $abcd$ and $efgh$ , then $h+dge 10$ or $c+gge 10$ or $b+fge 10$ . 6. Consider $c in {0, 1, 2, 3, 4}$ . $1abc + 1ab(c+1)$ has no carry if $a, b in {0, 1, 2, 3, 4}$ . This gives $5^3=125$ possible solutions.With $c in {5, 6, 7, 8}$ , there obviously must be a carry. Consider $c = 9$ . $a, b in {0, 1, 2, 3, 4}$ have no carry. This gives $5^2=25$ possible solutions. Considering $b = 9$ , $a in {0, 1, 2, 3, 4, 9}$ have no carry. Thus, the solution is $125 + 25 + 6=boxed{156}$ .
Since the area $BCD=80=frac{1}{2}cdot10cdot16$ , the perpendicular from $D$ to $BC$ has length $16$ .The perpendicular from $D$ to $ABC$ is $16 cdot sin 30^circ=8$ . Therefore, the volume is $frac{8cdot120}{3}=boxed{320}$ .
Note that the $Delta$ s are reminiscent of differentiation; from the condition $Delta(Delta{A}) = 1$ , we are led to consider the differential equation $[frac{d^2 A}{dn^2} = 1]$ This inspires us to guess a quadratic with leading coefficient 1/2 as the solution; $[a_{n} = frac{1}{2}(n-19)(n-92)]$ as we must have roots at $n = 19$ and $n = 92$ .Thus, $a_1=frac{1}{2}(1-19)(1-92)=boxed{819}$ .
Let $AP=x$ so that $PB=92-x.$ Extend $AD, BC$ to meet at $X,$ and note that $XP$ bisects $angle AXB;$ let it meet $CD$ at $E.$ Using the angle bisector theorem, we let $XB=y(92-x), XA=xy$ for some $y.$ Then $XD=xy-70, XC=y(92-x)-50,$ thus $[frac{xy-70}{y(92-x)-50} = frac{XD}{XC} = frac{ED}{EC}=frac{AP}{PB} = frac{x}{92-x},]$ which we can rearrange, expand and cancel to get $120x=70cdot 92,$ hence $AP=x=frac{161}{3}.$
Let $z=a+bi implies frac{z}{40}=frac{a}{40}+frac{b}{40}i$ . Since $0leq frac{a}{40},frac{b}{40}leq 1$ we have the inequality $[0leq a,b leq 40]$ which is a square of side length $40$ .Also, $frac{40}{overline{z}}=frac{40}{a-bi}=frac{40a}{a^2+b^2}+frac{40b}{a^2+b^2}i$ so we have $0leq a,b leq frac{a^2+b^2}{40}$ , which leads to: $[(a-20)^2+b^2geq 20^2]$ $[a^2+(b-20)^2geq 20^2]$ We graph them:To find the area outside the two circles but inside the square, we want to find the unique area of the two circles. We can do this by adding the area of the two circles and then subtracting out their overlap. There are two methods of finding the area of overlap:
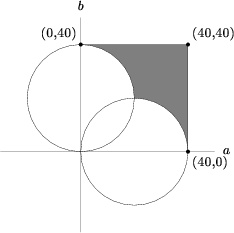
1. Consider that the area is just the quarter-circle with radius $20$ minus an isosceles right triangle with base length $20$ , and then doubled (to consider the entire overlapped area)

2. Consider that the circles can be converted into polar coordinates, and their equations are $r = 40sintheta$ and $r = 40costheta$ . Using calculus with the appropriate bounds, we can compute the overlapped area.

Using either method, we compute the overlapped area to be $200pi + 400$ , and so the area of the intersection of those three graphs is $40^2-(200pi + 400) Rightarrow 1200 - 200pi approx 571.68$

$boxed{572}$
Let $l$ be a line that makes an angle of $theta$ with the positive $x$ -axis. Let $l'$ be the reflection of $l$ in $l_1$ , and let $l''$ be the reflection of $l'$ in $l_2$ .The angle between $l$ and $l_1$ is $theta - frac{pi}{70}$ , so the angle between $l_1$ and $l'$ must also be $theta - frac{pi}{70}$ . Thus, $l'$ makes an angle of $frac{pi}{70}-left(theta-frac{pi}{70}right) = frac{pi}{35}-theta$ with the positive $x$ -axis.Similarly, since the angle between $l'$ and $l_2$ is $left(frac{pi}{35}-thetaright)-frac{pi}{54}$ , the angle between $l''$ and the positive $x$ -axis is $frac{pi}{54}-left(left(frac{pi}{35}-thetaright)-frac{pi}{54}right) = frac{pi}{27}-frac{pi}{35}+theta = frac{8pi}{945} + theta$ .Thus, $R(l)$ makes an $frac{8pi}{945} + theta$ angle with the positive $x$ -axis. So $R^{(n)}(l)$ makes an $frac{8npi}{945} + theta$ angle with the positive $x$ -axis.
Therefore, $R^{(m)}(l)=l$ iff $frac{8mpi}{945}$ is an integral multiple of $pi$ . Thus, $8m equiv 0pmod{945}$ . Since $gcd(8,945)=1$ , $m equiv 0 pmod{945}$ , so the smallest positive integer $m$ is $boxed{945}$ .
By drawing possible examples of the subset, one can easily see that making one subset is the same as dividing the game board into two parts.One can also see that it is the same as finding the shortest route from the upper left hand corner to the lower right hand corner; Such a route would require 5 lengths that go down, and 7 that go across, with the shape on the right "carved" out by the path a possible subset.Therefore, the total number of such paths is $binom{12}{5}=boxed{792}$
First, consider the triangle in a coordinate system with vertices at $(0,0)$ , $(9,0)$ , and $(a,b)$ . Applying the distance formula, we see that $frac{ sqrt{a^2 + b^2} }{ sqrt{ (a-9)^2 + b^2 } } = frac{40}{41}$ .We want to maximize $b$ , the height, with $9$ being the base.Simplifying gives $-a^2 -frac{3200}{9}a +1600 = b^2$ .To maximize $b$ , we want to maximize $b^2$ . So if we can write: $b^2=-(a+n)^2+m$ , then $m$ is the maximum value of $b^2$ (this follows directly from the trivial inequality, because if ${x^2 ge 0}$ then plugging in $a+n$ for $x$ gives us ${(a+n)^2 ge 0}$ ).
$b^2=-a^2 -frac{3200}{9}a +1600=-left(a +frac{1600}{9}right)^2 +1600+left(frac{1600}{9}right)^2$ .

$Rightarrow blesqrt{1600+left(frac{1600}{9}right)^2}=40sqrt{1+frac{1600}{81}}=frac{40}{9}sqrt{1681}=frac{40cdot 41}{9}$ .

Then the area is $9cdotfrac{1}{2} cdot frac{40cdot 41}{9} = boxed{820}$ .
Let $K_A=[BOC], K_B=[COA],$ and $K_C=[AOB].$ Due to triangles $BOC$ and $ABC$ having the same base, $[frac{AO}{OA'}+1=frac{AA'}{OA'}=frac{[ABC]}{[BOC]}=frac{K_A+K_B+K_C}{K_A}.]$ Therefore, we have $[frac{AO}{OA'}=frac{K_B+K_C}{K_A}]$ $[frac{BO}{OB'}=frac{K_A+K_C}{K_B}]$ $[frac{CO}{OC'}=frac{K_A+K_B}{K_C}.]$ Thus, we are given $[frac{K_B+K_C}{K_A}+frac{K_A+K_C}{K_B}+frac{K_A+K_B}{K_C}=92.]$ Combining and expanding gives $[frac{K_A^2K_B+K_AK_B^2+K_A^2K_C+K_AK_C^2+K_B^2K_C+K_BK_C^2}{K_AK_BK_C}=92.]$ We desire $frac{(K_B+K_C)(K_C+K_A)(K_A+K_B)}{K_AK_BK_C}.$ Expanding this gives $[frac{K_A^2K_B+K_AK_B^2+K_A^2K_C+K_AK_C^2+K_B^2K_C+K_BK_C^2}{K_AK_BK_C}+2=boxed{094}.]$
Let the number of zeros at the end of $m!$ be $f(m)$ . We have $f(m) = leftlfloor frac{m}{5} rightrfloor + leftlfloor frac{m}{25} rightrfloor + leftlfloor frac{m}{125} rightrfloor + leftlfloor frac{m}{625} rightrfloor + leftlfloor frac{m}{3125} rightrfloor + cdots$ .Note that if $m$ is a multiple of $5$ , $f(m) = f(m+1) = f(m+2) = f(m+3) = f(m+4)$ .Since $f(m) le frac{m}{5} + frac{m}{25} + frac{m}{125} + cdots = frac{m}{4}$ , a value of $m$ such that $f(m) = 1991$ is greater than $7964$ . Testing values greater than this yields $f(7975)=1991$ .There are $frac{7975}{5} = 1595$ distinct positive integers, $f(m)$ , less than $1992$ . Thus, there are $1991-1595 = boxed{396}$ positive integers less than $1992$ that are not factorial tails.