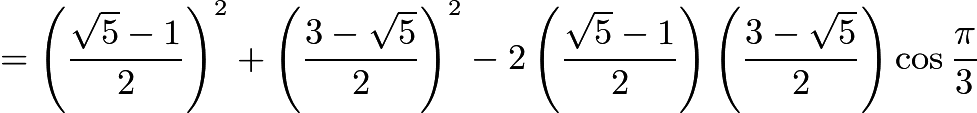- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1998AIME 真题及答案解析
1998AIME 真题及答案解析
答案解析请参考文末
Problem 1
For how many values of ![]() is
is ![]() the least common multiple of the positive integers
the least common multiple of the positive integers ![]() and
and ![]() , and
, and ![]() ?
?
Problem 2
Find the number of ordered pairs ![]() of positive integers that satisfy
of positive integers that satisfy ![]() and
and ![]() .
.
Problem 3
The graph of ![]() partitions the plane into several regions. What is the area of the bounded region?
partitions the plane into several regions. What is the area of the bounded region?
Problem 4
Nine tiles are numbered ![]() respectively. Each of three players randomly selects and keeps three of the tiles, and sums those three values. The probability that all three players obtain an odd sum is
respectively. Each of three players randomly selects and keeps three of the tiles, and sums those three values. The probability that all three players obtain an odd sum is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 5
Given that ![]() find
find ![]()
Problem 6
Let ![]() be a parallelogram. Extend
be a parallelogram. Extend ![]() through
through ![]() to a point
to a point ![]() and let
and let ![]() meet
meet ![]() at
at ![]() and
and ![]() at
at ![]() Given that
Given that ![]() and
and ![]() find
find ![]()
Problem 7
Let ![]() be the number of ordered quadruples
be the number of ordered quadruples ![]() of positive odd integers that satisfy
of positive odd integers that satisfy  Find
Find ![]()
Problem 8
Except for the first two terms, each term of the sequence ![]() is obtained by subtracting the preceding term from the one before that. The last term of the sequence is the first negative term encountered. What positive integer
is obtained by subtracting the preceding term from the one before that. The last term of the sequence is the first negative term encountered. What positive integer ![]() produces a sequence of maximum length?
produces a sequence of maximum length?
Problem 9
Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between 9 a.m. and 10 a.m., and stay for exactly ![]() minutes. The probability that either one arrives while the other is in the cafeteria is
minutes. The probability that either one arrives while the other is in the cafeteria is ![]() and
and ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
Problem 10
Eight spheres of radius 100 are placed on a flat surface so that each sphere is tangent to two others and their centers are the vertices of a regular octagon. A ninth sphere is placed on the flat surface so that it is tangent to each of the other eight spheres. The radius of this last sphere is ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Problem 11
Three of the edges of a cube are ![]() and
and ![]() and
and ![]() is an interior diagonal. Points
is an interior diagonal. Points ![]() and
and ![]() are on
are on ![]() and
and ![]() respectively, so that
respectively, so that ![]() and
and ![]() What is the area of the polygon that is the intersection of plane
What is the area of the polygon that is the intersection of plane ![]() and the cube?
and the cube?
Problem 12
Let ![]() be equilateral, and
be equilateral, and ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively. There exist points
respectively. There exist points ![]() and
and ![]() on
on ![]() and
and ![]() respectively, with the property that
respectively, with the property that ![]() is on
is on ![]() is on
is on ![]() and
and ![]() is on
is on ![]() The ratio of the area of triangle
The ratio of the area of triangle ![]() to the area of triangle
to the area of triangle ![]() is
is ![]() where
where ![]() and
and ![]() are integers, and
are integers, and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]() ?
?
Problem 13
If ![]() is a set of real numbers, indexed so that
is a set of real numbers, indexed so that ![]() its complex power sum is defined to be
its complex power sum is defined to be ![]() where
where ![]() Let
Let ![]() be the sum of the complex power sums of all nonempty subsets of
be the sum of the complex power sums of all nonempty subsets of ![]() Given that
Given that ![]() and
and ![]() where
where ![]() and
and ![]() are integers, find
are integers, find ![]()
Problem 14
An ![]() rectangular box has half the volume of an
rectangular box has half the volume of an ![]() rectangular box, where
rectangular box, where ![]() and
and ![]() are integers, and
are integers, and ![]() What is the largest possible value of
What is the largest possible value of ![]() ?
?
Problem 15
Define a domino to be an ordered pair of distinct positive integers. A proper sequence of dominos is a list of distinct dominos in which the first coordinate of each pair after the first equals the second coordinate of the immediately preceding pair, and in which ![]() and
and ![]() do not both appear for any
do not both appear for any ![]() and
and ![]() . Let
. Let ![]() be the set of all dominos whose coordinates are no larger than 40. Find the length of the longest proper sequence of dominos that can be formed using the dominos of
be the set of all dominos whose coordinates are no larger than 40. Find the length of the longest proper sequence of dominos that can be formed using the dominos of ![]()
1998AIME 详细解析
- It is evident that
 has only 2s and 3s in its prime factorization, or
has only 2s and 3s in its prime factorization, or  .
.
The LCM of any numbers an be found by writing out their factorizations and taking the greatest power for each factor.
![$[6^6,8^8] = 2^{24}3^6$](https://latex.artofproblemsolving.com/a/3/7/a3784d45cf90b4f699775de824f0cb19215f08f0.png) . Therefore
. Therefore ![$12^{12} = 2^{24}cdot3^{12} = [2^{24}3^6,2^a3^b] = 2^{max(24,a)}3^{max(6,b)}$](https://latex.artofproblemsolving.com/1/a/7/1a76da6ba7634a57a636d73a6428f2f9713b4c47.png) , and
, and  . Since
. Since  , there are
, there are  values of
values of  .
. - Pick's theorem states that:

The conditions give us four inequalities:
 ,
,  ,
,  ,
,  . These create a quadrilateral, whose area is
. These create a quadrilateral, whose area is  of the 30 by 30 square it is in. A simple way to see this is to note that the two triangles outside of the quadrilateral form half of the area of the 30 by 30 square.
of the 30 by 30 square it is in. A simple way to see this is to note that the two triangles outside of the quadrilateral form half of the area of the 30 by 30 square.So
 .
.  we can calculate by just counting. Ignoring the vertices, the top and right sides have 14 lattice points, and the two diagonals each have 14 lattice points (for the top diagonal, every value of
we can calculate by just counting. Ignoring the vertices, the top and right sides have 14 lattice points, and the two diagonals each have 14 lattice points (for the top diagonal, every value of  corresponds with an integer value of
corresponds with an integer value of  as
as  and vice versa for the bottom, so and there are 14 values for x not counting vertices). Adding the four vertices, there are 60 points on the borders.
and vice versa for the bottom, so and there are 14 values for x not counting vertices). Adding the four vertices, there are 60 points on the borders.

Since the inequalities also include the equals case, we include the boundaries, which gives us
 ordered pairs. However, the question asks us for positive integers, so
ordered pairs. However, the question asks us for positive integers, so  doesn't count; hence, the answer is
doesn't count; hence, the answer is  .
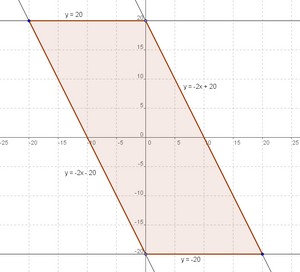
. - The equation given can be rewritten as:
We can split the equation into a piecewise equation by breaking up the absolute value:
Factoring the first one: (alternatively, it is also possible to complete the square)
Hence, either
 , or
, or  .
.Similarily, for the second one, we get
 or
or  . If we graph these four equations, we see that we get a parallelogram with base 20 and height 40. Hence the answer is
. If we graph these four equations, we see that we get a parallelogram with base 20 and height 40. Hence the answer is  .
.The equation can be rewritten as:
 . Do casework as above.
. Do casework as above. - In order for a player to have an odd sum, he must have an odd number of odd tiles: that is, he can either have three odd tiles, or two even tiles and an odd tile. Thus, since there are
 odd tiles and
odd tiles and  even tiles, the only possibility is that one player gets
even tiles, the only possibility is that one player gets  odd tiles and the other two players get
odd tiles and the other two players get  even tiles and
even tiles and  odd tile. We count the number of ways this can happen. (We will count assuming that it matters in what order the people pick the tiles; the final answer is the same if we assume the opposite, that order doesn't matter.)
odd tile. We count the number of ways this can happen. (We will count assuming that it matters in what order the people pick the tiles; the final answer is the same if we assume the opposite, that order doesn't matter.) choices for the tiles that he gets. The other two odd tiles can be distributed to the other two players in
choices for the tiles that he gets. The other two odd tiles can be distributed to the other two players in  ways, and the even tiles can be distributed between them in
ways, and the even tiles can be distributed between them in  ways. This gives us a total of
ways. This gives us a total of  possibilities in which all three people get odd sums.In order to calculate the probability, we need to know the total number of possible distributions for the tiles. The first player needs three tiles which we can give him in
possibilities in which all three people get odd sums.In order to calculate the probability, we need to know the total number of possible distributions for the tiles. The first player needs three tiles which we can give him in  ways, and the second player needs three of the remaining six, which we can give him in
ways, and the second player needs three of the remaining six, which we can give him in  ways. Finally, the third player will simply take the remaining tiles in
ways. Finally, the third player will simply take the remaining tiles in  way. So, there are
way. So, there are  ways total to distribute the tiles.We must multiply the probability by 3, since any of the 3 players can have the 3 odd tiles.Thus, the total probability is
ways total to distribute the tiles.We must multiply the probability by 3, since any of the 3 players can have the 3 odd tiles.Thus, the total probability is  so the answer is
so the answer is  .
. - Though the problem may appear to be quite daunting, it is actually not that difficult.
 always evaluates to an integer (triangular number), and the cosine of
always evaluates to an integer (triangular number), and the cosine of  where
where  is 1 if
is 1 if  is even and -1 if
is even and -1 if  is odd.
is odd.  will be even if
will be even if  or
or  , and odd otherwise.So our sum looks something like:
, and odd otherwise.So our sum looks something like: If we group the terms in pairs, we see that we need a formula for
If we group the terms in pairs, we see that we need a formula for  . So the first two fractions add up to
. So the first two fractions add up to  , the next two to
, the next two to  , and so forth.If we pair the terms again now, each pair adds up to
, and so forth.If we pair the terms again now, each pair adds up to  . There are
. There are  such pairs, so our answer is
such pairs, so our answer is 
-
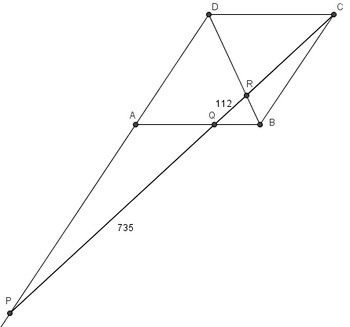
There are several similar triangles.
 , so we can write the proportion:
, so we can write the proportion:
Also,
 , so:
, so:

Substituting,



Thus,
 .
.We have
 so
so  . We also have
. We also have  so
so  . Equating the two results gives
. Equating the two results gives  and so
and so  which solves to
which solves to 
- Define
 . Then
. Then  , so
, so  .So we want to find four natural numbers that sum up to 51; we can imagine this as trying to split up 51 on the number line into 4 ranges. This is equivalent to trying to place 3 markers on the numbers 1 through 50; thus the answer is
.So we want to find four natural numbers that sum up to 51; we can imagine this as trying to split up 51 on the number line into 4 ranges. This is equivalent to trying to place 3 markers on the numbers 1 through 50; thus the answer is  , and
, and  .
. - The best way to start is to just write out some terms.
0 1 2 3 4 5 6  aa
aa aaa
aaa
 a
a


It is now apparent that each term can be written as
where the
 are Fibonacci numbers. This can be proven through induction.
are Fibonacci numbers. This can be proven through induction. - Let the two mathematicians be
 and
and  . Consider plotting the times that they are on break on a coordinate plane with one axis being the time
. Consider plotting the times that they are on break on a coordinate plane with one axis being the time  arrives and the second axis being the time
arrives and the second axis being the time  arrives (in minutes past 9 a.m.). The two mathematicians meet each other when
arrives (in minutes past 9 a.m.). The two mathematicians meet each other when  . Also because the mathematicians arrive between 9 and 10,
. Also because the mathematicians arrive between 9 and 10,  . Therefore,
. Therefore,  square represents the possible arrival times of the mathematicians, while the shaded region represents the arrival times where they meet.
square represents the possible arrival times of the mathematicians, while the shaded region represents the arrival times where they meet.![[asy] import graph; size(180); real m=60-12*sqrt(15); draw((0,0)--(60,0)--(60,60)--(0,60)--cycle); fill((m,0)--(60,60-m)--(60,60)--(60-m,60)--(0,m)--(0,0)--cycle,lightgray); draw((m,0)--(60,60-m)--(60,60)--(60-m,60)--(0,m)--(0,0)--cycle); xaxis("$M_1$",-10,80); yaxis("$M_2$",-10,80); label(rotate(45)*"$M_1-M_2le m$",((m+60)/2,(60-m)/2),NW,fontsize(9)); label(rotate(45)*"$M_1-M_2ge -m$",((60-m)/2,(m+60)/2),SE,fontsize(9)); label("$m$",(m,0),S); label("$m$",(0,m),W); label("$60$",(60,0),S); label("$60$",(0,60),W); [/asy]](https://latex.artofproblemsolving.com/6/6/e/66e5295ca62e55f572267d31580c6761602f96df.png) It's easier to compute the area of the unshaded region over the area of the total region, which is the probability that the mathematicians do not meet:
It's easier to compute the area of the unshaded region over the area of the total region, which is the probability that the mathematicians do not meet:




So the answer is
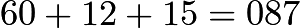 .
.Case 1:
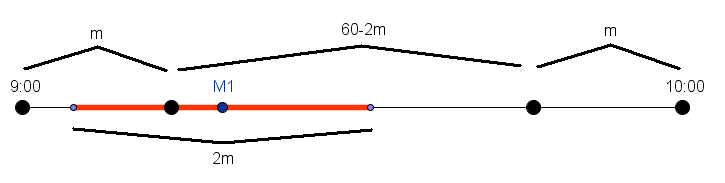 Case 2:
Case 2: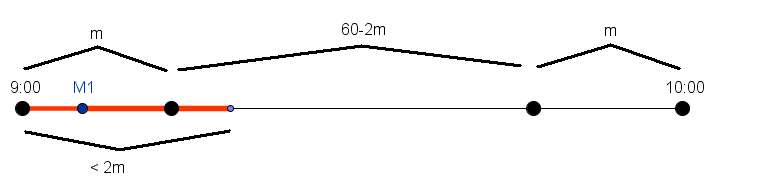
We draw a number line representing the time interval. If mathematician
 comes in at the center of the time period, then the two mathematicions will meet if
comes in at the center of the time period, then the two mathematicions will meet if  comes in somewhere between
comes in somewhere between  minutes before and after
minutes before and after  comes (a total range of
comes (a total range of 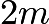 minutes). However, if
minutes). However, if  comes into the cafeteria in the first or last
comes into the cafeteria in the first or last  minutes, then the range in which
minutes, then the range in which  is reduced to somewhere in between
is reduced to somewhere in between  and
and 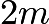 .
.We know try to find the weighted average of the chance that the two meet. In the central
 minutes,
minutes,  and
and  have to enter the cafeteria within
have to enter the cafeteria within  minutes of each other; so if we fix point
minutes of each other; so if we fix point  then
then  has a
has a  probability of meeting.
probability of meeting.In the first and last
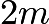 minutes, the probability that the two meet ranges from
minutes, the probability that the two meet ranges from  to
to  , depending upon the location of
, depending upon the location of  with respect to the endpoints. Intuitively, the average probability will occur at
with respect to the endpoints. Intuitively, the average probability will occur at 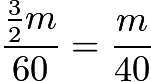 .
.So the weighted average is:
Solving this quadratic, we get two roots,
 . However,
. However,  , so we discard the greater root; and thus our answer
, so we discard the greater root; and thus our answer 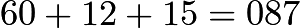 .
. - The key is to realize the significance that the figures are spheres, not circles. The 2D analogue of the diagram onto the flat surface will not contain 8 circles tangent to a ninth one; instead the circles will overlap since the middle sphere has a larger radius and will sort of “bulge” out.
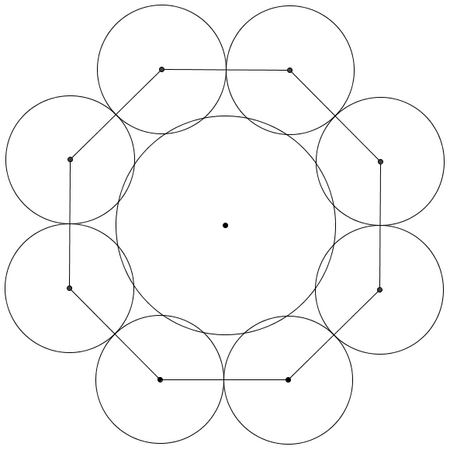 Let us examine the relation between one of the outside 8 spheres and the center one (with radius
Let us examine the relation between one of the outside 8 spheres and the center one (with radius  ):
):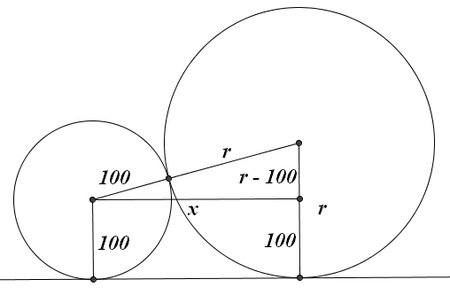 If we draw the segment containing the centers and the radii perpendicular to the flat surface, we get a trapezoid; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment
If we draw the segment containing the centers and the radii perpendicular to the flat surface, we get a trapezoid; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment  . Then by the Pythagorean Theorem:
. Then by the Pythagorean Theorem:![[x^2 + (r-100)^2 = (r+100)^2 Longrightarrow x = 20sqrt{r}]](https://latex.artofproblemsolving.com/0/8/e/08e7724efe90564b813ff6b7be1948902c6929ea.png)
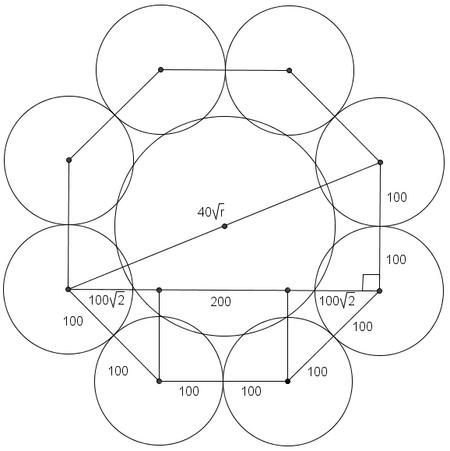
 is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length
is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length  . We can draw another right triangle as shown above. One leg has a length of
. We can draw another right triangle as shown above. One leg has a length of  . The other can be found by partitioning the leg into three sections and using
. The other can be found by partitioning the leg into three sections and using  s to see that the leg is
s to see that the leg is  . Pythagorean Theorem:
. Pythagorean Theorem:![begin{eqnarray*} (40sqrt{r})^2 &=& 200^2 + [200(sqrt{2}+1)]^2 1600r &=& 200^2[(1 + sqrt{2})^2 + 1] r &=& 100 + 50sqrt{2} end{eqnarray*}](https://latex.artofproblemsolving.com/7/6/f/76f1604de45c1a5d48c207c44614b154169ca381.png) Thus
Thus  .
. - This approach uses analytical geometry. Let
 be at the origin,
be at the origin,  at
at  ,
,  at
at  , and
, and  at
at  . Thus,
. Thus,  is at
is at  ,
,  is at
is at  , and
, and  is at
is at  .Let the plane
.Let the plane  have the equation
have the equation  . Using point
. Using point  , we get that
, we get that  . Using point
. Using point  , we get
, we get  . Using point
. Using point  , we get
, we get  . Thus plane
. Thus plane  ’s equation reduces to
’s equation reduces to  .We know need to find the intersection of this plane with that of
.We know need to find the intersection of this plane with that of  ,
,  ,
,  , and
, and  . After doing a little bit of algebra, the intersections are the lines
. After doing a little bit of algebra, the intersections are the lines  ,
,  ,
,  , and
, and  . Thus, there are three more vertices on the polygon, which are at
. Thus, there are three more vertices on the polygon, which are at  .We can find the lengths of the sides of the polygons now. There are 4 right triangles with legs of length 5 and 10, so their hypotenuses are
.We can find the lengths of the sides of the polygons now. There are 4 right triangles with legs of length 5 and 10, so their hypotenuses are  . The other two are of
. The other two are of  s with legs of length 15, so their hypotenuses are
s with legs of length 15, so their hypotenuses are  . So we have a hexagon with sides
. So we have a hexagon with sides  By symmetry, we know that opposite angles of the polygon are congruent. We can also calculate the length of the long diagonal by noting that it is of the same length of a face diagonal, making it
By symmetry, we know that opposite angles of the polygon are congruent. We can also calculate the length of the long diagonal by noting that it is of the same length of a face diagonal, making it  .
.![[asy] size(190); pointpen=black;pathpen=black; real s=2^.5; pair P=(0,0),Q=(7.5*s,2.5*s),R=Q+(0,15*s),Pa=(0,20*s),Qa=(-Q.x,Q.y),Ra=(-R.x,R.y); D(P--Q--R--Pa--Ra--Qa--cycle);D(R--Ra);D(Q--Qa);D(P--Pa); MP("15sqrt{2}",(Q+R)/2,E); MP("5sqrt{5}",(P+Q)/2,SE); MP("5sqrt{5}",(R+Pa)/2,NE); MP("20sqrt{2}",(P+Pa)/2,W); [/asy]](https://latex.artofproblemsolving.com/e/a/7/ea7bc05babcdcc882d8ac16161375c66d2551c11.png)
 . The Pythagorean Theorem gives that half of the base of the triangles is
. The Pythagorean Theorem gives that half of the base of the triangles is  . We find that the middle rectangle is actually a square, so the total area is
. We find that the middle rectangle is actually a square, so the total area is  .
. - We let
 ,
,  ,
,  . Since
. Since  and
and  ,
,  and
and  .By alternate interior angles, we have
.By alternate interior angles, we have  and
and  . By vertical angles,
. By vertical angles,  .Thus
.Thus  , so
, so  .Since
.Since  is equilateral,
is equilateral,  . Solving for
. Solving for  and
and  using
using  and
and  gives
gives  and
and  .Using the Law of Cosines, we get
.Using the Law of Cosines, we get

We want the ratio of the squares of the sides, so
 so
so  .
. - We note that the number of subsets (for now, including the empty subset, which we will just define to have a power sum of zero) with
 in it is equal to the number of subsets without a
in it is equal to the number of subsets without a  . To easily see this, take all possible subsets of
. To easily see this, take all possible subsets of  . Since the sets are ordered, a
. Since the sets are ordered, a  must go at the end; hence we can just append a
must go at the end; hence we can just append a  to any of those subsets to get a new one.Now that we have drawn that bijection, we can calculate the complex power sum recursively. Since appending a
to any of those subsets to get a new one.Now that we have drawn that bijection, we can calculate the complex power sum recursively. Since appending a  to a subset doesn't change anything about that subset's complex power sum besides adding an additional term, we have that
to a subset doesn't change anything about that subset's complex power sum besides adding an additional term, we have that  , where
, where  refers to the sum of all of the
refers to the sum of all of the  .It a subset of size 1 has a 9, then its power sum must be
.It a subset of size 1 has a 9, then its power sum must be  , and there is only
, and there is only  of these such subsets. There are
of these such subsets. There are  with
with  ,
,  with
with  , and so forth. So
, and so forth. So  . This is exactly the binomial expansion of
. This is exactly the binomial expansion of  . We can use De Moivre's Theorem to calculate the power:
. We can use De Moivre's Theorem to calculate the power:  . Hence
. Hence  , and
, and  . Thus,
. Thus,  .
. - Let’s solve for
 :
:![[(2mn)p = p(m+2)(n+2) + 2(m+2)(n+2)]](https://latex.artofproblemsolving.com/7/b/1/7b143cfbb2985678c4a7d6424e032e016fa2a879.png)
![[[2mn - (m+2)(n+2)]p = 2(m+2)(n+2)]](https://latex.artofproblemsolving.com/8/d/8/8d85d749a6a153c00912c02d1cc6bd841fb8f0f2.png)
![[p = frac{2(m+2)(n+2)}{mn - 2n - 2m - 4} = frac{2(m+2)(n+2)}{(m-2)(n-2) - 8}]](https://latex.artofproblemsolving.com/4/c/a/4ca431090d2a4c440e06936242d05d118a9b4789.png) Clearly, we want to minimize the denominator, so we test
Clearly, we want to minimize the denominator, so we test  . The possible pairs of factors of
. The possible pairs of factors of  are
are  . These give
. These give  and
and  respectively. Substituting into the numerator, we see that the first pair gives
respectively. Substituting into the numerator, we see that the first pair gives  , while the second pair gives
, while the second pair gives  . We now check that
. We now check that  is optimal, setting
is optimal, setting  ,
,  in order to simplify calculations. Since
in order to simplify calculations. Since![[0 le (a-1)(b-1) implies a+b le ab+1]](https://latex.artofproblemsolving.com/f/c/b/fcbb8bd5842ec9e3e12154c710e3221711c4ec51.png) We have
We have![[p = frac{2(a+4)(b+4)}{ab-8} = frac{2ab+8(a+b)+32}{ab-8} le frac{2ab+8(ab+1)+32}{ab-8} = 10 + frac{120}{ab-8} le 130]](https://latex.artofproblemsolving.com/b/4/b/b4b5f08e82b91dea4d2a91f26251aa9db9b5a164.png) Where we see
Where we see  gives us our maximum value of
gives us our maximum value of  .
.
- Note that
 assumes
assumes  , but this is clear as
, but this is clear as  and similarly for
and similarly for  .
.
- Note that
- We can draw a comparison between the domino a set of 40 points (labeled 1 through 40) in which every point is connected with every other point. The connections represent the dominoes.You need to have all even number of segments coming from each point except 0 or 2 which have an odd number of segments coming from the point. (Reasoning for this: Everytime you go to a vertex, you have to leave the vertex, so every vertex reached is equivalent to adding 2 more segments. So the degree of each vertex must be even, with the exception of endpoints) Since there are 39 segments coming from each point it is impossible to touch every segment.But you can get up to 38 on each segment because you go in to the point then out on a different segment. Counting going out from the starting and ending at the ending point we have:

以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1