- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
1999AIME 真题及答案解析
1999AIME 真题及答案解析
答案解析请参考文末
Problem 1
Find the smallest prime that is the fifth term of an increasing arithmetic sequence, all four preceding terms also being prime.
Problem 2
Consider the parallelogram with vertices ![]()
![]()
![]() and
and ![]() A line through the origin cuts this figure into two congruent polygons. The slope of the line is
A line through the origin cuts this figure into two congruent polygons. The slope of the line is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 3
Find the sum of all positive integers ![]() for which
for which ![]() is a perfect square.
is a perfect square.
Problem 4
The two squares shown share the same center ![]() and have sides of length 1. The length of
and have sides of length 1. The length of ![]() is
is ![]() and the area of octagon
and the area of octagon ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()

Problem 5
For any positive integer ![]() , let
, let ![]() be the sum of the digits of
be the sum of the digits of ![]() , and let
, and let ![]() be
be ![]() For example,
For example, ![]() How many values of
How many values of ![]() do not exceed 1999?
do not exceed 1999?
Problem 6
A transformation of the first quadrant of the coordinate plane maps each point ![]() to the point
to the point ![]() The vertices of quadrilateral
The vertices of quadrilateral ![]() are
are ![]() and
and ![]() Let
Let ![]() be the area of the region enclosed by the image of quadrilateral
be the area of the region enclosed by the image of quadrilateral ![]() Find the greatest integer that does not exceed
Find the greatest integer that does not exceed ![]()
Problem 7
There is a set of 1000 switches, each of which has four positions, called ![]() , and
, and ![]() . When the position of any switch changes, it is only from
. When the position of any switch changes, it is only from ![]() to
to ![]() , from
, from ![]() to
to ![]() , from
, from ![]() to
to ![]() , or from
, or from ![]() to
to ![]() . Initially each switch is in position
. Initially each switch is in position ![]() . The switches are labeled with the 1000 different integers
. The switches are labeled with the 1000 different integers ![]() , where
, where ![]() , and
, and ![]() take on the values
take on the values ![]() . At step
. At step ![]() of a 1000-step process, the
of a 1000-step process, the ![]() -th switch is advanced one step, and so are all the other switches whose labels divide the label on the
-th switch is advanced one step, and so are all the other switches whose labels divide the label on the ![]() -th switch. After step 1000 has been completed, how many switches will be in position
-th switch. After step 1000 has been completed, how many switches will be in position ![]() ?
?
Problem 8
Let ![]() be the set of ordered triples
be the set of ordered triples ![]() of nonnegative real numbers that lie in the plane
of nonnegative real numbers that lie in the plane ![]() Let us say that
Let us say that ![]() supports
supports ![]() when exactly two of the following are true:
when exactly two of the following are true: ![]() Let
Let ![]() consist of those triples in
consist of those triples in ![]() that support
that support ![]() The area of
The area of ![]() divided by the area of
divided by the area of ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()
Problem 9
A function ![]() is defined on the complex numbers by
is defined on the complex numbers by ![]() where
where ![]() and
and ![]() are positive numbers. This function has the property that the image of each point in the complex plane is equidistant from that point and the origin. Given that
are positive numbers. This function has the property that the image of each point in the complex plane is equidistant from that point and the origin. Given that ![]() and that
and that ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 10
Ten points in the plane are given, with no three collinear. Four distinct segments joining pairs of these points are chosen at random, all such segments being equally likely. The probability that some three of the segments form a triangle whose vertices are among the ten given points is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 11
Given that  where angles are measured in degrees, and
where angles are measured in degrees, and ![]() and
and ![]() are relatively prime positive integers that satisfy
are relatively prime positive integers that satisfy ![]() find
find ![]()
Problem 12
The inscribed circle of triangle ![]() is tangent to
is tangent to ![]() at
at ![]() and its radius is 21. Given that
and its radius is 21. Given that ![]() and
and ![]() find the perimeter of the triangle.
find the perimeter of the triangle.
Problem 13
Forty teams play a tournament in which every team plays every other(![]() different opponents) team exactly once. No ties occur, and each team has a
different opponents) team exactly once. No ties occur, and each team has a ![]() chance of winning any game it plays. The probability that no two teams win the same number of games is
chance of winning any game it plays. The probability that no two teams win the same number of games is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 14
Point ![]() is located inside triangle
is located inside triangle ![]() so that angles
so that angles ![]() and
and ![]() are all congruent. The sides of the triangle have lengths
are all congruent. The sides of the triangle have lengths ![]() and
and ![]() and the tangent of angle
and the tangent of angle ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 15
Consider the paper triangle whose vertices are ![]() and
and ![]() The vertices of its midpoint triangle are the midpoints of its sides. A triangular pyramid is formed by folding the triangle along the sides of its midpoint triangle. What is the volume of this pyramid?
The vertices of its midpoint triangle are the midpoints of its sides. A triangular pyramid is formed by folding the triangle along the sides of its midpoint triangle. What is the volume of this pyramid?
1999AIME 详细解析
- Obviously, all of the terms must be odd. The common difference between the terms cannot be
 or
or  , since otherwise there would be a number in the sequence that is divisible by
, since otherwise there would be a number in the sequence that is divisible by  . However, if the common difference is
. However, if the common difference is  , we find that
, we find that  , and
, and  form an arithmetic sequence. Thus, the answer is
form an arithmetic sequence. Thus, the answer is  .
. - Let the first point on the line
 be
be  where a is the height above
where a is the height above  . Let the second point on the line
. Let the second point on the line  be
be  . For two given points, the line will pass the origin if the coordinates are proportional (such that
. For two given points, the line will pass the origin if the coordinates are proportional (such that  ). Then, we can write that
). Then, we can write that  . Solving for
. Solving for  yields that
yields that  , so
, so  . The slope of the line (since it passes through the origin) is
. The slope of the line (since it passes through the origin) is  , and the solution is
, and the solution is  .
. - If
 for some positive integer
for some positive integer  , then rearranging we get
, then rearranging we get  . Now from the quadratic formula,
. Now from the quadratic formula,
Because
 is an integer, this means
is an integer, this means  for some nonnegative integer
for some nonnegative integer  . Rearranging gives
. Rearranging gives  . Thus
. Thus  or
or  , giving
, giving  or
or  . This gives
. This gives  or
or  , and the sum is
, and the sum is  .
.Suppose there is some
 such that
such that  . Completing the square, we have that
. Completing the square, we have that  , that is,
, that is,  . Multiplying both sides by 4 and rearranging, we see that
. Multiplying both sides by 4 and rearranging, we see that  . Thus,
. Thus,  . We then proceed as we did in the previous solution.
. We then proceed as we did in the previous solution. - Triangles
 ,
,  ,
,  , etc. are congruent by symmetry (you can prove it rigorously with congruent triangles), and each area is
, etc. are congruent by symmetry (you can prove it rigorously with congruent triangles), and each area is  . Since the area of a triangle is
. Since the area of a triangle is  , the area of all
, the area of all  of them is
of them is  and the answer is
and the answer is  .Define the two possible distances from one of the labeled points and the corners of the square upon which the point lies as
.Define the two possible distances from one of the labeled points and the corners of the square upon which the point lies as  and
and  . The area of the octagon (by subtraction of areas) is
. The area of the octagon (by subtraction of areas) is  .By the Pythagorean theorem,
.By the Pythagorean theorem,![[x^2 + y^2 = left(frac{43}{99}right)^2]](https://latex.artofproblemsolving.com/5/3/e/53e477338fc6a5946980845f2d103babe0c1b55e.png) Also,
Also, Substituting,
Substituting,
Thus, the area of the octagon is
 , so
, so  .]
.] - For most values of
 ,
,  will equal
will equal  . For those that don't, the difference must be bumping the number up a ten, a hundred, etc. If we take
. For those that don't, the difference must be bumping the number up a ten, a hundred, etc. If we take  as an example,
as an example,![[|(a + 1) + 0 + 0 + 1 - (a + 9 + 9 + 9)| = |2 - 9(3)|]](https://latex.artofproblemsolving.com/a/e/b/aeb23361465dcde0d545b66e70279e2ff9536f54.png) And in general, the values of
And in general, the values of  will then be in the form of
will then be in the form of  . From
. From  to
to  , there are
, there are  solutions; including
solutions; including  and there are a total of
and there are a total of  solutions.
solutions.  First we see that lines passing through
First we see that lines passing through  and
and  have equations
have equations  and
and  , respectively. Looking at the points above, we see the equations for
, respectively. Looking at the points above, we see the equations for  and
and  are
are  and
and  , or, after manipulation
, or, after manipulation  and
and  , respectively, which are still linear functions. Basically the square of the image points gives back the original points and we could plug them back into the original equation to get the equation of the image lines.Now take a look at
, respectively, which are still linear functions. Basically the square of the image points gives back the original points and we could plug them back into the original equation to get the equation of the image lines.Now take a look at  and
and  , which have the equations
, which have the equations  and
and  . The image equations hence are
. The image equations hence are  and
and  , respectively, which are the equations for circles.
, respectively, which are the equations for circles.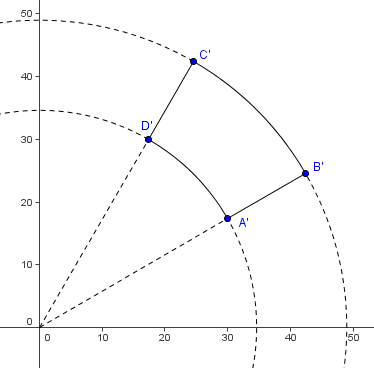 To find the area between the circles (actually, parts of the circles), we need to figure out the angle of the arc. This could be done by
To find the area between the circles (actually, parts of the circles), we need to figure out the angle of the arc. This could be done by  . So the requested areas are the area of the enclosed part of the smaller circle subtracted from the area enclosed by the part of the larger circle =
. So the requested areas are the area of the enclosed part of the smaller circle subtracted from the area enclosed by the part of the larger circle =  . Hence the answer is
. Hence the answer is  .
.- For each
 th switch (designated by
th switch (designated by  ), it advances itself only one time at the
), it advances itself only one time at the  th step; thereafter, only a switch with larger
th step; thereafter, only a switch with larger  values will advance the
values will advance the  th switch by one step provided
th switch by one step provided  divides
divides  . Let
. Let  be the max switch label. To find the divisor multiples in the range of
be the max switch label. To find the divisor multiples in the range of  to
to  , we consider the exponents of the number
, we consider the exponents of the number  . In general, the divisor-count of
. In general, the divisor-count of  must be a multiple of 4 to ensure that a switch is in position A:
must be a multiple of 4 to ensure that a switch is in position A:![$4n = [(9-x)+1] [(9-y)+1] [(9-z)+1] = (10-x)(10-y)(10-z)$](https://latex.artofproblemsolving.com/3/2/3/323a7b0ea0207ff505c100ebd4d9c498f2abdab0.png) , where
, where 
- Case of no 2's:
- The switches must be
 . There are
. There are  odd integers in
odd integers in  to
to  , so we have
, so we have  ways.
ways.
- Case of a single 2:
- The switches must be one of
 or
or  or
or  .
.
- Since
 the terms
the terms  and
and  are three valid choices for the
are three valid choices for the  factor above.
factor above.
- We have
 ways.
ways.
The number of switches in position A is
 .
. - This problem just requires a good diagram and strong 3D visualization.
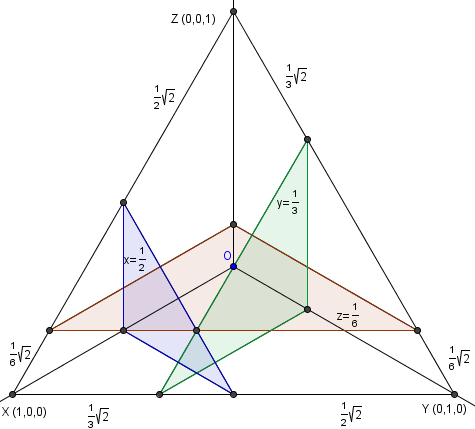 The region in
The region in  where
where  is that of a little triangle on the bottom of the above diagram, of
is that of a little triangle on the bottom of the above diagram, of  is the triangle at the right, and
is the triangle at the right, and  the triangle on the left, where the triangles are coplanar with the large equilateral triangle formed by
the triangle on the left, where the triangles are coplanar with the large equilateral triangle formed by  . We can check that each of the three regions mentioned fall under exactly two of the inequalities and not the third.
. We can check that each of the three regions mentioned fall under exactly two of the inequalities and not the third.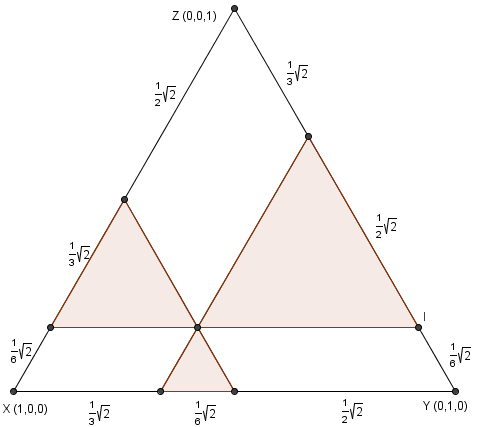 The side length of the large equilateral triangle is
The side length of the large equilateral triangle is  , which we can find using 45-45-90
, which we can find using 45-45-90  with the axes. Using the formula
with the axes. Using the formula  for equilateral triangles, the area of the large triangle is
for equilateral triangles, the area of the large triangle is  . Since the lines of the smaller triangles are parallel to those of the large triangle, by corresponding angles we see that all of the triangles are similar, so they are all equilateral triangles. We can solve for their side lengths easily by subtraction, and we get
. Since the lines of the smaller triangles are parallel to those of the large triangle, by corresponding angles we see that all of the triangles are similar, so they are all equilateral triangles. We can solve for their side lengths easily by subtraction, and we get  . Calculating their areas, we get
. Calculating their areas, we get  . The ratio
. The ratio  , and the answer is
, and the answer is  .
.
To simplify the problem, we could used the fact that the area ratios are equal to the side ratios squared, and we get
 .
. - Suppose we pick an arbitrary point on the complex plane, say
 . According to the definition of
. According to the definition of  ,
,![[f(1+i) = (a+bi)(1+i) = (a-b) + (a+b)i,]](https://latex.artofproblemsolving.com/c/1/9/c191c576a3df143ffdbd37f1c0b334bd2ac60d4e.png) this image must be equidistant to
this image must be equidistant to  and
and  . Thus the image must lie on the line with slope
. Thus the image must lie on the line with slope  and which passes through
and which passes through  , so its graph is
, so its graph is  . Substituting
. Substituting  and
and  , we get
, we get  .By the Pythagorean Theorem, we have
.By the Pythagorean Theorem, we have  , and the answer is
, and the answer is  .Plugging in
.Plugging in  yields
yields  . This implies that
. This implies that  must fall on the line
must fall on the line  , given the equidistant rule. By
, given the equidistant rule. By  , we get
, we get  , and plugging in
, and plugging in  yields
yields  . The answer is thus
. The answer is thus  .We are given that
.We are given that  is equidistant from the origin and
is equidistant from the origin and  This translates to
This translates to Since
Since 
 But
But  thus
thus  So the answer is
So the answer is  .
. - First, let us find the number of triangles that can be formed from the 10 points. Since none of the points are collinear, it is possible to pick
 sets of 3 points which form triangles. However, a fourth distinct segment must also be picked. Since the triangle accounts for 3 segments, there are
sets of 3 points which form triangles. However, a fourth distinct segment must also be picked. Since the triangle accounts for 3 segments, there are  segments remaining.The total number of ways of picking four distinct segments is
segments remaining.The total number of ways of picking four distinct segments is  . Thus, the requested probability is
. Thus, the requested probability is  . The solution is
. The solution is  .Note that 4 points can NEVER form 2 triangles. Therefore, we just need to multiply the probability that the first three segments picked form a triangle by 4. We can pick any segment for the first choice, then only segments that share an endpoint with the first one, then the one segment that completes the triangle. Note that the fourth segment doesn't matter in this case. Note that there are
.Note that 4 points can NEVER form 2 triangles. Therefore, we just need to multiply the probability that the first three segments picked form a triangle by 4. We can pick any segment for the first choice, then only segments that share an endpoint with the first one, then the one segment that completes the triangle. Note that the fourth segment doesn't matter in this case. Note that there are  segments that share an endpoint with the first segment. The answer is then
segments that share an endpoint with the first segment. The answer is then  -
- - Let
 . We could try to manipulate this sum by wrapping the terms around (since the first half is equal to the second half), but it quickly becomes apparent that this way is difficult to pull off. Instead, we look to telescope the sum. Using the identity
. We could try to manipulate this sum by wrapping the terms around (since the first half is equal to the second half), but it quickly becomes apparent that this way is difficult to pull off. Instead, we look to telescope the sum. Using the identity  , we can rewrite
, we can rewrite  as
as![[s cdot sin 5 = sum_{k=1}^{35} sin 5k sin 5 = sum_{k=1}^{35} frac{1}{2}(cos (5k - 5)- cos (5k + 5))]](https://latex.artofproblemsolving.com/c/4/a/c4af6b41beb9925f7cf087c3a087edb1db789ca5.png)
![[s = frac{0.5(cos 0 - cos 10 + cos 5 - cos 15 + cos 10 - cos 20 + ldots - cos 170 + cos 165 - cos 175+ cos 170 - cos 180)}{sin 5}]](https://latex.artofproblemsolving.com/f/6/3/f6392ba33a3da2657858b695d9bbc47978a3a0ed.png) This telescopes to
This telescopes to  . Manipulating this to use the identity
. Manipulating this to use the identity  , we get
, we get  , and our answer is
, and our answer is  .
. ![[asy] pathpen = black + linewidth(0.65); pointpen = black; pair A=(0,0),B=(50,0),C=IP(circle(A,23+245/2),circle(B,27+245/2)), I=incenter(A,B,C); path P = incircle(A,B,C); D(MP("A",A)--MP("B",B)--MP("C",C,N)--cycle);D(P); D(MP("P",IP(A--B,P))); pair Q=IP(C--A,P),R=IP(B--C,P); D(MP("R",R,NE));D(MP("Q",Q,NW)); MP("23",(A+Q)/2,W);MP("27",(B+R)/2,E); [/asy]](https://latex.artofproblemsolving.com/c/d/1/cd1d3a517ae3f4ddc9470481bb6e69b4808fbfaf.png)
 be the tangency point on
be the tangency point on  , and
, and  on
on  . By the Two Tangent Theorem,
. By the Two Tangent Theorem,  ,
,  , and
, and  . Using
. Using  , where
, where  , we get
, we get  . By Heron's formula,
. By Heron's formula,  . Equating and squaring both sides,
. Equating and squaring both sides,![begin{eqnarray*} [21(50+x)]^2 &=& (50+x)(x)(621)\ 441(50+x) &=& 621x\ 180x = 441 cdot 50 &Longrightarrow & x = frac{245}{2} end{eqnarray*}](https://latex.artofproblemsolving.com/3/8/4/384ebeab318f9bebe5275a899c6ed2423f1cb2f0.png) We want the perimeter, which is
We want the perimeter, which is  .Let the incenter be denoted
.Let the incenter be denoted  . It is commonly known that the incenter is the intersection of the angle bisectors of a triangle. So let
. It is commonly known that the incenter is the intersection of the angle bisectors of a triangle. So let  and
and  We have that
We have that So naturally we look at
So naturally we look at  But since
But since  we have
we have Doing the algebra, we get
Doing the algebra, we get 
The perimeter is therefore

- There are
 total pairings of teams, and thus
total pairings of teams, and thus  possible outcomes. In order for no two teams to win the same number of games, they must each win a different number of games. Since the minimum and maximum possible number of games won are 0 and 39 respectively, and there are 40 teams in total, each team corresponds uniquely with some
possible outcomes. In order for no two teams to win the same number of games, they must each win a different number of games. Since the minimum and maximum possible number of games won are 0 and 39 respectively, and there are 40 teams in total, each team corresponds uniquely with some  , with
, with  , where
, where  represents the number of games the team won. With this in mind, we see that there are a total of
represents the number of games the team won. With this in mind, we see that there are a total of  outcomes in which no two teams win the same number of games. Further, note that these are all the valid combinations, as the team with 1 win must beat the team with 0 wins, the team with 2 wins must beat the teams with 1 and 0 wins, and so on; thus, this uniquely defines a combination.The desired probability is thus
outcomes in which no two teams win the same number of games. Further, note that these are all the valid combinations, as the team with 1 win must beat the team with 0 wins, the team with 2 wins must beat the teams with 1 and 0 wins, and so on; thus, this uniquely defines a combination.The desired probability is thus  . We wish to simplify this into the form
. We wish to simplify this into the form  , where
, where  and
and  are relatively prime. The only necessary step is to factor out all the powers of 2 from
are relatively prime. The only necessary step is to factor out all the powers of 2 from  ; the remaining number is clearly relatively prime to all powers of 2.The number of powers of 2 in
; the remaining number is clearly relatively prime to all powers of 2.The number of powers of 2 in  is
is 
 .
. - Drop perpendiculars from
 to the three sides of
to the three sides of  and let them meet
and let them meet  and
and  at
at  and
and  respectively.
respectively.![[asy] import olympiad; real theta = 29.66115; /* arctan(168/295) to five decimal places .. don't know other ways to construct Brocard */ pathpen = black +linewidth(0.65); pointpen = black; pair A=(0,0),B=(13,0),C=IP(circle(A,15),circle(B,14)); D(MP("A",A)--MP("B",B)--MP("C",C,N)--cycle); /* constructing P, C is there as check */ pair Aa=A+(B-A)*dir(theta),Ba=B+(C-B)*dir(theta),Ca=C+(A-C)*dir(theta), P=IP(A--Aa,B--Ba); D(A--MP("P",P,SSW)--B);D(P--C); D(anglemark(B,A,P,30));D(anglemark(C,B,P,30));D(anglemark(A,C,P,30)); MP("13",(A+B)/2,S);MP("15",(A+C)/2,NW);MP("14",(C+B)/2,NE); /* constructing D,E,F as foot of perps from P */ pair D=foot(P,A,B),E=foot(P,B,C),F=foot(P,C,A); D(MP("D",D,NE)--P--MP("E",E,SSW),dashed);D(P--MP("F",F),dashed); D(rightanglemark(P,E,C,15));D(rightanglemark(P,F,C,15));D(rightanglemark(P,D,A,15)); [/asy]](https://latex.artofproblemsolving.com/f/b/1/fb1fb1dbb7c63477a671fab2b88af58222cc2d43.png)
 and
and  . We have that
. We have that We can then use the tool of calculating area in two ways
We can then use the tool of calculating area in two ways![begin{align*}[ABC]&=[PAB]+[PBC]+[PCA]\ &=frac{1}{2}(13)(ztantheta)+frac{1}{2}(14)(xtantheta)+frac{1}{2}(15)(ytantheta)\ &=frac{1}{2}tantheta(13z+14x+15y)end{align*}](https://latex.artofproblemsolving.com/2/c/1/2c13d0e92eb43d434482193a7cc53855f9b4a338.png) On the other hand,
On the other hand,![begin{align*}[ABC]&=sqrt{s(s-a)(s-b)(s-c)}\ &=sqrt{21cdot6cdot7cdot8}\ &=84end{align*}](https://latex.artofproblemsolving.com/c/6/e/c6e758ca750130a3e481d9d564db279ff9f4d00e.png) We still need
We still need  though. We have all these right triangles and we haven't even touched Pythagoras. So we give it a shot:
though. We have all these right triangles and we haven't even touched Pythagoras. So we give it a shot: Adding
Adding  gives
gives Recall that we found that
Recall that we found that ![$[ABC]=frac{1}{2}tantheta(13z+14x+15y)=84$](https://latex.artofproblemsolving.com/8/d/6/8d6c145cb2bf166cd4cd8339398205023b254869.png) . Plugging in
. Plugging in  , we get
, we get  , giving us
, giving us  for an answer.
for an answer. - Let
 ,
,  ,
,  be the feet of the altitudes to sides
be the feet of the altitudes to sides  ,
,  ,
,  , respectively, of
, respectively, of  . The base of the tetrahedron is the orthocenter
. The base of the tetrahedron is the orthocenter  of the large triangle, so we just need to find that, then it's easy from there. The reason why we find the orthocenter is due to the fact that once we fold the tetrahedron, finding the height requires perpendicular segments that are parallel to the large sides of the large triangle.To find the coordinates of
of the large triangle, so we just need to find that, then it's easy from there. The reason why we find the orthocenter is due to the fact that once we fold the tetrahedron, finding the height requires perpendicular segments that are parallel to the large sides of the large triangle.To find the coordinates of  , we need to find the intersection point of altitudes
, we need to find the intersection point of altitudes  and
and  . The equation of
. The equation of  is simply
is simply  .
.  is perpendicular to line
is perpendicular to line  , so the slope of
, so the slope of  is equal to the negative reciprocal of the slope of
is equal to the negative reciprocal of the slope of  .
.  has slope
has slope  , therefore
, therefore  . These two lines intersect at
. These two lines intersect at  , so that's the base of the height of the tetrahedron.Let
, so that's the base of the height of the tetrahedron.Let  be the foot of altitude
be the foot of altitude  in
in  . From the Pythagorean Theorem,
. From the Pythagorean Theorem,  . However, since
. However, since  and
and  are, by coincidence, the same point,
are, by coincidence, the same point,  and
and  .The area of the base is
.The area of the base is  , so the volume is
, so the volume is  .
.
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!
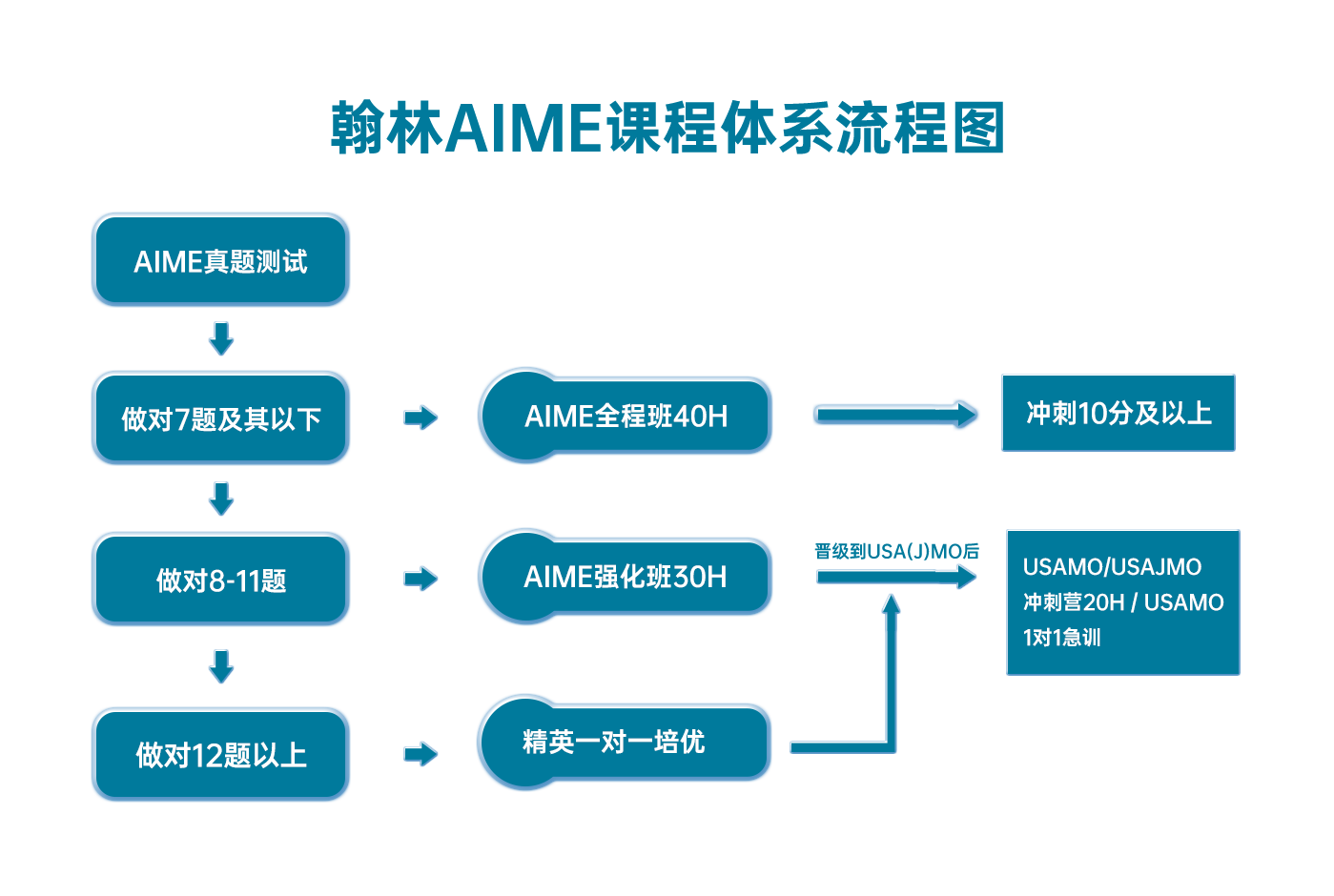
翰林AIME课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









