- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2000AIME I真题及答案解析
2000AIME I真题及答案解析
答案解析请参考文末
Problem 1
Find the least positive integer ![]() such that no matter how
such that no matter how ![]() is expressed as the product of any two positive integers, at least one of these two integers contains the digit
is expressed as the product of any two positive integers, at least one of these two integers contains the digit ![]() .
.
Problem 2
Let ![]() and
and ![]() be integers satisfying
be integers satisfying ![]() . Let
. Let ![]() , let
, let ![]() be the reflection of
be the reflection of ![]() across the line
across the line ![]() , let
, let ![]() be the reflection of
be the reflection of ![]() across the y-axis, let
across the y-axis, let ![]() be the reflection of
be the reflection of ![]() across the x-axis, and let
across the x-axis, and let ![]() be the reflection of
be the reflection of ![]() across the y-axis. The area of pentagon
across the y-axis. The area of pentagon ![]() is
is ![]() . Find
. Find ![]() .
.
Problem 3
In the expansion of ![]() where
where ![]() and
and ![]() are relatively prime positive integers, the coefficients of
are relatively prime positive integers, the coefficients of ![]() and
and ![]() are equal. Find
are equal. Find ![]() .
.
Problem 4
The diagram shows a rectangle that has been dissected into nine non-overlapping squares. Given that the width and the height of the rectangle are relatively prime positive integers, find the perimeter of the rectangle.
![[asy]draw((0,0)--(69,0)--(69,61)--(0,61)--(0,0));draw((36,0)--(36,36)--(0,36)); draw((36,33)--(69,33));draw((41,33)--(41,61));draw((25,36)--(25,61)); draw((34,36)--(34,45)--(25,45)); draw((34,45)--(41,45));[/asy]](https://latex.artofproblemsolving.com/1/0/f/10fdb489a934719f5e2fa8cfbc715a83c4e5648a.png)
Problem 5
Each of two boxes contains both black and white marbles, and the total number of marbles in the two boxes is ![]() One marble is taken out of each box randomly. The probability that both marbles are black is
One marble is taken out of each box randomly. The probability that both marbles are black is ![]() and the probability that both marbles are white is
and the probability that both marbles are white is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. What is
are relatively prime positive integers. What is ![]() ?
?
Problem 6
For how many ordered pairs ![]() of integers is it true that
of integers is it true that ![]() and that the arithmetic mean of
and that the arithmetic mean of ![]() and
and ![]() is exactly
is exactly ![]() more than the geometric mean of
more than the geometric mean of ![]() and
and ![]() ?
?
Problem 7
Suppose that ![]()
![]() and
and ![]() are three positive numbers that satisfy the equations
are three positive numbers that satisfy the equations ![]()
![]() and
and ![]() Then
Then ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 8
A container in the shape of a right circular cone is 12 inches tall and its base has a 5-inch radius. The liquid that is sealed inside is 9 inches deep when the cone is held with its point down and its base horizontal. When the liquid is held with its point up and its base horizontal, the height of the liquid is ![]() where
where ![]()
![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the cube of any prime number. Find
is not divisible by the cube of any prime number. Find ![]() .
.
Problem 9
The system of equations
has two solutions ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 10
A sequence of numbers ![]() has the property that, for every integer
has the property that, for every integer ![]() between
between ![]() and
and ![]() inclusive, the number
inclusive, the number ![]() is
is ![]() less than the sum of the other
less than the sum of the other ![]() numbers. Given that
numbers. Given that ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]() .
.
Problem 11
Let ![]() be the sum of all numbers of the form
be the sum of all numbers of the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive divisors of
are relatively prime positive divisors of ![]() What is the greatest integer that does not exceed
What is the greatest integer that does not exceed ![]() ?
?
Problem 12
Given a function ![]() for which
for which
Problem 13
In the middle of a vast prairie, a firetruck is stationed at the intersection of two perpendicular straight highways. The truck travels at ![]() miles per hour along the highways and at
miles per hour along the highways and at ![]() miles per hour across the prairie. Consider the set of points that can be reached by the firetruck within six minutes. The area of this region is
miles per hour across the prairie. Consider the set of points that can be reached by the firetruck within six minutes. The area of this region is ![]() square miles, where
square miles, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 14
In triangle ![]() it is given that angles
it is given that angles ![]() and
and ![]() are congruent. Points
are congruent. Points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() respectively, so that
respectively, so that ![]() Angle
Angle ![]() is
is ![]() times as large as angle
times as large as angle ![]() where
where ![]() is a positive real number. Find the greatest integer that does not exceed
is a positive real number. Find the greatest integer that does not exceed ![]() .
.
Problem 15
A stack of ![]() cards is labelled with the integers from
cards is labelled with the integers from ![]() to
to ![]() with different integers on different cards. The cards in the stack are not in numerical order. The top card is removed from the stack and placed on the table, and the next card is moved to the bottom of the stack. The new top card is removed from the stack and placed on the table, to the right of the card already there, and the next card in the stack is moved to the bottom of the stack. The process - placing the top card to the right of the cards already on the table and moving the next card in the stack to the bottom of the stack - is repeated until all cards are on the table. It is found that, reading from left to right, the labels on the cards are now in ascending order:
with different integers on different cards. The cards in the stack are not in numerical order. The top card is removed from the stack and placed on the table, and the next card is moved to the bottom of the stack. The new top card is removed from the stack and placed on the table, to the right of the card already there, and the next card in the stack is moved to the bottom of the stack. The process - placing the top card to the right of the cards already on the table and moving the next card in the stack to the bottom of the stack - is repeated until all cards are on the table. It is found that, reading from left to right, the labels on the cards are now in ascending order: ![]() In the original stack of cards, how many cards were above the card labeled
In the original stack of cards, how many cards were above the card labeled ![]() ?
?
2000AIME I详细解析
- If a factor of
 has a
has a  and a
and a  in its prime factorization, then that factor will end in a
in its prime factorization, then that factor will end in a  . Therefore, we have left to consider the case when the two factors have the
. Therefore, we have left to consider the case when the two factors have the  s and the
s and the  s separated, so we need to find the first power of 2 or 5 that contains a 0.For n = 1:
s separated, so we need to find the first power of 2 or 5 that contains a 0.For n = 1:![[2^1 = 2 , 5^1 = 5]](https://latex.artofproblemsolving.com/8/0/0/800db9e5191bc4e4a5a3b45161e9fb126ee24ca8.png) n = 2:
n = 2:![[2^2 = 4 , 5 ^ 2 =25]](https://latex.artofproblemsolving.com/3/5/b/35b9714a58da6c3e2555b8c22cf9c2d71234075f.png) n = 3:
n = 3:![[2^3 = 8 , 5 ^3 = 125]](https://latex.artofproblemsolving.com/b/9/b/b9b6c237c6b9f7c3394ebc7c9a2f05b3d34e07fe.png) and so on, until,n = 8:
and so on, until,n = 8: |
|  We see that
We see that  contains the first zero, so n =
contains the first zero, so n =  .
. ![[asy] pointpen = black; pathpen = linewidth(0.7) + black; size(180); pair A=(11,10), B=(10,11), C=(-10, 11), D=(-10, -11), E=(10, -11); D(D(MP("A (u,v)",A,(1,0)))--D(MP("B",B,N))--D(MP("C",C,N))--D(MP("D",D))--D(MP("E",E))--cycle); D((-15,0)--(15,0),linewidth(0.6),Arrows(5)); D((0,-15)--(0,15),linewidth(0.6),Arrows(5)); D((-15,-15)--(15,15),linewidth(0.6),Arrows(5)); [/asy]](https://latex.artofproblemsolving.com/d/4/9/d49b785d1030eea278bb89aaeeef04946478a11e.png)
 , we can find the coordinates of the other points:
, we can find the coordinates of the other points:  ,
,  ,
,  ,
,  . If we graph those points, we notice that since the latter four points are all reflected across the x/y-axis, they form a rectangle, and
. If we graph those points, we notice that since the latter four points are all reflected across the x/y-axis, they form a rectangle, and  is a triangle. The area of
is a triangle. The area of  is
is  and the area of
and the area of  is
is  . Adding these together, we get
. Adding these together, we get  . Since
. Since  are positive,
are positive,  , and by matching factors we get either
, and by matching factors we get either  or
or  . Since
. Since  the latter case is the answer, and
the latter case is the answer, and  .
.- Using the binomial theorem,
 .Since
.Since  and
and  are positive relatively prime integers,
are positive relatively prime integers,  and
and  , and
, and  .
. - Call the squares' side lengths from smallest to largest
 , and let
, and let  represent the dimensions of the rectangle.The picture shows that
represent the dimensions of the rectangle.The picture shows that Expressing all terms 3 to 9 in terms of
Expressing all terms 3 to 9 in terms of  and
and  and substituting their expanded forms into the previous equation will give the expression
and substituting their expanded forms into the previous equation will give the expression  .We can guess that
.We can guess that  . (If we started with
. (If we started with  odd, the resulting sides would not be integers and we would need to scale up by a factor of
odd, the resulting sides would not be integers and we would need to scale up by a factor of  to make them integers; if we started with
to make them integers; if we started with  even, the resulting dimensions would not be relatively prime and we would need to scale down.) Then solving gives
even, the resulting dimensions would not be relatively prime and we would need to scale down.) Then solving gives  ,
,  ,
,  , which gives us
, which gives us  . These numbers are relatively prime, as desired. The perimeter is
. These numbers are relatively prime, as desired. The perimeter is  .
. - If we work with the problem for a little bit, we quickly see that there is no direct combinatorics way to calculate
 . The Principle of Inclusion-Exclusion still requires us to find the individual probability of each box.Let
. The Principle of Inclusion-Exclusion still requires us to find the individual probability of each box.Let  represent the number of marbles in each box, and without loss of generality let
represent the number of marbles in each box, and without loss of generality let  . Then,
. Then,  , and since the
, and since the  may be reduced to form
may be reduced to form  on the denominator of
on the denominator of  ,
,  . It follows that
. It follows that  , so there are 2 pairs of
, so there are 2 pairs of  and
and  .
.
- Case 1: Then the product of the number of black marbles in each box is
 , so the only combination that works is
, so the only combination that works is  black in first box, and
black in first box, and  black in second. Then,
black in second. Then,  so
so  .
.
- Case 2: The only combination that works is 9 black in both. Thus,
 .
.  .
.
Thus,
 .
.Let
 and
and  represent the white and black marbles in boxes 1 and 2.
represent the white and black marbles in boxes 1 and 2.Since there are
 marbles in the box:
marbles in the box:
From the fact that there is a
 chance of drawing one black marble from each box:
chance of drawing one black marble from each box:
Thinking of the numerator and denominator separately, if
 was not a reduced fraction when calculating out the probability, then
was not a reduced fraction when calculating out the probability, then  . Since
. Since  , this forces the variables to be
, this forces the variables to be  and
and  in some permutation. Without loss of generality, let
in some permutation. Without loss of generality, let  and
and  .
.The denominator becomes:

Since there have been
 black marbles used, there must be
black marbles used, there must be  white marbles. Substituting that in:
white marbles. Substituting that in:

Since the factors of
 that are greater than
that are greater than  are
are  and
and  , the quantity
, the quantity  must equal one of those. However, since
must equal one of those. However, since  , testing
, testing  and
and  for
for  does not give a correct product. Thus,
does not give a correct product. Thus,  must be a reduced form of the actual fraction.
must be a reduced form of the actual fraction.First assume that the fraction was reduced from
 , yielding the equations
, yielding the equations  and
and  . Factoring
. Factoring  and saying WLOG that
and saying WLOG that  gives
gives  or
or  . Trying the first pair and setting the denominator equal to 100 gives:
. Trying the first pair and setting the denominator equal to 100 gives: 
Since
 , the pairs
, the pairs  and
and  can be tried, since each box must contain at least one white marble. Plugging in
can be tried, since each box must contain at least one white marble. Plugging in  gives the true equation
gives the true equation  , so the number of marbles are
, so the number of marbles are 
Thus, the chance of drawing 2 white marbles is
 in lowest terms, and the answer to the problem is
in lowest terms, and the answer to the problem is 
For completeness, the fraction
 may be tested.
may be tested.  is the highest necessary denominator that needs to be tested, since the maximum the denominator
is the highest necessary denominator that needs to be tested, since the maximum the denominator  can be when the sum of all integer variables is
can be when the sum of all integer variables is  is when the variables are
is when the variables are  and
and  , in some permutation, which gives
, in some permutation, which gives  . If
. If  , this forces
, this forces  , since all variables must be integers under
, since all variables must be integers under  . The denominator becomes
. The denominator becomes  , and since there are now
, and since there are now  white marbles total, the denominator becomes
white marbles total, the denominator becomes  . Testing
. Testing  gives a solution, and thus
gives a solution, and thus  . The complete solution for this case is
. The complete solution for this case is  . Although the distribution and colors of the marbles is different from the last case, the probability of drawing two white marbles is
. Although the distribution and colors of the marbles is different from the last case, the probability of drawing two white marbles is  , which still simplifies to
, which still simplifies to  .
. - Case 1: Then the product of the number of black marbles in each box is
 Because
Because  , we only consider
, we only consider  .For simplicity, we can count how many valid pairs of
.For simplicity, we can count how many valid pairs of  that satisfy our equation.The maximum that
that satisfy our equation.The maximum that  can be is
can be is  because
because  must be an integer (this is because
must be an integer (this is because  , an integer). Then
, an integer). Then  , and we continue this downward until
, and we continue this downward until  , in which case
, in which case  . The number of pairs of
. The number of pairs of  , and so
, and so  is then
is then  .
.- We can rewrite
 as
as  .Substituting into one of the given equations, we have
.Substituting into one of the given equations, we have![[x+xy=5]](https://latex.artofproblemsolving.com/d/d/3/dd3ecc078f3817630098087aee83b67949beba6f.png)
![[x(1+y)=5]](https://latex.artofproblemsolving.com/1/c/b/1cb3f4ba12300a2ba6fa50cfaf642fb3b737a683.png)
![[frac{1}{x}=frac{1+y}{5}.]](https://latex.artofproblemsolving.com/b/2/0/b20a007c0e51c72f671d05c32e59fba0e073bfdb.png) We can substitute back into
We can substitute back into  to obtain
to obtain![[y+frac{1+y}{5}=29]](https://latex.artofproblemsolving.com/d/3/2/d3295f9e9e6c592ff79d0a0bc270bd16bc98b4c4.png)
![[5y+1+y=145]](https://latex.artofproblemsolving.com/8/4/0/8408008569c2e0904634571649f36858844bb9f7.png)
![[y=24.]](https://latex.artofproblemsolving.com/5/e/b/5ebb1ed4f068b61be56ee31af56e6f64227e6027.png) We can then substitute once again to get
We can then substitute once again to get![[x=frac15]](https://latex.artofproblemsolving.com/9/0/0/900ce8fdd386c43652bbe5377b7770522eac3b00.png)
![[z=frac{5}{24}.]](https://latex.artofproblemsolving.com/d/3/a/d3a46c9b2ed835a4e51eedd24ff4abe32b38d57e.png) Thus,
Thus,  , so
, so  .
. - The scale factor is uniform in all dimensions, so the volume of the liquid is
 of the container. The remaining section of the volume is
of the container. The remaining section of the volume is  of the volume, and therefore
of the volume, and therefore  of the height when the vertex is at the top.So, the liquid occupies
of the height when the vertex is at the top.So, the liquid occupies  of the height, or
of the height, or  . Thus
. Thus  .(Computational) The volume of a cone can be found by
.(Computational) The volume of a cone can be found by  . In the second container, if we let
. In the second container, if we let  represent the height, radius (respectively) of the air (so
represent the height, radius (respectively) of the air (so  is the height of the liquid), then the volume of the liquid can be found by
is the height of the liquid), then the volume of the liquid can be found by  .By similar triangles, we find that the dimensions of the liquid in the first cone to the entire cone is
.By similar triangles, we find that the dimensions of the liquid in the first cone to the entire cone is  , and that
, and that  ; equating,
; equating,![begin{align*}frac{pi}{3}left(frac{3}{4}rright)^2 left(frac{3}{4}hright) &= frac{pi}{3}left(r^2h - left(frac{rh'}{h}right)^2h'right)\ frac{37}{64}r^2h &= frac{r^2}{h^2}(h')^3 \ h' &= sqrt[3]{frac{37}{64} cdot 12^3} = 3sqrt[3]{37}end{align*}](https://latex.artofproblemsolving.com/1/4/a/14ab28bada1a2faa03eb79845b8e1cef3c8a0d39.png)
Thus the answer is
![$12 - h' = 12-3sqrt[3]{37}$](https://latex.artofproblemsolving.com/9/c/e/9cefade80e75d0a63439935c0016c5ed094a047c.png) , and
, and  .
. - Since
 , we can reduce the equations to a more recognizable form:
, we can reduce the equations to a more recognizable form: Let
Let  be
be  respectively. Using SFFT, the above equations become (*)
respectively. Using SFFT, the above equations become (*) From here, multiplying the three equations gives
From here, multiplying the three equations gives

Dividing the third equation of (*) from this equation,
 . This gives
. This gives  , and the answer is
, and the answer is  .
. - Let the sum of all of the terms in the sequence be
 . Then for each integer
. Then for each integer  ,
,  . Summing this up for all
. Summing this up for all  from
from  ,
, Now, substituting for
Now, substituting for  , we get
, we get  , and the answer is
, and the answer is  .
. - Since all divisors of
 can be written in the form of
can be written in the form of  , it follows that
, it follows that  can also be expressed in the form of
can also be expressed in the form of  , where
, where  . Thus every number in the form of
. Thus every number in the form of  will be expressed one time in the product
will be expressed one time in the product![[(2^{-3} + 2^{-2} + 2^{-1} + 2^{0} + 2^{1} + 2^2 + 2^3)(5^{-3} + 5^{-2} +5^{-1} + 5^{0} + 5^{1} + 5^2 + 5^3)]](https://latex.artofproblemsolving.com/4/5/8/45856060696df39fc49e29ee269d2a07c63d853d.png) Using the formula for a geometric series, this reduces to
Using the formula for a geometric series, this reduces to  , and
, and  .
.  Since
Since  we can conclude that (by the Euclidean algorithm)
we can conclude that (by the Euclidean algorithm)![[f(x) = f(352 + x)]](https://latex.artofproblemsolving.com/6/e/9/6e9149a031c90a84a16859cc9886eeec06f9a836.png) So we need only to consider one period
So we need only to consider one period  , which can have at most
, which can have at most  distinct values which determine the value of
distinct values which determine the value of  at all other integers.But we also know that
at all other integers.But we also know that  , so the values
, so the values  and
and  are repeated. This gives a total of
are repeated. This gives a total of
![[352 - (46 - 24 + 1) - (351 - 200 + 1) = boxed{ 177 }]](https://latex.artofproblemsolving.com/6/2/e/62e798c9e5afa71ead09fa48297384cd4df01524.png)
distinct values.
To show that it is possible to have
 distinct, we try to find a function which fulfills the given conditions. A bit of trial and error would lead to the cosine function:
distinct, we try to find a function which fulfills the given conditions. A bit of trial and error would lead to the cosine function:  (in degrees).
(in degrees).- Let the intersection of the highways be at the origin
 , and let the highways be the x and y axes. We consider the case where the truck moves in the positive x direction.After going
, and let the highways be the x and y axes. We consider the case where the truck moves in the positive x direction.After going  miles,
miles,  hours has passed. If the truck leaves the highway it can travel for at most
hours has passed. If the truck leaves the highway it can travel for at most  hours, or
hours, or  miles. It can end up anywhere off the highway in a circle with this radius centered at
miles. It can end up anywhere off the highway in a circle with this radius centered at  . All these circles are homothetic with respect to a center at
. All these circles are homothetic with respect to a center at  .
.![[asy] pair truck(pair P){ pair Q = IP(P--P+(7/10,24/10),(35/31,35/31)--(5,0)); D(P--Q,EndArrow(5)); D(CP(P,Q),linewidth(0.5)); return Q; } pointpen = black; pathpen = black+linewidth(0.7); size(250); pair B=(5,0), C=(35/31,35/31); D(D(B)--D(C)--D(B*dir(90))--D(C*dir(90))--D(B*dir(180))--D(C*dir(180))--D(B*dir(270))--D(C*dir(270))--cycle); D((-6,0)--(6,0),Arrows(4)); D((0,-6)--(0,6),Arrows(4)); truck((1,0)); truck((2,0)); truck((3,0)); truck((4,0)); [/asy]](https://latex.artofproblemsolving.com/b/1/e/b1e4a60f3081861da720715755129e0abc341cb9.png)
![[asy] pointpen = black; pathpen = black+linewidth(0.7); size(250); pair O=(0,0), B=(5,0), A=1.4*expi(atan(24/7)), C=1.4*expi(atan(7/24)); D(D(B)--D(A)--D(O)); D(O--D(C)--D(B*dir(90))--D(A*dir(90))--O--D(C*dir(90))--D(B*dir(180))--D(A*dir(180))--O--D(C*dir(180))--D(B*dir(270))--D(A*dir(270))--O--D(C*dir(270))--B,linewidth(0.5)); D(CR(O,1.4)); D((-6,0)--(6,0),Arrows(4)); D((0,-6)--(0,6),Arrows(4)); MP("A",A,N); MP("B",B); MP("(5,0)",B,N); D(MP("left(frac{35}{31},frac{35}{31}right)",(35/31,35/31),NE)); D(rightanglemark(O,A,B)); [/asy]](https://latex.artofproblemsolving.com/b/1/d/b1dbbfe9154757443da1f35c5fce02513e7afdd6.png)
 . Draw a line tangent to it at
. Draw a line tangent to it at  and passing through
and passing through  . By the Pythagorean Theorem
. By the Pythagorean Theorem  . Then
. Then  , so the slope of line
, so the slope of line  is
is  . Since it passes through
. Since it passes through  its equation is
its equation is  .This line and the x and y axis bound the region the truck can go if it moves in the positive x direction. Similarly, the line
.This line and the x and y axis bound the region the truck can go if it moves in the positive x direction. Similarly, the line  bounds the region the truck can go if it moves in positive y direction. The intersection of these two lines is
bounds the region the truck can go if it moves in positive y direction. The intersection of these two lines is  . The bounded region in Quadrant I is made up of a square and two triangles.
. The bounded region in Quadrant I is made up of a square and two triangles.  . By symmetry, the regions in the other quadrants are the same, so the area of the whole region is
. By symmetry, the regions in the other quadrants are the same, so the area of the whole region is  so the answer is
so the answer is  .
. ![[asy]defaultpen(fontsize(8)); size(200); pair A=20*dir(80)+20*dir(60)+20*dir(100), B=(0,0), C=20*dir(0), P=20*dir(80)+20*dir(60), Q=20*dir(80), R=20*dir(60); draw(A--B--C--A);draw(P--Q);draw(A--R--B);draw(P--R);D(R--C,dashed); label("(A)",A,(0,1));label("(B)",B,(-1,-1));label("(C)",C,(1,-1));label("(P)",P,(1,1)); label("(Q)",Q,(-1,1));label("(R)",R,(1,0)); [/asy]](https://latex.artofproblemsolving.com/f/1/f/f1f597c511a21d50292f1daf4ee93815c1404c82.png)
 be in
be in  such that
such that  . Then
. Then  is a rhombus, so
is a rhombus, so  and
and  is an isosceles trapezoid. Since
is an isosceles trapezoid. Since  bisects
bisects  , it follows by symmetry in trapezoid
, it follows by symmetry in trapezoid  that
that  bisects
bisects  . Thus
. Thus  lies on the perpendicular bisector of
lies on the perpendicular bisector of  , and
, and  . Hence
. Hence  is an equilateral triangle.Now
is an equilateral triangle.Now  , and the sum of the angles in
, and the sum of the angles in  is
is  . Then
. Then  and
and  , so the answer is
, so the answer is  .
.- We try to work backwards from when there are 2 cards left, since this is when the 1999 card is laid onto the table. When there are 2 cards left, the 1999 card is on the top of the deck. In order for this to occur, it must be 2nd on the deck when there are 4 cards remaining, and this means it must be the 4th card when there are 8 cards remaining. This pattern continues until it is the 512th card on the deck when there are 1024 cards remaining. Since there are over 1000 cards remaining, some cards have not even made one trip through yet, 2(1024 - 1000) = 48, to be exact. Once these cards go through, 1999 will be the
 card on the deck. Since every other card was removed during the first round, it goes to show that 1999 was in position
card on the deck. Since every other card was removed during the first round, it goes to show that 1999 was in position  , meaning that there were
, meaning that there were  cards are above the one labeled
cards are above the one labeled  .
.
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!
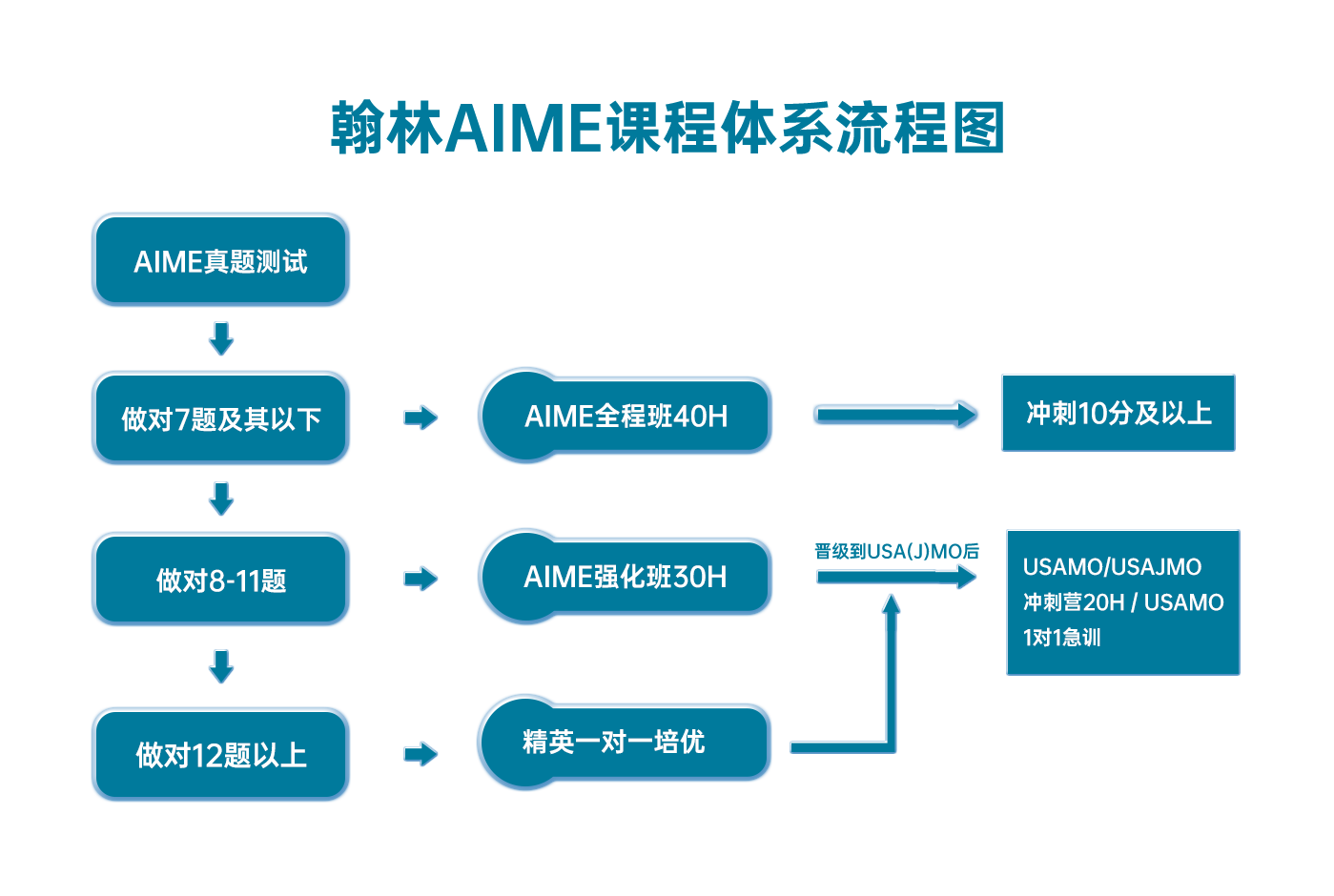
翰林AIME课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









