Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2002AIME II真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月11日下午5:36

2002AIME II真题及答案解析

答案解析请参考文末

Problem 1

Given that $x$ and $y$ are both integers between $100$ and $999$ , inclusive; $y$ is the number formed by reversing the digits of $x$ ; and $z=|x-y|$ . How many distinct values of $z$ are possible?

Problem 2

Three vertices of a cube are $P=(7,12,10)$ , $Q=(8,8,1)$ , and $R=(11,3,9)$ . What is the surface area of the cube?

Problem 3

It is given that $log_{6}a + log_{6}b + log_{6}c = 6$ , where $a$ , $b$ , and $c$ are positive integers that form an increasing geometric sequence and $b - a$ is the square of an integer. Find $a + b + c$ .

Problem 4

Patio blocks that are hexagons $1$ unit on a side are used to outline a garden by placing the blocks edge to edge with $n$ on each side. The diagram indicates the path of blocks around the garden when $n=5$ .

AIME 2002 II Problem 4.gif

If $n=202$ , then the area of the garden enclosed by the path, not including the path itself, is $mleft(sqrt3/2right)$ square units, where $m$ is a positive integer. Find the remainder when $m$ is divided by $1000$ .

Problem 5

Find the sum of all positive integers $a=2^n3^m$ where $n$ and $m$ are non-negative integers, for which $a^6$ is not a divisor of $6^a$ .

Problem 6

Find the integer that is closest to $1000sum_{n=3}^{10000}frac1{n^2-4}$ .

Problem 7

It is known that, for all positive integers $k$ ,

$1^2+2^2+3^2+ldots+k^{2}=frac{k(k+1)(2k+1)}6$ .Find the smallest positive integer $k$ such that $1^2+2^2+3^2+ldots+k^2$ is a multiple of $200$ .

Problem 8

Find the least positive integer $k$ for which the equation $leftlfloorfrac{2002}{n}rightrfloor=k$ has no integer solutions for $n$ . (The notation $lfloor xrfloor$ means the greatest integer less than or equal to $x$ .)

Problem 9

Let $mathcal{S}$ be the set $lbrace1,2,3,ldots,10rbrace$ Let $n$ be the number of sets of two non-empty disjoint subsets of $mathcal{S}$ . (Disjoint sets are defined as sets that have no common elements.) Find the remainder obtained when $n$ is divided by $1000$ .

Problem 10

While finding the sine of a certain angle, an absent-minded professor failed to notice that his calculator was not in the correct angular mode. He was lucky to get the right answer. The two least positive real values of $x$ for which the sine of $x$ degrees is the same as the sine of $x$ radians are $frac{mpi}{n-pi}$ and $frac{ppi}{q+pi}$ , where $m$ , $n$ , $p$ , and $q$ are positive integers. Find $m+n+p+q$ .

Problem 11

Two distinct, real, infinite geometric series each have a sum of $1$ and have the same second term. The third term of one of the series is $1/8$ , and the second term of both series can be written in the form $frac{sqrt{m}-n}p$ , where $m$ , $n$ , and $p$ are positive integers and $m$ is not divisible by the square of any prime. Find $100m+10n+p$ .

Problem 12

A basketball player has a constant probability of $.4$ of making any given shot, independent of previous shots. Let $a_n$ be the ratio of shots made to shots attempted after $n$ shots. The probability that $a_{10}=.4$ and $a_nle.4$ for all $n$ such that $1le nle9$ is given to be $p^aq^br/left(s^cright)$ where $p$ , $q$ , $r$ , and $s$ are primes, and $a$ , $b$ , and $c$ are positive integers. Find $left(p+q+r+sright)left(a+b+cright)$ .

Problem 13

In triangle $ABC$ , point $D$ is on $overline{BC}$ with $CD=2$ and $DB=5$ , point $E$ is on $overline{AC}$ with $CE=1$ and $EA=3$ , $AB=8$ , and $overline{AD}$ and $overline{BE}$ intersect at $P$ . Points $Q$ and $R$ lie on $overline{AB}$ so that $overline{PQ}$ is parallel to $overline{CA}$ and $overline{PR}$ is parallel to $overline{CB}$ . It is given that the ratio of the area of triangle $PQR$ to the area of triangle $ABC$ is $m/n$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .

Problem 14

The perimeter of triangle $APM$ is $152$ , and the angle $PAM$ is a right angle. A circle of radius $19$ with center $O$ on $overline{AP}$ is drawn so that it is tangent to $overline{AM}$ and $overline{PM}$ . Given that $OP=m/n$ where $m$ and $n$ are relatively prime positive integers, find $m+n$ .

Problem 15

Circles $mathcal{C}_{1}$ and $mathcal{C}_{2}$ intersect at two points, one of which is $(9,6)$ , and the product of the radii is $68$ . The x-axis and the line $y = mx$ , where $m > 0$ , are tangent to both circles. It is given that $m$ can be written in the form $asqrt {b}/c$ , where $a$ , $b$ , and $c$ are positive integers, $b$ is not divisible by the square of any prime, and $a$ and $c$ are relatively prime. Find $a + b + c$ .

2002AIME II详细解析

We express the numbers as $x=100a+10b+c$ and $y=100c+10b+a$ . From this, we have $begin{eqnarray*}z&=&|100a+10b+c-100c-10b-a|&=&|99a-99c|&=&99|a-c| end{eqnarray*}$ Because $a$ and $c$ are digits, and $a$ and $c$ are both between 1 and 9 (from condition 1), there are $boxed{009}$ possible values (since all digits except $9$ can be expressed this way).
$PQ=sqrt{(8-7)^2+(8-12)^2+(1-10)^2}=sqrt{98}$ $PR=sqrt{(11-7)^2+(3-12)^2+(9-10)^2}=sqrt{98}$ $QR=sqrt{(11-8)^2+(3-8)^2+(9-1)^2}=sqrt{98}$ So, $PQR$ is an equilateral triangle. Let the side of the cube be $a$ . $asqrt{2}=sqrt{98}$
So, $a=7$ , and hence the surface area is $6a^2=framebox{294}$ .
$abc=6^6$ . Since they form an increasing geometric sequence, $b$ is the geometric mean of the product $abc$ . $b=sqrt[3]{abc}=6^2=36$ .Since $b-a$ is the square of an integer, we can find a few values of $a$ that work: $11, 20, 27, 32,$ and $35$ . Out of these, the only value of $a$ that works is $a=27$ , from which we can deduce that $c=dfrac{36}{27}cdot 36=dfrac{4}{3}cdot 36=48$ .Thus, $a+b+c=27+36+48=boxed{111}$
When $n>1$ , the path of blocks has $6(n-1)$ blocks total in it. When $n=1$ , there is just one lonely block. Thus, the area of the garden enclosed by the path when $n=202$ is $[(1+6+12+18+cdots +1200)A=(1+6(1+2+3...+200))A]$ ,where $A$ is the area of one block. Then, because $n(n+1)/2$ is equal to the sum of the first $n$ integers: $[(1+6(1+2+3...+200))=(1+6((200)(201)/2))A=120601A]$ .Since $A=dfrac{3sqrt{3}}{2}$ , the area of the garden is
$[120601cdot dfrac{3sqrt{3}}{2}=dfrac{361803sqrt{3}}{2}]$ .

$m=361803$ , $dfrac{m}{1000}=361$ Remainder $boxed{803}$ .
Substitute $a=2^n3^m$ into $a^6$ and $6^a$ , and find all pairs of non-negative integers (n,m) for which $(2^n3^m)^{6}$ is not a divisor of $6^{2^n3^m}$ Simplifying both expressions: $2^{6n} cdot 3^{6m}$ is not a divisor of $2^{2^n3^m} cdot 3^{2^n3^m}$ Comparing both exponents (noting that there must be either extra powers of 2 or extra powers of 3 in the left expression): $6n > 2^n3^m$ OR $6m > 2^n3^m$
Using the first inequality $6n > 2^n3^m$ and going case by case starting with n $in$ {0, 1, 2, 3...}:

n=0: $0>1 cdot 3^m$ which has no solution for non-negative integers m

n=1: $6 > 2 cdot 3^m$ which is true for m=0 but fails for higher integers $Rightarrow (1,0)$

n=2: $12 > 4 cdot 3^m$ which is true for m=0 but fails for higher integers $Rightarrow (2,0)$

n=3: $18 > 8 cdot 3^m$ which is true for m=0 but fails for higher integers $Rightarrow (3,0)$

n=4: $24 > 16 cdot 3^m$ which is true for m=0 but fails for higher integers $Rightarrow (4,0)$

n=5: $30 > 32 cdot 3^m$ which has no solution for non-negative integers m

There are no more solutions for higher $n$ , as polynomials like $6n$ grow slower than exponentials like $2^n$ .

Using the second inequality $6m > 2^n3^m$ and going case by case starting with m $in$ {0, 1, 2, 3...}:

m=0: $0>2^n cdot 1$ which has no solution for non-negative integers n

m=1: $6>2^n cdot 3$ which is true for n=0 but fails for higher integers $Rightarrow (0,1)$

m=2: $12>2^n cdot 9$ which is true for n=0 but fails for higher integers $Rightarrow (0,2)$

m=3: $18>2^n cdot 27$ which has no solution for non-negative integers n

There are no more solutions for higher $m$ , as polynomials like $6m$ grow slower than exponentials like $3^m$ .

Thus there are six numbers corresponding to (1,0), (2,0), (3,0), (4,0), (0,1), and (0,2). Plugging them back into the original expression, these numbers are 2, 4, 8, 16, 3, and 9, respectively. Their sum is $framebox{42}$ .
We know that $frac{4}{n^2 - 4} = frac{1}{n-2} - frac{1}{n + 2}$ .So if we pull the $frac{1}{4}$ out of the summation, you get $250sum_{n=3}^{10,000} (frac{1}{n-2} - frac{1}{n + 2})$ .Now that telescopes, leaving you with: $250 (1 + frac{1}{2} + frac{1}{3} + frac{1}{4} - frac{1}{9999} - frac{1}{10000} - frac{1}{10001} - frac{1}{10002}) = 250 + 125 + 83.3 + 62.5 - 250 (- frac{1}{9999} - frac{1}{10000} - frac{1}{10001} - frac{1}{10002})$
The small fractional terms are not enough to bring $520.8$ lower than $520.5,$ so the answer is $fbox{521}$

If you didn't know $frac{4}{n^2 - 4} = frac{1}{n-2} - frac{1}{n + 2}$ , here's how you can find it out:

We know $frac{1}{n^2 - 4} = frac{1}{(n+2)(n-2)}$ . We can use the process of fractional decomposition to split this into two fractions thus: $frac{1}{(n+2)(n-2)} = frac{A}{(n+2)} + frac{B}{(n-2)}$ for some A and B.

Solving for A and B gives $1 = (n-2)A + (n+2)B$ or $1 = n(A+B)+ 2(B-A)$ . Since there is no n term on the left hand side, $A+B=0$ and by inspection $1 = 2(B-A)$ . Solving yields $A=frac{1}{4}, B=frac{-1}{4}$

Then we have $frac{1}{(n+2)(n-2)} = frac{ frac{1}{4} }{(n-2)} + frac{ frac{-1}{4} }{(n+2)}$ and we can continue as before.
$frac{k(k+1)(2k+1)}{6}$ is a multiple of $200$ if $k(k+1)(2k+1)$ is a multiple of $1200 = 2^4 cdot 3 cdot 5^2$ . So $16,3,25|k(k+1)(2k+1)$ .Since $2k+1$ is always odd, and only one of $k$ and $k+1$ is even, either $k, k+1 equiv 0 pmod{16}$ .Thus, $k equiv 0, 15 pmod{16}$ .If $k equiv 0 pmod{3}$ , then $3|k$ . If $k equiv 1 pmod{3}$ , then $3|2k+1$ . If $k equiv 2 pmod{3}$ , then $3|k+1$ .Thus, there are no restrictions on $k$ in $pmod{3}$ .
It is easy to see that only one of $k$ , $k+1$ , and $2k+1$ is divisible by $5$ . So either $k, k+1, 2k+1 equiv 0 pmod{25}$ .

Thus, $k equiv 0, 24, 12 pmod{25}$ .

From the Chinese Remainder Theorem, $k equiv 0, 112, 224, 175, 287, 399 pmod{400}$ . Thus, the smallest positive integer $k$ is $boxed{112}$ .
Note that if $frac{2002}n - frac{2002}{n+1}leq 1$ , then either $leftlfloorfrac{2002}{n}rightrfloor=leftlfloorfrac{2002}{n+1}rightrfloor$ , or $leftlfloorfrac{2002}{n}rightrfloor=leftlfloorfrac{2002}{n+1}rightrfloor+1$ . Either way, we won't skip any natural numbers.The greatest $n$ such that $frac{2002}n - frac{2002}{n+1} > 1$ is $n=44$ . (The inequality simplifies to $n(n+1)<2002$ , which is easy to solve by trial, as the solution is obviously $simeq sqrt{2002}$ .)We can now compute: $[leftlfloorfrac{2002}{45}rightrfloor=44]$ $[leftlfloorfrac{2002}{44}rightrfloor=45]$ $[leftlfloorfrac{2002}{43}rightrfloor=46]$ $[leftlfloorfrac{2002}{42}rightrfloor=47]$ $[leftlfloorfrac{2002}{41}rightrfloor=48]$ $[leftlfloorfrac{2002}{40}rightrfloor=50]$ From the observation above (and the fact that $leftlfloorfrac{2002}{2002}rightrfloor=1$ ) we know that all integers between $1$ and $44$ will be achieved for some values of $n$ . Similarly, for $n<40$ we obviously have $leftlfloorfrac{2002}{n}rightrfloor > 50$ .Hence the least positive integer $k$ for which the equation $leftlfloorfrac{2002}{n}rightrfloor=k$ has no integer solutions for $n$ is $boxed{049}$ .
Let the two disjoint subsets be $A$ and $B$ , and let $C = S-(A+B)$ . For each $i in S$ , either $i in A$ , $i in B$ , or $i in C$ . So there are $3^{10}$ ways to organize the elements of $S$ into disjoint $A$ , $B$ , and $C$ .However, there are $2^{10}$ ways to organize the elements of $S$ such that $A = emptyset$ and $S = B+C$ , and there are $2^{10}$ ways to organize the elements of $S$ such that $B = emptyset$ and $S = A+C$ . But, the combination such that $A = B = emptyset$ and $S = C$ is counted twice.Thus, there are $3^{10}-2cdot2^{10}+1$ ordered pairs of sets $(A,B)$ . But since the question asks for the number of unordered sets ${ A,B }$ , $n = frac{1}{2}(3^{10}-2cdot2^{10}+1) = 28501 equiv boxed{501} pmod{1000}$ .
Note that $x$ degrees is equal to $frac{pi x}{180}$ radians. Also, for $alpha in left[0 , frac{pi}{2} right]$ , the two least positive angles $theta > alpha$ such that $sin{theta} = sin{alpha}$ are $theta = pi-alpha$ , and $theta = 2pi + alpha$ .Clearly $x > frac{pi x}{180}$ for positive real values of $x$ . $theta = pi-alpha$ yields: $x = pi - frac{pi x}{180} Rightarrow x = frac{180pi}{180+pi} Rightarrow (p,q) = (180,180)$ . $theta = 2pi + alpha$ yields: $x = 2pi + frac{pi x}{180} Rightarrow x = frac{360pi}{180-pi} Rightarrow (m,n) = (360,180)$ .So, $m+n+p+q = boxed{900}$ .
Let the second term of each series be $x$ . Then, the common ratio is $frac{1}{8x}$ , and the first term is $8x^2$ .So, the sum is $frac{8x^2}{1-frac{1}{8x}}=1$ . Thus, $64x^3-8x+1 = (4x-1)(16x^2+4x-1) = 0 Rightarrow x = frac{1}{4}, frac{-1 pm sqrt{5}}{8}$ .The only solution in the appropriate form is $x = frac{sqrt{5}-1}{8}$ . Therefore, $100m+10n+p = boxed{518}$ .
The first restriction is that $a_{10} = .4$ , meaning that the player gets exactly 4 out of 10 baskets. The second restriction is $a_nle.4$ . This means that the player may never have a shooting average over 40%. Thus, the first and second shots must fail, since $frac{1}{1}$ and $frac{1}{2}$ are both over $.4$ , but the player may make the third basket, since $frac{1}{3} le .4$ In other words, the earliest the first basket may be made is attempt 3. Using similar reasoning, the earliest the second basket may be made is attempt 5, the earliest the third basket may be made is attempt 8, and the earliest the fourth basket may be made is attempt 10.Using X to represent a basket and O to represent a failure, this 'earliest' solution may be represented as:OOXOXOOXOXTo simplify counting, note that the first, second, and tenth shots are predetermined. The first two shots must fail, and the last shot must succeed. Thus, only slots 3-9 need to be counted, and can be abbreviated as follows:XOXOOXO
The problem may be separated into five cases, since the first shot may be made on attempt 3, 4, 5, 6, or 7. The easiest way to count the problem is to remember that each X may slide to the right, but NOT to the left.

First shot made on attempt 3:

XOXOOXO

XOXOOOX

XOOXOXO

XOOXOOX

XOOOXXO

XOOOXOX

XOOOOXX

Total - 7

First shot made on attempt 4:

Note that all that needs to be done is change each line in the prior case from starting with "XO....." to "OX.....".

Total - 7

First shot made on attempt 5:

OOXXOXO

OOXXOOX

OOXOXXO

OOXOXOX

OOXOOXX

Total - 5

First shot made on attempt 6:

OOOXXXO

OOOXXOX

OOOXOXX

Total - 3

First shot made on attempt 7:

OOOOXXX

Total - 1

The total number of ways the player may satisfy the requirements is $7+7+5+3+1=23$ .

The chance of hitting any individual combination (say, for example, OOOOOOXXXX) is $left(frac{3}{5}right)^6left(frac{2}{5}right)^4$

Thus, the chance of hitting any of these 23 combinations is $23left(frac{3}{5}right)^6left(frac{2}{5}right)^4 = frac{23cdot3^6cdot2^4}{5^{10}}$

Thus, the final answer is $(23+3+2+5)(6+4+10)=boxed{660}$
Let $X$ be the intersection of $overline{CP}$ and $overline{AB}$ . $[asy] size(10cm); pair A,B,C,D,E,X,P,Q,R; A=(0,0); B=(8,0); C=(1.9375,3.4994); D=(3.6696,2.4996); E=(1.4531,2.6246); X=(4.3636,0); P=(2.9639,2.0189); Q=(1.8462,0); R=(6.4615,0); dot(A); dot(B); dot(C); dot(D); dot(E); dot(X); dot(P); dot(Q); dot(R); label("$A$",A,WSW); label("$B$",B,ESE); label("$C$",C,NNW); label("$D$",D,NE); label("$E$",E,WNW); label("$X$",X,SSE); label("$P$",P,NNE); label("$Q$",Q,SSW); label("$R$",R,SE); draw(A--B--C--cycle); draw(P--Q--R--cycle); draw(A--D); draw(B--E); draw(C--X); [/asy]$ Since $overline{PQ} parallel overline{CA}$ and $overline{PR} parallel overline{CB}$ , $angle CAB = angle PQR$ and $angle CBA = angle PRQ$ . So $Delta ABC sim Delta QRP$ , and thus, $frac{[Delta PQR]}{[Delta ABC]} = left(frac{PX}{CX}right)^2$ .Using mass points:WLOG, let $W_C=15$ .
Then:

$W_A = left(frac{CE}{AE}right)W_C = frac{1}{3}cdot15=5$ .

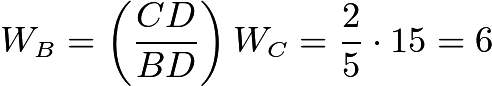$W_B = left(frac{CD}{BD}right)W_C = frac{2}{5}cdot15=6$ .

$W_X=W_A+W_B=5+6=11$ .

$W_P=W_C+W_X=15+11=26$ .

Thus, $frac{PX}{CX}=frac{W_C}{W_P}=frac{15}{26}$ . Therefore, $frac{[Delta PQR]}{[Delta ABC]} = left( frac{15}{26} right)^2 = frac{225}{676}$ , and $m+n=boxed{901}$ .
Let the circle intersect $overline{PM}$ at $B$ . Then note $triangle OPB$ and $triangle MPA$ are similar. Also note that $AM = BM$ by power of a point. So we have $[frac{19}{AM} = frac{152-2AM}{152}]$ Solving, $AM = 38$ . So the ratio of the side lengths of the triangles is 2. Therefore, $[frac{PB+38}{OP}= 2 text{ and } frac{OP+19}{PB} = 2]$ so $2OP = PB+38$ and $2PB = OP+19.$ Substituting for $PB$ , we see that $4OP-76 = OP+19$ , so $OP = frac{95}3$ and the answer is $boxed{098}$ .
Let the smaller angle between the $x$ -axis and the line $y=mx$ be $theta$ . Note that the centers of the two circles lie on the angle bisector of the angle between the $x$ -axis and the line $y=mx$ . Also note that if $(x,y)$ is on said angle bisector, we have that $frac{y}{x}=tan{frac{theta}{2}}$ . Let $tan{frac{theta}{2}}=m_1$ , for convenience. Therefore if $(x,y)$ is on the angle bisector, then $x=frac{y}{m_1}$ . Now let the centers of the two relevant circles be $(a/m_1 , a)$ and $(b/m_1 , b)$ for some positive reals $a$ and $b$ . These two circles are tangent to the $x$ -axis, so the radii of the circles are $a$ and $b$ respectively. We know that the point $(9,6)$ is a point on both circles, so we have that $[(9-frac{a}{m_1})^2+(6-a)^2=a^2]$ $[(9-frac{b}{m_1})^2+(6-b)^2=b^2]$ Expanding these and manipulating terms gives $[frac{1}{m_1^2}a^2-[(18/m_1)+12]a+117=0]$
$[frac{1}{m_1^2}b^2-[(18/m_1)+12]b+117=0]$

It follows that $a$ and $b$ are the roots of the quadratic

$[frac{1}{m_1^2}x^2-[(18/m_1)+12]x+117=0]$

It follows from Vieta's Formulas that the product of the roots of this quadratic is $117m_1^2$ , but we were also given that the product of the radii was 68. Therefore $68=117m_1^2$ , or $m_1^2=frac{68}{117}$ . Note that the half-angle formula for tangents is

$[tan{frac{theta}{2}}=sqrt{frac{1-cos{theta}}{1+cos{theta}}}]$

Therefore

$[frac{68}{117}=frac{1-cos{theta}}{1+cos{theta}}]$

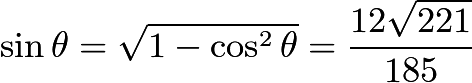Solving for $cos{theta}$ gives that $cos{theta}=frac{49}{185}$ . It then follows that $sin{theta}=sqrt{1-cos^2{theta}}=frac{12sqrt{221}}{185}$ .

It then follows that $m=tan{theta}=frac{12sqrt{221}}{49}$ . Therefore $a=12$ , $b=221$ , and $c=49$ . The desired answer is then $12+221+49=boxed{282}$ .