Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2006AIME II真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月9日下午5:04

2006AIME II真题及答案解析

答案解析请参考文末

Problem 1

In convex hexagon $ABCDEF$ , all six sides are congruent, $angle A$ and $angle D$ are right angles, and $angle B, angle C, angle E,$ and $angle F$ are congruent. The area of the hexagonal region is $2116(sqrt{2}+1).$ Find $AB$ .

Problem 2

The lengths of the sides of a triangle with positive area are $log_{10} 12$ , $log_{10} 75$ , and $log_{10} n$ , where $n$ is a positive integer. Find the number of possible values for $n$ .

Problem 3

Let $P$ be the product of the first 100 positive odd integers. Find the largest integer $k$ such that $P$ is divisible by $3^k$ .

Problem 4

Let $(a_1,a_2,a_3,ldots,a_{12})$ be a permutation of $(1,2,3,ldots,12)$ for which

$a_1>a_2>a_3>a_4>a_5>a_6 mathrm{ and } a_6<a_7<a_8<a_9<a_{10}<a_{11}<a_{12}.$ An example of such a permutation is $(6,5,4,3,2,1,7,8,9,10,11,12).$ Find the number of such permutations.

Problem 5

When rolling a certain unfair six-sided die with faces numbered 1, 2, 3, 4, 5, and 6, the probability of obtaining face $F$ is greater than 1/6, the probability of obtaining the face opposite is less than 1/6, the probability of obtaining any one of the other four faces is 1/6, and the sum of the numbers on opposite faces is 7. When two such dice are rolled, the probability of obtaining a sum of 7 is 47/288. Given that the probability of obtaining face $F$ is $m/n,$ where $m$ and $n$ are relatively prime positive integers, find $m+n.$

Problem 6

Square $ABCD$ has sides of length 1. Points $E$ and $F$ are on $overline{BC}$ and $overline{CD},$ respectively, so that $triangle AEF$ is equilateral. A square with vertex $B$ has sides that are parallel to those of $ABCD$ and a vertex on $overline{AE}.$ The length of a side of this smaller square is $frac{a-sqrt{b}}{c},$ where $a, b,$ and $c$ are positive integers and $b$ is not divisible by the square of any prime. Find $a+b+c.$

Problem 7

Find the number of ordered pairs of positive integers $(a,b)$ such that $a+b=1000$ and neither $a$ nor $b$ has a zero digit.

Problem 8

There is an unlimited supply of congruent equilateral triangles made of colored paper. Each triangle is a solid color with the same color on both sides of the paper. A large equilateral triangle is constructed from four of these paper triangles. Two large triangles are considered distinguishable if it is not possible to place one on the other, using translations, rotations, and/or reflections, so that their corresponding small triangles are of the same color.

Given that there are six different colors of triangles from which to choose, how many distinguishable large equilateral triangles may be formed? $[asy] size(50); pair A,B; A=(0,0); B=(2,0); pair C=rotate(60,A)*B; pair D, E, F; D = (1,0); E=rotate(60,A)*D; F=rotate(60,C)*E; draw(C--A--B--cycle); draw(D--E--F--cycle); [/asy]$

Problem 9

Circles $mathcal{C}_1, mathcal{C}_2,$ and $mathcal{C}_3$ have their centers at (0,0), (12,0), and (24,0), and have radii 1, 2, and 4, respectively. Line $t_1$ is a common internal tangent to $mathcal{C}_1$ and $mathcal{C}_2$ and has a positive slope, and line $t_2$ is a common internal tangent to $mathcal{C}_2$ and $mathcal{C}_3$ and has a negative slope. Given that lines $t_1$ and $t_2$ intersect at $(x,y),$ and that $x=p-qsqrt{r},$ where $p, q,$ and $r$ are positive integers and $r$ is not divisible by the square of any prime, find $p+q+r.$

Problem 10

Seven teams play a soccer tournament in which each team plays every other team exactly once. No ties occur, each team has a $50%$ chance of winning each game it plays, and the outcomes of the games are independent. In each game, the winner is awarded a point and the loser gets 0 points. The total points are accumulated to decide the ranks of the teams. In the first game of the tournament, team $A$ beats team $B.$ The probability that team $A$ finishes with more points than team $B$ is $m/n,$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Problem 11

A sequence is defined as follows $a_1=a_2=a_3=1,$ and, for all positive integers $n, a_{n+3}=a_{n+2}+a_{n+1}+a_n.$ Given that $a_{28}=6090307, a_{29}=11201821,$ and $a_{30}=20603361,$ find the remainder when $sum^{28}_{k=1} a_k$ is divided by 1000.

Problem 12

Equilateral $triangle ABC$ is inscribed in a circle of radius 2. Extend $overline{AB}$ through $B$ to point $D$ so that $AD=13,$ and extend $overline{AC}$ through $C$ to point $E$ so that $AE = 11.$ Through $D,$ draw a line $l_1$ parallel to $overline{AE},$ and through $E,$ draw a line $l_2$ parallel to $overline{AD}.$ Let $F$ be the intersection of $l_1$ and $l_2.$ Let $G$ be the point on the circle that is collinear with $A$ and $F$ and distinct from $A.$ Given that the area of $triangle CBG$ can be expressed in the form $frac{psqrt{q}}{r},$ where $p, q,$ and $r$ are positive integers, $p$ and $r$ are relatively prime, and $q$ is not divisible by the square of any prime, find $p+q+r.$

Problem 13

How many integers $N$ less than 1000 can be written as the sum of $j$ consecutive positive odd integers from exactly 5 values of $jge 1$ ?

Problem 14

Let $S_n$ be the sum of the reciprocals of the non-zero digits of the integers from $1$ to $10^n$ inclusive. Find the smallest positive integer n for which $S_n$ is an integer.

Problem 15

Given that $x, y,$ and $z$ are real numbers that satisfy:

$x = sqrt{y^2-frac{1}{16}}+sqrt{z^2-frac{1}{16}}$ $y = sqrt{z^2-frac{1}{25}}+sqrt{x^2-frac{1}{25}}$ $z = sqrt{x^2 - frac 1{36}}+sqrt{y^2-frac 1{36}}$ and that $x+y+z = frac{m}{sqrt{n}},$ where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime, find $m+n.$

2006AIME II详细解析

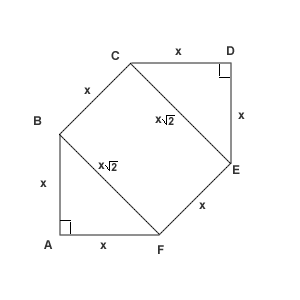Let the side length be called $x$ , so $x=AB=BC=CD=DE=EF=AF$ .The diagonal $BF=sqrt{AB^2+AF^2}=sqrt{x^2+x^2}=xsqrt{2}$ . Then the areas of the triangles AFB and CDE in total are $frac{x^2}{2}cdot 2$ , and the area of the rectangle BCEF equals $xcdot xsqrt{2}=x^2sqrt{2}$ Then we have to solve the equation

$2116(sqrt{2}+1)=x^2sqrt{2}+x^2$ .

$2116(sqrt{2}+1)=x^2(sqrt{2}+1)$

$2116=x^2$

$x=46$

Therefore, $AB$ is $boxed{46}$ .
By the Triangle Inequality and applying the well-known logarithmic property $log_{c} a cdot log_{c} b = log_{c} ab$ , we have that

$log_{10} 12 + log_{10} n > log_{10} 75$

$log_{10} 12n > log_{10} 75$

$12n > 75$

$n > frac{75}{12} = frac{25}{4} = 6.25$

Also,

$log_{10} 12 + log_{10} 75 > log_{10} n$

$log_{10} 12cdot75 > log_{10} n$

$n < 900$

Combining these two inequalities:

$[6.25 < n < 900]$

Thus $n$ is in the set $(6.25 , 900)$ ; the number of positive integer $n$ which satisfies this requirement is $boxed{893}$ .
Note that the product of the first $100$ positive odd integers can be written as $1cdot 3cdot 5cdot 7cdots 195cdot 197cdot 199=frac{1cdot 2cdots200}{2cdot4cdots200} = frac{200!}{2^{100}cdot 100!}$ Hence, we seek the number of threes in $200!$ decreased by the number of threes in $100!.$ There are $leftlfloor frac{200}{3}rightrfloor+leftlfloorfrac{200}{9}rightrfloor+leftlfloor frac{200}{27}rightrfloor+leftlfloorfrac{200}{81}rightrfloor =66+22+7+2=97$ threes in $200!$ and $leftlfloor frac{100}{3}rightrfloor+leftlfloorfrac{100}{9}rightrfloor+leftlfloor frac{100}{27}rightrfloor+leftlfloorfrac{100}{81}rightrfloor=33+11+3+1=48$ threes in $100!$
Therefore, we have a total of $97-48=49$ threes.

For more information, see also prime factorizations of a factorial.

We count the multiples of $3^k$ below 200 and subtract the count of multiples of $2cdot 3^k$ :

$[leftlfloor frac{200}{3}rightrfloor - leftlfloor frac{200}{6}rightrfloor +leftlfloorfrac{200}{9}rightrfloor - leftlfloor frac{200}{18}rightrfloor +leftlfloor frac{200}{27}rightrfloor - leftlfloor frac{200}{54}rightrfloor+leftlfloorfrac{200}{81}rightrfloor - leftlfloor frac{200}{162}rightrfloor]$ $[= 66 - 33 + 22 - 11 + 7 - 3 + 2 - 1 = 49.]$
Clearly, $a_6=1$ . Now, consider selecting $5$ of the remaining $11$ values. Sort these values in descending order, and sort the other $6$ values in ascending order. Now, let the $5$ selected values be $a_1$ through $a_5$ , and let the remaining $6$ be $a_7$ through ${a_{12}}$ . It is now clear that there is a bijection between the number of ways to select $5$ values from $11$ and ordered 12-tuples $(a_1,ldots,a_{12})$ . Thus, there will be ${11 choose 5}=462$ such ordered 12-tuples.There are $binom{12}{6}$ ways to choose 6 numbers from $(1,2,3,ldots,12)$ , and then there will only be one way to order them. And since that $a_6<a_7$ , only half of the choices will work, so the answer is $frac{binom{12}{6}}{2}=462$
Without loss of generality, assume that face $F$ has a 6, so the opposite face has a 1. Let $A(n)$ be the probability of rolling a number $n$ on one die and let $B(n)$ be the probability of rolling a number $n$ on the other die. 7 can be obtained by rolling a 2 and 5, 5 and 2, 3 and 4, or 4 and 3. Each has a probability of $frac{1}{6} cdot frac{1}{6} = frac{1}{36}$ , totaling $4 cdot frac{1}{36} = frac{1}{9}$ . Subtracting all these probabilities from $frac{47}{288}$ leaves $frac{15}{288}=frac{5}{96}$ chance of getting a 1 on die $A$ and a 6 on die $B$ or a 6 on die $A$ and a 1 on die $B$ : $[A(6)cdot B(1)+B(6)cdot A(1)=frac{5}{96}]$ Since the two dice are identical, $B(1)=A(1)$ and $B(6)=A(6)$ so $begin{align*}A(1)cdot A(6)+A(1)cdot A(6)&=frac{5}{96} A(1)cdot A(6)&=frac{5}{192}end{align*}$ Also, we know that $A(2)=A(3)=A(4)=A(5)=frac{1}{6}$ and that the total probability must be $1$ , so: $[A(1)+4 cdot frac{1}{6}+A(6)=frac{6}{6} Longrightarrow A(1)+A(6)=frac{1}{3}]$ Combining the equations:
$begin{align*}A(6)left(frac{1}{3}-A(6)right)&=frac{5}{192} 0 &= 192 left(A(6)right)^2 - 64 left(A(6)right) + 5 A(6)&=frac{64pmsqrt{64^2 - 4 cdot 5 cdot 192}}{2cdot192} =frac{5}{24}, frac{1}{8}end{align*}$ We know that $A(6)>frac{1}{6}$ , so it can't be $frac{1}{8}$ . Therefore, the probability is $frac{5}{24}$ and the answer is $5+24=boxed{29}$ .

Note also that the initial assumption that face $F$ was the face labelled 6 is unnecessary -- we would have carried out exactly the same steps and found exactly the same probability no matter which face it was. We could have labelled $A(6)$ as $p$ , for example, and replaced the others with variables too, but the notation would have been harder to follow.

We have that the cube probabilities to land on its faces are $frac{1}{6}$ , $frac{1}{6}$ , $frac{1}{6}$ , $frac{1}{6}$ , $frac{1}{6}+x$ , $frac{1}{6}-x$ we also know that the sum could be 7 only when the faces in each of the two tosses are opposite hence the probability to get a 7 is: $[4*((frac{1}{6})^2)+2(frac{1}{6}+x)(frac{1}{6}-x)=frac{47}{288}]$ multiplying by 288 we get: $[32+16(6x-1)(6x+1)=47 Longrightarrow 16(1-36x^2)=15]$ dividing by 16 and rearranging we get: $[frac{1}{16}=36x^2 longrightarrow x=frac{1}{24}]$ so the probability F which is greater than $frac{1}{6}$ is equal $frac{1}{6}+frac{1}{24}=frac{5}{24}longrightarrow 24+5=boxed{29}$
Call the vertices of the new square A', B', C', and D', in relation to the vertices of $ABCD$ , and define $s$ to be one of the sides of that square. Since the sides are parallel, by corresponding angles and AA~ we know that triangles $AA'D'$ and $D'C'E$ are similar. Thus, the sides are proportional: $frac{AA'}{A'D'} = frac{D'C'}{C'E} Longrightarrow frac{1 - s}{s} = frac{s}{1 - s - CE}$ . Simplifying, we get that $s^2 = (1 - s)(1 - s - CE)$ . $angle EAF$ is $60$ degrees, so $angle BAE = frac{90 - 60}{2} = 15$ . Thus, $cos 15 = cos (45 - 30) = frac{sqrt{6} + sqrt{2}}{4} = frac{1}{AE}$ , so $AE = frac{4}{sqrt{6} + sqrt{2}} cdot frac{sqrt{6} - sqrt{2}}{sqrt{6} - sqrt{2}} = sqrt{6} - sqrt{2}$ . Since $triangle AEF$ is equilateral, $EF = AE = sqrt{6} - sqrt{2}$ . $triangle CEF$ is a $45-45-90 triangle$ , so $CE = frac{AE}{sqrt{2}} = sqrt{3} - 1$ . Substituting back into the equation from the beginning, we get $s^2 = (1 - s)(2 - sqrt{3} - s)$ , so $(3 - sqrt{3})s = 2 - sqrt{3}$ . Therefore, $s = frac{2 - sqrt{3}}{3 - sqrt{3}} cdot frac{3 + sqrt{3}}{3 + sqrt{3}} = frac{3 - sqrt{3}}{6}$ , and $a + b + c = 3 + 3 + 6 = 12$ .

Here's an alternative geometric way to calculate $AE$ (as opposed to trigonometric): The diagonal $overline{AC}$ is made of the altitude of the equilateral triangle and the altitude of the $45-45-90 triangle$ . The former is $frac{AEsqrt{3}}{2}$ , and the latter is $frac{AE}{2}$ ; thus $frac{AEsqrt{3} + AE}{2} = AC = sqrt{2} Longrightarrow AE= sqrt{6}-sqrt{2}$ . The solution continues as above.

Since $triangle AFE$ is equilateral, $overline{AE} = overline{AF}$ . It follows that $overline{FC} = overline{EC}$ . Let $overline{FC} = x$ . Then, $overline{EF} = xsqrt{2}$ and $overline{DF} = 1-x$ .

$overline{AF} = sqrt{1+(1-x)^2} = xsqrt{2}$ .

Square both sides and combine/move terms to get $x^2+2x-2 = 0$ . Therefore $x = -1 + sqrt{3}$ and $x = -1 - sqrt{3}$ . The second solution is obviously extraneous, so $x = -1 + sqrt{3}$ .

Now, consider the square ABCD to be on the Cartesian Coordinate Plane with $A = (0,0)$ . Then, the line containing $overline{AF}$ has slope $frac{1}{2-sqrt{3}}$ and equation $y = frac{1}{2-sqrt{3}}x$ .

The distance from $overline{DC}$ to $overline{AF}$ is the distance from $y = 1$ to $y = frac{1}{2-sqrt{3}}x$ .

Similarly, the distance from $overline{AD}$ to $overline{AF}$ is the distance from $x = 0$ to $y = frac{1}{2-sqrt{3}}x$ .

For some value $x = s$ , these two distances are equal.

$(s-0) = (1 - (frac{1}{2-sqrt{3}})s)$

Solving for s, $s = frac{3 - sqrt{3}}{6}$ , and $a + b + c = 3 + 3 + 6 = 12$ .

Why not solve in terms of the side $x$ only (single-variable beauty)? By similar triangles we obtain that $BE=frac{x}{1-x}$ , therefore $CE=frac{1-2x}{1-x}$ . Then $AE=sqrt{2}*frac{1-2x}{1-x}$ . Using Pythagorean Theorem on $triangle{ABE}$ yields $frac{x^2}{(1-x)^2} + 1 = 2 * frac{(1-2x)^2}{(1-x)^2}$ . This means $6x^2-6x+1=0$ , and it's clear we take the smaller root: $x=frac{3-sqrt{3}}{6}$ . Answer: $boxed{12}$ .
There are $leftlfloorfrac{999}{10}rightrfloor = 99$ numbers up to 1000 that have 0 as their units digit. All of the other excluded possibilities are when $a$ or $b$ have a 0 in the tens digit, and since the equation is symmetric, we will just count when $a$ has a 0 in the tens digit and multiply by 2 (notice that the only time both $a$ and $b$ can have a 0 in the tens digit is when they are divisible by 100, which falls into the above category, so we do not have to worry about overcounting).Excluding the numbers divisible by 100, which were counted already, there are $9$ numbers in every hundred numbers that have a tens digit of 0 (this is true from 100 to 900), totaling $9 cdot 9 = 81$ such numbers; considering $b$ also and we have $81 cdot 2 = 162$ . Therefore, there are $999 - (99 + 162) = boxed{738}$ such ordered pairs.
If two of our big equilateral triangles have the same color for their center triangle and the same multiset of colors for their outer three triangles, we can carry one onto the other by a combination of rotation and reflection. Thus, to make two triangles distinct, they must differ either in their center triangle or in the collection of colors which make up their outer three triangles.There are 6 possible colors for the center triangle.
- There are ${6choose3} = 20$ possible choices for the three outer triangles, if all three have different colors.
- There are $6cdot 5 = 30$ (or $2 {6choose2}$ ) possible choices for the three outer triangles, if two are one color and the third is a different color.
- There are ${6choose1} = 6$ possible choices for the three outer triangles, if all three are the same color.
Thus, in total we have $6cdot(20 + 30 + 6) = 336$ total possibilities.

We apply burnsides lemma and consider 3 rotations of 120 degrees, 240 degrees, and 0 degrees. We also consider three reflections from the three lines of symmetry in the triangle. Thus, we have to divide by $3+3=6$ for our final count.

Case 1: 0 degree rotation. This is known as the identity rotation, and there are $6^4=1296$ choices because we don't have any restrictions.

Case 2: 120 degree rotation. Note that the three "outer" sides of the triangle have to be the same during this, and the middle one can be anything. We have $6*6=36$ choices from this.

Case 3: 240 degree rotation. Similar to the 120 degree rotation, each must be the same except for the middle. We have $6*6=36$ choices from this.

Case 4: symmetry about lines. We multiply by 3 for these because the amount of colorings fixed under symmetry are the exact same each time. Two triangles do not change under this, and they must be the same. The other two triangles (1 middle and 1 outer) can be anything because they stay the same during the reflection. We have $6*6*6=216$ ways for one symmetry. There are 3 symmetries, so there are $216*3=648$ combinations in all.

Now, we add our cases up: $1296+36+36+648=2016$ . We have to divide by 6, so $2016/6=boxed{336}$ distinguishable ways to color the triangle.

There are $6$ choices for the center triangle. Note that given any $3$ colors, there is a unique way to assign them to the corner triangles. We have $6$ different colors to choose from, so the number of ways to color the corner triangles is the same as the number of ways to arrange $6 - 1 = 5$ dividers and $3$ identical items. Therefore, our answer is
Call the centers $O_1, O_2, O_3$ , the points of tangency $r_1, r_2, s_1, s_2$ (with $r$ on $t_1$ and $s$ on $t_2$ , and $s_2$ on $mathcal{C}_2$ ), and the intersection of each common internal tangent to the X-axis $r, s$ . $triangle O_1r_1r sim triangle O_2r_2r$ since both triangles have a right angle and have vertical angles, and the same goes for $triangle O_2s_2s sim triangle O_3s_1s$ . By proportionality, we find that $O_1r = 4$ ; solving $triangle O_1r_1r$ by the Pythagorean theorem yields $r_1r = sqrt{15}$ . On $mathcal{C}_3$ , we can do the same thing to get $O_3s_1 = 4$ and $s_1s = 4sqrt{3}$ .The vertical altitude of each of $triangle O_1r_1r$ and $triangle O_3s_1s$ can each by found by the formula $c cdot h = a cdot b$ (as both products equal twice of the area of the triangle). Thus, the respective heights are $frac{sqrt{15}}{4}$ and $2sqrt{3}$ . The horizontal distance from each altitude to the intersection of the tangent with the x-axis can also be determined by the Pythagorean theorem: $sqrt{15 - frac{15}{16}} = frac{15}{4}$ , and by 30-60-90: $6$ .From this information, the slope of each tangent can be uncovered. The slope of $t_1 = frac{Delta y}{Delta x} = frac{frac{sqrt{15}}{4}}{frac{15}{4}} = frac{1}{sqrt{15}}$ . The slope of $t_2 = -frac{2sqrt{3}}{6} = -frac{1}{sqrt{3}}$ .The equation of $t_1$ can be found by substituting the point $r (4,0)$ into $y = frac{1}{sqrt{15}}x + b$ , so $y = frac{1}{sqrt{15}}x - frac{4}{sqrt{15}}$ . The equation of $t_2$ , found by substituting point $s (16,0)$ , is $y = frac{-1}{sqrt{3}}x + frac{16}{sqrt{3}}$ . Putting these two equations together results in the desired $frac{1}{sqrt{15}}x - frac{4}{sqrt{15}} = -frac{1}{sqrt{3}}x + frac{16}{sqrt{3}}$ $Longrightarrow x = frac{16sqrt{5} + 4}{sqrt{5} + 1} cdot frac{sqrt{5}-1}{sqrt{5}-1}$ $= frac{76 - 12sqrt{5}}{4}$ $= 19 - 3sqrt{5}$ . Thus, $p + q + r = 19 + 3 + 5 Longrightarrow boxed{027}$ .
The results of the five remaining games are independent of the first game, so by symmetry, the probability that scores higher than in these five games is equal to the probability that scores higher than . We let this probability be ; then the probability that and end with the same score in these five games is .Of these three cases (), the last is the easiest to calculate (see solution 2 for a way to directly calculate the other cases).There are ways to to have victories, and ways for to have victories. Summing for all values of , $1-2p = frac{1}{2^{5} times 2^{5}}left(sum_{k=0}^{5} {5choose k}^2right) = frac{1^2+5^2+10^2+10^2+5^2+1^2}{1024} = frac{126}{512}.$ Thus . The desired probability is the sum of the cases when , so the answer is , and .You can break this into cases based on how many rounds wins out of the remaining 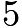games.
- If $A$ wins 0 games, then $B$ must win 0 games and the probability of this is $frac{{5 choose 0}}{2^5} frac{{5 choose 0}}{2^5} = frac{1}{1024}$ .
- If $A$ wins 1 games, then $B$ must win 1 or less games and the probability of this is $frac{{5 choose 1}}{2^5} frac{{5 choose 0}+{5 choose 1}}{2^5} = frac{30}{1024}$ .
- If $A$ wins 2 games, then $B$ must win 2 or less games and the probability of this is $frac{{5 choose 2}}{2^5} frac{{5 choose 0}+{5 choose 1}+{5 choose 2}}{2^5} = frac{160}{1024}$ .
- If $A$ wins 3 games, then $B$ must win 3 or less games and the probability of this is $frac{{5 choose 3}}{2^5} frac{{5 choose 0}+{5 choose 1}+{5 choose 2}+{5 choose 3}}{2^5} = frac{260}{1024}$ .
- If $A$ wins 4 games, then $B$ must win 4 or less games and the probability of this is $frac{{5 choose 4}}{2^5} frac{{5 choose 0}+{5 choose 1}+{5 choose 2}+{5 choose 3}+{5 choose 4}}{2^5} = frac{155}{1024}$ .
- If $A$ wins 5 games, then $B$ must win 5 or less games and the probability of this is $frac{{5 choose 5}}{2^5} frac{{5 choose 0}+{5 choose 1}+{5 choose 2}+{5 choose 3}+{5 choose 4}+{5 choose 5}}{2^5} = frac{32}{1024}$ .
Summing these 6 cases, we get $frac{638}{1024}$ , which simplifies to $frac{319}{512}$ , so our answer is $319 + 512 = boxed{831}$ .

We can apply the concept of generating functions here.

The generating function for $B$ is $(1 + 0x^{1})$ for the first game where $x^{n}$ is winning n games. Since $B$ lost the first game, the coefficient for $x^{1}$ is 0. The generating function for the next 5 games is $(1 + x)^{5}$ . Thus, the total generating function for number of games he wins is
```
.
```
The generating function for $A$ is the same except that it is multiplied by $x$ instead of $(1+0x)$ . Thus, the generating function for $A$ is

$1x + 5x^{2} + 10x^{3} + 10x^{4} + 5x^{5} + x^{6}$ .

The probability that $B$ wins 0 games is $frac{1}{32}$ . Since the coefficients for all $x^{n}$ where

$n geq 1$ sums to 32, the probability that $A$ wins more games is $frac{32}{32}$ .

Thus, the probability that $A$ has more wins than $B$ is $frac{1}{32} times frac{32}{32} + frac{5}{32} times frac{31}{32} + frac{10}{32} times frac{26}{32} + frac{10}{32} times frac{16}{32} + frac{5}{32} times frac{6}{32} +frac{1}{32} times frac{1}{32} = frac{638}{1024} = frac{319}{512}$ .

Thus, $319 + 512 = boxed{831}$ .

After the first game, there are $10$ games we care about-- those involving $A$ or $B$ . There are $3$ cases of these $10$ games: $A$ wins more than $B$ , $B$ wins more than $A$ , or $A$ and $B$ win the same number of games. Also, there are $2^{10} = 1024$ total outcomes. By symmetry, the first and second cases are equally likely, and the third case occurs $binom{5}{0}^2+binom{5}{1}^2+binom{5}{2}^2+binom{5}{3}^2+binom{5}{4}^2+binom{5}{5}^2 = binom{10}{5} = 252$ times, by a special case of Vandermonde's Identity. There are therefore $frac{1024-252}{2} = 386$ possibilities for each of the other two cases.

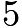If $B$ has more wins than $A$ in its $5$ remaining games, then $A$ cannot beat $B$ overall. However, if $A$ has more wins or if $A$ and $B$ are tied, $A$ will beat $B$ overall. Therefore, out of the $1024$ possibilites, $386+252 = 638$ ways where $A$ wins, so the desired probability is $frac{638}{1024} = frac{319}{512}$ , and $m+n=boxed{831}$ .
Define the sum as $s$ . Since $a_n = a_{n + 3} - a_{n + 2} - a_{n + 1}$ , the sum will be: $s = a_{28} + sum^{27}_{k=1} (a_{k+3}-a_{k+2}-a_{k+1}) s = a_{28} + left(sum^{30}_{k=4} a_{k} - sum^{29}_{k=3} a_{k}right) - left(sum^{28}_{k=2} a_{k}right) s = a_{28} + (a_{30} - a_{3}) - left(sum^{28}_{k=2} a_{k}right) = a_{28} + a_{30} - a_{3} - (s - a_{1}) s = -s + a_{28} + a_{30}$ Thus $s = frac{a_{28} + a_{30}}{2}$ , and $a_{28},,a_{30}$ are both given; the last four digits of their sum is $3668$ , and half of that is $1834$ . Therefore, the answer is $boxed{834}$ .Since the problem only asks for the first 28 terms and we only need to calculate mod 1000, we simply bash the first 28 terms: $a_{1}equiv 1 pmod {1000} newline a_{2}equiv 1 pmod {1000} newline a_{3}equiv 1 pmod {1000} newline a_{4}equiv 3 pmod {1000} newline a_{5}equiv 5 pmod {1000} newline cdots newline a_{25} equiv 793 pmod {1000} newline a_{26} equiv 281 pmod {1000} newline a_{27} equiv 233 pmod {1000} newline a_{28} equiv 307 pmod {1000}$ Adding all the residues shows the sum is congruent to $boxed{834}$ mod 1000.~ I-_-IAll terms in the sequence are sums of previous terms, so the sum of all terms up to a certain point must be some linear combination of the first three terms. Also, we are given $a_{28}, a_{29},$ and $a_{30}$ , so we can guess that there is some way to use them in a formula. Namely, we guess that there exists some $p, q, r$ such that $sum_{k=1}^{n}{a_k} = pa_n+qa_{n+1}+ra_{n+2}$ . From here, we list out the first few terms of the sequence and the cumulative sums, and with a little bit of substitution and algebra we see that $(p, q, r) = (frac{1}{2}, 0, frac{1}{2})$ , at least for the first few terms. From this, we have that $sum_{k=1}^{28}{a_k} = frac{a_{28}+a_{30}}{2} equiv{boxed{834}}(mod 1000)$ .
Notice that $angle{E} = angle{BGC} = 120^circ$ because $angle{A} = 60^circ$ . Also, $angle{GBC} = angle{GAC} = angle{FAE}$ because they both correspond to arc ${GC}$ . So $Delta{GBC} sim Delta{EAF}$ . $[[EAF] = frac12 (AE)(EF)sin angle AEF = frac12cdot11cdot13cdotsin{120^circ} = frac {143sqrt3}4.]$ Because the ratio of the area of two similar figures is the square of the ratio of the corresponding sides, $[GBC] = frac {BC^2}{AF^2}cdot[EAF] = frac {12}{11^2 + 13^2 - 2cdot11cdot13cdotcos120^circ}cdotfrac {143sqrt3}4 = frac {429sqrt3}{433}$ . Therefore, the answer is $429+433+3=boxed{865}$ .Solution by e_power_pi_times_iLet the center of the circle be $O$ and the origin. Then, $A (0,2)$ , $B (-sqrt{3}, -1)$ , $C (sqrt{3}, -1)$ . $D$ and $E$ can be calculated easily knowing $AD$ and $AE$ , $D (-dfrac{13}{2}, dfrac{-13sqrt{3}+4}{2})$ , $E (dfrac{11}{2}, dfrac{-11sqrt{3}+4}{2})$ . As $DF$ and $EF$ are parallel to $AE$ and $AD$ , $F (-1, -12sqrt{3}+2)$ . $G$ and $A$ is the intersection between $AF$ and circle $O$ . Therefore $G (-dfrac{48sqrt{3}}{433}, -dfrac{862}{433})$ . Using the Shoelace Theorem, $[CBG] = dfrac{429sqrt{3}}{433}$ , so the answer is $boxed{865}$ Lines $l_1$ and $l_2$ are constructed such that $AEFD$ is a parallelogram, hence $DF = 13$ . Since $BAC$ is equilateral with angle of $60^{circ}$ , angle $D$ is $120^{circ}$ . Use law of cosines to find $AF = sqrt{433}$ . Then use law of sines to find angle $BAG$ and $GAC$ . Next we use Ptolemy's Theorem on $ABGC$ to find that $CG + BG = AG$ . Next we use law of cosine on triangles $BAG$ and $GAC$ , solving for BG and CG respectively. Subtract the two equations and divide out a $BG + CG$ to find the value of $CG - BG$ . Next, $AG = 2cdot R cos{theta}$ , where R is radius of circle $= 2$ and $theta =$ angle $BAG$ . We already know sine of the angle so find cosine, hence we have found $AG$ . At this point it is system of equation yielding $CG = frac{26sqrt{3}}{sqrt{433}}$ and $BG = frac{22sqrt{3}}{sqrt{433}}$ . Given $[CBG] = frac{BC cdot CG cdot BG}{4R}$ , and $BC = 2sqrt{3}$ by $30-60-90$ triangle, we can evaluate to find $[CBG] = frac{429sqrt{3}}{433}$ , to give answer = $boxed{865}$ .
Let the first odd integer be , . Then the final odd integer is . The odd integers form an arithmetic sequence with sum . Thus, is a factor of .Since , it follows that and .Since there are exactly 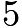values of that satisfy the equation, there must be either or factors of . This means or . Unfortunately, we cannot simply observe prime factorizations of because the factor does not cover all integers for any given value of .Instead we do some casework:
- If $N$ is odd, then $j$ must also be odd. For every odd value of $j$ , $2n+j$ is also odd, making this case valid for all odd $j$ . Looking at the forms above and the bound of $1000$ , $N$ must be
$[(3^2cdot5^2), (3^2cdot7^2), (3^4cdot5), (3^4cdot7), (3^4cdot 11)]$

Those give 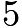$5$ possibilities for odd $N$ .
- If $N$ is even, then $j$ must also be even. Substituting $j=2k$ , we get
$[N = 4k(n+k) Longrightarrow frac{N}{4} = k(n+k)]$

Now we can just look at all the prime factorizations since $(n+k)$ cover the integers for any $k$ . Note that our upper bound is now $250$ :

$[frac{N}{4} = (2^2cdot3^2),(2^2cdot5^2),(2^2cdot7^2), (3^2cdot5^2), (2^4cdot3), (2^4cdot5), (2^4cdot7), (2^4cdot11), (2^4cdot13), (3^4cdot2)]$

Those give $10$ possibilities for even $N$ .

The total number of integers $N$ is $5 + 10 = boxed{015}$ .
Let $K = sum_{i=1}^{9}{frac{1}{i}}$ . Examining the terms in $S_1$ , we see that $S_1 = K + 1$ since each digit $n$ appears once and 1 appears an extra time. Now consider writing out $S_2$ . Each term of $K$ will appear 10 times in the units place and 10 times in the tens place (plus one extra 1 will appear), so $S_2 = 20K + 1$ .In general, we will have that $S_n = (n10^{n-1})K + 1$ because each digit will appear $10^{n - 1}$ times in each place in the numbers $1, 2, ldots, 10^{n} - 1$ , and there are $n$ total places.The denominator of $K$ is $D = 2^3cdot 3^2cdot 5cdot 7$ . For $S_n$ to be an integer, $n10^{n-1}$ must be divisible by $D$ . 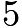Since $10^{n-1}$ only contains the factors $2$ and $5$ (but will contain enough of them when $n geq 3$ ), we must choose $n$ to be divisible by $3^2cdot 7$ . Since we're looking for the smallest such $n$ , the answer is $boxed{63}$ .
Let $triangle XYZ$ be a triangle with sides of length $x, y$ and $z$ , and suppose this triangle is acute (so all altitudes are on the interior of the triangle). Let the altitude to the side of length $x$ be of length $h_x$ , and similarly for $y$ and $z$ . Then we have by two applications of the Pythagorean Theorem that $x = sqrt{y^2 - h_x^2} + sqrt{z^2 - h_x^2}$ . As a function of $h_x$ , the RHS of this equation is strictly decreasing, so it takes each value in its range exactly once. Thus we must have that $h_x^2 = frac1{16}$ and so $h_x = frac{1}4$ and similarly $h_y = frac15$ and $h_z = frac16$ .Since the area of the triangle must be the same no matter how we measure, $xcdot h_x = ycdot h_y = z cdot h_z$ and so $frac x4 = frac y5 = frac z6 = 2A$ and $x = 8A, y = 10A$ and $z = 12A$ . The semiperimeter of the triangle is $s = frac{8A + 10A + 12A}{2} = 15A$ so by Heron's formula we have $A = sqrt{15A cdot 7A cdot 5A cdot 3A} = 15A^2sqrt{7}$ . Thus $A = frac{1}{15sqrt{7}}$ and $x + y + z = 30A = frac2{sqrt{7}}$ and the answer is $2 + 7 = boxed{9}$ .Justification that there is an acute triangle with sides of length $x, y$ and $z$ :Note that $x, y$ and $z$ are each the sum of two positive square roots of real numbers, so $x, y, z geq 0$ . (Recall that, by AIME convention, all numbers (including square roots) are taken to be real unless otherwise indicated.) Also, $sqrt{y^2-frac{1}{16}} < sqrt{y^2} = y$ , so we have $x < y + z$ , $y < z + x$ and $z < x + y$ . But these conditions are exactly those of the triangle inequality, so there does exist such a triangle.