Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2006AIME I真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月9日下午4:53

2006AIME I真题及答案解析

答案解析请参考文末

Problem 1

In quadrilateral $ABCD , angle B$ is a right angle, diagonal $overline{AC}$ is perpendicular to $overline{CD}, AB=18, BC=21,$ and $CD=14.$ Find the perimeter of $ABCD.$

Problem 2

Let set $mathcal{A}$ be a 90-element subset of ${1,2,3,ldots,100},$ and let $S$ be the sum of the elements of $mathcal{A}.$ Find the number of possible values of $S.$

Problem 3

Find the least positive integer such that when its leftmost digit is deleted, the resulting integer is $1/29$ of the original integer.

Problem 4

Let $N$ be the number of consecutive 0's at the right end of the decimal representation of the product $1!2!3!4!cdots99!100!.$ Find the remainder when $N$ is divided by 1000.

Problem 5

The number $sqrt{104sqrt{6}+468sqrt{10}+144sqrt{15}+2006}$ can be written as $asqrt{2}+bsqrt{3}+csqrt{5},$ where $a, b,$ and $c$ are positive integers. Find $acdot bcdot c.$

Problem 6

Let $mathcal{S}$ be the set of real numbers that can be represented as repeating decimals of the form $0.overline{abc}$ where $a, b, c$ are distinct digits. Find the sum of the elements of $mathcal{S}.$

Problem 7

An angle is drawn on a set of equally spaced parallel lines as shown. The ratio of the area of shaded region $mathcal{C}$ to the area of shaded region $mathcal{B}$ is 11/5. Find the ratio of shaded region $mathcal{D}$ to the area of shaded region $mathcal{A}.$

Problem 8

Hexagon $ABCDEF$ is divided into five rhombuses, $mathcal{P, Q, R, S,}$ and $mathcal{T,}$ as shown. Rhombuses $mathcal{P, Q, R,}$ and $mathcal{S}$ are congruent, and each has area $sqrt{2006}.$ Let $K$ be the area of rhombus $mathcal{T}.$ Given that $K$ is a positive integer, find the number of possible values for $K.$

Problem 9

The sequence $a_1, a_2, ldots$ is geometric with $a_1=a$ and common ratio $r,$ where $a$ and $r$ are positive integers. Given that $log_8 a_1+log_8 a_2+cdots+log_8 a_{12} = 2006,$ find the number of possible ordered pairs $(a,r).$

Problem 10

Eight circles of diameter 1 are packed in the first quadrant of the coordinate plane as shown. Let region $mathcal{R}$ be the union of the eight circular regions. Line $l,$ with slope 3, divides $mathcal{R}$ into two regions of equal area. Line $l$ 's equation can be expressed in the form $ax=by+c,$ where $a, b,$ and $c$ are positive integers whose greatest common divisor is 1. Find $a^2+b^2+c^2.$

$[asy] unitsize(0.50cm); draw((0,-1)--(0,6)); draw((-1,0)--(6,0)); draw(shift(1,1)*unitcircle); draw(shift(1,3)*unitcircle); draw(shift(1,5)*unitcircle); draw(shift(3,1)*unitcircle); draw(shift(3,3)*unitcircle); draw(shift(3,5)*unitcircle); draw(shift(5,1)*unitcircle); draw(shift(5,3)*unitcircle); [/asy]$

Problem 11

A collection of 8 cubes consists of one cube with edge-length $k$ for each integer $k, 1 le k le 8.$ A tower is to be built using all 8 cubes according to the rules:

Any cube may be the bottom cube in the tower.
The cube immediately on top of a cube with edge-length $k$ must have edge-length at most $k+2.$

Let $T$ be the number of different towers than can be constructed. What is the remainder when $T$ is divided by 1000?

Problem 12

Find the sum of the values of $x$ such that $cos^3 3x+ cos^3 5x = 8 cos^3 4x cos^3 x,$ where $x$ is measured in degrees and $100< x< 200.$

Problem 13

For each even positive integer $x,$ let $g(x)$ denote the greatest power of 2 that divides $x.$ For example, $g(20)=4$ and $g(16)=16.$ For each positive integer $n,$ let $S_n=sum_{k=1}^{2^{n-1}}g(2k).$ Find the greatest integer $n$ less than 1000 such that $S_n$ is a perfect square.

Problem 14

A tripod has three legs each of length 5 feet. When the tripod is set up, the angle between any pair of legs is equal to the angle between any other pair, and the top of the tripod is 4 feet from the ground. In setting up the tripod, the lower 1 foot of one leg breaks off. Let $h$ be the height in feet of the top of the tripod from the ground when the broken tripod is set up. Then $h$ can be written in the form $frac m{sqrt{n}},$ where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. Find $lfloor m+sqrt{n}rfloor.$ (The notation $lfloor xrfloor$ denotes the greatest integer that is less than or equal to $x.$ )

Problem 15

Given that a sequence satisfies $x_0=0$ and $|x_k|=|x_{k-1}+3|$ for all integers $kge 1,$ find the minimum possible value of $|x_1+x_2+cdots+x_{2006}|.$

2006AIME I详细解析

From the problem statement, we construct the following diagram: $[asy] pointpen = black; pathpen = black + linewidth(0.65); pair C=(0,0), D=(0,-14),A=(-(961-196)^.5,0),B=IP(circle(C,21),circle(A,18)); D(MP("A",A,W)--MP("B",B,N)--MP("C",C,E)--MP("D",D,E)--A--C); D(rightanglemark(A,C,D,40)); D(rightanglemark(A,B,C,40)); [/asy]$ Using the Pythagorean Theorem:
$(AD)^2 = (AC)^2 + (CD)^2$

$(AC)^2 = (AB)^2 + (BC)^2$

Substituting $(AB)^2 + (BC)^2$ for $(AC)^2$ :

$(AD)^2 = (AB)^2 + (BC)^2 + (CD)^2$

Plugging in the given information:

$(AD)^2 = (18)^2 + (21)^2 + (14)^2$

$(AD)^2 = 961$

$(AD)= 31$

So the perimeter is $18+21+14+31=84$ , and the answer is $boxed{084}$ .
The smallest $S$ is $1+2+ ldots +90 = 91 cdot 45 = 4095$ . The largest $S$ is $11+12+ ldots +100=111cdot 45=4995$ . All numbers between $4095$ and $4995$ are possible values of S, so the number of possible values of S is $4995-4095+1=901$ .Alternatively, for ease of calculation, let set $mathcal{B}$ be a 10-element subset of ${1,2,3,ldots,100}$ , and let $T$ be the sum of the elements of $mathcal{B}$ . Note that the number of possible $S$ is the number of possible $T=5050-S$ . The smallest possible $T$ is $1+2+ ldots +10 = 55$ and the largest is $91+92+ ldots + 100 = 955$ , so the number of possible values of T, and therefore S, is $955-55+1=boxed{901}$ .
Suppose the original number is $N = overline{a_na_{n-1}ldots a_1a_0},$ where the $a_i$ are digits and the first digit, $a_n,$ is nonzero. Then the number we create is $N_0 = overline{a_{n-1}ldots a_1a_0},$ so $[N = 29N_0.]$ But $N$ is $N_0$ with the digit $a_n$ added to the left, so $N = N_0 + a_n cdot 10^n.$ Thus, $[N_0 + a_ncdot 10^n = 29N_0]$ $[a_n cdot 10^n = 28N_0.]$ The right-hand side of this equation is divisible by seven, so the left-hand side must also be divisible by seven. The number $10^n$ is never divisible by $7,$ so $a_n$ must be divisible by $7.$ But $a_n$ is a nonzero digit, so the only possibility is $a_n = 7.$ This gives $[7 cdot 10^n = 28N_0]$ or $[10^n = 4N_0.]$ Now, we want to minimize both $n$ and $N_0,$ so we take $N_0 = 25$ and $n = 2.$ Then $[N = 7 cdot 10^2 + 25 = boxed{725},]$ and indeed, $725 = 29 cdot 25.$ $square$
A number in decimal notation ends in a zero for each power of ten which divides it. Thus, we need to count both the number of 5s and the number of 2s dividing into our given expression. Since there are clearly more 2s than 5s, it is sufficient to count the number of 5s.One way to do this is as follows: $96$ of the numbers $1!, 2!, 3!, 100!$ have a factor of $5$ . $91$ have a factor of $10$ . $86$ have a factor of $15$ . And so on. This gives us an initial count of $96 + 91 + 86 + ldots + 1$ . Summing this arithmetic series of $20$ terms, we get $970$ . However, we have neglected some powers of $5$ - every $n!$ term for $ngeq25$ has an additional power of $5$ dividing it, for $76$ extra; every n! for $ngeq 50$ has one more in addition to that, for a total of $51$ extra; and similarly there are $26$ extra from those larger than $75$ and $1$ extra from $100$ . Thus, our final total is $970 + 76 + 51 + 26 + 1 = 1124$ , and the answer is $boxed{124}$ .
We begin by equating the two expressions: $[asqrt{2}+bsqrt{3}+csqrt{5} = sqrt{104sqrt{6}+468sqrt{10}+144sqrt{15}+2006}]$ Squaring both sides yields: $[2absqrt{6} + 2acsqrt{10} + 2bcsqrt{15} + 2a^2 + 3b^2 + 5c^2 = 104sqrt{6}+468sqrt{10}+144sqrt{15}+2006]$ Since $a$ , $b$ , and $c$ are integers, we can match coefficients: $begin{align*} 2absqrt{6} &= 104sqrt{6} 2acsqrt{10} &=468sqrt{10} 2bcsqrt{15} &=144sqrt{15} 2a^2 + 3b^2 + 5c^2 &=2006 end{align*}$ Solving the first three equations gives: $begin{eqnarray*}ab &=& 52 ac &=& 234 bc &=& 72 end{eqnarray*}$
Multiplying these equations gives $(abc)^2 = 52 cdot 234 cdot 72 = 2^63^413^2 Longrightarrow abc = boxed{936}$ .

We realize that the quantity under the largest radical is a perfect square and attempt to rewrite the radicand as a square. Start by setting $x=sqrt{2}$ , $y=sqrt{3}$ , and $z=sqrt{5}$ . Since

$[(px+qy+rz)^2=p^2x^2+q^2y^2+r^2z^2+2(pqxy+prxz+qryz)]$

we attempt to rewrite the radicand in this form:

$[2006+2(52xy+234xz+72yz)]$

Factoring, we see that $52=13cdot4$ , $234=13cdot18$ , and $72=4cdot18$ . Setting $p=13$ , $q=4$ , and $r=18$ , we see that

$[2006=13^2x^2+4^2y^2+18^2z^2=169cdot2+16cdot3+324cdot5]$

so our numbers check. Thus $104sqrt{2}+468sqrt{3}+144sqrt{5}+2006=(13sqrt{2}+4sqrt{3}+18sqrt{5})^2$ . Square rooting gives us $13sqrt{2}+4sqrt{3}+18sqrt{5}$ and our answer is $13cdot4cdot18=boxed{936}$
Numbers of the form $0.overline{abc}$ can be written as $frac{abc}{999}$ . There are $10times9times8=720$ such numbers. Each digit will appear in each place value $frac{720}{10}=72$ times, and the sum of the digits, 0 through 9, is 45. So the sum of all the numbers is $frac{45times72times111}{999}= boxed{360}$ .Alternatively, for every number, $0.overline{abc}$ , there will be exactly one other number, such that when they are added together, the sum is $0.overline{999}$ , or, more precisely, 1. As an example, $.overline{123}+.overline{876}=.overline{999} Longrightarrow 1$ .Thus, the solution can be determined by dividing the total number of permutations by 2. The answer is $frac{10 cdot 9 cdot 8}{2} = frac{720}{2}= boxed{360}$ .Another method, albeit a little risky, that can be used is to note that the numbers between 1 and 999 with distinct digits average out to $frac{999}{2}$ . Then the total sum becomes $frac{frac{999}{2}times720}{999}$ which reduces to $boxed{360}$
Note that the apex of the angle is not on the parallel lines. Set up a coordinate proof.Let the set of parallel lines be perpendicular to the x-axis, such that they cross it at $0, 1, 2 ldots$ . The base of region $mathcal{A}$ is on the line $x = 1$ . The bigger base of region $mathcal{D}$ is on the line $x = 7$ . Let the top side of the angle be $y = x - s$ and the bottom side be x-axis, as dividing the angle doesn't change the problem.Since the area of the triangle is equal to $frac{1}{2}bh$ , $[frac{textrm{Region }mathcal{C}}{textrm{Region }mathcal{B}} = frac{11}{5} = frac{frac 12(5-s)^2 - frac 12(4-s)^2}{frac 12(3-s)^2 - frac12(2-s)^2}]$ Solve this to find that $s = frac{5}{6}$ .Using the same reasoning as above, we get $frac{textrm{Region }mathcal{D}}{textrm{Region }mathcal{A}} = frac{frac 12(7-s)^2 - frac 12(6-s)^2}{frac 12(1-s)^2}$ , which is $boxed{408}$ .Note that the sections between the two transversals can be divided into one small triangle and a number of trapezoids. Let one side length (not on a parallel line) of the small triangle be $x$ and the area of it be $x^2$ . Also, let all sections of the line on the same side as the side with length $x$ on a trapezoid be equal to $1$ .
Move on to the second-smallest triangle, formed by attaching this triangle with the next trapezoid. Parallel lines give us similar triangles, so we know the proportion of this triangle to the previous triangle is $(frac{x+1}{x})^2$ . Multiplying, we get $(x+1)^2$ as the area of the triangle, so the area of the trapezoid is $2x+1$ . Repeating this process, we get that the area of B is $2x+3$ , the area of C is $2x+7$ , and the area of D is $2x+11$ .

We can now use the given condition that the ratio of C and B is $frac{11}{5}$ .

$frac{11}{5} = frac{2x+7}{2x+3}$ gives us $x = frac{1}{6}$

So now we compute the ratio of D and A, which is $frac{2(frac{1}{6} + 11)}{(frac{1}{6})^2} = boxed{408.}$
Let $x$ denote the common side length of the rhombi. Let $y$ denote one of the smaller interior angles of rhombus $mathcal{P}$ . Then $x^2sin(y)=sqrt{2006}$ . We also see that $K=x^2sin(2y) Longrightarrow K=2x^2sin y cdot cos y Longrightarrow K = 2sqrt{2006}cdot cos y$ . Thus $K$ can be any positive integer in the interval $(0, 2sqrt{2006})$ . $2sqrt{2006} = sqrt{8024}$ and $89^2 = 7921 < 8024 < 8100 = 90^2$ , so $K$ can be any integer between 1 and 89, inclusive. Thus the number of positive values for $K$ is $boxed{089}$ .
$[log_8 a_1+log_8 a_2+ldots+log_8 a_{12}= log_8 a+log_8 (ar)+ldots+log_8 (ar^{11}) = log_8(acdot arcdot ar^2cdot cdots cdot ar^{11}) = log_8 (a^{12}r^{66})]$ So our question is equivalent to solving $log_8 (a^{12}r^{66})=2006$ for $a, r$ positive integers. $a^{12}r^{66}=8^{2006} = (2^3)^{2006} = (2^6)^{1003}$ so $a^{2}r^{11}=2^{1003}$ .The product of $a^2$ and $r^{11}$ is a power of 2. Since both numbers have to be integers, this means that $a$ and $r$ are themselves powers of 2. Now, let $a=2^x$ and $r=2^y$ : $begin{eqnarray*}(2^x)^2cdot(2^y)^{11}&=&2^{1003} 2^{2x}cdot 2^{11y}&=&2^{1003} 2x+11y&=&1003 y&=&frac{1003-2x}{11} end{eqnarray*}$ For $y$ to be an integer, the numerator must be divisible by $11$ . This occurs when $x=1$ because $1001=91*11$ . Because only even integers are being subtracted from $1003$ , the numerator never equals an even multiple of $11$ . Therefore, the numerator takes on the value of every odd multiple of $11$ from $11$ to $1001$ . Since the odd multiples are separated by a distance of $22$ , the number of ordered pairs that work is $1 + frac{1001-11}{22}=1 + frac{990}{22}=46$ . (We must add 1 because both endpoints are being included.) So the answer is $boxed{046}$ .For the step above, you may also simply do $1001/11 + 1 = 91 + 1 = 92$ to find how many multiples of $11$ there are in between $11$ and $1001$ . Then, divide $92/2$ = $boxed{046}$ to find only the odd solutions. $-XxHalo711$

Another way is to write

$x = frac{1003-11y}2$

Since $1003/11 = 91 + 2/11$ , the answer is just the number of odd integers in $[1,91]$ , which is, again, $boxed{046}$ .

Using the above method, we can derive that $a^{2}r^{11} = 2^{1003}$ . Now, think about what happens when r is an even power of 2. Then $a^{2}$ must be an odd power of 2 in order to satisfy the equation which is clearly not possible. Thus the only restriction r has is that it must be an odd power of 2, so $2^{1}$ , $2^{3}$ , $2^{5}$ .... all work for r, until r hits $2^{93}$ , when it gets greater than $2^{1003}$ , so the greatest value for r is $2^{91}$ . All that's left is to count the number of odd integers between 1 and 91 (inclusive), which yields $boxed{046}$ .
The line passing through the tangency point of the bottom left circle and the one to its right and through the tangency of the top circle in the middle column and the one beneath it is the line we are looking for: a line passing through the tangency of two circles cuts congruent areas, so our line cuts through the four aforementioned circles splitting into congruent areas, and there are an additional two circles on each side. The line passes through $left(1,frac 12right)$ and $left(frac 32,2right)$ , which can be easily solved to be $6x = 2y + 5$ . Thus, $a^2 + b^2 + c^2 = boxed{065}$ .Assume that if unit squares are drawn circumscribing the circles, then the line will divide the area of the concave hexagonal region of the squares equally (as of yet, there is no substantiation that such would work, and definitely will not work in general). Denote the intersection of the line and the x-axis as $(x, 0)$ .The line divides the region into 2 sections. The left piece is a trapezoid, with its area $frac{1}{2}((x) + (x+1))(3) = 3x + frac{3}{2}$ . The right piece is the addition of a trapezoid and a rectangle, and the areas are $frac{1}{2}((1-x) + (2-x))(3)$ and $2 cdot 1 = 2$ , totaling $frac{13}{2} - 3x$ . Since we want the two regions to be equal, we find that $3x + frac 32 = frac {13}2 - 3x$ , so $x = frac{5}{6}$ .We have that $left(frac 56, 0right)$ is a point on the line of slope 3, so $y - 0 = 3left(x - frac 56right) Longrightarrow 6x = 2y + 5$ . Our answer is $2^2 + 5^2 + 6^2 = 65$ .We now assess the validity of our starting assumption. We can do that by seeing that our answer passes through the tangency of the two circles, cutting congruent areas, a result explored in solution 1.
We proceed recursively. Suppose we can build $T_m$ towers using blocks of size $1, 2, ldots, m$ . How many towers can we build using blocks of size $1, 2, ldots, m, m + 1$ ? If we remove the block of size $m + 1$ from such a tower (keeping all other blocks in order), we get a valid tower using blocks $1, 2, ldots, m$ . Given a tower using blocks $1, 2, ldots, m$ (with $m geq 2$ ), we can insert the block of size $m + 1$ in exactly 3 places: at the beginning, immediately following the block of size $m - 1$ or immediately following the block of size $m$ . Thus, there are 3 times as many towers using blocks of size $1, 2, ldots, m, m + 1$ as there are towers using only $1, 2, ldots, m$ . There are 2 towers which use blocks $1, 2$ , so there are $2cdot 3^6 = 1458$ towers using blocks $1, 2, ldots, 8$ , so the answer is $boxed{458}$ .(Note that we cannot say, "there is one tower using the block $1$ , so there are $3^7$ towers using the blocks $1, 2, ldots, 8$ ." The reason this fails is that our recursion only worked when $m geq 2$ : when $m = 1$ , there are only 2 places to insert a block of size $m + 1 = 2$ , at the beginning or at the end, rather than the 3 places we have at later stages. Also, note that this method generalizes directly to seeking the number of towers where we change the second rule to read, "The cube immediately on top of a cube with edge-length $k$ must have edge-length at most $k + n$ ," where $n$ can be any fixed integer.)
Observe that $2cos 4xcos x = cos 5x + cos 3x$ by the sum-to-product formulas. Defining $a = cos 3x$ and $b = cos 5x$ , we have $a^3 + b^3 = (a+b)^3 rightarrow ab(a+b) = 0$ . But $a+b = 2cos 4xcos x$ , so we require $cos x = 0$ , $cos 3x = 0$ , $cos 4x = 0$ , or $cos 5x = 0$ .Hence we see by careful analysis of the cases that the solution set is $A = {150, 126, 162, 198, 112.5, 157.5}$ and thus $sum_{x in A} x = boxed{906}$ .
Given $g : x mapsto max_{j : 2^j | x} 2^j$ , consider $S_n = g(2) + cdots + g(2^n)$ . Define $S = {2, 4, ldots, 2^n}$ . There are $2^0$ elements of $S$ that are divisible by $2^n$ , $2^1 - 2^0 = 2^0$ elements of $S$ that are divisible by $2^{n-1}$ but not by $2^n, ldots,$ and $2^{n-1}-2^{n-2} = 2^{n-2}$ elements of $S$ that are divisible by $2^1$ but not by $2^2$ .Thus $begin{align*} S_n &= 2^0cdot2^n + 2^0cdot2^{n-1} + 2^1cdot2^{n-2} + cdots + 2^{n-2}cdot2^1 &= 2^n + (n-1)2^{n-1} &= 2^{n-1}(n+1).end{align*}$ Let $2^k$ be the highest power of $2$ that divides $n+1$ . Thus by the above formula, the highest power of $2$ that divides $S_n$ is $2^{k+n-1}$ . For $S_n$ to be a perfect square, $k+n-1$ must be even. If $k$ is odd, then $n+1$ is even, hence $k+n-1$ is odd, and $S_n$ cannot be a perfect square. Hence $k$ must be even. In particular, as $n<1000$ , we have five choices for $k$ , namely $k=0,2,4,6,8$ .If $k=0$ , then $n+1$ is odd, so $k+n-1$ is odd, hence the largest power of $2$ dividing $S_n$ has an odd exponent, so $S_n$ is not a perfect square.In the other cases, note that $k+n-1$ is even, so the highest power of $2$ dividing $S_n$ will be a perfect square. In particular, $S_n$ will be a perfect square if and only if $(n+1)/2^{k}$ is an odd perfect square.If $k=2$ , then $n<1000$ implies that $frac{n+1}{4} le 250$ , so we have $n+1 = 4, 4 cdot 3^2, ldots, 4 cdot 13^2, 4cdot 3^2 cdot 5^2$ .If $k=4$ , then $n<1000$ implies that $frac{n+1}{16} le 62$ , so $n+1 = 16, 16 cdot 3^2, 16 cdot 5^2, 16 cdot 7^2$ .If $k=6$ , then $n<1000$ implies that $frac{n+1}{64}le 15$ , so $n+1=64,64cdot 3^2$ .
If $k=8$ , then $n<1000$ implies that $frac{n+1}{256}le 3$ , so $n+1=256$ .

Comparing the largest term in each case, we find that the maximum possible $n$ such that $S_n$ is a perfect square is $4cdot 3^2 cdot 5^2 - 1 = boxed{899}$ .

First note that $g(k)=1$ if $k$ is odd and $2g(k/2)$ if $k$ is even. so $S_n=sum_{k=1}^{2^{n-1}}g(2k). = sum_{k=1}^{2^{n-1}}2g(k) = 2sum_{k=1}^{2^{n-1}}g(k) = 2sum_{k=1}^{2^{n-2}} g(2k-1)+g(2k).$ $2k-1$ must be odd so this reduces to $2sum_{k=1}^{2^{n-2}}1+g(2k) = 2(2^{n-2}+sum_{k=1}^{2^n-2}g(2k)).$ Thus $S_n=2(2^{n-2}+S_{n-1})=2^{n-1}+2S_{n-1}.$ Further noting that $S_0=1$ we can see that $S_n=2^{n-1}cdot (n-1)+2^ncdot S_0=2^{n-1}cdot (n-1)+2^{n-1}cdot2=2^{n-1}cdot (n+1).$ which is the same as above. To simplify the process of finding the largest square $S_n$ we can note that if $n-1$ is odd then $n+1$ must be exactly divisible by an odd power of $2$ . However, this means $n+1$ is even but it cannot be. Thus $n-1$ is even and $n+1$ is a large even square. The largest even square $< 1000$ is $900$ so $n+1= 900 => n= boxed{899}$
We will use $[...]$ to denote volume (four letters), area (three letters) or length (two letters).Let $T$ be the top of the tripod, $A,B,C$ are end points of three legs. Let $S$ be the point on $TA$ such that $[TS] = 4$ and $[SA] = 1$ . Let $O$ be the center of the base equilateral triangle $ABC$ . Let $M$ be the midpoint of segment $BC$ . Let $h$ be the distance from $T$ to the triangle $SBC$ ( $h$ is what we want to find).We have the volume ratio $frac {[TSBC]}{[TABC]} = frac {[TS]}{[TA]} = frac {4}{5}$ .So $frac {hcdot [SBC]}{[TO]cdot [ABC]} = frac {4}{5}$ .We also have the area ratio $frac {[SBC]}{[ABC]} = frac {[SM]}{[AM]}$ .The triangle $TOA$ is a $3-4-5$ right triangle so $[AM] = frac {3}{2}cdot[AO] = frac {9}{2}$ and $cos{angle{TAO}} = frac {3}{5}$ .Applying Law of Cosines to the triangle $SAM$ with $[SA] = 1$ , $[AM] = frac {9}{2}$ and $cos{angle{SAM}} = frac {3}{5}$ , we find:
$[SM] = frac {sqrt {5cdot317}}{10}.$ Putting it all together, we find $h = frac {144}{sqrt {5cdot317}}$ .

$lfloor 144+sqrt{5 cdot 317}rfloor =144+ lfloor sqrt{5 cdot 317}rfloor =144+lfloor sqrt{1585} rfloor =144+39=boxed{183}$ .We note that $AO=3$ . From this we can derive that the side length of the equilateral is $3sqrt{3}$ . We now use 3D coordinate geometry. $[A = (0,0,0)]$ $[B = (3sqrt{3},0,0)]$ $[C = (frac{3sqrt{3}}{2}, frac{9}{2}, 0)]$ $[T = (frac{3sqrt{3}}{2}, frac{3}{2}, 4)]$ $[S= (frac{3sqrt{3}}{10}, frac{3}{10}, frac{4}{5})]$ We know three points of plane $SCB$ hence we can write out the equation for the plane. Plane $SCB$ can be expressed as $[4sqrt{3}x+4y+39z-36=0.]$

Applying the distance between a point and a plane formula.

$[frac{ax+by+cz+d}{sqrt{a^{2}+b^{2}+c^{2}}} = frac{4sqrt{3} cdot frac{3sqrt{3}}{2} + 4cdot frac{3}{2} + 39 cdot 4 -36}{sqrt{(4sqrt{3})^2+4^2+39^2}} = frac{144}{sqrt{1585}}]$

$[lfloor m+sqrt{n}rfloor = lfloor 144+sqrt{1585}rfloor = 183]$
Suppose $b_{i} = frac {x_{i}}3$ . We have $[sum_{i = 1}^{2006}b_{i}^{2} = sum_{i = 0}^{2005}(b_{i} + 1)^{2} = sum_{i = 0}^{2005}(b_{i}^{2} + 2b_{i} + 1)]$ So $[sum_{i = 0}^{2005}b_{i} = frac {b_{2006}^{2} - 2006}2]$ Now $[sum_{i = 1}^{2006}b_{i} = frac {b_{2006}^{2} + 2b_{2006} - 2006}2]$ Therefore $[left|sum_{i = 1}^{2006}b_{i}right| = left|frac {(b_{2006} + 1)^{2} - 2007}2right|geq frac {2025 - 2007}{2} = 9]$ So $[left|sum_{i = 1}^{2006}x_{i}right|geq 27]$ First, we state that iff $x_{i - 1}ge0$ , $|x_i| = |x_{i - 1}| + 3$ and iff $x_{i - 1} < 0$ , $|x_i| = |x_{i - 1}| - 3$ . Now suppose $x_i = x_j$ for some $0le i < jle2006$ . Now, this means that $|x_i| = |x_j|$ , and so the number of positive numbers in the set ${x_i,x_{i + 1},ldots,x_{j - 1}}$ equals the number of negative numbers. Now pair the numbers in this list up in the following way: Whenever a positive and a negative number are adjacent in this progression, pair them up and remove them from this list. We claim that every pair will sum to -3.If the positive number comes first, then the negative number will have a magnitude three greater, so this is true. If the negative number comes first, then the positive number will have magnitude three smaller, and this will also be true. Now let us examine what happens when we remove those two from the sequence. WLOG, let the numbers be $x_k$ and $x_{k + 1}$ . Since one is positive and the other is negative, $|x_{k + 2}| = |x_{k + 1}|pm3 = |x_k|pm3mp3 = |x_k| = |x_{k - 1} + 3|$ . So the new sequence works under the same criteria as the old one. In this way, we can pair all of the numbers up in this subsequence so the sums of the pairs are -3. Thus, the average of these numbers will be -3/2 for all subsequences that start and end with the same number (not including one of those).Now, take all of the repeating subsequences out of the original sequence. The only thing that will be left will be a sequence ${0,3,6,9,cdots,3k}$ for some even $k$ . Since we started with 2006 terms, we removed $2006 - k$ (an even number) with an average of -3/2. Thus, the sum of both this remaining sequence and the removed stuff is $(2006 - k)( - 3/2) + sum_{i = 1}^k3k = (3/2)(k - 2006 + k(k + 1)) = 3/2(k^2 + 2k - 2006)$ . This must be minimized, so we find the roots: $k^2 + 2k = 2006implies (k + 1)^2 = 2007$ and $44^2 = 1936 < 2007 < 2025 = 45^2$ . Plugging in $k = 44$ yields $(3/2)(2025 - 2007) = 27$ (and $k = 42$ yields $- 237$ , a worse result). Thus, $fbox{27}$ is the closest to zero this sum can get.We know $|x_k| = |x_{k - 1} + 3|$ . We get rid of the absolute value by squaring both sides: ${x_k}^2 = {x_{k - 1}}^2 + 6{x_{k - 1}} + 9Rightarrow {x_k}^2 - {x_{k - 1}}^2 = 6{x_{k - 1}} + 9$ . 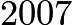So we set this up: $begin{align*} {x_1}^2 - {x_0}^2 & = 6{x_0} + 9 {x_2}^2 - {x_1}^2 & = 6{x_1} + 9 & vdots {x_{2007}}^2 - {x_{2006}}^2 & = 6{x_{2006}} + 9 end{align*}$ There are $2007$ equations. Sum them. We get: ${x_{2007}}^2 = 6left(x_1 + x_2 + cdots + x_{2006}right) + 9cdot{2007}$ So $|x_1 + x_2 + cdots + x_{2006}| = frac {left|{x_{2007}}^2 - 9cdot{2007}right|}{6}$
We know $3 | x_{2007}$ and we want to minimize $left|{x_{2007}}^2 - 9cdot{2007}right|$ , so $x_{2007}$ must be $3cdot{45}$ for it to be minimal ( $45^2 = 2025$ which is closest to $2007$ ).

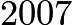This means that $|x_1 + x_2 + cdots + x_{2006}| = left|frac {9(2025 - 2007)}{6}right| = boxed{27}$