- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2007AIME II真题及答案解析
2007AIME II真题及答案解析
答案解析请参考文末
Problem 1
A mathematical organization is producing a set of commemorative license plates. Each plate contains a sequence of five characters chosen from the four letters in AIME and the four digits in ![]() . No character may appear in a sequence more times than it appears among the four letters in AIME or the four digits in
. No character may appear in a sequence more times than it appears among the four letters in AIME or the four digits in ![]() . A set of plates in which each possible sequence appears exactly once contains N license plates. Find N/10.
. A set of plates in which each possible sequence appears exactly once contains N license plates. Find N/10.
Problem 2
Find the number of ordered triples ![]() where
where ![]() ,
, ![]() , and
, and ![]() are positive integers,
are positive integers, ![]() is a factor of
is a factor of ![]() ,
, ![]() is a factor of
is a factor of ![]() , and
, and ![]() .
.
Problem 3
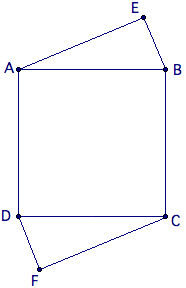
Square ![]() has side length
has side length ![]() , and points
, and points ![]() and
and ![]() are exterior to the square such that
are exterior to the square such that ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 4
The workers in a factory produce widgets and whoosits. For each product, production time is constant and identical for all workers, but not necessarily equal for the two products. In one hour, ![]() workers can produce
workers can produce ![]() widgets and
widgets and ![]() whoosits. In two hours,
whoosits. In two hours, ![]() workers can produce
workers can produce ![]() widgets and
widgets and ![]() whoosits. In three hours,
whoosits. In three hours, ![]() workers can produce
workers can produce ![]() widgets and
widgets and ![]() whoosits. Find
whoosits. Find ![]() .
.
Problem 5
The graph of the equation ![]() is drawn on graph paper with each square representing one unit in each direction. How many of the
is drawn on graph paper with each square representing one unit in each direction. How many of the ![]() by
by ![]() graph paper squares have interiors lying entirely below the graph and entirely in the first quadrant?
graph paper squares have interiors lying entirely below the graph and entirely in the first quadrant?
Problem 6
An integer is called parity-monotonic if its decimal representation ![]() satisfies
satisfies ![]() if
if ![]() is odd, and
is odd, and ![]() if
if ![]() is even. How many four-digit parity-monotonic integers are there?
is even. How many four-digit parity-monotonic integers are there?
Problem 7
Given a real number ![]() let
let ![]() denote the greatest integer less than or equal to
denote the greatest integer less than or equal to ![]() For a certain integer
For a certain integer ![]() there are exactly
there are exactly ![]() positive integers
positive integers ![]() such that
such that ![]() and
and ![]() divides
divides ![]() for all
for all ![]() such that
such that ![]()
Find the maximum value of ![]() for
for ![]()
Problem 8
A rectangular piece of paper measures 4 units by 5 units. Several lines are drawn parallel to the edges of the paper. A rectangle determined by the intersections of some of these lines is called basic if
(i) all four sides of the rectangle are segments of drawn line segments, and
(ii) no segments of drawn lines lie inside the rectangle.
Given that the total length of all lines drawn is exactly 2007 units, let ![]() be the maximum possible number of basic rectangles determined. Find the remainder when
be the maximum possible number of basic rectangles determined. Find the remainder when ![]() is divided by 1000.
is divided by 1000.
Problem 9
Rectangle ![]() is given with
is given with ![]() and
and ![]() Points
Points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() respectively, such that
respectively, such that ![]() The inscribed circle of triangle
The inscribed circle of triangle ![]() is tangent to
is tangent to ![]() at point
at point ![]() and the inscribed circle of triangle
and the inscribed circle of triangle ![]() is tangent to
is tangent to ![]() at point
at point ![]() Find
Find ![]()
Problem 10
Let ![]() be a set with six elements. Let
be a set with six elements. Let ![]() be the set of all subsets of
be the set of all subsets of ![]() Subsets
Subsets ![]() and
and ![]() of
of ![]() , not necessarily distinct, are chosen independently and at random from
, not necessarily distinct, are chosen independently and at random from ![]() . The probability that
. The probability that ![]() is contained in at least one of
is contained in at least one of ![]() or
or ![]() is
is ![]() where
where ![]() ,
, ![]() , and
, and ![]() are positive integers,
are positive integers, ![]() is prime, and
is prime, and ![]() and
and ![]() are relatively prime. Find
are relatively prime. Find ![]() (The set
(The set ![]() is the set of all elements of
is the set of all elements of ![]() which are not in
which are not in ![]() )
)
Problem 11
Two long cylindrical tubes of the same length but different diameters lie parallel to each other on a flat surface. The larger tube has radius ![]() and rolls along the surface toward the smaller tube, which has radius
and rolls along the surface toward the smaller tube, which has radius ![]() . It rolls over the smaller tube and continues rolling along the flat surface until it comes to rest on the same point of its circumference as it started, having made one complete revolution. If the smaller tube never moves, and the rolling occurs with no slipping, the larger tube ends up a distance
. It rolls over the smaller tube and continues rolling along the flat surface until it comes to rest on the same point of its circumference as it started, having made one complete revolution. If the smaller tube never moves, and the rolling occurs with no slipping, the larger tube ends up a distance ![]() from where it starts. The distance
from where it starts. The distance ![]() can be expressed in the form
can be expressed in the form ![]() where
where ![]()
![]() and
and ![]() are integers and
are integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
Problem 12
The increasing geometric sequence ![]() consists entirely of integral powers of
consists entirely of integral powers of ![]() Given that
Given that
 and
and 
find ![]()
Problem 13
A triangular array of squares has one square in the first row, two in the second, and in general, ![]() squares in the
squares in the ![]() th row for
th row for ![]() With the exception of the bottom row, each square rests on two squares in the row immediately below (illustrated in given diagram). In each square of the eleventh row, a
With the exception of the bottom row, each square rests on two squares in the row immediately below (illustrated in given diagram). In each square of the eleventh row, a ![]() or a
or a ![]() is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of
is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of ![]() 's and
's and ![]() 's in the bottom row is the number in the top square a multiple of
's in the bottom row is the number in the top square a multiple of ![]() ?
?
![[asy] for (int i=0; i<12; ++i){ for (int j=0; j<i; ++j){ //dot((-j+i/2,-i)); draw((-j+i/2,-i)--(-j+i/2+1,-i)--(-j+i/2+1,-i+1)--(-j+i/2,-i+1)--cycle); } } [/asy]](https://latex.artofproblemsolving.com/f/4/8/f482d8c340a42e4beffcdc4a965cff94810d48fc.png)
Problem 14
Let ![]() be a polynomial with real coefficients such that
be a polynomial with real coefficients such that ![]()
![]() and for all
and for all ![]() ,
, ![]() Find
Find ![]()
Problem 15
Four circles ![]()
![]()
![]() and
and ![]() with the same radius are drawn in the interior of triangle
with the same radius are drawn in the interior of triangle ![]() such that
such that ![]() is tangent to sides
is tangent to sides ![]() and
and ![]() ,
, ![]() to
to ![]() and
and ![]() ,
, ![]() to
to ![]() and
and ![]() , and
, and ![]() is externally tangent to
is externally tangent to ![]()
![]() and
and ![]() . If the sides of triangle
. If the sides of triangle ![]() are
are ![]()
![]() and
and ![]() the radius of
the radius of ![]() can be represented in the form
can be represented in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
2007AIME II详细解析
- There are 7 different characters that can be picked, with 0 being the only number that can be repeated twice.
- If
 appears 0 or 1 times amongst the sequence, there are
appears 0 or 1 times amongst the sequence, there are  sequences possible.
sequences possible. - If
 appears twice in the sequence, there are
appears twice in the sequence, there are  places to place the
places to place the  s. There are
s. There are  ways to place the remaining three characters. Totally, that gives us
ways to place the remaining three characters. Totally, that gives us  .
.
Thus,
 , and
, and  .
. - If
- Denote
 and
and  . The last condition reduces to
. The last condition reduces to  . Therefore,
. Therefore,  is equal to one of the 9 factors of
is equal to one of the 9 factors of  .Subtracting the one, we see that
.Subtracting the one, we see that  . There are exactly
. There are exactly  ways to find pairs of
ways to find pairs of  if
if  . Thus, there are
. Thus, there are  solutions of
solutions of  .Alternatively, note that the sum of the divisors of
.Alternatively, note that the sum of the divisors of  is
is  (notice that after distributing, every divisor is accounted for). This evaluates to
(notice that after distributing, every divisor is accounted for). This evaluates to  . Subtract
. Subtract  for reasons noted above to get
for reasons noted above to get  . Finally, this changes
. Finally, this changes  , so we have to add one to account for that. We get
, so we have to add one to account for that. We get  .
. -
Solution 1
Let
 , so that
, so that  . By the diagonal,
. By the diagonal,  .
.The sum of the squares of the sides of a parallelogram is the sum of the squares of the diagonals.
![[EF^2 = 2cdot(5^2 + 433) - 338 = 578.]](https://latex.artofproblemsolving.com/2/f/f/2ff9c1e6d8c42d54ddd5fd5c2bb27a7e88c2b201.png)
Solution 2
Extend
 and
and  to their points of intersection. Since
to their points of intersection. Since  and are both
and are both  right triangles, we can come to the conclusion that the two new triangles are also congruent to these two (use ASA, as we know all the sides are
right triangles, we can come to the conclusion that the two new triangles are also congruent to these two (use ASA, as we know all the sides are  and the angles are mostly complementary). Thus, we create a square with sides
and the angles are mostly complementary). Thus, we create a square with sides  .
.![[asy]unitsize(0.25 cm); pair A, B, C, D, E, F, G, H; A = (0,13); B = (13,13); C = (13,0); D = (0,0); E = A + (12*12/13,5*12/13); F = D + (5*5/13,-5*12/13); G = rotate(90,(A + C)/2)*(E); H = rotate(90,(A + C)/2)*(F); draw(A--B--C--D--cycle); draw(E--G--F--H--cycle); dot("$A$", A, N); dot("$B$", B, dir(0)); dot("$C$", C, S); dot("$D$", D, W); dot("$E$", E, N); dot("$F$", F, S); dot("$G$", G, W); dot("$H$", H, dir(0));[/asy]](https://latex.artofproblemsolving.com/c/d/7/cd75b0b5f2740c3766ea40dc5063e2381c70c247.png)
 is the diagonal of the square, with length
is the diagonal of the square, with length  ; the answer is
; the answer is  .
. - Suppose that it takes
 hours for one worker to create one widget, and
hours for one worker to create one widget, and  hours for one worker to create one whoosit.Therefore, we can write that (note that two hours is similar to having twice the number of workers, and so on):
hours for one worker to create one whoosit.Therefore, we can write that (note that two hours is similar to having twice the number of workers, and so on):



Solve the system of equations with the first two equations to find that
 . Substitute this into the third equation to find that
. Substitute this into the third equation to find that  , so
, so  .
. -
Solution 1
There are
 squares in total formed by the rectangle with edges on the x and y axes and with vertices on the intercepts of the equation, since the intercepts of the lines are
squares in total formed by the rectangle with edges on the x and y axes and with vertices on the intercepts of the equation, since the intercepts of the lines are  .
.Count the number of squares that the diagonal of the rectangle passes through. Since the two diagonals of a rectangle are congruent, we can consider instead the diagonal
 . This passes through 8 horizontal lines (
. This passes through 8 horizontal lines ( ) and 222 vertical lines (
) and 222 vertical lines ( ). At every time we cross a line, we enter a new square. Since 9 and 223 are relatively prime, we don’t have to worry about crossing an intersection of a horizontal and vertical line at one time. We must also account for the first square. This means that it passes through
). At every time we cross a line, we enter a new square. Since 9 and 223 are relatively prime, we don’t have to worry about crossing an intersection of a horizontal and vertical line at one time. We must also account for the first square. This means that it passes through  squares.
squares.The number of non-diagonal squares is
 . Divide this in 2 to get the number of squares in one of the triangles, with the answer being
. Divide this in 2 to get the number of squares in one of the triangles, with the answer being  .
.Solution 2
Count the number of each squares in each row of the triangle. The intercepts of the line are
 .
.In the top row, there clearly are no squares that can be formed. In the second row, we see that the line
 gives a
gives a  value of
value of  , which means that
, which means that  unit squares can fit in that row. In general, there are
unit squares can fit in that row. In general, there are
triangles. Since
 , we see that there are more than
, we see that there are more than  triangles. Now, count the fractional parts.
triangles. Now, count the fractional parts. 

 . Adding them up, we get
. Adding them up, we get  .
.Solution 3
From Pick's Theorem,
 . In other words,
. In other words,  and I is
and I is  .
.Do you see why we simply set
 as the answer as well? That's because every interior point, if moved down and left one (southwest direction), can have that point and the previous point create a unit square. For example,
as the answer as well? That's because every interior point, if moved down and left one (southwest direction), can have that point and the previous point create a unit square. For example,  moves to
moves to  , so the square of points
, so the square of points  is one example. This applies, of course, for
is one example. This applies, of course, for  points.
points.Solution 4
We know that the number of squares intersected in an
 rectangle is
rectangle is  . So if we apply that here, we get that the number of intersected squares is:
. So if we apply that here, we get that the number of intersected squares is: .
.Now just subtract that from the total number of squares and divide by 2, since we want the number of squares below the line.
So,

- Let's set up a table of values. Notice that 0 and 9 both cannot appear as any of
 because of the given conditions. A clear pattern emerges.For example, for
because of the given conditions. A clear pattern emerges.For example, for  in the second column, we note that
in the second column, we note that  is less than
is less than  , but greater than
, but greater than  , so there are four possible places to align
, so there are four possible places to align  as the second digit.
as the second digit.
Digit 1st 2nd 3rd 4th 0 0 0 0 64 1 1 4 16 64 2 1 4 16 64 3 1 4 16 64 4 1 4 16 64 5 1 4 16 64 6 1 4 16 64 7 1 4 16 64 8 1 4 16 64 9 0 0 0 64 This problem can be solved via recursion since we are "building a string" of numbers with some condition. We want to create a new string by adding a new digit at the front so we avoid complications(
 can't be at the front and do digit is less than
can't be at the front and do digit is less than  ). There are
). There are  options to add no matter what(try some examples if you want) so the recursion is
options to add no matter what(try some examples if you want) so the recursion is  where
where  stands for the number of such numbers with
stands for the number of such numbers with  digits. Since
digits. Since  the answer is
the answer is  .
.For any number from 1-8, there are exactly 4 numbers from 1-8 that are odd and less than the number or that are even and greater than the number (the same will happen for 0 and 9 in the last column). Thus, the answer is
 .
. - For
 , we see that
, we see that ![$sqrt[3]{1} ldots sqrt[3]{7}$](https://latex.artofproblemsolving.com/9/3/3/9339e15771e9f6fd053bad1f11137bcb1e576985.png) all work, giving 7 integers. For
all work, giving 7 integers. For  , we see that in
, we see that in ![$sqrt[3]{8} ldots sqrt[3]{26}$](https://latex.artofproblemsolving.com/0/b/1/0b1b2a0bb4dfe13cdca56c74fc2872c55cc07fc7.png) , all of the even numbers work, giving 10 integers. For
, all of the even numbers work, giving 10 integers. For  , we get 13, and so on. We can predict that at
, we get 13, and so on. We can predict that at  we get 70.To prove this, note that all of the numbers from
we get 70.To prove this, note that all of the numbers from ![$sqrt[3]{x^3} ldots sqrt[3]{(x+1)^3 - 1}$](https://latex.artofproblemsolving.com/d/d/4/dd4c7646f276f40c0128e3ad6cdc26603f11629c.png) divisible by
divisible by  work. Thus,
work. Thus,  (the one to be inclusive) integers will fit the conditions.
(the one to be inclusive) integers will fit the conditions.  .The maximum value of
.The maximum value of  . Therefore, the solution is
. Therefore, the solution is  .Obviously
.Obviously  is positive. Then, we can let
is positive. Then, we can let  equal
equal  and similarly let
and similarly let  equal
equal  .The wording of this problem (which uses "exactly") tells us that
.The wording of this problem (which uses "exactly") tells us that  . Taking away
. Taking away  from our inequality results in
from our inequality results in  . Since
. Since  ,
,  , and
, and  are all integers, this inequality is equivalent to
are all integers, this inequality is equivalent to  . Since
. Since  is positive, we can divide the inequality by
is positive, we can divide the inequality by  to get
to get  . Clearly the only
. Clearly the only  that satisfies is
that satisfies is  .Then,
.Then,  is the maximum value of
is the maximum value of  . (Remember we set
. (Remember we set  equal to
equal to  !)
!) - Denote the number of horizontal lines as
 , and the number of vertical lines as
, and the number of vertical lines as  . The number of basic rectangles is
. The number of basic rectangles is  .
.  . Substituting, we find that
. Substituting, we find that  .FOIL this to get a quadratic,
.FOIL this to get a quadratic,  . Use
. Use  to find the maximum possible value of the quadratic:
to find the maximum possible value of the quadratic:  . However, this gives a non-integral answer for
. However, this gives a non-integral answer for  . The closest two values that work are
. The closest two values that work are  and
and  .We see that
.We see that  . The solution is
. The solution is  .We realize that drawing
.We realize that drawing  vertical lines and
vertical lines and  horizontal lines, the number of basic rectangles we have is
horizontal lines, the number of basic rectangles we have is  . The easiest possible case to see is
. The easiest possible case to see is  vertical and
vertical and  horizontal lines, as
horizontal lines, as  . Now, for every 4 vertical lines you take away, you can add 5 horizontal lines, so you basically have the equation
. Now, for every 4 vertical lines you take away, you can add 5 horizontal lines, so you basically have the equation  maximize.Expanded, this gives
maximize.Expanded, this gives  . From
. From  you get that the vertex is at
you get that the vertex is at  . This is not an integer though, so you see that when
. This is not an integer though, so you see that when  , you have
, you have  and that when x=6, you have
and that when x=6, you have  .
.  , so the maximum integral value for x occurs when
, so the maximum integral value for x occurs when  . Now you just evaluate
. Now you just evaluate  which is
which is  .
. - Several Pythagorean triples exist amongst the numbers given.
 . Also, the length of
. Also, the length of  .Use the Two Tangent Theorem on
.Use the Two Tangent Theorem on  . Since both circles are inscribed in congruent triangles, they are congruent; therefore,
. Since both circles are inscribed in congruent triangles, they are congruent; therefore,  . By the Two Tangent theorem, note that
. By the Two Tangent theorem, note that  , making
, making ![$BX = 105 - EX = 105 - left[frac{287 - PQ}{2}right]$](https://latex.artofproblemsolving.com/9/4/a/94aa6477b6e4192a9abb21ead4f1df4fc8ac1c9a.png) . Also,
. Also,  .
. ![$FY = 364 - BY = 364 - left[105 - left[frac{287 - PQ}{2}right]right]$](https://latex.artofproblemsolving.com/8/1/b/81be43588a7de527d3104d0a31c9db9ed3bb957c.png) .Finally,
.Finally, ![$FP = FY = 364 - left[105 - left[frac{287 - PQ}{2}right]right] = frac{805 - PQ}{2}$](https://latex.artofproblemsolving.com/a/a/8/aa8b22fe1e485aa4ffa1e7863cd44c711d9c744a.png) . Also,
. Also,  . Equating, we see that
. Equating, we see that  , so
, so  .By the Two Tangent Theorem, we have that
.By the Two Tangent Theorem, we have that  . Solve for
. Solve for  . Also,
. Also,  , so
, so  . Since
. Since  , this can become
, this can become 
 . Substituting in their values, the answer is
. Substituting in their values, the answer is  .Call the incenter of
.Call the incenter of 
 and the incenter of
and the incenter of 
 . Draw triangles
. Draw triangles  .Drawing
.Drawing  , We find that
, We find that  . Applying the same thing for
. Applying the same thing for  , we find that
, we find that  as well. Draw a line through
as well. Draw a line through  parallel to the sides of the rectangle, to intersect the opposite side at
parallel to the sides of the rectangle, to intersect the opposite side at  respectively. Drawing
respectively. Drawing  and
and  , we can find that
, we can find that  . We then use Heron's formula to get:
. We then use Heron's formula to get:![[[BEF] = [DEF] = 11 466]](https://latex.artofproblemsolving.com/3/2/0/320c635dd39969d1931a7ed56181c70ae4ce1202.png) .
.
So the inradius of the triangle-type things is
 .
.Now, we just have to find
 , which can be done with simple subtraction, and then we can use the Pythagorean Theorem to find
, which can be done with simple subtraction, and then we can use the Pythagorean Theorem to find  .
.Why not first divide everything by its greatest common factor,
 ? Then we're left with much simpler numbers which saves a lot of time. In the end, we will multiply by
? Then we're left with much simpler numbers which saves a lot of time. In the end, we will multiply by  .
.From there, we draw the same diagram as above (with smaller numbers). We soon find that the longest side of both triangles is 52 (64 - 12). That means:
 indicating
indicating  so
so  .
.Now, we can start applying the equivalent tangents. Calling them
 ,
,  , and
, and  (with
(with  being the longest and a being the shortest),
being the longest and a being the shortest), is the semi perimeter or
is the semi perimeter or  . And since the longest side (which has
. And since the longest side (which has  ) is
) is  ,
,  .
.Note that the distance
 we desired to find is just
we desired to find is just  . What is
. What is  then?
then?  . And
. And  is
is  . Therefore the answer is
. Therefore the answer is  ...
... 
Multiply by
 back again (I hope you remembered to write this in
back again (I hope you remembered to write this in  letters on top of the scrap paper!), we actually get
letters on top of the scrap paper!), we actually get  .
. - Use casework:
 has 6 elements:
has 6 elements:
- Probability:

 must have either 0 or 6 elements, probability:
must have either 0 or 6 elements, probability: 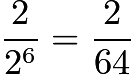 .
.
- Probability:
 has 5 elements:
has 5 elements:
- Probability:

 must have either 0, 6, or 1, 5 elements. The total probability is
must have either 0, 6, or 1, 5 elements. The total probability is  .
.
- Probability:
 has 4 elements:
has 4 elements:
- Probability:

 must have either 0, 6; 1, 5; or 2,4 elements. If there are 1 or 5 elements, the set which contains 5 elements must have four emcompassing
must have either 0, 6; 1, 5; or 2,4 elements. If there are 1 or 5 elements, the set which contains 5 elements must have four emcompassing  and a fifth element out of the remaining
and a fifth element out of the remaining  numbers. The total probability is
numbers. The total probability is  .
.
- Probability:
We could just continue our casework. In general, the probability of picking B with
 elements is
elements is  . Since the sum of the elements in the
. Since the sum of the elements in the  th row of Pascal's Triangle is
th row of Pascal's Triangle is  , the probability of obtaining
, the probability of obtaining  or
or  which encompasses
which encompasses  is
is  . In addition, we must count for when
. In addition, we must count for when  is the empty set (probability:
is the empty set (probability:  ), of which all sets of
), of which all sets of  will work (probability:
will work (probability:  ).
).Thus, the solution we are looking for is



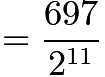 .
.The answer is
 .
.we need
 to be a subset of
to be a subset of  or
or  we can divide each element of
we can divide each element of  into 4 categories:
into 4 categories:- it is in
 and
and 
- it is in
 but not in
but not in 
- it is not in
 but is in
but is in 
- or it is not in
 and not in
and not in 
these can be denoted as
 ,
,  ,
, , and
, and 
we note that if all of the elements are in
 ,
,  or
or  we have that
we have that  is a subset of
is a subset of  which can happen in
which can happen in  ways
wayssimilarly if the elements are in
 ,
, , or
, or  we have that
we have that  is a subset of
is a subset of  which can happen in
which can happen in  ways as well
ways as wellbut we need to make sure we don't over-count ways that are in both sets these are when
 or
or  which can happen in
which can happen in  ways so our probability is
ways so our probability is  .
.so the final answer is
 .
. must be in
must be in  or
or  must be in
must be in  . This is equivalent to saying that
. This is equivalent to saying that  must be in
must be in  or
or  is disjoint from
is disjoint from  . The probability of this is the sum of the probabilities of each event individually minus the probability of each event occurring simultaneously. There are 6C
. The probability of this is the sum of the probabilities of each event individually minus the probability of each event occurring simultaneously. There are 6C ways to choose
ways to choose  , where
, where  is the number of elements in
is the number of elements in  . From those
. From those  elements, there are
elements, there are  ways to choose
ways to choose  . Thus, the probability that
. Thus, the probability that  is in
is in  is the sum of all the values
is the sum of all the values  for values of
for values of  ranging from
ranging from  to
to  . For the second probability, the ways to choose
. For the second probability, the ways to choose  stays the same but the ways to choose
stays the same but the ways to choose  is now
is now ![${2^[6-x]}$](https://latex.artofproblemsolving.com/0/f/6/0f6929ef3a095af07a74b55224c54553b8a5a86d.png) . We see that these two summations are simply from the Binomial Theorem and that each of them is
. We see that these two summations are simply from the Binomial Theorem and that each of them is  . We subtract the case where both of them are true. This only happens when
. We subtract the case where both of them are true. This only happens when  is the null set.
is the null set.  can be any subset of
can be any subset of  , so there are
, so there are  possibilities. Our final sum of possibilities is
possibilities. Our final sum of possibilities is  . We have
. We have  total possibilities for both
total possibilities for both  and
and  , so there are
, so there are  total possibilities.
total possibilities.  . This reduces down to
. This reduces down to  . The answer is thus
. The answer is thus  .
.Let
 denote the number of elements in a general set
denote the number of elements in a general set  . We use complementary counting.
. We use complementary counting.There is a total of
 elements in
elements in  , so the total number of ways to choose
, so the total number of ways to choose  and
and  is
is  .
.Note that the number of
 -element subset of
-element subset of  is
is  . In general, for
. In general, for  , in order for
, in order for  to be in neither
to be in neither  nor
nor  ,
,  must have at least one element from both
must have at least one element from both  and
and  . In other words,
. In other words,  must contain any subset of
must contain any subset of  and
and  except for the empty set
except for the empty set  . This can be done in
. This can be done in  ways. As
ways. As  ranges from
ranges from  to
to  , we can calculate the total number of unsuccessful outcomes to be
, we can calculate the total number of unsuccessful outcomes to be![[sum_{|A| = 0}^{6} binom{6}{|A|} (2^{|A|} - 1)(2^{6-|A|} - 1) = 2702.]](https://latex.artofproblemsolving.com/3/b/2/3b2f6cf7e272f682a2c9f67e44c53f0d5287602f.png) So our desired answer is
So our desired answer is![[1 - dfrac{2702}{2^{12}} = dfrac{697}{2^{11}} Rightarrow boxed{710}.]](https://latex.artofproblemsolving.com/5/a/c/5ac3f204b3763f4d516ef0abc2bdedeb663c9398.png)
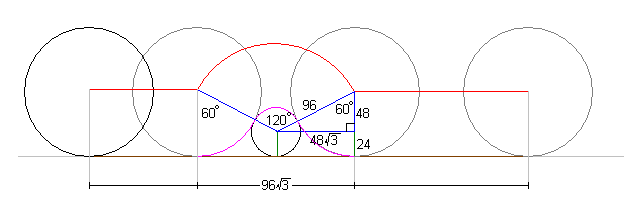 If it weren’t for the small tube, the larger tube would travel
If it weren’t for the small tube, the larger tube would travel  . Consider the distance from which the larger tube first contacts the smaller tube, until when it completely loses contact with the smaller tube.Drawing the radii as shown in the diagram, notice that the hypotenuse of the right triangle in the diagram has a length of
. Consider the distance from which the larger tube first contacts the smaller tube, until when it completely loses contact with the smaller tube.Drawing the radii as shown in the diagram, notice that the hypotenuse of the right triangle in the diagram has a length of  . The horizontal line divides the radius of the larger circle into
. The horizontal line divides the radius of the larger circle into  on the top half, which indicates that the right triangle has leg of 48 and hypotenuse of 96, a
on the top half, which indicates that the right triangle has leg of 48 and hypotenuse of 96, a  .Find the length of the purple arc in the diagram (the distance the tube rolled, but not the horizontal distance). The sixty degree central angle indicates to take
.Find the length of the purple arc in the diagram (the distance the tube rolled, but not the horizontal distance). The sixty degree central angle indicates to take  of the circumference of the larger circle (twice), while the
of the circumference of the larger circle (twice), while the  central angle in the smaller circle indicates to take
central angle in the smaller circle indicates to take  of the circumference. This adds up to
of the circumference. This adds up to  .The actual horizontal distance it takes can be found by using the
.The actual horizontal distance it takes can be found by using the  s. The missing leg is equal in length to
s. The missing leg is equal in length to  . Thus, the total horizontal distance covered is
. Thus, the total horizontal distance covered is  .Thus, we get
.Thus, we get  , and our answer is
, and our answer is  .
.- Suppose that
 , and that the common ratio between the terms is
, and that the common ratio between the terms is  .The first conditions tells us that
.The first conditions tells us that  . Using the rules of logarithms, we can simplify that to
. Using the rules of logarithms, we can simplify that to  . Thus,
. Thus,  . Since all of the terms of the geometric sequence are integral powers of
. Since all of the terms of the geometric sequence are integral powers of  , we know that both
, we know that both  and
and  must be powers of 3. Denote
must be powers of 3. Denote  and
and  . We find that
. We find that  . The possible positive integral pairs of
. The possible positive integral pairs of  are
are  .The second condition tells us that
.The second condition tells us that  . Using the sum formula for a geometric series and substituting
. Using the sum formula for a geometric series and substituting  and
and  , this simplifies to
, this simplifies to  . The fractional part
. The fractional part  . Thus, we need
. Thus, we need  . Checking the pairs above, only
. Checking the pairs above, only  is close.Our solution is therefore
is close.Our solution is therefore  .All these integral powers of
.All these integral powers of  are all different, thus in base
are all different, thus in base  the sum of these powers would consist of
the sum of these powers would consist of  s and
s and  s. Thus the largest value
s. Thus the largest value  must be
must be  in order to preserve the givens. Then we find by the given that
in order to preserve the givens. Then we find by the given that  , and we know that the exponents of
, and we know that the exponents of  are in an arithmetic sequence. Thus
are in an arithmetic sequence. Thus  , and
, and  . Thus
. Thus  .
. - Label each of the bottom squares as
 .Through induction, we can find that the top square is equal to
.Through induction, we can find that the top square is equal to  . (This also makes sense based on a combinatorial argument: the number of ways a number can "travel" to the top position going only up is equal to the number of times it will be counted in the final sum.)Examine the equation
. (This also makes sense based on a combinatorial argument: the number of ways a number can "travel" to the top position going only up is equal to the number of times it will be counted in the final sum.)Examine the equation  . All of the coefficients from
. All of the coefficients from  will be multiples of
will be multiples of  (since the numerator will have a
(since the numerator will have a  ). Thus, the expression boils down to
). Thus, the expression boils down to  . Reduce to find that
. Reduce to find that  . Out of
. Out of  , either all are equal to
, either all are equal to  , or three of them are equal to
, or three of them are equal to  . This gives
. This gives  possible combinations of numbers that work.The seven terms from
possible combinations of numbers that work.The seven terms from  can assume either
can assume either  or
or  , giving us
, giving us  possibilities. The answer is therefore
possibilities. The answer is therefore  .
. - Let
 be a root of
be a root of  . Then we have
. Then we have  ; since
; since  is a root, we have
is a root, we have  ; therefore
; therefore  is also a root. Thus, if
is also a root. Thus, if  is real and non-zero,
is real and non-zero,  , so
, so  has infinitely many roots. Since
has infinitely many roots. Since  is a polynomial (thus of finite degree) and
is a polynomial (thus of finite degree) and  is nonzero,
is nonzero,  has no real roots.Note that
has no real roots.Note that  is not constant. We then find two complex roots:
is not constant. We then find two complex roots:  . We find that
. We find that  , and that
, and that  . This means that
. This means that  . Thus,
. Thus,  are roots of the polynomial, and so
are roots of the polynomial, and so  will be a factor of the polynomial. (Note: This requires the assumption that
will be a factor of the polynomial. (Note: This requires the assumption that  . Clearly,
. Clearly,  , because that would imply the existence of a real root.)The polynomial is thus in the form of
, because that would imply the existence of a real root.)The polynomial is thus in the form of  . Substituting into the given expression, we have
. Substituting into the given expression, we have![[(x^2+1)g(x)(4x^4+1)g(2x^2)=((2x^3+x)^2+1)g(2x^3+x)]](https://latex.artofproblemsolving.com/8/7/5/875a63c1137f6b1ca6ace78c6d53bd157c06da32.png)
![[(4x^6+4x^4+x^2+1)g(x)g(2x^2)=(4x^6+4x^4+x^2+1)g(2x^3+x)]](https://latex.artofproblemsolving.com/2/0/7/207345bb37890021060af3b78232dd1da626d356.png) Thus either
Thus either  is 0 for any
is 0 for any  , or
, or  satisfies the same constraints as
satisfies the same constraints as  . Continuing, by infinite descent,
. Continuing, by infinite descent,  for some
for some  .Since
.Since  for some
for some  , we have
, we have  ; so
; so  .Comment: The answer is clearly correct, but the proof has a gap, i.e. there is no reason that
.Comment: The answer is clearly correct, but the proof has a gap, i.e. there is no reason that  . Since
. Since  has no real roots, the degree must be even. Consider
has no real roots, the degree must be even. Consider  . Then since
. Then since  is non-zero,
is non-zero,  . Now the function
. Now the function  applied repeatedly from some real starting value of x becomes arbitrarily large, and the limit of
applied repeatedly from some real starting value of x becomes arbitrarily large, and the limit of  as
as  approaches infinity is 1, so
approaches infinity is 1, so  =1 for all x, or
=1 for all x, or  . Then
. Then  for some polynomial
for some polynomial  , and
, and  . Now suppose h has degree m. It is clearly monic. Assume that the next highest non-zero coefficient in h is k. Then, subtracting
. Now suppose h has degree m. It is clearly monic. Assume that the next highest non-zero coefficient in h is k. Then, subtracting  from both sides of the equation yields a polynomial equality with degree
from both sides of the equation yields a polynomial equality with degree  on the left and degree
on the left and degree  on the right, a contradiction. So
on the right, a contradiction. So  , and
, and  .
. - First, apply Heron's formula to find that the area is
 . Also the semiperimeter is
. Also the semiperimeter is  . So the inradius is
. So the inradius is  .Now consider the incenter I. Let the radius of one of the small circles be
.Now consider the incenter I. Let the radius of one of the small circles be  . Let the centers of the three little circles tangent to the sides of
. Let the centers of the three little circles tangent to the sides of  be
be  ,
,  , and
, and  . Let the centre of the circle tangent to those three circles be P. A homothety centered at
. Let the centre of the circle tangent to those three circles be P. A homothety centered at  takes
takes  to
to  with factor
with factor  . The same homothety takes
. The same homothety takes  to the circumcentre of
to the circumcentre of  , so
, so  , where
, where  is the circumradius of
is the circumradius of  . The circumradius of
. The circumradius of  can be easily computed by
can be easily computed by  , so doing that reveals
, so doing that reveals  . Then
. Then  , so the answer is
, so the answer is  .
. Consider a 13-14-15 triangle.
Consider a 13-14-15 triangle.  [By Heron's Formula or by 5-12-13 and 9-12-15 right triangles.]The inradius is
[By Heron's Formula or by 5-12-13 and 9-12-15 right triangles.]The inradius is  , where
, where  is the semiperimeter. Scale the triangle with the inradius by a linear scale factor,
is the semiperimeter. Scale the triangle with the inradius by a linear scale factor,  The circumradius is
The circumradius is  where
where 
 and
and  are the side-lengths. Scale the triangle with the circumradius by a linear scale factor,
are the side-lengths. Scale the triangle with the circumradius by a linear scale factor,  .Cut and combine the triangles, as shown. Then solve for 4u:
.Cut and combine the triangles, as shown. Then solve for 4u:
The solution is
 .
.
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









