Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2007AIME I真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月9日下午4:21

2007AIME I真题及答案解析

答案解析请参考文末

Problem 1

How many positive perfect squares less than $10^6$ are multiples of 24?

Problem 2

A 100 foot long moving walkway moves at a constant rate of 6 feet per second. Al steps onto the start of the walkway and stands. Bob steps onto the start of the walkway two seconds later and strolls forward along the walkway at a constant rate of 4 feet per second. Two seconds after that, Cy reaches the start of the walkway and walks briskly forward beside the walkway at a constant rate of 8 feet per second. At a certain time, one of these three persons is exactly halfway between the other two. At that time, find the distance in feet between the start of the walkway and the middle person.

Problem 3

The complex number $z$ is equal to $9+bi$ , where $b$ is a positive real number and $i^{2}=-1$ . Given that the imaginary parts of $z^{2}$ and $z^{3}$ are the same, what is $b$ equal to?

Problem 4

Three planets orbit a star circularly in the same plane. Each moves in the same direction and moves at constant speed. Their periods are $60$ , $84$ , and $140$ years. The three planets and the star are currently collinear. What is the fewest number of years from now that they will all be collinear again?

Problem 5

The formula for converting a Fahrenheit temperature $F$ to the corresponding Celsius temperature $C$ is $C = frac{5}{9}(F-32).$ An integer Fahrenheit temperature is converted to Celsius, rounded to the nearest integer, converted back to Fahrenheit, and again rounded to the nearest integer.

For how many integer Fahrenheit temperatures between $32$ and $1000$ inclusive does the original temperature equal the final temperature?

Problem 6

A frog is placed at the origin on the number line, and moves according to the following rule: in a given move, the frog advances to either the closest point with a greater integer coordinate that is a multiple of $3$ , or to the closest point with a greater integer coordinate that is a multiple of $13$ . A move sequence is a sequence of coordinates which correspond to valid moves, beginning with $0$ , and ending with $39$ . For example, $0, 3, 6, 13, 15, 26, 39$ is a move sequence. How many move sequences are possible for the frog?

Problem 7

Let $N = sum_{k = 1}^{1000} k ( lceil log_{sqrt{2}} k rceil - lfloor log_{sqrt{2}} k rfloor )$

Find the remainder when $N$ is divided by 1000. ( $lfloor{k}rfloor$ is the greatest integer less than or equal to $k$ , and $lceil{k}rceil$ is the least integer greater than or equal to $k$ .)

Problem 8

The polynomial $P(x)$ is cubic. What is the largest value of $k$ for which the polynomials $Q_1(x) = x^2 + (k-29)x - k$ and $Q_2(x) = 2x^2+ (2k-43)x + k$ are both factors of $P(x)$ ?

Problem 9

In right triangle $ABC$ with right angle $C$ , $CA = 30$ and $CB = 16$ . Its legs $CA$ and $CB$ are extended beyond $A$ and $B$ . Points $O_1$ and $O_2$ lie in the exterior of the triangle and are the centers of two circles with equal radii. The circle with center $O_1$ is tangent to the hypotenuse and to the extension of leg $CA$ , the circle with center $O_2$ is tangent to the hypotenuse and to the extension of leg $CB$ , and the circles are externally tangent to each other. The length of the radius of either circle can be expressed as $p/q$ , where $p$ and $q$ are relatively prime positive integers. Find $p+q$ .

AIME I 2007-9.png

Problem 10

In a $6 times 4$ grid ( $6$ rows, $4$ columns), $12$ of the $24$ squares are to be shaded so that there are two shaded squares in each row and three shaded squares in each column. Let $N$ be the number of shadings with this property. Find the remainder when $N$ is divided by $1000$ .

AIME I 2007-10.png

Problem 11

For each positive integer $p$ , let $b(p)$ denote the unique positive integer $k$ such that $|k-sqrt{p}| < frac{1}{2}$ . For example, $b(6) = 2$ and $b(23) = 5$ . If $S = sum_{p=1}^{2007} b(p),$ find the remainder when $S$ is divided by 1000.

Problem 12

In isosceles triangle $ABC$ , $A$ is located at the origin and $B$ is located at (20,0). Point $C$ is in the first quadrant with $AC = BC$ and angle $BAC = 75^{circ}$ . If triangle $ABC$ is rotated counterclockwise about point $A$ until the image of $C$ lies on the positive $y$ -axis, the area of the region common to the original and the rotated triangle is in the form $psqrt{2} + qsqrt{3} + rsqrt{6} + s$ , where $p,q,r,s$ are integers. Find $(p-q+r-s)/2$ .

Problem 13

A square pyramid with base $ABCD$ and vertex $E$ has eight edges of length 4. A plane passes through the midpoints of $AE$ , $BC$ , and $CD$ . The plane's intersection with the pyramid has an area that can be expressed as $sqrt{p}$ . Find $p$ .

AIME I 2007-13.png

Problem 14

A sequence is defined over non-negative integral indexes in the following way: $a_{0}=a_{1}=3$ , $a_{n+1}a_{n-1}=a_{n}^{2}+2007$ .

Find the greatest integer that does not exceed $frac{a_{2006}^{2}+a_{2007}^{2}}{a_{2006}a_{2007}}$

Problem 15

Let $ABC$ be an equilateral triangle, and let $D$ and $F$ be points on sides $BC$ and $AB$ , respectively, with $FA = 5$ and $CD = 2$ . Point $E$ lies on side $CA$ such that angle $DEF = 60^{circ}$ . The area of triangle $DEF$ is $14sqrt{3}$ . The two possible values of the length of side $AB$ are $p pm q sqrt{r}$ , where $p$ and $q$ are rational, and $r$ is an integer not divisible by the square of a prime. Find $r$ .

2007AIME I详细解析

The prime factorization of $24$ is $2^3cdot3$ . Thus, each square must have at least $3$ factors of $2$ and $1$ factor of $3$ and its square root must have $2$ factors of $2$ and $1$ factor of $3$ . This means that each square is in the form $(12c)^2$ , where $12 c$ is a positive integer less than $sqrt{10^6}$ . There are $leftlfloor frac{1000}{12}rightrfloor = boxed{083}$ solutions.
Clearly we have people moving at speeds of $6,8$ and $10$ feet/second. Notice that out of the three people, Cy is at the largest disadvantage to begin with and since all speeds are close, it is hardest for him to catch up. Furthermore, Bob is clearly the farthest along. Thus it is reasonable to assume that there is some point when Al is halfway between Cy and Bob. At this time $s$ , we have that $frac{8(s-4)+10(s-2)}{2}=6s$ After solving, $s=frac{26}{3}$ . At this time, Al has traveled $6cdotfrac{26}{3}=52$ feet.We could easily check that Al is in the middle by trying all three possible cases. $frac{6s + 8(s-4)}{2} = 10(s-2)$ yields that $s = frac 43$ , which can be disregarded since both Bob and Cy hadn't started yet. $frac{6s + 10(s-2)}{2} = 8(s-4)$ yields that $-10=-32$ , a contradiction. Thus, the answer is $boxed{052}$ .
Squaring, we find that $(9 + bi)^2 = 81 + 18bi - b^2$ . Cubing and ignoring the real parts of the result, we find that $(81 + 18bi - b^2)(9 + bi) = ldots + (9cdot 18 + 81)bi - b^3i$ .Setting these two equal, we get that $18bi = 243bi - b^3i$ , so $b(b^2 - 225) = 0$ and $b = -15, 0, 15$ . Since $b > 0$ , the solution is $boxed{015}$ .
Denote the planets $A, B, C$ respectively. Let $a(t), b(t), c(t)$ denote the angle which each of the respective planets makes with its initial position after $t$ years. These are given by $a(t) = frac{t pi}{30}$ , $b(t) = frac{t pi}{42}$ , $c(t) = frac{t pi}{70}$ .In order for the planets and the central star to be collinear, $a(t)$ , $b(t)$ , and $c(t)$ must differ by a multiple of $pi$ . Note that $a(t) - b(t) = frac{t pi}{105}$ and $b(t) - c(t) = frac{t pi}{105}$ , so $a(t) - c(t) = frac{ 2 t pi}{105}$ . These are simultaneously multiples of $pi$ exactly when $t$ is a multiple of $105$ , so the planets and the star will next be collinear in $boxed{105}$ years.This problem is trivialized since the answer is the LCM/GCF of $60,84,140$ . This is just $420/4$ which is $boxed{105}$ -Brudder
Examine modulo 9.
- If $F - 32 equiv 0 pmod{9}$ , then we can define $9x = F - 32$ . This shows that $F = left[frac{9}{5}left[frac{5}{9}(F-32)right] + 32right] Longrightarrow F = left[frac{9}{5}(5x) + 32right] Longrightarrow F = 9x + 32$ . This case works.
- If $F - 32 equiv 1 pmod{9}$ , then we can define $9x + 1 = F - 32$ . This shows that $F = left[frac{9}{5}left[frac{5}{9}(F-32)right] + 32right] Longrightarrow F = left[frac{9}{5}(5x + 1) + 32right] Longrightarrow$ $F = left[9x + frac{9}{5}+ 32 right] Longrightarrow F = 9x + 34$ . So this case doesn't work.
Generalizing this, we define that $9x + k = F - 32$ . Thus, $F = left[frac{9}{5}left[frac{5}{9}(9x + k)right] + 32right] Longrightarrow F = left[frac{9}{5}(5x + left[frac{5}{9}kright]) + 32right] Longrightarrow F = left[frac{9}{5} left[frac{5}{9}k right] right] + 9x + 32$ . We need to find all values $0 le k le 8$ that $left[ frac{9}{5} left[ frac{5}{9} k right] right] = k$ . Testing every value of $k$ shows that $k = 0, 2, 4, 5, 7$ , so $5$ of every $9$ values of $k$ work.

There are $lfloor frac{1000 - 32}{9} rfloor = 107$ cycles of $9$ , giving $5 cdot 107 = 535$ numbers that work. Of the remaining $6$ numbers from $995$ onwards, $995, 997, 999, 1000$ work, giving us $535 + 4 = 539$ as the solution.

Notice that $left[ frac{9}{5} left[ frac{5}{9} k right] right] = k$ holds if $k=left[ frac{9}{5}xright]$ for some $x$ . Thus, after translating from $Fto F-32$ we want count how many values of $x$ there are such that $k=left[ frac{9}{5}xright]$ is an integer from $0$ to $968$ . This value is computed as $left[968*frac{5}{9}right]+1$ , adding in the extra solution corresponding to $0$ .

Let $c$ be a degree Celsius, and $f=frac 95c+32$ rounded to the nearest integer. Since $f$ was rounded to the nearest integer we have $|f-((frac 95)c+32)|leq 1/2$ , which is equivalent to $|(frac 59)(f-32)-c|leq frac 5{18}$ if we multiply by $5/9$ . Therefore, it must round to $c$ because $frac 5{18}<frac 12$ so $c$ is the closest integer. Therefore there is one solution per degree celcius in the range from $0$ to $(frac 59)(1000-32) + 1=(frac 59)(968) + 1=538.8$ , meaning there are $539$ solutions.
Let us keep a careful tree of the possible number of paths around every multiple of .From , we can end at either (mult. of 3) or (mult. of 13).
- Only path leads to
  - Continuing from $12$ , there is $1 cdot 1 = 1$ way to continue to $24$
  - There are $1 cdot left(frac{24-15}{3} + 1right) = 4$ ways to reach $26$ .
- There are ways to reach .
  - Continuing from $13$ , there are $5 cdot 1 = 5$ ways to get to $24$
  - There are $5 cdot left(frac{24-15}{3} + 1 + 1right) = 25$ ways (the first 1 to make it inclusive, the second to also jump from $13 Rightarrow 26$ ) to get to $26$ .
Regrouping, work from $24 | 26Rightarrow 39$
- There are ways to get to
  - Continuing from $24$ , there are $6 cdot left(frac{39 - 27}{3}right) = 24$ ways to continue to $39$ .
- There are ways to reach .
  - Continuing from $26$ , there are $29 cdot left(frac{39-27}{3} + 1right) = 145$ (note that the 1 is not to inclusive, but to count $26 Rightarrow 39$ ).
In total, we get $145 + 24 = 169$ .

In summary, we can draw the following tree, where in $(x,y)$ , $x$ represents the current position on the number line, and $y$ represents the number of paths to get there:
$(12,1)$

$(24,1)$

$(39,4)$

$(26,4)$

$(39,20)$
$(13,5)$

$(24,5)$

$(39,20)$

$(26,25)$

$(39,125)$
Again, this totals $4 + 20 + 20 + 125 = 169$ .

We divide it into 3 stages. The first occurs before the frog moves past 13. The second occurs before it moves past 26, and the last is everything else.

For the first stage the possible paths are $(0,13)$ , $(0,3,13)$ , $(0,3,6,13)$ , $(0,3,6,9,13)$ , $(0,3,6,9,12,13)$ , and $(0,3,6,9,12)$ . That is a total of 6.

For the second stage the possible paths are $(26)$ , $(15,26)$ , $(15,18,26)$ , $(15,18,21,26)$ , $(15,18,21,24,26)$ , and $(15,18,21,24)$ . That is a total of 6.

For the third stage the possible paths are $(39)$ , $(27,39)$ , $(27,30,39)$ , $(27,30,33,39)$ , and $(27,30,33,36,39)$ . That is a total of 5.

However, we cannot jump from $12 Rightarrow 26$ (this eliminates 5 paths) or $24 Rightarrow 39$ (this eliminates 6 paths), so we must subtract $6 + 5 = 11$ .

The answer is $6*6*5 - 11=169$

Another way would be to use a table representing the number of ways to reach a certain number

$begin{tabular}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} 0 & 3 & 6 & 9 & 12 & 13 & 15 & 18 & 21 & 24 & 26 & 27 & 30 & 33 & 36 hline 1 & 1 & 1 & 1 & 1 & 5 & 6 & 6 & 6 & 6 & 29 & 35 & 35 & 35 & 35 end{tabular}$

How we came with each value is to just add in the number of ways that we can reach that number from previous numbers. For example, for $26$ , we can reach it from $13, 15, 18, 21, 24$ , so we add all those values to get the value for $26$ . For $27$ , it is only reachable from $24$ or $26$ , so we have $29 + 6 = 35$ .

The answer for $39$ can be computed in a similar way to get $35 * 4 + 29 = boxed{169}$ .
The ceiling of a number minus the floor of a number is either equal to zero (if the number is an integer); otherwise, it is equal to 1. Thus, we need to find when or not $log_{sqrt{2}} k$ is an integer.The change of base formula shows that $frac{log k}{log sqrt{2}} = frac{2 log k}{log 2}$ . For the $log 2$ term to cancel out, $k$ is a power of $2$ . Thus, $N$ is equal to the sum of all the numbers from 1 to 1000, excluding all powers of 2 from $2^0 = 1$ to $2^9 = 512$ .The formula for the sum of an arithmetic sequence and the sum of a geometric sequence yields that our answer is $left[frac{(1000 + 1)(1000)}{2} - (1 + 2 + 2^2 + ldots + 2^9)right] mod{1000}$ .Simplifying, we get $left[1000left(frac{1000+1}{2}right) -1023right] mod{1000} equiv [500-23] mod{1000} equiv 477 mod{1000}.$ The answer is $boxed{477}$
We can see that $Q_1$ and $Q_2$ must have a root in common for them to both be factors of the same cubic.Let this root be $a$ .We then know that $a$ is a root of $Q_{2}(x)-2Q_{1}(x) = 2x^{2}+2kx-43x+k-2x^{2}-2kx+58x+2k = 15x+3k = 0$ , so $x = frac{-k}{5}$ .We then know that $frac{-k}{5}$ is a root of $Q_{1}$ so we get: $frac{k^{2}}{25}+(k-29)left(frac{-k}{5}right)-k = 0 = k^{2}-5(k-29)(k)-25k = k^{2}-5k^{2}+145k-25k$ or $k^{2}=30k$ , so $k=30$ is the highest.We can trivially check into the original equations to find that $k=30$ produces a root in common, so the answer is $030$ .Again, let the common root be $a$ ; let the other two roots be $m$ and $n$ . We can write that $(x - a)(x - m) = x^2 + (k - 29)x - k$ and that $2(x - a)(x - n) = 2left(x^2 + left(k - frac{43}{2}right)x + frac{k}{2}right)$ .Therefore, we can write four equations (and we have four variables), $a + m = 29 - k$ , $a + n = frac{43}{2} - k$ , $am = -k$ , and $an = frac{k}{2}$ .The first two equations show that $m - n = 29 - frac{43}{2} = frac{15}{2}$ . The last two equations show that $frac{m}{n} = -2$ . Solving these show that $m = 5$ and that $n = -frac{5}{2}$ . Substituting back into the equations, we eventually find that $k = ==30==$
Label the points as in the diagram above. If we draw $overline{O_1A}$ and $overline{O_2B}$ , we form two right triangles. As $overline{AF}$ and $overline{AD}$ are both tangents to the circle, we see that $overline{O_1A}$ is an angle bisector. Thus, $triangle AFO_1 cong triangle ADO_1$ . Call $x = AD = AF$ and $y = EB = BG$ . We know that $x + y + 2r = 34$ .If we call $angle CAB = theta$ , then $angle DAO_1 = frac{180 - theta}{2}$ . Apply the tangent half-angle formula ( $tan frac{theta}{2} = sqrt{frac{1 - cos theta}{1 + cos theta}}$ ). We see that $frac rx = tan frac{180 - theta}{2} = sqrt{frac{1 - cos (180 - theta)}{1 + cos (180 - theta)}}$ $= sqrt{frac{1 + cos theta}{1 - cos theta}}$ . Also, $cos theta = frac{30}{34} = frac{15}{17}$ . Thus, $frac rx = sqrt{frac{1 + frac{15}{17}}{1 - frac{15}{17}}}$ , and $x = frac{r}{4}$ .Similarly, we find that $y = r/sqrt{frac{1 + frac{8}{17}}{1 - frac{8}{17}}} = frac{3r}{5}$ .Therefore, $x + y + 2r = frac{r}{4} + frac{3r}{5} + 2r = frac{57r}{20} = 34 Longrightarrow r = frac{680}{57}$ , and $p + q = 737$ .

Solution 2

Use a similar solution to the aforementioned solution. Instead, call $angle CAB = 2theta$ , and then proceed by simplifying through identities. We see that $frac rx = tan left(frac{180 - 2theta}{2}right) = tan (90 - theta)$ . In terms of $r$ , we find that $x = frac{r}{cot theta} = frac{rsin theta}{cos theta}$ . Similarly, we find that $y = frac{r sin(45 - theta)}{cos (45 - theta)}$ .

Substituting, we find that $rleft(frac{sin theta}{cos theta} + frac{sin(45 - theta)}{cos (45 - theta)} + 2right) = 34$ . Under a common denominator, $rleft(frac{sin theta cos (45 - theta) + cos theta sin (45 - theta)}{cos theta cos (45 - theta)} + 2right) = 34$ . Trigonometric identities simplify this to $rleft(frac{sinleft((theta) + (45 - theta)right)}{frac 12 left(cos (theta + 45 - theta) + cos (theta - 45 + theta) right)} + 2right) = 34$ . From here, it is possible to simplify:

$rleft(frac{2 sin 45}{cos 45 + cos 2theta cos 45 + sin 2theta sin 45} +2right) = 34$

$rleft(frac{2}{frac{17}{17} + frac{8}{17} + frac{15}{17}} + 2right) = 34$

$rleft(frac{57}{20}right) = 34$

Our answer is $34 cdot frac{20}{57} = frac{680}{57}$ , and $p + q = 737$ .

Solution 3

Let the point where CB's extension hits the circle be G, and the point where the hypotenuse hits that circle be E. Clearly $EB=GB$ . Let $EB=x$ . Draw the two perpendicular radii to G and E. Now we have a cyclic quadrilateral. Let the radius be length $r$ . We see that since the cosine of angle ABC is $frac{15}{17}$ the cosine of angle EBG is $-frac{15}{17}$ . Since the measure of the angle opposite to EBG is the complement of this one, its cosine is $frac{15}{17}$ . Using the law of cosines, we see that $x^{2}+x^{2}+frac{30x^{2}}{17}=r^{2}+r^{2}-frac{30r^{2}}{17}$ This tells us that $r=4x$ .

Now look at the other end of the hypotenuse. Call the point where CA hits the circle F and the point where the hypotenuse hits the circle D. Draw the radii to F and D and we have cyclic quadrilaterals once more. Using the law of cosines again, we find that the length of our tangents is $2.4x$ . Note that if we connect the centers of the circles we have a rectangle with sidelengths 8x and 4x. So, $8x+2.4x+x=34$ . Solving we find that $4x=frac{680}{57}$ so our answer is 737.

Solution 4

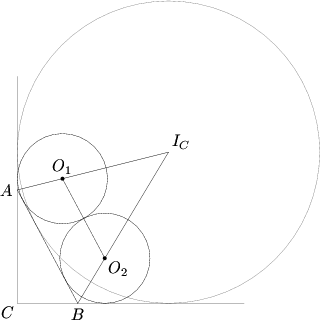
By Pythagoras, $AB = 34$ . Let $I_{C}$ be the $C$ -excenter of triangle $ABC$ . Then the $C$ -exradius $r_{C}$ is given by $r_{C}= frac{K}{s-c}= frac{240}{40-34}= 40$ .

The circle with center $O_{1}$ is tangent to both $AB$ and $AC$ , which means that $O_{1}$ lies on the external angle bisector of $angle BAC$ . Therefore, $O_{1}$ lies on $AI_{C}$ . Similarly, $O_{2}$ lies on $BI_{C}$ .

Let $r$ be the common radius of the circles with centers $O_{1}$ and $O_{2}$ . The distances from points $O_{1}$ and $O_{2}$ to $AB$ are both $r$ , so $O_{1}O_{2}$ is parallel to $AB$ , which means that triangles $I_{C}AB$ and $I_{C}O_{1}O_{2}$ are similar.

The distance from $I_{C}$ to $AB$ is $r_{C}= 40$ , so the distance from $I_{C}$ to $O_{1}O_{2}$ is $40-r$ . Therefore,

$frac{40-r}{40}= frac{O_{1}O_{2}}{AB}= frac{2r}{34}quad Rightarrow quad r = frac{680}{57}$ .

Hence, the final answer is $680+57 = 737$ .

Solution 5

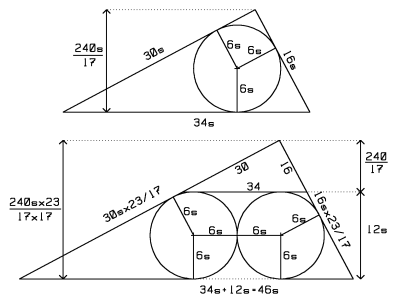
Start with a scaled 16-30-34 triangle. Inscribe a circle. The height, $h,$ and radius, $r,$ are found via $A=frac{1}{2}times 16stimes 30s=frac{1}{2}times 34stimes h=frac{1}{2}times rp,$ where $p$ is the perimeter.

Cut the figure through the circle and perpendicular to the hypotenuse. Slide the two pieces in opposite directions along the hypotenuse until they are one diameter of the circle apart. Complete the two partial circles.

The linear dimensions of the new triangle are $frac{46s}{34s}=frac{23}{17}$ times the size of the original. The problem's 16-30-34 triangle sits above the circles. Equate heights and solve for $r=6s$ :

$frac{240s}{17}timesfrac{23}{17} = frac{240}{17}+12s$

$20stimes 23 = 20times 17+stimes 17times 17$

$s = frac{340}{171}$

$r = 6s = frac{680}{57}$

The answer is $737$ .

Solution 6

Using homothecy in the diagram above, as well as the auxiliary triangle, leads to the solution.

Solution 7

A different approach is to plot the triangle on the Cartesian Plane with $C$ at $(0,0)$ , $A$ at $(0,30)$ , and $B$ at $(16,0)$ . We wish to find the coordinates of $O_1$ and $O_2$ in terms of the radius, which will be expressed as $r$ in the rest of this solution. When we know the coordinates, we will set the distance between the 2 points equal to $2r$ . All points $r$ units away from $overline{AB}$ are on the line with slope $-frac{15}{8}$ , and y-intercept $30+ frac{17}{8} r$

$O_1$ will have x-coordinate $r$ and likewise $O_2$ will have y-coordinate $r$ plugging this into the equation for the line mentioned in the sentence above gives us:

$O_1 = left(r,frac14 r+30right)$ and $O_2 = left(frac35 r+16,rright)$

By the distance formula and the fact that the circles and tangent, we have: $left(16-frac25 rright)^2 + left(30-frac34 rright)^2 = (2r)^2$

which simplifies into the quadratic equation: $1311 r^2 + 23120 r - 462400 = 0$

And by the quadratic equation, the solutions are: $frac{-23120 pm 54400}{2622}$ The solution including the " $-$ " is extraneous so we have the radius equal to $frac{31280}{2622}$

Which simplifies to $frac{680}{57}$ . The sum of the numerator and the denominator is $boxed{737}$

Solution 8 (simple algebra)

It is known that $O_1O_2$ is parallel to AB. Thus, extending $O_1F$ and $GO_2$ to intersect at H yields similar triangles $O_1O_2H$ and BAC, so that $O_1O_2 = 2r$ , $O_1H = frac{16r}{17}$ , and $HO_2 = frac{30r}{17}$ . It should be noted that $O_2G = r$ . Also, FHGC is a rectangle, and so AF = $frac{47r}{17} - 30$ and similarly for BG. Because tangents to a circle are equal, the hypotenuse can be expressed in terms of r: $[2r + frac{47r}{17} - 30 + frac{33r}{17} - 16 = 34]$ Thus, r = $frac{680}{57}$ , and the answer is $boxed{737}.$
Consider the first column. There are ways that the rows could be chosen, but without loss of generality let them be the first three rows. (Change the order of the rows to make this true.) We will multiply whatever answer we get by 20 to get our final answer.Now consider the 3x3 that is next to the 3 boxes we have filled in. We must put one ball in each row (since there must be 2 balls in each row and we've already put one in each). We split into three cases:
- All three balls are in the same column. In this case, there are 3 choices for which column that is. From here, the bottom half of the board is fixed.
- Two balls are in one column, and one is in the other. In this case, there are 3 ways to choose which column gets 2 balls and 2 ways to choose which one gets the other ball. Then, there are 3 ways to choose which row the lone ball is in. Now, what happens in the bottom half of the board? Well, the 3 boxes in the column with no balls in the top half must all be filled in, so there are no choices here. In the column with two balls already, we can choose any of the 3 boxes for the third ball. This forces the location for the last two balls. So we have $3 cdot 2 cdot 3 cdot 3 = 54$ .
- All three balls are in different columns. Then there are 3 ways to choose which row the ball in column 2 goes and 2 ways to choose where the ball in column 3 goes. (The location of the ball in column 4 is forced.) Again, we think about what happens in the bottom half of the board. There are 2 balls in each row and column now, so in the 3x3 where we still have choices, each row and column has one square that is not filled in. But there are 6 ways to do this. So in all there are 36 ways.
So there are $20(3+54+36) = 1860$ different shadings, and the solution is $860$ .

Solution 2

We start by showing that every group of $6$ rows can be grouped into $3$ complementary pairs. We proceed with proof by contradiction. Without loss of generality, assume that the first row has columns $1$ and $2$ shaded. Note how if there is no complement to this, then all the other five rows must have at least one square in the first two columns shaded. That means that in total, the first two rows have $2+5=7$ squares shaded in- that is false since it should only be $6$ . Thus, there exists another row that is complementary to the first. We remove those two and use a similar argument again to show that every group of $6$ rows can be grouped into $3$ complementary pairs.

Now we proceed with three cases.
- There are $frac{binom42}2=3$ pairs of complementary pairs. The first case is that the three pairs are all different, meaning that every single possible pair of shaded squares is used once. This gives us $6!=720.$
- Our second case is that two of the pairs are the same, and the third is different. We have $3$ to choose the pair that shows up twice and $2$ for the other, giving us $3cdot2cdotbinom62binom42binom21=6cdot15cdot6cdot2=1080.$
- Our final case is that all three pairs are the same. This is just $3cdotbinom63=60.$
Our answer is thus $720+1080+60=1860,$ leaving us with a final answer of $boxed{860}.$

Solution 3

We draw a bijection between walking from $(0,0,0,0)$ to $(3,3,3,3)$ as follows: if in the $i$ th row, the $j$ th and $k$ th columns are shaded, then the $(2i-1)$ st step is in the direction corresponding to $j$ , and the $(2i)$ th step is in the direction corresponding to $k$ ( $j < k$ ) here. We can now use the Principle of Inclusion-Exclusion based on the stipulation that $j!=k$ to solve the problem:

$frac{1}{2^6}left(frac{12!}{3!^4}-4cdot{6 choose 1}frac{10!}{3!^3}+4cdot 3cdot{6 choose 2}frac{8!}{3!^2}-4cdot 3cdot 2cdot{6 choose 3}frac{6!}{3!}+4cdot 3cdot 2cdot 1cdot {6 choose 4}4!right) = 1860$

So that the answer is $860$ .

Solution 4

There are ${6choose3}$ to choose the arrangement of the shaded squares in each column. Examine the positioning of the shaded squares in the first two columns:

One example of each case for the first two columns
- If column 1 and column 2 do not share any two filled squares on the same row, then there are ${6choose3}$ combinations for column 1, and then column 2 is fixed. Now, any row cannot have more than 2 shaded squares, so after we pick three more squares in the third column, the fourth column is also fixed. This gives ${6choose3}^2 = 400$ arrangements.
- If column 1 and column 2 share 1 filled square on the same row (6 places), then they each share 1 filled square on a row ( $6 - 1 = 5$ places), share another empty square on a row, and have 2 squares each on different rows. This gives $6 cdot 5 cdot {4choose2} = 180$ . Now, the third and fourths columns must also share a fixed shared shaded square in the row in which the first two columns both had spaces, and another fixed empty square. The remaining shaded squares can only go in 4 places, so we get ${4choose2} = 6$ . We get $180 cdot 6 = 1080$ .
- If column 1 and column 2 share 2 filled squares on the same row ( ${6choose2} = 15$ places), they must also share 2 empty squares on the same row ( ${4choose2} = 6$ ). The last two squares can be arranged in ${2choose1} = 2$ positions; this totals to $15 cdot 6 cdot 2 = 180$ . Now, the third and fourth columns have a fixed 2 filled squares in common rows and 2 empty squares in common rows. The remaining 2 squares have ${2choose1} = 2$ places, giving $180 cdot 2 = 360$ .
- If column 1 and column 2 share 3 filled squares on the same row ( ${6choose3} = 20$ places), then the squares on columns 3 and 4 are fixed.
Thus, there are $400 + 1080 + 360 + 20 = 1860$ number of shadings, and the solution is $860$ .

Solution 5

Consider all possible shadings for a single row. There are ${4 choose 2}=6$ ways to do so, and denote these as $a=1+2$ , $b=3+4$ , $c=1+4$ , $d=2+3$ , $e=1+3$ , and $f=2+4$ where $x+y$ indicates that columns $x$ and $y$ are shaded. From our condition on the columns, we have $a+c+e=a+d+f=b+d+e=b+c+f=3$ Summing the first two and the last two equations, we have $2a+c+d+e+f=6=2b+c+d+e+f$ , from which we have $a=b$ . Likewise, $c=d$ and $e=f$ since these pairs shade in complimentary columns. So the six rows are paired up into a row and its compliment. In all, we can have 3 a's and 3 b's and similar setups for $c$ / $d$ and $e$ / $f$ , 2 a's, 2 b's, 1 c and 1 d and similar setups for all six arrangements, or one of each. This first case gives $3{6 choose 3}=60$ solutions; the second gives $6cdot 6cdot5cdot{4 choose 2}=1080$ solutions, and the final case gives $6!=720$ solutions. In all, we have 1860 solutions, for an answer of $860$ .

Solution 6

Each shading can be brought, via row swapping operations, to a state with a $3times2$ shaded $L$ in the lower left hand corner. The number of such arrangements multiplied by ${5 choose 2}{3choose 2}$ will be the total. Consider rows 2 and 3 up from the bottom: they each have one of their allotted two squares shaded. Depending how the remaining three shades are distributed, the column totals of columns 2,3, and 4 from the left can be of the form ${3,0,0},{0,1,2},{1,1,1}$ . Form 1: The entire lower left $3times2$ rectangle is shaded, forcing the opposite $3times2$ rectangle to also be shaded; thus 1 arrangement Form 2: There is a column with nothing shaded in the bottom right $3times2$ , so it must be completely shaded in the upper right $3times2$ . Now consider the upper right half column that will have $1$ shade. There are $3$ ways of choosing this shade, and all else is determined from here; thus 3 arrangements Form 3: The upper right $3times3$ will have exactly $2$ shades per column and row. This is equivalent to the number of terms in a $3times3$ determinant, or $6$ arrangements

Of the $3^2$ ways of choosing to complete the bottom half of the $4times6$ , form 1 is achieved in exactly 1 way; form 2 is achieved in $3times2$ ways; and form $3$ in the remaining $2$ ways. Thus, the weighted total is $1+6times3+2times6=31$ . Complete: $31times60=860mod{1000}$

Solution 7

Note that if we find a valid shading of the first 3 columns, the shading of the last column is determined. We also note that within the first 3 columns, there will be 3 rows with 1 shaded square and 3 rows with 2 shaded squares.

There are ${6 choose 3}$ ways to choose which rows have 1 shaded square (which we'll call a "1-row") within the first 3 columns and which rows have 2 (we'll call these "2-rows") within the first 3 columns. Next, we do some casework:
- If all of the shaded squares in the first column are in a 1-row, then the squares in the second and third columns must be in the 2-rows. Thus there is only ${3 choose 3}{3 choose 0} times 1= 1$ valid shading in this case.
- If 2 of the shaded squares in the first column are in a 1-row, and the third shaded square is in a 2-row, then the other shaded square in that 2-row can either be in column 3 or column 4. Once we determine that, the other shaded squares are uniquely determined. Thus, there are ${3 choose 2}{3 choose 1}times 2=18$ valid shadings in this case.
- If 1 shaded square in the first column is in a 1-row, and the other 2 are in 2-rows, then the 2-row without a shaded square in the first column must have shaded squares in both column 2 and column 3. This leaves 4 possible squares in the second column to be shaded (since there can't be another shaded square in the occupied 1-row). Thus, there are ${3 choose 1}{3 choose 2}times {4 choose 2}=54$ valid shadings in this case. (We only need to choose 2, since 1 of the shaded squares in the third column must go to the unoccupied 2-row).
- If all of the shaded squares in the first column are in the 3 2-rows, then if we choose any 3 squares in the second column to be shaded, then the third column is uniquely determined to create a valid shading. Thus, there are ${3 choose 0}{3 choose 3}times{6 choose 3} = 20$ valid shadings in this case.
In total, we have ${6choose3}(1+18+54+20)=20*93=1860$ . Thus our answer is $boxed{860}$ .

Solution 8

We can use generating functions. Suppose that the variables $a$ , $b$ , $c$ , and $d$ represent shading a square that appears in the first, second, third, or fourth columns, respectively. Then if two squares in the row are shaded, then the row is represented by the generating function $ab+ac+ad+bc+bd+cd$ , which we can write as $P(a,b,c,d)=(ab+cd)+(a+b)(c+d)$ . Therefore, $P(a,b,c,d)^6$ represents all of the possible ways to color six rows such that each row has two shaded squares. We only want the possibilities when each column has three shaded squares, or rather, the coefficient of $a^3b^3c^3d^3$ in $P(a,b,c,d)^6$ .

By the Binomial Theorem, $[P(a,b,c,d)^6=sum_{k=0}^6 binom{6}{k} (ab+cd)^k(a+b)^{6-k}(c+d)^{6-k}.tag{1}]$ If we expand $(ab+cd)^k$ , then the powers of $a$ and $b$ are always equal. Therefore, to obtain terms of the form $a^3b^3c^3d^3$ , the powers of $a$ and $b$ in $(a+b)^{6-k}$ must be equal. In particular, only the central term in the binomial expansion will contribute, and this implies that $k$ must be even. We can use the same logic for $c$ and $d$ . Therefore, the coefficient of $a^3b^3c^3d^3$ in the following expression is the same as the coefficient of $a^3b^3c^3d^3$ in (1). $[sum_{k=0}^3 binom{6}{2k} (ab+cd)^{2k}(ab)^{3-k}(cd)^{3-k}binom{6-2k}{3-k}^2.tag{2}]$ Now we notice that the only way to obtain terms of the form $a^3b^3c^3d^3$ is if we take the central term in the binomial expansion of $(ab+cd)^{2k}$ . Therefore, the terms that contribute to the coefficient of $a^3b^3c^3d^3$ in (2) are $[sum_{k=0}^3 binom{6}{2k}binom{2k}{k}binom{6-2k}{3-k}^2(abcd)^3.]$ This sum is $400+1080+360+20=1860$ so the answer is $boxed{860}$ .
$left(k- frac 12right)^2=k^2-k+frac 14$ and $left(k+ frac 12right)^2=k^2+k+ frac 14$ . Therefore $b(p)=k$ if and only if $p$ is in this range, or $k^2-k<pleq k^2+k$ . There are $2k$ numbers in this range, so the sum of $b(p)$ over this range is $(2k)k=2k^2$ . $44<sqrt{2007}<45$ , so all numbers $1$ to $44$ have their full range. Summing this up with the formula for the sum of the first $n$ squares ( $frac{n(n+1)(2n+1)}{6}$ ), we get $sum_{k=1}^{44}2k^2=2frac{44(44+1)(2*44+1)}{6}=58740$ . We need only consider the $740$ because we are working with modulo $1000$ .Now consider the range of numbers such that $b(p)=45$ . These numbers are $leftlceilfrac{44^2 + 45^2}{2}rightrceil = 1981$ to $2007$ . There are $2007 - 1981 + 1 = 27$ (1 to be inclusive) of them. $27*45=1215$ , and $215+740= boxed{955}$ , the answer.
Solution 1

Let the new triangle be $triangle AB'C'$ ( $A$ , the origin, is a vertex of both triangles). Let $overline{B'C'}$ intersect with $overline{AC}$ at point $D$ , $overline{BC}$ intersect with $overline{B'C'}$ at $E$ , and $overline{BC}$ intersect with $overline{AB'}$ at $F$ . The region common to both triangles is the quadrilateral $ADEF$ . Notice that $[ADEF] = [triangle ADB'] - [triangle EFB']$ , where we let $[ldots]$ denote area.

To find $[triangle ADB']$ :Since and both have measures , both of their complements are , and . We know that , so .

Thus $triangle ADB'$ is a $45 - 60 - 75 triangle$ . It can be solved by drawing an altitude splitting the $75^{circ}$ angle into $30^{circ}$ and $45^{circ}$ angles, forming a $30-60-90$ right triangle and a $45-45-90$ isosceles right triangle. Since we know that $AB' = 20$ , the base of the $30-60-90$ triangle is $10$ , the base of the $45-45-90$ is $10sqrt{3}$ , and their common height is $10sqrt{3}$ . Thus, the total area of $[triangle ADB'] = frac{1}{2}(10sqrt{3})(10sqrt{3} + 10) = boxed{150 + 50sqrt{3}}$ .

To find $[triangle EFB']$ :Since is also a triangle,

$AF = 20sin 75 = 20 sin (30 + 45) = 20left(frac{sqrt{2} + sqrt{6}}4right) = 5sqrt{2} + 5sqrt{6}$ and

$FB' = AB' - AF = 20 - 5sqrt{2} - 5sqrt{6}$ Since . With some horrendous algebra, we can calculate

To finish, $begin{align*} [ADEF] &= [triangle ADB'] - [triangle EFB'] &= left(150 + 50sqrt{3}right) - left(-500sqrt{2} + 400sqrt{3} - 300sqrt{6} + 750right) &=500sqrt{2} - 350sqrt{3} + 300sqrt{6} - 600 end{align*}$ Hence, $frac{p-q+r-s}{2} = frac{500 + 350 + 300 + 600}2 = frac{1750}2 = boxed{boxed{875}}$ .

Solution 2

Redefine the points in the same manner as the last time ( $triangle AB'C'$ , intersect at $D$ , $E$ , and $F$ ). This time, notice that $[ADEF] = [triangle AB'C'] - ([triangle ADC'] + [triangle EFB']$ .

The area of $[triangle AB'C'] = [triangle ABC]$ . The altitude of $triangle ABC$ is clearly $10 tan 75 = 10 tan (30 + 45)$ . The tangent addition rule yields $10(2 + sqrt{3})$ (see above). Thus, $[triangle ABC] = frac{1}{2} 20 cdot (20 + 10sqrt{3}) = 200 + 100sqrt{3}$ .

The area of $[triangle ADC']$ (with a side on the y-axis) can be found by splitting it into two triangles, $30-60-90$ and $15-75-90$ right triangles. $AC' = AC = frac{10}{sin 15}$ . The sine subtraction rule shows that $frac{10}{sin 15} = frac{10}{frac{sqrt{6} - sqrt{2}}4} = frac{40}{sqrt{6} - sqrt{2}} = 10(sqrt{6} + sqrt{2})$ . $AC'$ , in terms of the height of $triangle ADC'$ , is equal to $h(sqrt{3} + tan 75) = h(sqrt{3} + 2 + sqrt{3})$ . $begin{align*} [ADC'] &= frac 12 AC' cdot h &= frac 12 (10sqrt{6} + 10sqrt{2})left(frac{10sqrt{6} + 10sqrt{2}}{2sqrt{3} + 2}right) &= frac{(800 + 400sqrt{3})}{(2 + sqrt{3})}cdotfrac{2 - sqrt{3}}{2-sqrt{3}} &= frac{400sqrt{3} + 400}8 = 50sqrt{3} + 50 end{align*}$

The area of $[triangle EFB']$ was found in the previous solution to be $- 500sqrt{2} + 400sqrt{3} - 300sqrt{6} +750$ .

Therefore, $[ADEF]$ $= (200 + 100sqrt{3}) - left((50 + 50sqrt{3}) + (-500sqrt{2} + 400sqrt{3} - 300sqrt{6} +750)right)$ $= 500sqrt{2} - 350sqrt{3} + 300sqrt{6} - 600$ , and our answer is $boxed{875}$ .

Solution 3

Call the points of the intersections of the triangles $D$ , $E$ , and $F$ as noted in the diagram (the points are different from those in the diagram for solution 1). $overline{AD}$ bisects $angle EDE'$ .

Through HL congruency, we can find that $triangle AED$ is congruent to $triangle AE'D$ . This divides the region $AEDF$ (which we are trying to solve for) into two congruent triangles and an isosceles right triangle.

$AE = 20 cos 15 = 20 cos (45 - 30) = 20 cdot frac{sqrt{6} + sqrt{2}}{4} = 5sqrt{6} + 5sqrt{2}$ Since , we find that .

Now, we need to find $[AED] = [AE'D]$ . The acute angles of the triangles are $frac{15}{2}$ and $90 - frac{15}{2}$ . By repeated application of the half-angle formula, we can find that $tan frac{15}{2} = sqrt{2} - sqrt{3} + sqrt{6} - 2$ .

The area of $[AED] = frac 12 left(20 cos 15right)^2 left(tan frac{15}{2}right)$ . Thus, $[AED] + [AE'D] = 2left(frac 12((5sqrt{6} + 5sqrt{2})^2 cdot (sqrt{2} - sqrt{3} + sqrt{6} - 2))right)$ , which eventually simplifies to $500sqrt{2} - 350sqrt{3} + 300sqrt{6} - 600$ .

Adding them together, we find that the solution is $[AEDF] = [AE'F] + [AED] + [AE'D]$ $= 100 + 50sqrt{3} + 500sqrt{2} - 350sqrt{3} + 300sqrt{6} - 600=$ $= 500sqrt{2} - 350sqrt{3} + 300sqrt{6} - 600$ , and the answer is $boxed{875}$ .

Solution 4

From the given information, calculate the coordinates of all the points (by finding the equations of the lines, equating). Then, use the shoelace method to calculate the area of the intersection.
- $overline{AC}$ : $y = (tan 75) x = (2 + sqrt{3})x$
- $overline{AB'}$ : $y = (tan 15) x = (2 - sqrt{3})x$
- $overline{BC}$ : It passes thru $(20,0)$ , and has a slope of $-tan75 = -(2 + sqrt{3})$ . The equation of its line is $y = (2+sqrt{3})(20 - x)$ .
- $overline{B'C'}$ : $AC' = AC = frac{10}{cos 75} = 10sqrt{6} + 10sqrt{2}$ , so it passes thru point $(0, 10sqrt{6} + 10sqrt{2})$ . It has a slope of $-tan 60 = -sqrt{3}$ . So the equation of its line is $y = -sqrt{3}x + 10(sqrt{6} + sqrt{2})$ .
Now, we can equate the equations to find the intersections of all the points.
- $A (0,0)$
- $D$ is the intersection of $overline{BC}, overline{B'C'}$ . $(2+sqrt{3})(20-x) = -sqrt{3}x + 10(sqrt{6} + sqrt{2})$ . Therefore, $x = 5(4 + 2sqrt{3}-sqrt{6}-sqrt{2})$ , $y = 5(3sqrt{6} + 5sqrt{2}-4sqrt{3}-6)$ .
- $E$ is the intersection of $overline{AB'}, overline{BC}$ . $(2 - sqrt{3})x =(2+sqrt{3})(20-x)$ . Therefore, $x = 5(2+sqrt{3})$ , $y = 5$ .
- $F$ is the intersection of $overline{AC}, overline{B'C'}$ . $(2+sqrt{3})x = -sqrt{3}x + 10(sqrt{6} + sqrt{2})$ . Therefore, $x = 5sqrt{2}$ , $y = 10sqrt{2}+ 5sqrt{6}$ .
We take these points and tie them together by shoelace, and the answer should come out to be $boxed{875}$ .
Solution 1

Note first that the intersection is a pentagon.

Use 3D analytical geometry, setting the origin as the center of the square base and the pyramid’s points oriented as shown above. $A(-2,2,0), B(2,2,0), C(2,-2,0), D(-2,-2,0), E(0,0,2sqrt{2})$ . Using the coordinates of the three points of intersection $(-1,1,sqrt{2}), (2,0,0), (0,-2,0)$ , it is possible to determine the equation of the plane. The equation of a plane resembles $ax + by + cz = d$ , and using the points we find that $2a = d Longrightarrow d = frac{a}{2}$ , $-2b = d Longrightarrow d = frac{-b}{2}$ , and $-a + b + sqrt{2}c = d Longrightarrow -frac{d}{2} - frac{d}{2} + sqrt{2}c = d Longrightarrow c = dsqrt{2}$ . It is then $x - y + 2sqrt{2}z = 2$ .

$[asy]import three; pointpen = black; pathpen = black+linewidth(0.7); currentprojection = perspective(2.5,-12,4); triple A=(-2,2,0), B=(2,2,0), C=(2,-2,0), D=(-2,-2,0), E=(0,0,2*2^.5), P=(A+E)/2, Q=(B+C)/2, R=(C+D)/2, Y=(-3/2,-3/2,2^.5/2),X=(3/2,3/2,2^.5/2); draw(A--B--C--D--A--E--B--E--C--E--D); label("A",A, SE); label("B",B,(1,0,0)); label("C",C, SE); label("D",D, W); label("E",E,N); label("P",P, NW); label("Q",Q,(1,0,0)); label("R",R, S); label("Y",Y,NW); label("X",X,NE); draw(P--X--Q--R--Y--cycle,linetype("6 6")+linewidth(0.7)); [/asy]$ $[asy] pointpen = black; pathpen = black+linewidth(0.7); pair P = (0, 2.5^.5), X = (3/2^.5,0), Y = (-3/2^.5,0), Q = (2^.5,-2.5^.5), R = (-2^.5,-2.5^.5); D(MP("P",P,N)--MP("X",X,NE)--MP("Q",Q)--MP("R",R)--MP("Y",Y,NW)--cycle); D(X--Y,linetype("6 6") + linewidth(0.7)+blue); D(P--(0,-P.y),linetype("6 6") + linewidth(0.7) + red); MP("color{blue}{3sqrt{2}}",(X+Y)/2); MP("2sqrt{2}",(Q+R)/2); MP("color{red}{sqrt{frac{5}{2}}}",(0,-P.y/2),E); MP("color{red}{sqrt{frac{5}{2}}}",(0,2*P.y/5),E); [/asy]$ Write the equation of the lines and substitute to find that the other two points of intersection on $overline{BE}$ , $overline{DE}$ are $left(frac{pm 3}{2},frac{pm 3}{2},frac{sqrt{2}}{2}right)$ . To find the area of the pentagon, break it up into pieces (an isosceles triangle on the top, an isosceles trapezoid on the bottom). Using the distance formula ( $sqrt{a^2 + b^2 + c^2}$ ), it is possible to find that the area of the triangle is $frac{1}{2}bh Longrightarrow frac{1}{2} 3sqrt{2} cdot sqrt{frac 52} = frac{3sqrt{5}}{2}$ . The trapezoid has area $frac{1}{2}h(b_1 + b_2) Longrightarrow frac 12sqrt{frac 52}left(2sqrt{2} + 3sqrt{2}right) = frac{5sqrt{5}}{2}$ . In total, the area is $4sqrt{5} = sqrt{80}$ , and the solution is $boxed{080}$ .

Solution 2

Use the same coordinate system as above, and let the plane determined by $triangle PQR$ intersect $overline{BE}$ at $X$ and $overline{DE}$ at $Y$ . Then the line $overline{XY}$ is the intersection of the planes determined by $triangle PQR$ and $triangle BDE$ .

Note that the plane determined by $triangle BDE$ has the equation $x=y$ , and $overline{PQ}$ can be described by $x=2(1-t)-t, y=t, z=tsqrt{2}$ . It intersects the plane when $2(1-t)-t=t$ , or $t=frac{1}{2}$ . This intersection point has $z=frac{sqrt{2}}{2}$ . Similarly, the intersection between $overline{PR}$ and $triangle BDE$ has $z=frac{sqrt{2}}{2}$ . So $overline{XY}$ lies on the plane $z=frac{sqrt{2}}{2}$ , from which we obtain $X=left( frac{3}{2},frac{3}{2},frac{sqrt{2}}{2}right)$ and $Y=left( -frac{3}{2},-frac{3}{2},frac{sqrt{2}}{2}right)$ . The area of the pentagon $EXQRY$ can be computed in the same way as above.
Solution 1

We are given that

$a_{n+1}a_{n-1}= a_{n}^{2}+2007$ , $a_{n-1}^{2}+2007 = a_{n}a_{n-2}$ .

Add these two equations to get

$a_{n-1}(a_{n-1}+a_{n+1}) = a_{n}(a_{n}+a_{n-2})$

$frac{a_{n+1}+a_{n-1}}{a_{n}}= frac{a_{n}+a_{n-2}}{a_{n-1}}$ .

This is an invariant. Defining $b_{i}= frac{a_{i}}{a_{i-1}}$ for each $i ge 2$ , the above equation means

$b_{n+1}+frac{1}{b_{n}}= b_{n}+frac{1}{b_{n-1}}$ .

We can thus calculate that $b_{2007}+frac{1}{b_{2006}}= b_{3}+frac{1}{b_{2}}= 225$ . Using the equation $a_{2007}a_{2005}=a_{2006}^{2}+2007$ and dividing both sides by $a_{2006}a_{2005}$ , notice that $b_{2007}= frac{a_{2007}}{a_{2006}}= frac{a_{2006}^{2}+2007}{a_{2006}a_{2005}}> frac{a_{2006}}{a_{2005}}= b_{2006}$ . This means that

$b_{2007}+frac{1}{b_{2007}}< b_{2007}+frac{1}{b_{2006}}= 225$ . It is only a tiny bit less because all the $b_i$ are greater than $1$ , so we conclude that the floor of $frac{a_{2007}^{2}+a_{2006}^{2}}{a_{2007}a_{2006}}= b_{2007}+frac{1}{b_{2007}}$ is $224$ .

Solution 2

The equation $a_{n+1}a_{n-1}-a_n^2=2007$ looks like the determinant $[left|begin{array}{cc}a_{n+1}&a_na_n&a_{n-1}end{array}right|=2007.]$ Therefore, the determinant of this matrix is invariant. Guessing that this sequence might be a linear recursion because of the matrix form given below, we define the sequence $b_n$ defined by $b_1=b_2=3$ and $b_{n+1}=alpha b_n+beta b_{n-1}$ for $nge 2$ . We wish to find $alpha$ and $beta$ such that $a_n=b_n$ for all $nge 1$ . To do this, we use the following matrix form of a linear recurrence relation

$[left(begin{array}{cc}b_{n+1}&b_nb_n&b_{n-1}end{array}right)=left(begin{array}{cc}alpha&beta1&0end{array}right)left(begin{array}{cc}b_{n}&b_{n-1}b_{n-1}&b_{n-2}end{array}right).]$

When we take determinants, this equation becomes

$[text{det}left(begin{array}{cc}b_{n+1}&b_nb_n&b_{n-1}end{array}right)=text{det}left(begin{array}{cc}alpha&beta1&0end{array}right)text{det}left(begin{array}{cc}b_{n}&b_{n-1}b_{n-1}&b_{n-2}end{array}right).]$

We want $[text{det}left(begin{array}{cc}b_{n+1}&b_nb_n&b_{n-1}end{array}right)=2007]$ for all $n$ . Therefore, we replace the two matrices by $2007$ to find that

$[2007=text{det}left(begin{array}{cc}alpha&beta1&0end{array}right)cdot 2007]$ $[1=text{det}left(begin{array}{cc}alpha&beta1&0end{array}right)=-beta.]$ Therefore, $beta=-1$ . Computing that $a_3=672$ , and using the fact that $b_3=alpha b_2-b_1$ , we conclude that $alpha=225$ . Clearly, $a_1=b_1$ , $a_2=b_2$ , and $a_3=b_3$ . We claim that $a_n=b_n$ for all $nge 1$ . We proceed by induction. If $a_k=b_k$ for all $kle n$ , then clearly, $[b_nb_{n-2}-b_{n-1}^2=a_na_{n-2}-a_{n-1}^2=2007.]$ We also know by the definition of $b_{n+1}$ that

$[text{det}left(begin{array}{cc}b_{n+1}&b_nb_n&b_{n-1}end{array}right)=text{det}left(begin{array}{cc}alpha&beta1&0end{array}right)text{det}left(begin{array}{cc}b_{n}&b_{n-1}b_{n-1}&b_{n-2}end{array}right).]$

We know that the RHS is $2007$ by previous work. Therefore, $b_{n+1}b_{n-1}-b_n^2=2007$ . After substuting in the values we know, this becomes $b_{n+1}a_{n-1}-a_n^2=2007$ . Thinking of this as a linear equation in the variable $b_{n+1}$ , we already know that this has the solution $b_{n+1}=a_{n+1}$ . Therefore, by induction, $a_n=b_n$ for all $nge 1$ . We conclude that $a_n$ satisfies the linear recurrence $a_{n+1}=225a_n-a_{n-1}$ .

It's easy to prove that $a_n$ is a strictly increasing sequence of integers for $nge 3$ . Now

$[frac{a_{2007}^2+a_{2006}^2}{a_{2007}a_{2006}}=frac{a_{2007}}{a_{2006}}+frac{a_{2006}}{a_{2007}}=frac{225a_{2006}-a_{2005}}{a_{2006}}+frac{a_{2006}}{a_{2007}}.]$

$[=225+frac{a_{2006}}{a_{2007}}-frac{a_{2005}}{a_{2006}}=225+frac{a_{2006}^2-a_{2005}a_{2007}}{a_{2005}a_{2006}}.]$

$[=225-frac{2007}{a_{2005}a_{2006}}.]$

The sequence certainly grows fast enough such that $frac{2007}{a_{2005}a_{2006}}<1$ . Therefore, the largest integer less than or equal to this value is $224$ .

Solution 3 ( generalized )

This is a more elementary and rigorous solution to a slightly generalized version. The defining recursive sequence is generalized to

$[a_{n+1}a_{n-1} = a_n^2 + 9k, ---------(1)]$ where $k$ is a positive integer and $a_0 = a_1 = 3.$

Lemma 1 : For $n geq 1$ , $[a_{n+1} = ( k + 2)a_n - a_{n-1}. ---------(2)]$ We shall prove by induction. From (1), $a_2 = 3k + 3$ . From the lemma, $a_2 = (k + 2) 3 - 3 = 3k + 3.$ Base case proven. Assume that the lemma is true for some $t geq 1$ . Then, eliminating the $a_{t-1}$ using (1) and (2) gives

$[(k+2)a_ta_{t+1} = a_t^2 + a_{t+1}^2 + 9k. ---------(3)]$

It follows from (2) that

$[(k+2)a_{t+1} - a_t =frac{(k+2)a_{t+1}a_t - a_t^2}{a_t} =frac{a_{t+1}^2 + 9k}{a_t} =a_{t+2},]$

where the last line followed from (1) for case $n = t+1$ .

Lemma 2 : For $n geq 0,$ $[a_{n+1} geq a_{n}.]$ Base case is obvious. Assume that $a_{t+1} geq a_{t}$ for some $t geq 0$ . Then it follows that $[a_{t+2} =frac{a_{t+1}^2 + 9k}{a_t} = a_{t+1}(frac{a_{t+1}}{a_t} ) + 9k geq a_{t+1} + 9k > a_{t+1}.]$

This completes the induction.

Lemma 3 : For $n geq 1,$ $[a_n a_{n+1} > 9k]$

Using (1) and Lemma 2, for $n geq 1,$ $[a_{n+1}a_n geq a_{n+1}a_{n-1} = a_n^2 + 9k > 9k]$

Finally, using (3), for $n geq 1,$ $[frac{a_n^2 + a_{n+1}^2}{a_n a_{n+1}} =frac{(k+2)a_n a_{n+1} - 9k}{a_n a_{n+1}} = k+2 -frac{9k}{a_n a_{n+1}}.]$ Using lemma 3, the largest integer less than or equal to this value would be $k + 1$ .

Solution 4 (pure algebra)

We will try to manipulate $frac{a_0^2+a_1^2}{a_0a_1}$ to get $frac{a_1^2+a_2^2}{a_1a_2}$ .

$frac{a_0^2+a_1^2}{a_0a_1} = frac{a_0+frac{a_1^2}{a_0}}{a_1} = frac{a_0+frac{a_1^2+2007}{a_0}-frac{2007}{a_0}}{a_1}$ Using the recurrence relation, $= frac{a_0+a_2-frac{2007}{a_0}}{a_1} = frac{a_0a_2+a_2^2-frac{2007a_2}{a_0}}{a_1a_2}$ Applying the relation to $a_0a_2$ , $= frac{a_1^2+2007+a_2^2-frac{2007a_2}{a_0}}{a_1a_2} = frac{a_1^2+a_2^2}{a_1a_2}+frac{2007}{a_1a_2}-frac{2007}{a_0a_1}$

We can keep on using this method to get that $frac{a_0^2+a_1^2}{a_0a_1} = frac{a_{2006}^2+a_{2007}^2}{a_{2006}a_{2007}}+frac{2007}{a_{2006}a_{2007}}-frac{2007}{a_{2005}a_{2006}}+frac{2007}{a_{2005}a_{2006}}-ldots-frac{2007}{a_{0}a_{1}}$

This telescopes to $frac{a_0^2+a_1^2}{a_0a_1} = frac{a_{2006}^2+a_{2007}^2}{a_{2006}a_{2007}}+frac{2007}{a_{2006}a_{2007}}-frac{2007}{a_{0}a_{1}}$

or $frac{a_{2006}^2+a_{2007}^2}{a_{2006}a_{2007}} = frac{a_0^2+a_1^2}{a_0a_1}+frac{2007}{a_{0}a_{1}}-frac{2007}{a_{2006}a_{2007}}$

Finding the first few values, we notice that they increase rapidly, so $frac{2007}{a_{2006}a_{2007}} < 1$ . Calculating the other values, $frac{a_{2006}^2+a_{2007}^2}{a_{2006}a_{2007}} = 2+223-frac{2007}{a_{2006}a_{2007}}$ .

The greatest number that does not exceed this is $224$
Denote the length of a side of the triangle $x$ , and of $overline{AE}$ as $y$ . The area of the entire equilateral triangle is $frac{x^2sqrt{3}}{4}$ . Add up the areas of the triangles using the $frac{1}{2}absin C$ formula (notice that for the three outside triangles, $sin 60 = frac{sqrt{3}}{2}$ ): $frac{x^2sqrt{3}}{4} = frac{sqrt{3}}{4}(5 cdot y + (x - 2)(x - 5) + 2(x - y)) + 14sqrt{3}$ . This simplifies to $frac{x^2sqrt{3}}{4} = frac{sqrt{3}}{4}(5y + x^2 - 7x + 10 + 2x - 2y + 56)$ . Some terms will cancel out, leaving $y = frac{5}{3}x - 22$ . $angle FEC$ is an external angle to $triangle AEF$ , from which we find that $60 + angle CED = 60 + angle AFE$ , so $angle CED = angle AFE$ . Similarly, we find that $angle EDC = angle AEF$ . Thus, $triangle AEF sim triangle CDE$ . Setting up a ratio of sides, we get that $frac{5}{x-y} = frac{y}{2}$ . Using the previous relationship between $x$ and $y$ , we can solve for $x$ .

$xy - y^2 = 10$

$frac{5}{3}x^2 - 22x - left(frac{5}{3}x - 22right)^2 - 10 = 0$

$frac{5}{3}x^2 - frac{25}{9}x^2 - 22x + 2 cdot frac{5 cdot 22}{3}x - 22^2 - 10= 0$

$10x^2 - 462x + 66^2 + 90 = 0$

Use the quadratic formula, though we only need the root of the discriminant. This is $sqrt{(7 cdot 66)^2 - 4 cdot 10 cdot (66^2 + 90)} = sqrt{49 cdot 66^2 - 40 cdot 66^2 - 4 cdot 9 cdot 100}$ $= sqrt{9 cdot 4 cdot 33^2 - 9 cdot 4 cdot 100} = 6sqrt{33^2 - 100}$ . The answer is $boxed{989}$ .