Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2008AIME II真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月9日下午4:01

2008AIME II真题及答案解析

Problem 1

Of the students attending a school party, $60%$ of the students are girls, and $40%$ of the students like to dance. After these students are joined by $20$ more boy students, all of whom like to dance, the party is now $58%$ girls. How many students now at the party like to dance?

Problem 2

Square $AIME$ has sides of length $10$ units. Isosceles triangle $GEM$ has base $EM$ , and the area common to triangle $GEM$ and square $AIME$ is $80$ square units. Find the length of the altitude to $EM$ in $triangle GEM$ .

Problem 3

Ed and Sue bike at equal and constant rates. Similarly, they jog at equal and constant rates, and they swim at equal and constant rates. Ed covers $74$ kilometers after biking for $2$ hours, jogging for $3$ hours, and swimming for $4$ hours, while Sue covers $91$ kilometers after jogging for $2$ hours, swimming for $3$ hours, and biking for $4$ hours. Their biking, jogging, and swimming rates are all whole numbers of kilometers per hour. Find the sum of the squares of Ed's biking, jogging, and swimming rates.

Problem 4

There exist unique positive integers $x$ and $y$ that satisfy the equation $x^2 + 84x + 2008 = y^2$ . Find $x + y$ .

Problem 5

A right circular cone has base radius $r$ and height $h$ . The cone lies on its side on a flat table. As the cone rolls on the surface of the table without slipping, the point where the cone's base meets the table traces a circular arc centered at the point where the vertex touches the table. The cone first returns to its original position on the table after making $17$ complete rotations. The value of $h/r$ can be written in the form $msqrt {n}$ , where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. Find $m + n$ .

Problem 6

A triangular array of numbers has a first row consisting of the odd integers $1,3,5,ldots,99$ in increasing order. Each row below the first has one fewer entry than the row above it, and the bottom row has a single entry. Each entry in any row after the top row equals the sum of the two entries diagonally above it in the row immediately above it. How many entries in the array are multiples of $67$ ?

Problem 7

Let $S_i$ be the set of all integers $n$ such that $100ileq n < 100(i + 1)$ . For example, $S_4$ is the set ${400,401,402,ldots,499}$ . How many of the sets $S_0, S_1, S_2, ldots, S_{999}$ do not contain a perfect square?

Problem 8

Find the positive integer $n$ such that

$[arctanfrac {1}{3} + arctanfrac {1}{4} + arctanfrac {1}{5} + arctanfrac {1}{n} = frac {pi}{4}.]$

Problem 9

Ten identical crates each of dimensions $3$ ft $times$ $4$ ft $times$ $6$ ft. The first crate is placed flat on the floor. Each of the remaining nine crates is placed, in turn, flat on top of the previous crate, and the orientation of each crate is chosen at random. Let $frac {m}{n}$ be the probability that the stack of crates is exactly $41$ ft tall, where $m$ and $n$ are relatively prime positive integers. Find $m$ .

Problem 10

Let $ABCD$ be an isosceles trapezoid with $overline{AD}||overline{BC}$ whose angle at the longer base $overline{AD}$ is $dfrac{pi}{3}$ . The diagonals have length $10sqrt {21}$ , and point $E$ is at distances $10sqrt {7}$ and $30sqrt {7}$ from vertices $A$ and $D$ , respectively. Let $F$ be the foot of the altitude from $C$ to $overline{AD}$ . The distance $EF$ can be expressed in the form $msqrt {n}$ , where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. Find $m + n$ .

Problem 11

Consider sequences that consist entirely of $A$ 's and $B$ 's and that have the property that every run of consecutive $A$ 's has even length, and every run of consecutive $B$ 's has odd length. Examples of such sequences are $AA$ , $B$ , and $AABAA$ , while $BBAB$ is not such a sequence. How many such sequences have length 14?

Problem 12

On a long straight stretch of one-way single-lane highway, cars all travel at the same speed and all obey the safety rule: the distance from the back of the car ahead to the front of the car behind is exactly one car length for each 15 kilometers per hour of speed or fraction thereof (Thus the front of a car traveling 52 kilometers per hour will be four car lengths behind the back of the car in front of it.) A photoelectric eye by the side of the road counts the number of cars that pass in one hour. Assuming that each car is 4 meters long and that the cars can travel at any speed, let $M$ be the maximum whole number of cars that can pass the photoelectric eye in one hour. Find the quotient when $M$ is divided by 10.

Problem 13

Let

$p(x,y) = a_0 + a_1x + a_2y + a_3x^2 + a_4xy + a_5y^2 + a_6x^3 + a_7x^2y + a_8xy^2 + a_9y^3$ .

Suppose that

$p(0,0) = p(1,0) = p( - 1,0) = p(0,1) = p(0, - 1) = p(1,1) = p(1, - 1) = p(2,2) = 0$ .

There is a point $left(frac {a}{c},frac {b}{c}right)$ for which $pleft(frac {a}{c},frac {b}{c}right) = 0$ for all such polynomials, where $a$ , $b$ , and $c$ are positive integers, $a$ and $c$ are relatively prime, and $c > 1$ . Find $a + b + c$ .

Problem 14

Let $overline{AB}$ be a diameter of circle $omega$ . Extend $overline{AB}$ through $A$ to $C$ . Point $T$ lies on $omega$ so that line $CT$ is tangent to $omega$ . Point $P$ is the foot of the perpendicular from $A$ to line $CT$ . Suppose $AB = 18$ , and let $m$ denote the maximum possible length of segment $BP$ . Find $m^{2}$ .

Problem 15

A square piece of paper has sides of length $100$ . From each corner a wedge is cut in the following manner: at each corner, the two cuts for the wedge each start at distance $sqrt {17}$ from the corner, and they meet on the diagonal at an angle of $60^circ$ (see the figure below). The paper is then folded up along the lines joining the vertices of adjacent cuts. When the two edges of a cut meet, they are taped together. The result is a paper tray whose sides are not at right angles to the base. The height of the tray, that is, the perpendicular distance between the plane of the base and the plane formed by the upper edges, can be written in the form $sqrt [n]{m}$ , where $m$ and $n$ are positive integers, $m < 1000$ , and $m$ is not divisible by the $n$ th power of any prime. Find $m + n$ .

$[asy]import cse5; size(200); pathpen=black; real s=sqrt(17); real r=(sqrt(51)+s)/sqrt(2); D((0,2*s)--(0,0)--(2*s,0)); D((0,s)--r*dir(45)--(s,0)); D((0,0)--r*dir(45)); D((r*dir(45).x,2*s)--r*dir(45)--(2*s,r*dir(45).y)); MP("30^circ",r*dir(45)-(0.25,1),SW); MP("30^circ",r*dir(45)-(1,0.5),SW); MP("sqrt{17}",(0,s/2),W); MP("sqrt{17}",(s/2,0),S); MP("mathrm{cut}",((0,s)+r*dir(45))/2,N); MP("mathrm{cut}",((s,0)+r*dir(45))/2,E); MP("mathrm{fold}",(r*dir(45).x,s+r/2*dir(45).y),E); MP("mathrm{fold}",(s+r/2*dir(45).x,r*dir(45).y));[/asy]$

2008AIME II详细解析

Extend $AB$ to form a right triangle with legs $6$ and $8$ such that $AD$ is the hypotenuse and connect the points $CD$ so that you have a rectangle. The base $CD$ of the rectangle will be $9+6+6=21$ . Now, let $E$ be the intersection of $BD$ and $AC$ . This means that $triangle ABE$ and $triangle DCE$ are with ratio $frac{21}{9}=frac73$ . Set up a proportion, knowing that the two heights add up to 8. We will let $y$ be the height from $E$ to $DC$ , and $x$ be the height of $triangle ABE$ . $[frac{7}{3}=frac{y}{x}]$ $[frac{7}{3}=frac{8-x}{x}]$ $[7x=24-3x]$ $[10x=24]$ $[x=frac{12}{5}]$ This means that the area is $A=tfrac{1}{2}(9)(tfrac{12}{5})=tfrac{54}{5}$ . This gets us $54+5=boxed{059}.$ -Solution by the Math Wizard, Number Magician of the Second Order, Head of the Council of the GeometersUsing the diagram in Solution 1, let $E$ be the intersection of $BD$ and $AC$ . We can see that angle $C$ is in both $triangle BCE$ and $triangle ABC$ . Since $triangle BCE$ and $triangle ADE$ are congruent by AAS, we can then state $AE=BE$ and $DE=CE$ . It follows that $BE=AE$ and $CE=17-BE$ . We can now state that the area of $triangle ABE$ is the area of $triangle ABC-$ the area of $triangle BCE$ . Using Heron's formula, we compute the area of $triangle ABC=36$ . Using the Law of Cosines on angle $C$ , we obtain $[9^2=17^2+10^2-2(17)(10)cosC]$ $[-308=-340cosC]$ $[cosC=frac{308}{340}]$ (For convenience, we're not going to simplify.)Applying the Law of Cosines on $triangle BCE$ yields $[BE^2=10^2+(17-BE)^2-2(10)(17-BE)cosC]$ $[BE^2=389-34BE+BE^2-20(17-BE)(frac{308}{340})]$ $[0=389-34BE-(340-20BE)(frac{308}{340})]$ $[0=389-34BE+frac{308BE}{17}]$ $[0=81-frac{270BE}{17}]$ $[81=frac{270BE}{17}]$ $[BE=frac{51}{10}]$ This means $CE=17-BE=17-frac{51}{10}=frac{119}{10}$ . Next, apply Heron's formula to get the area of $triangle BCE$ , which equals $frac{126}{5}$ after simplifying. Subtracting the area of $triangle BCE$ from the area of $triangle ABC$ yields the area of $triangle ABE$ , which is $frac{54}{5}$ , giving us our answer, which is $54+5=boxed{059}.$ -Solution by flobszemathguy
$[asy] unitsize(10); pair A = (0,0); pair B = (9,0); pair C = (15,8); pair D = (-6,8); draw(A--B--C--cycle); draw(B--D--A); label("$A$",A,dir(-120)); label("$B$",B,dir(-60)); label("$C$",C,dir(60)); label("$D$",D,dir(120)); label("$9$",(A+B)/2,dir(-90)); label("$10$",(D+A)/2,dir(-150)); label("$10$",(C+B)/2,dir(-30)); label("$17$",(D+B)/2,dir(60)); label("$17$",(A+C)/2,dir(120)); draw(D--(-6,0)--A,dotted); label("$8$",(D+(-6,0))/2,dir(180)); label("$6$",(A+(-6,0))/2,dir(-90)); draw((4.5,0)--(4.5,2.4),dotted); label("$h$", (4.5,1.2), dir(180)); label("$4.5$", (6,0), dir(90)); [/asy]$ - Diagram by Brendanb4321 extended by Duoquinquagintillion

Begin with the first step of solution 1, seeing $AD$ is the hypotenuse of a $6-8-10$ triangle and calling the intersection of $DB$ and $AC$ point $E$ . Next, notice $DB$ is the hypotenuse of an $8-15-17$ triangle. Drop an altitude from $E$ with length $h$ , so the other leg of the new triangle formed has length $4.5$ . Notice we have formed similar triangles, and we can solve for $h$ .

$[frac{h}{4.5} = frac{8}{15}]$ $[h = frac{36}{15} = frac{12}{5}]$

So $triangle ABE$ has area $[frac{ frac{12}{5} cdot 9}{2} = frac{54}{5}]$ And $54+5=boxed{059}.$ - Solution by Duoquinquagintillion

Let $a = angle{CAB}$ . By Law of Consine, $[cos a = frac{17^2+9^2-10^2}{2*9*17} = frac{15}{17}]$ $[sin a = sqrt{1-cos a} = frac{8}{17}]$ $[tan a = frac{8}{15}]$ $[A = frac{1}{2}* 9*frac{9}{2}tan a = frac{54}{5}]$ And $54+5=boxed{059}.$
Let $P_n$ be the probability the frog visits pad $7$ starting from pad $n$ . Then $P_7 = 1$ , $P_6 = frac12$ , and $P_n = frac12(P_{n + 1} + P_{n + 2})$ for all integers $1 leq n leq 5$ . Working our way down, we find $[P_5 = frac{3}{4}]$ $[P_4 = frac{5}{8}]$ $[P_3 = frac{11}{16}]$ $[P_2 = frac{21}{32}]$ $[P_1 = frac{43}{64}]$ $43 + 64 = boxed{107}$ .Define a one jump to be a jump from k to K + 1 and a two jump to be a jump from k to k + 2.Case 1: (6 one jumps) (1/2)^6 = 1/64Case 2: (4 one jumps and 1 two jumps) 5C1 x (1/2)^5 = 5/32Case 3: (2 one jumps and 2 two jumps) 4C2 x (1/2)^4 = 3/8Case 4: (3 two jumps) (1/2)^3 = 1/8
Summing the probabilities gives us 43/64 so the answer is 107.

- pi_is_3.14

Let $P_n$ be the probability that the frog lands on lily pad $n$ . The probability that the frog never lands on pad $n$ is $frac{1}{2}P_{n-1}$ , so $1-P_n=frac{1}{2}P_{n-1}$ . This rearranges to $P_n=1-frac{1}{2}P_{n-1}$ , and we know that $P_1=1$ , so we can compute $P_7$ to be $frac{43}{64}$ , meaning that our answer is $boxed{107}$

-Stormersyle

For any point $n$ , let the probability that the frog lands on lily pad $n$ be $P_n$ . The frog can land at lily pad $n$ with either a double jump from lily pad $n-2$ or a single jump from lily pad $n-1$ . Since the probability when the frog is at $n-2$ to make a double jump is $frac{1}{2}$ and same for when it's at $n-1$ , the recursion is just $P_n = frac{P_{n-2}+P_{n-1}}{2}$ . Using the fact that $P_1 = 1$ , and $P_2 = frac{1}{2}$ , we find that $P_7 = frac{43}{64}$ . $43 + 64 = boxed{107}$
As 71 is prime, $c$ , $d$ , and $e$ must be 1, 1, and 71 (in some order). However, since $c$ and $e$ are divisors of 70 and 72 respectively, the only possibility is $(c,d,e) = (1,71,1)$ . Now we are left with finding the number of solutions $(a,b,f,g)$ satisfying $ab = 70$ and $fg = 72$ , which separates easily into two subproblems. The number of positive integer solutions to $ab = 70$ simply equals the number of divisors of 70 (as we can choose a divisor for $a$ , which uniquely determines $b$ ). As $70 = 2^1 cdot 5^1 cdot 7^1$ , we have $d(70) = (1+1)(1+1)(1+1) = 8$ solutions. Similarly, $72 = 2^3 cdot 3^2$ , so $d(72) = 4 times 3 = 12$ .Then the answer is simply $8 times 12 = boxed{096}$ .
Notice that, other than the number 5, the remaining numbers 1, 2, 3, 4, 6 are only divisible by 2 and/or 3. We can do some cases on the number of 5's rolled (note that there are $6^4 = 1296$ outcomes).Case 1 (easy): Four 5's are rolled. This has probability $frac{1}{6^4}$ of occurring.Case 2: Two 5's are rolled.Case 3: No 5's are rolled.To find the number of outcomes for the latter two cases, we will use recursion. Consider a 5-sided die with faces numbered 1, 2, 3, 4, 6. For $n ge 1$ , let $a_n$ equal the number of outcomes after rolling the die $n$ times, with the property that the product is a square. Thus, $a_1 = 2$ as 1 and 4 are the only possibilities.To find $a_{n+1}$ given $a_n$ (where $n ge 1$ ), we observe that if the first $n$ rolls multiply to a perfect square, then the last roll must be 1 or 4. This gives $2a_n$ outcomes. Otherwise, the first $n$ rolls do not multiply to a perfect square ( $5^n - a_n$ outcomes). In this case, we claim that the last roll is uniquely determined (either 2, 3, or 6). If the product of the first $n$ rolls is $2^x 3^y$ where $x$ and $y$ are not both even, then we observe that if $x$ and $y$ are both odd, then the last roll must be 6; if only $x$ is odd, the last roll must be 2, and if only $y$ is odd, the last roll must be 3. Thus, we have $5^n - a_n$ outcomes in this case, and $a_{n+1} = 2a_n + (5^n - a_n) = 5^n + a_n$ .
Computing $a_2$ , $a_3$ , $a_4$ gives $a_2 = 7$ , $a_3 = 32$ , and $a_4 = 157$ . Thus for Case 3, there are 157 outcomes. For case 2, we multiply by $binom{4}{2} = 6$ to distribute the two 5's among four rolls. Thus the probability is

$[frac{1 + 6 cdot 7 + 157}{6^4} = frac{200}{6^4} = frac{25}{162} implies m+n = boxed{187}]$

-scrabbler94

We can solve this without finding the amount of cases. Notice when we roll a 1 or a 4, it does not affect whether or not the product is a square number. We have a 1/3 chance of rolling either a 1 or 4. We have a 2/3 chance of rolling a 2,3,5 or 6. Lets call rolling 1 or 4 rolling a dud.

Probability of rolling 4 duds: $left(frac{1}{3}right)^4$

Probability of rolling 3 duds: $4 * left(frac{1}{3}right)^3 * frac{2}{3}$

Probability of rolling 2 duds: $6 * left(frac{1}{3}right)^2 * left(frac{2}{3}right)^2$

Probability of rolling 1 dud: $4 * frac{1}{3} * left(frac{2}{3}right)^3$

Probability of rolling 0 duds: $left(frac{2}{3}right)^4$

Now we will find the probability of a square product given we have rolled each amount of duds

Probability of getting a square product given 4 duds: 1

Probability of getting a square product given 3 duds: 0 (you will have 1 non-dud and that's never going to be square)

Probability of getting a square product given 2 duds: $frac{1}{4}$ (as long as our two non-duds are the same, our product will be square)

Probability of getting a square product given 1 duds: $frac{3!}{4^3}$ = $frac{3}{32}$ (the only way to have a square product is rolling a 2,3 and 6. There are 3! ways of doing that and a total of $4^3$ ways to roll 3 non-duds).

Probability of getting a square product given 0 duds: $frac{40}{4^4}$ = $frac{5}{32}$ (We can have any two non-duds twice. For example, 2,2,5,5. There are $binom{4}{2} = 6$ ways of choosing which two non-duds to use and $binom{4}{2} = 6$ ways of choosing how to arrange those 4 numbers. That gives us 6*6=36 combinations. We can also have 2,2,2,2 or 3,3,3,3 or 5,5,5,5 or 6,6,6,6. This gives us a total of 40 combinations).

We multiply each probability of rolling k duds with the probability of getting a square product given k duds and then sum all the values. $[left(frac{1}{3}right)^4 * 1 + 4 * left(frac{1}{3}right)^3 * frac{2}{3} * 0 + 6 * left(frac{1}{3}right)^2 * left(frac{2}{3}right)^2 * frac{1}{4} + 4 * frac{1}{3} * left(frac{2}{3}right)^3 * frac{3}{32} + left(frac{2}{3}right)^4 * frac{5}{32} = frac{25}{162}.]$

$25+162$ = $boxed{187}$

-dnaidu (silverlizard)

Note that rolling a 1/4 will not affect whether or not the product is a perfect square. This means that in order for the product to be a perfect square, all non 1/4 numbers rolled must come in pairs, with the only exception being the triplet 2,3, 6. Now we can do casework:

If there are four 1/4's, then there are $2^4=16$ combinations. If there are three 1/4's, then there are 0 combinations, because the fourth number isn't a square. If there are two 1/4's, there are $2^2=4$ ways to choose the two 1/4's, 4 ways to choose the remaining pair of numbers, and $frac{4!}{2!2!}=6$ ways to arrange, so there are $4cdot 4cdot 6=96$ combinations for this case. If there is one 1/4, then there are 2 ways to choose whether it is a 1 or 4, and the remaining three numbers must be 2, 3, and 6, so there are $4!$ ways to order, meaning there are $2cdot 4!=48$ combinations for this case. Our final case is if there are no 1/4's, in which case we must have two pairs. If the two pairs are of different numbers, then there $binom{4}{2}$ to choose the numbers and $frac{4!}{2!2!}=6$ ways to arrange them, so $6cdot 6=36$ . If all four numbers are the same there are $4$ combinations, so there are $4+36=40$ combinations for this case.

Hence there are $16+0+96+48+40=200$ combinations where the product of the dice is a perfect square, and there are $6^4=1296$ total combinations, so the desired probability is $frac{200}{1296}=frac{25}{162}$ , yielding an answer os $25+162=boxed{187}$ .

-Stormersyle

Another way to solve this problem is to do casework on all the perfect squares from $1^2$ to $36^2$ , and how many ways they can be ordered $1^2$ - $1,1,1,1$ - $1$ way. $2^2$ - $4,1,1,1$ or $2,2,1,1$ - $binom{4}{2}+4=10$ ways. $3^2$ - $3,3,1,1$ - $binom{4}{2}=6$ ways. $4^2$ - $4,4,1,1$ , $2,2,2,2$ , or $2,2,4,1$ - $binom{4}{2}+1+12=19$ ways. $5^2$ - $5,5,1,1$ - $binom{4}{2}=6$ ways. $6^2$ - $6,6,1,1$ , $1,2,3,6$ , $2,3,2,3$ , $3,3,4,1$ - $2*binom{4}{2}+4!+12=48$ ways. $7^2$ - Since there is a prime greater than 6 in its prime factorization there are $0$ ways. $8^2$ - $4,4,4,1$ or $2,4,2,4$ - $binom{4}{2}+4=10$ ways. $9^2$ - $3,3,3,3$ - $1$ way. $10^2$ - $2,2,5,5$ or $1,4,5,5$ - $6+12=18$ ways. $11^2$ - $0$ ways for the same reason as $7^2$ . $12^2$ - $6,6,2,2$ , $4,4,3,3$ , $2,3,4,6$ , or $1,4,6,6$ - $2*binom{4}{2}+4!+12=48$ ways. $13^2$ - $0$ ways. $14^2$ - $0$ ways. $15^2$ - $3,3,5,5$ - $binom{4}{2}=6$ ways. $16^2$ - $4,4,4,4$ - $1$ way. $17^2$ - $0$ ways. $18^2$ - $3,3,6,6$ - $binom{4}{2}=6$ ways. $19^2$ - $0$ ways. $20^2$ - $4,4,5,5$ - $binom{4}{2}=6$ ways. $21^2$ - $0$ ways. $22^2$ - $0$ ways. $23^2$ - $0$ ways. $24^2$ - $4,4,6,6$ - $binom{4}{2}=6$ ways. $25^2$ - $5,5,5,5$ - $1$ way. $26^2$ - $0$ ways. $27^2$ - $0$ ways. $28^2$ - $0$ ways. $29^2$ - $0$ ways. $30^2$ - $5,5,6,6$ - $binom{4}{2}$ ways. $31^2$ - $0$ ways. $32^2$ - $0$ ways. $33^2$ - $0$ ways. $34^2$ - $0$ ways. $35^2$ - $0$ ways. $36^2$ - $6,6,6,6$ - $1$ way.

There are $6^4=1296$ ways that the dice can land. Summing up the ways, it is easy to see that there are $200$ ways. This results in a probability of $frac{200}{1296}=frac{25}{162}impliesboxed{187}$ -superninja2000
There are ambassadors and there are seats for them. So we consider the position of the blank seats. There are kinds of versions: If the two seats are adjacent to each other, there are options, and the ambassadors are sitting in four adjacent seats, and there are five seats that their advisors can sit. Choose any of them and the advisors’ seats are fixed, so there are kinds of solutions for the advisors to sit. And that’s a if we don’t consider the order of the ambassadors. We can also get that if the blank seats are opposite, it will be , if they are not adjacent and not opposite, it will be . So the total is And the remainder is 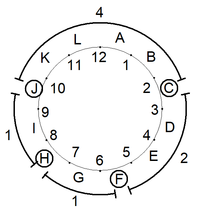In the diagram, the seats are numbered 1...12. Rather than picking seats for each person, however, each ambassador/assistant team picks a gap between the seats (A...L) and the ambassador sits in the even seat while the assistant sits in the odd seat. For example, if team 1 picks gap C then Ambassador 1 will sit in seat 2 while assistant 1 will sit in seat 3. No two teams can pick adjacent gaps. For example, if team 1 chooses gap C then team 2 cannot pick gaps B or D. In the diagram, the teams have picked gaps C, F, H and J. Note that the gap-gaps - distances between the chosen gaps - (in the diagram, 2, 1, 1, 4) must sum to 8. So, to get the number of seatings, we:
1. Choose a gap for team 1 ( $12$ options)
2. Choose 3 other gaps around the table with positive gap-gaps. The number of ways to do this is the number of ways to partition 8 with 4 positive integers. This is the same as partitioning 4 with 4 non-negative integers, and using stars-and-bars, this is $dbinom{4+4-1}{4-1}=dbinom{7}{3}=35$
3. Place the other 3 teams in the chosen gaps ( $6$ permutations)
So the total is $12cdot35cdot6=2520$ And the remainder is $boxed{520}$

There are $360cdot16$ total ways to let everyone sit. However this may lead to advisors sitting in the same chair, leading to awkward situations. So we find how many ways this happens. There are 6 ways to choose which advisors end up sitting together, times 12 ways to find neighboring even seats and sitting down, 12 ways for the rest of the ambassador to sit, and 4 ways for their advisors to sit to get 3456 ways for this to happen. However we overcounted the case when two pairs of advisors run out of room to sit, where there are $6cdot9cdot4=216$ ways to happen. So 5760-3456+216= $2boxed{520}$ .
Using change of base on the second equation to base b, $[frac{log x}{log log x }=54]$ $[log x = 54 cdot log log x]$ $[b^{log x} = b^{54 log log x}]$ $[x = (b^{log log x})^{54}]$ $[x = (log x)^{54}]$ Substituting this into the $sqrt x$ of the first equation, $[3log((log x)^{27}log x) = 56]$ $[3log(log x)^{28} = 56]$ $[log(log x)^{84} = 56]$ We can manipulate this equation to be able to substitute $x = (log x)^{54}$ a couple more times: $[log(log x)^{54} = 56 cdot frac{54}{84}]$ $[log x = 36]$ $[(log x)^{54} = 36^{54}]$ $[x = 6^{108}]$ However, since we found that $log x = 36$ , $x$ is also equal to $b^{36}$ . Equating these, $[b^{36} = 6^{108}]$ $[b = 6^3 = boxed{216}]$ We start by simplifying the first equation to $[3log(sqrt{x}log x)=log(x^{frac{3}{2}}log^3x)=56]$ $[x^frac{3}{2}cdot log_b^3x=b^{56}]$ Next, we simplify the second equation to $[log_{log(x)}(x)=frac{log_b(x)}{log_b(log_b(x))}=54]$ $[log_bx=54log_b(log_b(x))=log_b(log_b^{54}(x))]$ $[x=log_b^{54}x]$ Substituting this into the first equation gives $[log_b^{54cdot frac{3}{2}}(x)cdot log_b^3x=log_b^{84}x=b^{56}]$ $[x=b^{b^{frac{56}{84}}}=b^{b^{frac{2}{3}}}]$ Plugging this into $x=log_b^{54}x$ gives $[b^{b^{frac{2}{3}}}=log_b^{54}(b^{b^frac{2}{3}})=b^{frac{2}{3}cdot 54}=b^{36}]$ $[b^{frac{2}{3}}=36]$ $[b=36^{frac{3}{2}}=6^3=boxed{216}]$ -ktongApply change of base to $[log_{log x}(x)=54]$ to yield: $[frac{log_b(x)}{log_b(log_b(x))}=54]$ which can be rearranged as: $[frac{log_b(x)}{54}=log_b(log_b(x))]$ Apply log properties to $[3log(sqrt{x}log x)=56]$ to yield: $[3(frac{1}{2}log_b(x)+log_b(log_b(x)))=56Rightarrowfrac{1}{2}log_b(x)+log_b(log_b(x))=frac{56}{3}]$ Substituting $[frac{log_b(x)}{54}=log_b(log_b(x))]$ into the equation $frac{1}{2}log_b(x)+log_b(log_b(x))=frac{56}{3}$ yields: $[frac{1}{2}log_b(x)+frac{log_b(x)}{54}=frac{28log_b(x)}{54}=frac{56}{3}]$ So $[log_b(x)=36.]$ Substituting this back in to $[frac{log_b(x)}{54}=log_b(log_b(x))]$ yields $[frac{36}{54}=log_b(36).]$ So, $[b^{frac{2}{3}}=36Rightarrow boxed{b=216}]$ -Ghazt2002
1st equation: $[log (sqrt{x}log x)=frac{56}{3}]$ $[log(sqrt x)+log(log x)=frac{1}{2}log x+log(log x)=frac{56}{3}]$ 2nd equation: $[x=(log x)^{54}]$ So now substitute $log x=a$ and $x=b^a$ : $[b^a=a^{54}]$ $[b=a^{frac{54}{a}}]$ We also have that $[frac{1}{2}a+log_{a^frac{54}{a}} a=frac{56}{3}]$ $[frac{1}{2}a+frac{1}{54}a=frac{56}{3}]$ This means that $frac{14}{27}a=frac{56}{3}$ , so $[a=36]$ $[b=36^{frac{54}{36}}=36^frac{3}{2}=boxed{216}]$ .

-Stormersyle

Let $y = log _{b} x$ Then we have $[3log _{b} (ysqrt{x}) = 56]$ $[log _{y} x = 54]$ which gives $[y^{54} = x]$ Plugging this in gives $[3log _{b} (y * y^{27}) = 3log _{b} y^{28} = 56]$ which gives $[log _{b} y = dfrac{2}{3}]$ so $[b^{2/3} = y]$ By substitution we have $[b^{36} = x]$ which gives $[y = log _{b} x = 36]$ Plugging in again we get $[b = 36^{3/2} = fbox{216}]$
Let the points of intersection of $ell_a, ell_b,ell_c$ with $triangle ABC$ divide the sides into consecutive segments $BD,DE,EC,CF,FG,GA,AH,HI,IB$ . Furthermore, let the desired triangle be $triangle XYZ$ , with $X$ closest to side $BC$ , $Y$ closest to side $AC$ , and $Z$ closest to side $AB$ . Hence, the desired perimeter is $XE+EF+FY+YG+GH+HZ+ZI+ID+DX=(DX+XE)+(FY+YG)+(HZ+ZI)+115$ since $HG=55$ , $EF=15$ , and $ID=45$ .Note that $triangle AHGsim triangle BIDsim triangle EFCsim triangle ABC$ , so using similar triangle ratios, we find that $BI=HA=30$ , $BD=HG=55$ , $FC=frac{45}{2}$ , and $EC=frac{55}{2}$ .We also notice that $triangle EFCsim triangle YFGsim triangle EXD$ and $triangle BIDsim triangle HIZ$ . Using similar triangles, we get that $[FY+YG=frac{GF}{FC}cdot left(EF+ECright)=frac{225}{45}cdot left(15+frac{55}{2}right)=frac{425}{2}]$ $[DX+XE=frac{DE}{EC}cdot left(EF+FCright)=frac{275}{55}cdot left(15+frac{45}{2}right)=frac{375}{2}]$ $[HZ+ZI=frac{IH}{BI}cdot left(ID+BDright)=2cdot left(45+55right)=200]$ Hence, the desired perimeter is $200+frac{425+375}{2}+115=600+115=boxed{715}$ -ktong
We have $frac{1+sqrt{3}i}{2} = omega$ where $omega = e^{frac{ipi}{3}}$ is a primitive 6th root of unity. Then we have $begin{align*} f(omega) &= aomega^{2018} + bomega^{2017} + comega^{2016}\ &= aomega^2 + bomega + c end{align*}$ We wish to find $f(1) = a+b+c$ . We first look at the real parts. As $text{Re}(omega^2) = -frac{1}{2}$ and $text{Re}(omega) = frac{1}{2}$ , we have $-frac{1}{2}a + frac{1}{2}b + c = 2015 implies -a+b + 2c = 4030$ . Looking at imaginary parts, we have $text{Im}(omega^2) = text{Im}(omega) = frac{sqrt{3}}{2}$ , so $frac{sqrt{3}}{2}(a+b) = 2019sqrt{3} implies a+b = 4038$ . As $a$ and $b$ do not exceed 2019, we must have $a = 2019$ and $b = 2019$ . Then $c = frac{4030}{2} = 2015$ , so $f(1) = 4038 + 2015 = 6053 implies f(1) pmod{1000} = boxed{53}$ .
Every 20-pretty integer can be written in form $n = 2^a 5^b k$ , where $a ge 2$ , $b ge 1$ , $gcd(k,10) = 1$ , and $d(n) = 20$ , where $d(n)$ is the number of divisors of $n$ . Thus, we have $20 = (a+1)(b+1)d(k)$ , using the fact that the divisor function is multiplicative. As $(a+1)(b+1)$ must be a divisor of 20, there are not many cases to check.If $a+1 = 4$ , then $b+1 = 5$ . But this leads to no solutions, as $(a,b) = (3,4)$ gives $2^3 5^4 > 2019$ .If $a+1 = 5$ , then $b+1 = 2$ or $4$ . The first case gives $n = 2^4 cdot 5^1 cdot p$ where $p$ is a prime other than 2 or 5. Thus we have $80p < 2019 implies p = 3, 7, 11, 13, 17, 19, 23$ . The sum of all such $n$ is $80(3+7+11+13+17+19+23) = 5760$ . In the second case $b+1 = 4$ and $d(k) = 1$ , and there is one solution $n = 2^4 cdot 5^3 = 2000$ .If $a+1 = 10$ , then $b+1 = 2$ , but this gives $2^9 cdot 5^1 > 2019$ . No other values for $a+1$ work.Then we have $frac{S}{20} = frac{80(3+7+11+13+17+19+23) + 2000}{20} = 372 + 100 = boxed{472}$ .
Note that if $tan theta$ is positive, then $theta$ is in the first or third quadrant, so $0^{circ} < theta < 90^{circ} pmod{180^{circ}}$ . Also notice that the only way $tan{left(2^{n}thetaright)}$ can be positive for all $n$ that are multiples of $3$ is when $2^0theta, 2^3theta, 2^6theta$ , etc. are all the same value $pmod{180^{circ}}$ . This happens if $8theta = theta pmod{180^{circ}}$ , so $7theta = 0^{circ} pmod{180^{circ}}$ . Therefore, the only possible values of theta between $0^{circ}$ and $90^{circ}$ are $frac{180}{7}^{circ}$ , $frac{360}{7}^{circ}$ , and $frac{540}{7}^{circ}$ . However $frac{180}{7}^{circ}$ does not work since $tan{2 cdot frac{180}{7}^{circ}}$ is positive, and $frac{360}{7}^{circ}$ does not work because $tan{4 cdot frac{360}{7}^{circ}}$ is positive. Thus, $theta = frac{540}{7}^{circ}$ . $540 + 7 = boxed{547}$ .As in the previous solution, we note that $tan theta$ is positive when $theta$ is in the first or third quadrant. In order for $tanleft(2^nthetaright)$ to be positive for all $n$ divisible by $3$ , we must have $theta$ , $2^3theta$ , $2^6theta$ , etc to lie in the first or second quadrants. We already know that $thetain(0,90)$ . We can keep track of the range of $2^ntheta$ for each $n$ by considering the portion in the desired quadrants, which gives $[n=1 implies (90,180)]$ $[n=2implies (270,360)]$ $[n=3 implies (180,270)]$ $[n=4 implies (90,180)]$ $[n=5implies(270,360)]$ $[n=6 implies (180,270)]$ $[cdots]$ at which point we realize a pattern emerging. Specifically, the intervals repeat every $3$ after $n=1$ . We can use these repeating intervals to determine the desired value of $theta$ since the upper and lower bounds will converge to such a value (since it is unique, as indicated in the problem). Let's keep track of the lower bound.Initially, the lower bound is $0$ (at $n=0$ ), then increases to $frac{90}{2}=45$ at $n=1$ . This then becomes $45+frac{45}{2}$ at $n=2$ , $45+frac{45}{2}$ at $n=3$ , $45+frac{45}{2}+frac{45}{2^3}$ at $n=4$ , $45+frac{45}{2}+frac{45}{2^3}+frac{45}{2^4}$ at $n=5$ . Due to the observed pattern of the intervals, the lower bound follows a partial geometric series. Hence, as $n$ approaches infinity, the lower bound converges to $[sum_{k=0}^{infty}left(45+frac{45}{2}right)cdot left(frac{1}{8}right)^k=frac{45+frac{45}{2}}{1-frac{1}{8}}=frac{frac{135}{2}}{frac{7}{8}}=frac{540}{7}implies p+q=540+7=boxed{547}]$ -ktongSince $tanleft(thetaright) > 0$ , $0 < theta < 90$ . Since $tanleft(2thetaright) < 0$ , $theta$ has to be in the second half of the interval (0, 90) ie (45, 90). Since $tanleft(4thetaright) < 0$ , $theta$ has to be in the second half of that interval ie (67.5, 90). And since $tanleft(8thetaright) > 0$ , $theta$ has to be in the first half of (67.5, 90). Inductively, the pattern repeats: $theta$ is in the first half of the second half of the second half of the first half of the second half of the second half... of the interval (0, 90). Consider the binary representation of numbers in the interval (0, 1). Numbers in the first half of the interval start with 0.0... and numbers in the second half start with 0.1... . Similarly, numbers in the second half of the second half start with 0.11... etc. So if we want a number in the first half of the second half of the second half... of the interval, we want its binary representation to be $0.11011011011..._2 = frac{6}{7}_{10}$ . So we want the number which is 6/7 of the way through the interval (0, 90) so $theta = frac{6}{7}cdot 90 = frac{540}{7}$ and $p+q = 540 + 7 = boxed{547}$ With some simple arithmetic and guess and check, we can set the lower bound and upper bounds for the "first round of $3$ powers of two", which are $frac{540}{8} = 67.5$ and $frac{630}{8} = 78.75$ . Going on to the "second round of $3$ powers of two, we set the new lower and upper bounds as $frac{360 times 12.5}{64} = 70.3125$ and $frac{360 times 13.75}{64} = 77.34375$ using some guess and check and bashing. Now, it is obvious that the bounds for the "zeroth round of $3$ powers of two" are $0$ and $90$ , and notice that $90 - 78.75 = 11.25$ and $78.75 - 77.34375 = 1.40625$ and $frac{11.25}{1.40625} = 8$ . This is obviously a geometric series, so setting $11.25$ as $u$ , we obtain $90 - (u + frac{u}{8} + frac{u}{64} + ...)$ = $90 - frac{u}{1-frac{1}{8}}$ = $frac{u}{frac{7}{8}}$ = $frac{45}{4} times frac{8}{7}$ which simplifies to $frac{90}{7}$ . We can now finally subtract $frac{90}{7}$ from $frac{630}{7}$ and then we get $frac{540}{7}$ as the unique angle, so $boxed{547}$ is our answer. -fidgetboss_4000
Note that from the tangency condition that the supplement of $angle CAB$ with respects to lines $AB$ and $AC$ are equal to $angle AKB$ and $angle AKC$ , respectively, so from tangent-chord, $[angle AKC=angle AKB=180^{circ}-angle BAC]$ Also note that $angle ABK=angle KAC$ , so $triangle AKBsim triangle CKA$ . Using similarity ratios, we can easily find $[AK^2=BK*KC]$ However, since $AB=7$ and $CA=9$ , we can use similarity ratios to get $[BK=frac{7}{9}AK, CK=frac{9}{7}AK]$ Now we use Law of Cosines on $triangle AKB$ : From reverse Law of Cosines, $cos{angle BAC}=frac{11}{21}implies cos{(180^{circ}-angle BAC)}=-frac{11}{21}$ . This gives us $[AK^2+frac{49}{81}AK^2+frac{22}{27}AK^2=49]$ $[implies frac{196}{81}AK^2=49]$ $[AK=frac{9}{2}]$ so our answer is $9+2=boxed{011}$ . -franchester
If the first term is $x$ , then dividing through by $x$ , we see that we can find the number of progressive sequences whose sum is $frac{360}{x} - 1$ , and whose first term is not 1. If $a(k)$ denotes the number of progressive sequences whose sum is $k$ and whose first term is not 1, then we can express the answer $N$ as follows: $begin{align*}N &= a(359) + a(179) + a(119) + a(89) + a(71) + a(59) + a(44) + a(39) \ &+ a(35) + a(29) + a(23) + a(19) + a(17) + a(14) + a(11) + a(9) \ &+ a(8) + a(7) + a(5) + a(4) + a(3) + a(2) + a(1) + 1 end{align*}$ The $+1$ at the end accounts for the sequence whose only term is 360. Fortunately, many of these numbers are prime; we have $a(p) = 1$ for primes $p$ as the only such sequence is " $p$ " itself. Also, $a(1) = 0$ . So we have $[N = 15 + a(119) + a(44) + a(39) + a(35) + a(14) + a(9) + a(8) + a(4)]$ For small $k$ , $a(k)$ is easy to compute: $a(4) = 1$ , $a(8) = 2$ , $a(9) = 2$ . For intermediate $k$ (e.g. $k=21$ below), $a(k)$ can be computed recursively using previously-computed values of $a(cdot)$ , similar to dynamic programming. Then we have $begin{align*} a(14) &= 1+a(6) = 1+2 = 3\ a(35) &= 1+a(6)+a(4) = 1 + 2 + 1 = 4 \ a(39) &= 2 + a(12) = 2+4 = 6 \ a(44) &= 2 + a(21) + a(10) = 2+4+2=8 \ a(119) &= 1 + a(16) + a(6) = 1 + 3 + 2 = 6 end{align*}$ Thus the answer is $N = 15+6+8+6+4+3+2+2+1 = boxed{47}$ .
This problem is not difficult, but the calculation is tormenting.The actual size of the diagram doesn't matter. To make calculation easier, we discard the original area of the circle, $1$ , and assume the side length of the octagon is $2$ Let $r$ denotes the radius of the circle, $O$ be the center of the circle. $r^2= 1^2 + (sqrt{2}+1)^2= 4+2sqrt{2}$ Now, we need to find the "D"shape, the small area enclosed by one side of the octagon and 1/8 of the circumference of the circle $D= frac{1}{8} pi r^2 - [A_1 A_2 O]=frac{1}{8} pi (4+2sqrt{2})- (sqrt{2}+1)$
Let $PU$ be the height of $triangle A_1 A_2 P$ , $PV$ be the height of $triangle A_3 A_4 P$ , $PW$ be the height of $triangle A_6 A_7 P$ ,

From the 1/7 and 1/9 condition

we have

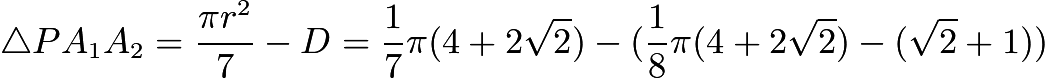
$triangle P A_1 A_2= frac{pi r^2}{7} - D= frac{1}{7} pi (4+2sqrt{2})-(frac{1}{8} pi (4+2sqrt{2})- (sqrt{2}+1))$

$triangle P A_3 A_4= frac{pi r^2}{9} - D= frac{1}{9} pi (4+2sqrt{2})-(frac{1}{8} pi (4+2sqrt{2})- (sqrt{2}+1))$

which gives

$PU= (frac{1}{7}-frac{1}{8}) pi (4+ 2sqrt{2}) + sqrt{2}+1$

$PV= (frac{1}{9}-frac{1}{8}) pi (4+ 2sqrt{2}) + sqrt{2}+1$

Now, let $A_1 A_2$ intersects $A_3 A_4$ at $X$ , $A_1 A_2$ intersects $A_6 A_7$ at $Y$ , $A_6 A_7$ intersects $A_3 A_4$ at $Z$

Clearly, $triangle XYZ$ is an isosceles right triangle, with right angle at $X$

and the height with regard to which shall be $3+2sqrt2$

That $frac{PU}{sqrt{2}} + frac{PV}{sqrt{2}} + PW = 3+2sqrt2$ is a common sense

which gives $PW= 3+2sqrt2-frac{PU}{sqrt{2}} - frac{PV}{sqrt{2}}$

$=3+2sqrt{2}-frac{1}{sqrt{2}}((frac{1}{7}-frac{1}{8}) pi (4+ 2sqrt{2}) + sqrt{2}+1+(frac{1}{9}-frac{1}{8}) pi (4+ 2sqrt{2}) + sqrt{2}+1))$

$=1+sqrt{2}- frac{1}{sqrt{2}}(frac{1}{7}+frac{1}{9}-frac{1}{4})pi(4+2sqrt{2})$

Now, we have the area for $D$ and the area for $triangle P A_6 A_7$

we add them together

$Target Area= frac{1}{8} pi (4+2sqrt{2})- (sqrt{2}+1) + (1+sqrt{2})- frac{1}{sqrt{2}}(frac{1}{7}+frac{1}{9}-frac{1}{4})pi(4+2sqrt{2})$

$=(frac{1}{8} - frac{1}{sqrt{2}}(frac{1}{7}+frac{1}{9}-frac{1}{4}))Total Area$

The answer should therefore be $frac{1}{8}- frac{sqrt{2}}{2}(frac{16}{63}-frac{16}{64})=frac{1}{8}- frac{sqrt{2}}{504}$

The final answer is, therefore, $boxed{504}$

Instead of considering the actual values of the areas, consider only the changes in the areas that result from moving point $P$ from the center of the circle. We will proceed by coordinates. Set the origin at the center of the circle and refer to the following diagram. Note that the area bounded by $overline{A_i}{A_j}$ and the arc $A_iA_j$ is fixed, so we only need to consider the relevant triangles.

$[asy] size(7cm); draw(Circle((0,0),1)); pair P = (0.1,-0.15); filldraw(P--dir(112.5)--dir(112.5-45)--cycle,yellow,red); filldraw(P--dir(112.5-90)--dir(112.5-135)--cycle,yellow,red); filldraw(P--dir(112.5-225)--dir(112.5-270)--cycle,green,red); dot(P); for(int i=0; i<8; ++i) { draw(dir(22.5+45i)--dir(67.5+45i)); draw((0,0)--dir(22.5+45i),gray+dashed); } draw(dir(135)--dir(-45),blue+linewidth(1)); label("$P$", P, dir(-75)); label("$A_1$", dir(112.5), dir(112.5)); label("$A_2$", dir(112.5-45), dir(112.5-45)); label("$A_3$", dir(112.5-90), dir(112.5-90)); label("$A_4$", dir(112.5-135), dir(112.5-135)); label("$A_5$", dir(112.5-180), dir(112.5-180)); label("$A_6$", dir(112.5-225), dir(112.5-225)); label("$A_7$", dir(112.5-270), dir(112.5-270)); label("$A_8$", dir(112.5-315), dir(112.5-315)); dot(dir(112.5)^^dir(112.5-45)^^dir(112.5-90)^^dir(112.5-135)^^dir(112.5-180)^^dir(112.5-225)^^dir(112.5-270)^^dir(112.5-315)); [/asy]$

Define one arbitrary unit as the distance that you need to move $P$ from $A_1A_2$ to change the area of $triangle PA_1A_2$ by $1$ . We can see that $P$ was moved down by $tfrac{1}{7}-tfrac{1}{8}=tfrac{1}{56}$ units to make the area defined by $P$ , $A_1$ , and $A_2$ $tfrac{1}{7}$ . Similarly, $P$ was moved right by $tfrac{1}{8}-tfrac{1}{9}=tfrac{1}{72}$ to make the area defined by $P$ , $A_3$ , and $A_4$ $tfrac{1}{9}$ . This means that $P$ has coordinates $(tfrac{1}{72},-tfrac{1}{56})$ .

Now, we need to consider how this displacement in $P$ affected the area defined by $P$ , $A_6$ , and $A_7$ . This is equivalent to finding the shortest distance between $P$ and the blue line in the diagram (as $K=tfrac{1}{2}bh$ and the blue line represents $h$ while $b$ is fixed). Using an isosceles right triangle, one can find the that shortest distance between $P$ and this line is $tfrac{sqrt{2}}{2}(tfrac{1}{56}-tfrac{1}{72})=tfrac{sqrt{2}}{504}$ .

Remembering the definition of our unit, this yields a final area of $[frac{1}{8}-frac{sqrt{2}}{boxed{504}}.]$
By the Chicken McNugget theorem, the least possible value of $n$ such that $91$ cents cannot be formed satisfies $5n - 5 - n = 91$ , so $n = 24$ . For values of $n$ greater than $24$ , notice that if $91$ cents cannot be formed, then any number $1 bmod 5$ less than $91$ also cannot be formed. The proof of this is that if any number $1 bmod 5$ less than $91$ can be formed, then we could keep adding $5$ cent stamps until we reach $91$ cents. However, since $91$ cents is the greatest postage that cannot be formed, $96$ cents is the first number that is $1 bmod 5$ that can be formed, so it must be formed without any $5$ cent stamps. There are few $(n, n + 1)$ pairs, where $n geq 24$ , that can make $96$ cents. These are cases where one of $n$ and $n + 1$ is a factor of $96$ , which are $(24, 25), (31, 32), (32, 33), (47, 48), (48, 49), (95, 96)$ , and $(96, 97)$ . The last two obviously do not work since $92$ through $94$ cents also cannot be formed, and by a little testing, only $(24, 25)$ and $(47, 48)$ satisfy the condition that $91$ cents is the greatest postage that cannot be formed, so $n = 24, 47$ . $24 + 47 = boxed{071}$ .Notice that once we hit all residues $bmod 5$ , we'd be able to get any number greater (since we can continually add $5$ to each residue). Furthermore, $nnotequiv 0,1pmod{5}$ since otherwise $91$ is obtainable (by repeatedly adding $5$ to either $n$ or $n+1$ ) Since the given numbers are $5$ , $n$ , and $n+1$ , we consider two cases: when $nequiv 4pmod{5}$ and when $n$ is not that.When $nequiv 4 pmod{5}$ , we can only hit all residues $bmod 5$ once we get to $4n$ (since $n$ and $n+1$ only contribute $1$ more residue $bmod 5$ ). Looking at multiples of $4$ greater than $91$ with $nequiv 4pmod{5}$ , we get $n=24$ . It's easy to check that this works. Furthermore, any $n$ greater than this does not work since $91$ isn't the largest unobtainable value (can be verified using Chicken McNugget Theorem).Now, if $nequiv 2,3pmod{5}$ , then we'd need to go up to $2(n+1)=2n+2$ until we can hit all residues $bmod 5$ since $n$ and $n+1$ create $2$ distinct residues $bmod{5}$ . Checking for such $n$ gives $n=47$ and $n=48$ . It's easy to check that $n=47$ works, but $n=48$ does not (since $92$ is unobtainable). Furthermore, any $n$ greater than this does not work since $91$ isn't the largest unobtainable value in those cases (can be verified using Chicken McNugget Theorem).Since we've checked all residues $bmod 5$ , we can be sure that these are all the possible values of $n$ . Hence, the answer is $24+47=boxed{071}$ . - ktongObviously $nle 90$ . We see that the problem's condition is equivalent to: 96 is the smallest number that can be formed which is 1 mod 5, and 92, 93, 94 can be formed (95 can always be formed). Now divide this up into cases. If $nequiv 0pmod{5}$ , then 91 can be formed by using $n+1$ and some 5's, so there are no solutions for this case. If $nequiv 1pmod{5}$ , then 91 can be formed by using $n$ and some 5's, so there are no solutions for this case either.
For $nequiv 2pmod{5}$ , $2n+2$ is the smallest value that can be formed which is 1 mod 5, so $2n+2=96$ and $n=47$ . We see that $92=45+47$ , $93=48+45$ , and $94=47+47$ , so $n=47$ does work. If $nequiv 3pmod{5}$ , then the smallest value that can be formed which is 1 mod 5 is $2n$ , so $2n=96$ and $n=48$ . We see that $94=49+45$ and $93=48+45$ , but 92 cannot be formed, so there are no solutions for this case. If $nequiv 4pmod{5}$ , then we can just ignore $n+1$ since it is a multiple of 5, meaning that the Chicken McNuggest theorem is a both necessary and sufficient condition, and it states that $5n-n-5=91$ meaning $4n=96$ and $n=24$ . Hence, the only two $n$ that work are $n=24$ and $n=47$ , so our answer is $24+47=boxed{071}$ . -Stormersyle
Let $AP=a, AQ=b, cosangle A = k$ Therefore $AB= frac{b}{k} , AC= frac{a}{k}$ By power of point, we have $APcdot BP=XPcdot YP , AQcdot CQ=YQcdot XQ$ Which are simplified to $400= frac{ab}{k} - a^2$ $525= frac{ab}{k} - b^2$ Or
$a^2= frac{ab}{k} - 400$

$b^2= frac{ab}{k} - 525$

(1)

Or

$k= frac{ab}{a^2+400} = frac{ab}{b^2+525}$

Let $u=a^2+400=b^2+525$ Then, $a=sqrt{u-400},b=sqrt{u-525},k=frac{sqrt{(u-400)(u-525)}}{u}$

In triangle $APQ$ , by law of cosine

$25^2= a^2 + b^2 - 2abk$

Pluging (1)

$625= frac{ab}{k} - 400 + frac{ab}{k} - 525 -2abk$

Or

$frac{ab}{k} - abk =775$

Substitute everything by $u$

$u- frac{(u-400)(u-525)}{u} =775$

The quadratic term is cancelled out after simplified

Which gives $u=1400$

Plug back in, $a= sqrt{1000} , b=sqrt{775}$

Then

$ABcdot AC= frac{a}{k} frac{b}{k} = frac{ab}{frac{ab}{u} cdotfrac{ab}{u} } = frac{u^2}{ab} = frac{1400 cdot 1400}{ sqrt{ 1000cdot 875 }} = 560 sqrt{14}$

So the final answer is $560 + 14 = boxed{574}$

By SpecialBeing2017

Let $overline{AP}=a, overline{PB} = b, overline{AQ} = c$ and $overline{QC} = d$

By power of point, we have $overline{AP}cdot overline{PB}=overline{XP}cdot overline{YP}$ and $overline{AQ}cdot overline{QC}=overline{YQ}cdot overline{XQ}$

Therefore, substituting in the values:

$ab = 400$

$cd = 525$

Notice than quadrilateral $BPQC$ is cyclic.

From this fact, we can deduce that $angle PQA= angle B$ and $angle QPA = angle C$

Therefore $triangle ABC$ is similar to $triangle AQP$ .

Therefore: $frac{a}{c+d}=frac{c}{a+b} implies a^2 + ab = c^2 +cd implies a^2 + 400 = c^2 + 525 implies bf{a^2 = c^2 + 125}$

Now using Law of Cosines on $triangle AQP$ we get:

$625 = a^2 + c^2 - 2accos{A}$

Notice $cos{A} = frac{c}{a+b}$

Substituting and Simplifying:

$625 = a^2 + c^2 - 2acfrac{c}{a+b}$

$625 = a^2 + c^2 - 2acfrac{c}{a+frac{400}{a}}$

$625 = c^2 + 125 + c^2 - 2frac{(ac)^2}{a^2+400}$

$625 = c^2 + 125 + c^2 - 2frac{c^2(c^2+125)}{c^2+125+400}$

Now we solve for $c$ using regular algebra which actually turns out to be very easy.

We get $c = 5sqrt{35}$ and from the above relations between the variables we quickly determine $d = 3sqrt{35}$ , $a = 10sqrt{10}$ and $b = 4sqrt{10}$

Therefore $ABcdot AC = (a+b)cdot(c+d) = 560sqrt{14}$

So the answer is $560 + 14 = boxed{574}$