Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2008AIME I真题及答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月9日下午3:29

2008AIME I真题及答案解析

答案解析请参考文末

Problem 1

Of the students attending a school party, $60%$ of the students are girls, and $40%$ of the students like to dance. After these students are joined by $20$ more boy students, all of whom like to dance, the party is now $58%$ girls. How many students now at the party like to dance?

Problem 2

Square $AIME$ has sides of length $10$ units. Isosceles triangle $GEM$ has base $EM$ , and the area common to triangle $GEM$ and square $AIME$ is $80$ square units. Find the length of the altitude to $EM$ in $triangle GEM$ .

Problem 3

Ed and Sue bike at equal and constant rates. Similarly, they jog at equal and constant rates, and they swim at equal and constant rates. Ed covers $74$ kilometers after biking for $2$ hours, jogging for $3$ hours, and swimming for $4$ hours, while Sue covers $91$ kilometers after jogging for $2$ hours, swimming for $3$ hours, and biking for $4$ hours. Their biking, jogging, and swimming rates are all whole numbers of kilometers per hour. Find the sum of the squares of Ed's biking, jogging, and swimming rates.

Problem 4

There exist unique positive integers $x$ and $y$ that satisfy the equation $x^2 + 84x + 2008 = y^2$ . Find $x + y$ .

Problem 5

A right circular cone has base radius $r$ and height $h$ . The cone lies on its side on a flat table. As the cone rolls on the surface of the table without slipping, the point where the cone's base meets the table traces a circular arc centered at the point where the vertex touches the table. The cone first returns to its original position on the table after making $17$ complete rotations. The value of $h/r$ can be written in the form $msqrt {n}$ , where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. Find $m + n$ .

Problem 6

A triangular array of numbers has a first row consisting of the odd integers $1,3,5,ldots,99$ in increasing order. Each row below the first has one fewer entry than the row above it, and the bottom row has a single entry. Each entry in any row after the top row equals the sum of the two entries diagonally above it in the row immediately above it. How many entries in the array are multiples of $67$ ?

Problem 7

Let $S_i$ be the set of all integers $n$ such that $100ileq n < 100(i + 1)$ . For example, $S_4$ is the set ${400,401,402,ldots,499}$ . How many of the sets $S_0, S_1, S_2, ldots, S_{999}$ do not contain a perfect square?

Problem 8

Find the positive integer $n$ such that

$[arctanfrac {1}{3} + arctanfrac {1}{4} + arctanfrac {1}{5} + arctanfrac {1}{n} = frac {pi}{4}.]$

Problem 9

Ten identical crates each of dimensions $3$ ft $times$ $4$ ft $times$ $6$ ft. The first crate is placed flat on the floor. Each of the remaining nine crates is placed, in turn, flat on top of the previous crate, and the orientation of each crate is chosen at random. Let $frac {m}{n}$ be the probability that the stack of crates is exactly $41$ ft tall, where $m$ and $n$ are relatively prime positive integers. Find $m$ .

Problem 10

Let $ABCD$ be an isosceles trapezoid with $overline{AD}||overline{BC}$ whose angle at the longer base $overline{AD}$ is $dfrac{pi}{3}$ . The diagonals have length $10sqrt {21}$ , and point $E$ is at distances $10sqrt {7}$ and $30sqrt {7}$ from vertices $A$ and $D$ , respectively. Let $F$ be the foot of the altitude from $C$ to $overline{AD}$ . The distance $EF$ can be expressed in the form $msqrt {n}$ , where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. Find $m + n$ .

Problem 11

Consider sequences that consist entirely of $A$ 's and $B$ 's and that have the property that every run of consecutive $A$ 's has even length, and every run of consecutive $B$ 's has odd length. Examples of such sequences are $AA$ , $B$ , and $AABAA$ , while $BBAB$ is not such a sequence. How many such sequences have length 14?

Problem 12

On a long straight stretch of one-way single-lane highway, cars all travel at the same speed and all obey the safety rule: the distance from the back of the car ahead to the front of the car behind is exactly one car length for each 15 kilometers per hour of speed or fraction thereof (Thus the front of a car traveling 52 kilometers per hour will be four car lengths behind the back of the car in front of it.) A photoelectric eye by the side of the road counts the number of cars that pass in one hour. Assuming that each car is 4 meters long and that the cars can travel at any speed, let $M$ be the maximum whole number of cars that can pass the photoelectric eye in one hour. Find the quotient when $M$ is divided by 10.

Problem 13

Let

$p(x,y) = a_0 + a_1x + a_2y + a_3x^2 + a_4xy + a_5y^2 + a_6x^3 + a_7x^2y + a_8xy^2 + a_9y^3$ .

Suppose that

$p(0,0) = p(1,0) = p( - 1,0) = p(0,1) = p(0, - 1) = p(1,1) = p(1, - 1) = p(2,2) = 0$ .

There is a point $left(frac {a}{c},frac {b}{c}right)$ for which $pleft(frac {a}{c},frac {b}{c}right) = 0$ for all such polynomials, where $a$ , $b$ , and $c$ are positive integers, $a$ and $c$ are relatively prime, and $c > 1$ . Find $a + b + c$ .

Problem 14

Let $overline{AB}$ be a diameter of circle $omega$ . Extend $overline{AB}$ through $A$ to $C$ . Point $T$ lies on $omega$ so that line $CT$ is tangent to $omega$ . Point $P$ is the foot of the perpendicular from $A$ to line $CT$ . Suppose $AB = 18$ , and let $m$ denote the maximum possible length of segment $BP$ . Find $m^{2}$ .

Problem 15

A square piece of paper has sides of length $100$ . From each corner a wedge is cut in the following manner: at each corner, the two cuts for the wedge each start at distance $sqrt {17}$ from the corner, and they meet on the diagonal at an angle of $60^circ$ (see the figure below). The paper is then folded up along the lines joining the vertices of adjacent cuts. When the two edges of a cut meet, they are taped together. The result is a paper tray whose sides are not at right angles to the base. The height of the tray, that is, the perpendicular distance between the plane of the base and the plane formed by the upper edges, can be written in the form $sqrt [n]{m}$ , where $m$ and $n$ are positive integers, $m < 1000$ , and $m$ is not divisible by the $n$ th power of any prime. Find $m + n$ .

$[asy]import cse5; size(200); pathpen=black; real s=sqrt(17); real r=(sqrt(51)+s)/sqrt(2); D((0,2*s)--(0,0)--(2*s,0)); D((0,s)--r*dir(45)--(s,0)); D((0,0)--r*dir(45)); D((r*dir(45).x,2*s)--r*dir(45)--(2*s,r*dir(45).y)); MP("30^circ",r*dir(45)-(0.25,1),SW); MP("30^circ",r*dir(45)-(1,0.5),SW); MP("sqrt{17}",(0,s/2),W); MP("sqrt{17}",(s/2,0),S); MP("mathrm{cut}",((0,s)+r*dir(45))/2,N); MP("mathrm{cut}",((s,0)+r*dir(45))/2,E); MP("mathrm{fold}",(r*dir(45).x,s+r/2*dir(45).y),E); MP("mathrm{fold}",(s+r/2*dir(45).x,r*dir(45).y));[/asy]$

Say that there were $3k$ girls and $2k$ boys at the party originally. $2k$ like to dance. Then, there are $3k$ girls and $2k + 20$ boys, and $2k + 20$ like to dance.Thus, $dfrac{3k}{5k + 20} = dfrac{29}{50}$ , solving gives $k = 116$ . Thus, the number of people that like to dance is $2k + 20 = boxed{252}$ .Let the number of girls be $g$ . Let the number of total people originally be $t$ .We know that $frac{g}{t}=frac{3}{5}$ from the problem.We also know that $frac{g}{t+20}=frac{29}{50}$ from the problem.We now have a system and we can solve.The first equation becomes: $3t=5g$ .
The second equation becomes:

$50g=29t+580$

Now we can sub in $30t=50g$ by multiplying the first equation by $10$ . We can plug this into our second equation.

$30t=29t+580$

$t=580$

We know that there were originally $580$ people. Of those, $frac{2}{5}*580=232$ like to dance.

We also know that with these people, $20$ boys joined, all of whom like to dance. We just simply need to add $20$ to get $232+20=boxed{252}$

Let $p$ denote the total number of people at the party. Then, because we know the proportions of boys to $p$ both before and after 20 boys arrived, we can create the following equation: $[0.4p+20 = 0.42(p+20)]$ Solving for p gives us $p=580$ , so the solution is $0.4p+20 = boxed{252}$
Note that if the altitude of the triangle is at most $10$ , then the maximum area of the intersection of the triangle and the square is $5cdot10=50$ . This implies that vertex G must be located outside of square $AIME$ . $[asy] pair E=(0,0), M=(10,0), I=(10,10), A=(0,10); draw(A--I--M--E--cycle); pair G=(5,25); draw(G--E--M--cycle); label("(G)",G,N); label("(A)",A,NW); label("(I)",I,NE); label("(M)",M,NE); label("(E)",E,NW); label("(10)",(M+E)/2,S); [/asy]$ Let $GE$ meet $AI$ at $X$ and let $GM$ meet $AI$ at $Y$ . Clearly, $XY=6$ since the area of trapezoid $XYME$ is $80$ . Also, $triangle GXY sim triangle GEM$ .Let the height of $GXY$ be $h$ . By the similarity, $dfrac{h}{6} = dfrac{h + 10}{10}$ , we get $h = 15$ . Thus, the height of $GEM$ is $h + 10 = boxed{025}$ .
Let the biking rate be $b$ , swimming rate be $s$ , jogging rate be $j$ , all in km/h.We have $2b + 3j + 4s = 74,2j + 3s + 4b = 91$ . Subtracting the second from twice the first gives $4j + 5s = 57$ . Mod 4, we need $sequiv1pmod{4}$ . Thus, $(j,s) = (13,1),(8,5),(3,9)$ . $(13,1)$ and $(3,9)$ give non-integral $b$ , but $(8,5)$ gives $b = 15$ . Thus, our answer is $15^{2} + 8^{2} + 5^{2} = boxed{314}$ .Let $b$ , $j$ , and $s$ be the biking, jogging, and swimming rates of the two people. Hence, $2b + 3j + 4s = 74$ and $4b + 2j + 3s = 91$ . Subtracting gives us that $2b - j - s = 17$ . Adding three times this to the first equation gives that $8b + s = 125implies ble 15$ . Adding four times the previous equation to the first given one gives us that $10b - j = 142implies b > 14implies bge 15$ . This gives us that $b = 15$ , and then $j = 8$ and $s = 5$ . Therefore, $b^2 + s^2 + j^2 = 225 + 64 + 25 = boxed{314}$ .
Completing the square, $y^2 = x^2 + 84x + 2008 = (x+42)^2 + 244$ . Thus $244 = y^2 - (x+42)^2 = (y - x - 42)(y + x + 42)$ by difference of squares.Since $244$ is even, one of the factors is even. A parity check shows that if one of them is even, then both must be even. Since $244 = 2^2 cdot 61$ , the factors must be $2$ and $122$ . Since $x,y > 0$ , we have $y - x - 42 = 2$ and $y + x + 42 = 122$ ; the latter equation implies that $x + y = boxed{080}$ .Indeed, by solving, we find $(x,y) = (18,62)$ is the unique solution.We complete the square like in the first solution: $y^2 = (x+42)^2 + 244$ . Since consecutive squares differ by the consecutive odd numbers, we note that $y$ and $x+42$ must differ by an even number. We can use casework with the even numbers, starting with $y-(x+42)=2$ . $begin{align*}2(x+42)+1+2(x+42)+3&=244 Leftrightarrow x&=18end{align*}$ Thus, $y=62$ and the answer is $boxed{080}$ .We see that $y^2 equiv x^2 + 4 pmod{6}$ . By quadratic residues, we find that either $x equiv 0, 3 pmod{6}$ . Also, $y^2 equiv (x+42)^2 + 244 equiv (x+2)^2 pmod{4}$ , so $x equiv 0, 2 mod{4}$ . Combining, we see that $x equiv 0 mod{6}$ .Testing $x = 6$ and other multiples of $6$ , we quickly find that $x = 18, y = 62$ is the solution. $18+62=boxed{080}$ We solve for x: $x^2 + 84x + 2008-y^2 = 0$
$x=dfrac{-84+sqrt{84^2-4cdot 2008+4y^2}}{2}=-42+sqrt{y^2-244}$

So $y^2-244$ is a perfect square. Since 244 is even, the difference $sqrt{y^2-244} -y^2$ is even, so we try $y^2-244=(y-2)^2$ : $-244=-4y+4$ , $y=62$ .

Plugging into our equation, we find that $x=18$ , and $(x,y)=(18,62)$ indeed satisfies the original equation. $x+y=boxed{080}$

Let $y=x+d$ for some $d>0$ , substitute into the original equation to get $84x + 2008 = 2xd + d^2$ .

All terms except for the last one are even, hence $d^2$ must be even, hence let $d=2e$ . We obtain $21x + 502 = xe + e^2$ . Rearrange to $502-e^2 = x(e-21)$ .

Obviously for $0<e<21$ the right hand side is negative and the left hand side is positive. Hence $egeq 21$ . Let $e=21+f$ , then $fgeq 0$ .

We have $502 - (21+f)^2 = xf$ . Left hand side simplifies to $61 - 42f + f^2$ . As $x$ must be an integer, $f$ must divide the left hand side. But $61$ is a prime, which only leaves two options: $f=1$ and $f=61$ .

Option $f=61$ gives us a negative $x$ . Option $f=1$ gives us $x=61/f - 42 + f = 18$ , and $y = x + d= x + 2e = x + 2(21+f) = 18 + 44 = 62$ , hence $x+y=boxed{080}$ .
The path is a circle with radius equal to the slant height of the cone, which is $sqrt {r^{2} + h^{2}}$ . Thus, the length of the path is $2pisqrt {r^{2} + h^{2}}$ .Also, the length of the path is 17 times the circumference of the base, which is $34rpi$ . Setting these equal gives $sqrt {r^{2} + h^{2}} = 17r$ , or $h^{2} = 288r^{2}$ . Thus, $dfrac{h^{2}}{r^{2}} = 288$ , and $dfrac{h}{r} = 12sqrt {2}$ , giving an answer of $12 + 2 = boxed{014}$ .
Let the $k$ th number in the $n$ th row be $a(n,k)$ . Writing out some numbers, we find that $a(n,k) = 2^{n-1}(n+2k-2)$ .^[1]We wish to find all $2008AIME I真题及答案解析$ such that $67| a(n,k) = 2^{n-1} (n+2k-2)$ . Since $2^{n-1}$ and $67$ are relatively prime, it follows that $67|n+2k-2$ . Since every row has one less element than the previous row, $1 le k le 51-n$ (the first row has $50$ elements, the second $49$ , and so forth; so $k$ can range from $1$ to $50$ in the first row, and so forth). Hence $n+2k-2 le n + 2(51-n) - 2 = 100 - n le 100,$ it follows that $67| n - 2k + 2$ implies that $n-2k+2 = 67$ itself.Now, note that we need $n$ to be odd, and also that $n+2k-2 = 67 le 100-n Longrightarrow n le 33$ .We can check that all rows with odd $n$ satisfying $1 le n le 33$ indeed contains one entry that is a multiple of $67$ , and so the answer is $frac{33+1}{2} = boxed{017}$ .^ Proof: Indeed, note that $2008AIME I真题及答案解析$ , which is the correct formula for the first row. We claim the result by induction on $n$ . By definition of the array, $a(n,k) = a(n-1,k)+a(n-1,k+1)$ , and by our inductive hypothesis, $begin{align*}a(n,k) &= a(n-1,k)+a(n-1,k+1) &= 2^{n-2}(n-1+2k-2)+2^{n-2}(n-1+2(k+1)-2)&=2^{n-2}(2n+4k-4)&=2^{n-1}(n+2k-2)end{align*}$ thereby completing our induction.The result above is fairly intuitive if we write out several rows and then divide all numbers in row $r$ by $2^{r-1}$ (we can do this because dividing by a power of 2 doesn't affect divisibility by $67$ ). The second row will be $2, 4, 6, cdots , 98$ , the third row will be $3, 5, cdots, 97$ , and so forth. Clearly, only the odd-numbered rows can have a term divisible by $67$ . However, with each row the row will have one less element, and the $99-67+1 = 33$ rd row is the last time $67$ will appear. Therefore the number of multiples of 67 in the entire array is $frac{33+1}{2} = boxed{017}$ .
The difference between consecutive squares is $(x + 1)^2 - x^2 = 2x + 1$ , which means that all squares above $50^2 = 2500$ are more than $100$ apart.Then the first $26$ sets ( $S_0,cdots S_{25}$ ) each have at least one perfect square. Also, since $316^2 < 100000$ (which is when $i = 1000$ ), there are $316 - 50 = 266$ other sets after $S_{25}$ that have a perfect square.There are $1000 - 266 - 26 = boxed{708}$ sets without a perfect square.
Since we are dealing with acute angles, $tan(arctan{a}) = a$ .Note that $tan(arctan{a} + arctan{b}) = dfrac{a + b}{1 - ab}$ , by tangent addition. Thus, $arctan{a} + arctan{b} = arctan{dfrac{a + b}{1 - ab}}$ .Applying this to the first two terms, we get $arctan{dfrac{1}{3}} + arctan{dfrac{1}{4}} = arctan{dfrac{7}{11}}$ .Now, $arctan{dfrac{7}{11}} + arctan{dfrac{1}{5}} = arctan{dfrac{23}{24}}$ .We now have $arctan{dfrac{23}{24}} + arctan{dfrac{1}{n}} = dfrac{pi}{4} = arctan{1}$ . Thus, $dfrac{dfrac{23}{24} + dfrac{1}{n}}{1 - dfrac{23}{24n}} = 1$ ; and simplifying, $23n + 24 = 24n - 23 Longrightarrow n = boxed{047}$ .From the expansion of $e^{iA}e^{iB}e^{iC}e^{iD}$ , we can see that $[cos(A + B + C + D) = cos A cos B cos C cos D - tfrac{1}{4} sum_{rm sym} sin A sin B cos C cos D + sin A sin B sin C sin D,]$ and $[sin(A + B + C + D) = sum_{rm cyc}sin A cos B cos C cos D - sum_{rm cyc} sin A sin B sin C cos D .]$ If we divide both of these by $cos A cos B cos C cos D$ , then we have $[tan(A + B + C + D) = frac {1 - sum tan A tan B + tan A tan B tan C tan D}{sum tan A - sum tan A tan B tan C},]$ which makes for more direct, less error-prone computations. Substitution gives the desired answer.Adding a series of angles is the same as multiplying the complex numbers whose arguments they are. In general, $arctanfrac{1}{n}$ , is the argument of $n+i$ . The sum of these angles is then just the argument of the product $[(3+i)(4+i)(5+i)(n+i)]$
and expansion give us $(48n-46)+(48+46n)i$ . Since the argument of this complex number is $frac{pi}{4}$ , its real and imaginary parts must be equal. So we set them equal and expand the product to get $48n - 46 = 48 + 46n.$ Therefore, $n$ equals $boxed{047}$ .
Only the heights matter, and each crate is either 3, 4, or 6 feet tall with equal probability. We have the following: $begin{align*}3a + 4b + 6c &= 41 a + b + c &= 10end{align*}$ Subtracting 3 times the second from the first gives $b + 3c = 11$ , or $(b,c) = (2,3),(5,2),(8,1),(11,0)$ . The last doesn't work, obviously. This gives the three solutions $(a,b,c) = (5,2,3),(3,5,2),(1,8,1)$ . In terms of choosing which goes where, the first two solutions are analogous.For $(5,2,3),(3,5,2)$ , we see that there are $2cdotdfrac{10!}{5!2!3!} = 10cdot9cdot8cdot7$ ways to stack the crates. For $(1,8,1)$ , there are $2dbinom{10}{2} = 90$ . Also, there are $3^{10}$ total ways to stack the crates to any height.Thus, our probability is $dfrac{10cdot9cdot8cdot7 + 90}{3^{10}} = dfrac{10cdot8cdot7 + 10}{3^{8}} = dfrac{570}{3^8} = dfrac{190}{3^{7}}$ . Our answer is the numerator, $boxed{190}$ .
$[asy] size(300); defaultpen(1); pair A=(0,0), D=(4,0), B= A+2 expi(1/3*pi), C= D+2expi(2/3*pi), E=(-4/3,0), F=(3,0); draw(F--C--B--A); draw(E--A--D--C); draw(A--C,dashed); draw(circle(A,abs(C-A)),dotted); label("(A)",A,S); label("(B)",B,NW); label("(C)",C,NE); label("(D)",D,SE); label("(E)",E,N); label("(F)",F,S); clip(currentpicture,(-1.5,-1)--(5,-1)--(5,3)--(-1.5,3)--cycle); [/asy]$ Assuming that $ADE$ is a triangle and applying the triangle inequality, we see that $AD > 20sqrt {7}$ . However, if $AD$ is strictly greater than $20sqrt {7}$ , then the circle with radius $10sqrt {21}$ and center $A$ does not touch $DC$ , which implies that $AC > 10sqrt {21}$ , a contradiction. As a result, A, D, and E are collinear. Therefore, $AD = 20sqrt {7}$ .

Thus, $ADC$ and $ACF$ are $30-60-90$ triangles. Hence $AF = 15sqrt {7}$ , and

$EF = EA + AF = 10sqrt {7} + 15sqrt {7} = 25sqrt {7}$ Finally, the answer is $25+7=boxed{032}$ .

No restrictions are set on the lengths of the bases, so for calculational simplicity let $angle CAF = 30^{circ}$ . Since $CAF$ is a $30-60-90$ triangle, $AF=frac{ACsqrt{3}}2=15sqrt{7}$ .

$EF=EA+AF=10sqrt{7}+15sqrt{7}=25sqrt{7}$ The answer is $25+7=boxed{032}$ . Note that while this is not rigorous, the above solution shows that $angle CAF = 30^{circ}$ is indeed the only possibility.

Extend $overline {AB}$ through $B$ , to meet $overline {DC}$ (extended through $C$ ) at $G$ . $ADG$ is an equilateral triangle because of the angle conditions on the base.

If $overline {GC} = x$ then $overline {CD} = 40sqrt{7}-x$ , because $overline{AD}$ and therefore $overline{GD}$ $= 40sqrt{7}$ .

By simple angle chasing, $CFD$ is a 30-60-90 triangle and thus $overline{FD} = frac{40sqrt{7}-x}{2}$ , and $overline{CF} = frac{40sqrt{21} - sqrt{3}x}{2}$

Similarly $CAF$ is a 30-60-90 triangle and thus $overline{CF} = frac{10sqrt{21}}{2} = 5sqrt{21}$ .

Equating and solving for $x$ , $x = 30sqrt{7}$ and thus $overline{FD} = frac{40sqrt{7}-x}{2} = 5sqrt{7}$ .

$overline{ED}-overline{FD} = overline{EF}$

$30sqrt{7} - 5sqrt{7} = 25sqrt{7}$ and $25 + 7 = boxed{032}$
Let $a_n$ and $b_n$ denote, respectively, the number of sequences of length $n$ ending in $A$ and $B$ . If a sequence ends in an $A$ , then it must have been formed by appending two $A$ s to the end of a string of length $n-2$ . If a sequence ends in a $B,$ it must have either been formed by appending one $B$ to a string of length $n-1$ ending in an $A$ , or by appending two $B$ s to a string of length $n-2$ ending in a $B$ . Thus, we have the recursions $begin{align*} a_n &= a_{n-2} + b_{n-2} b_n &= a_{n-1} + b_{n-2} end{align*}$ By counting, we find that $a_1 = 0, b_1 = 1, a_2 = 1, b_2 = 0$ . $[begin{array}{|r||r|r|||r||r|r|} hline n & a_n & b_n & n & a_n & b_n hline 1&0&1& 8&6&10 2&1&0& 9&11&11 3&1&2& 10&16&21 4&1&1& 11&22&27 5&3&3& 12&37&43 6&2&4& 13&49&64 7&6&5& 14&80&92 hline end{array}]$ Therefore, the number of such strings of length $14$ is $a_{14} + b_{14} = boxed{172}$ .Let $a_n$ and $b_n$ denote, respectively, the number of sequences of length $n$ ending in $A$ and $B$ .Additionally, let $t_n$ denote the total number of sequences of length $n$ . Then, $t_n=a_n+b_n$ , as the total amount of sequences of length $n$ consists of the sequences of length $n$ ending in $A$ and the sequences of length $n$ ending in $B$ . $begin{align*} a_n &= a_{n-2} + b_{n-2} b_n &= a_{n-1} + b_{n-2} end{align*}$ The recursion for $a_n$ tells us that $a_n=a_{n-2}+b_{n-2}$ . However, this is also the definition for $t_{n-2}$ . Therefore, $a_n=t_{n-2}$ .We also know from our recursion for $b_n$ that $b_n=a_{n-2}+b_{n-2}$ . Substituting for $a_n$ and $b_n$ into our recursion for $t_n$ gives us $t_n=t_{n-2}+a_{n-1}+b_{n-2}$ .Furthermore, note that since $a_n=t_{n-2}$ , $a_{n-1}=t_{n-3}$ . Furthermore, using our definition for $t_{n-2}$ , we can rewrite $b_{n-2}$ as $t_{n-2}-a_{n-2}$ . Substituting for $a_{n-1}$ and $b_{n-2}$ into our recursion for $t_n$ gives us $t_n=t_{n-2}+t_{n-3}+t_{n-2}-a_{n-2}$ .Finally, note that since $a_n=t_{n-2}$ , $a_{n-2}=t_{n-4}$ . Substituting for $a_{n-2}$ into our recursion for $t_n$ gives us $t_n=2t_{n-2}+t_{n-3}-t_{n-4}$ . We now have a recursion only in terms of $t$ .By counting, we find that $t_1=1$ , $t_2=1$ , $t_3=3$ , and $t_4=2$ . $[begin{array}{|r|r||r|r|} hline n & t_n & n & t_n hline 1&1&8&16 2&1&9&22 3&3&10&37 4&2&11&49 5&6&12&80 6&6&13&113 7&11&14&172 hline end{array}]$ Therefore, the number of such sequences of length 14 is $boxed{172}$ .
We replace "14" with " $2n$ ". We first note that we must have an even number of chunks of $B$ 's, because of parity issues. We then note that every chunk of $B$ 's except the last one must end in the sequence $BAA$ , since we need at least two $A$ 's to separate it from the next chunk of $B$ 's. The last chunk of $B$ 's must, of course, end with a $B$ . Thus our sequence must look like this : $[boxed{quad Atext{'s} quad} boxed{quad Btext{'s} quad} BAA boxed{quad Atext{'s} quad} cdots boxed{quad Btext{'s} quad}BAA boxed{quad Atext{'s} quad} boxed{quad Btext{'s} quad} B boxed{quad Atext{'s} quad} ,]$ where each box holds an even number of letters (possibly zero).

If we want a sequence with $2k$ chunks of $B$ 's, then we have $(2n - 6k + 2)$ letters with which to fill the boxes. Since each box must have an even number of letters, we may put the letters in the boxes in pairs. Then we have $(n - 3k + 1)$ pairs of letters to put into $4k + 1$ boxes. By a classic balls-and-bins argument, the number of ways to do this is $[binom{n + k + 1}{4k} .]$ It follows that the total number of desirable sequences is $[sum_k binom{n + k + 1}{4k} .]$ For $n = 7$ , this evaluates as $binom{8}{0} + binom{9}{4} + binom{10}{8} = 1 + 126 + 45 = boxed{172}$ .

There must be an even amount of runs of consecutive $B$ s due to parity. Thus, we can split this sequence into the following cases: $A$ , $BAAB$ , $AABAAB$ , $BAABAA$ , $AABAABAA$ , $BAABAABAAB$ , $AABAABAABAAB$ , $BAABAABAABAA$ , and $AABAABAABAABAA$ , in which the amount of letters in one run does not necessarily represent the amount of letters there can be.

For the first case and the last case, there is only one possible sequence of letters.

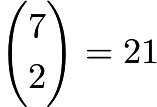For all other cases, we can insert two of the same letter at a time into a run that has the exact same letter. For example, for the second case, we can insert two $A$ s and make the sequence $BAAAAB$ . There are three "slots" in which we can insert two additional letters in, and we must insert five groups of new letters. By stars and bars, the number of ways for the second case is $binom{7}{2}=21$ .

Applying this logic to all of the other cases gives us $binom{7}{3}$ , $binom{7}{3}$ , $binom{7}{4}$ , $binom{8}{6}$ , $binom{8}{1}$ , and $binom{8}{1}$ . Adding 1+ $binom{7}{2}$ + $binom{7}{3}$ + $binom{7}{3}$ + $binom{7}{4}$ + $binom{8}{6}$ + $binom{8}{1}$ + $binom{8}{1}$ gives us the answer $boxed{172}$ .
Let $n$ be the number of car lengths that separates each car. Then their speed is at most $15n$ . Let a unit be the distance between the cars (front to front). Then the length of each unit is $4(n + 1)$ . To maximize, in a unit, the CAR comes first, THEN the empty space. So at time zero, the car is right at the eye.Hence, we count the number of units that pass the eye in an hour: $frac {15,000nfrac{text{meters}}{text{hour}}}{4(n + 1)frac{text{meters}}{text{unit}}} = frac {15,000n}{4(n + 1)}frac{text{units}}{text{hour}}$ . We wish to maximize this.Observe that as $n$ gets larger, the $+ 1$ gets less and less significant, so we take the limit as $n$ approaches infinity $lim_{nrightarrow infty}frac {15,000n}{4(n + 1)} = lim_{nrightarrow infty}frac {15,000n}{4n} = frac {15,000}{4} = 3750$ Now, as the speeds are clearly finite, we can never actually reach $3750$ full UNITs. However, we only need to find the number of CARS. We can increase their speed so that the camera stops (one hour goes by) after the car part of the $3750$ th unit has passed, but not all of the space behind it. Hence, $3750$ cars is possible, and the answer is $boxed {375}$ .Disclaimer: This is for the people who may not understand calculus, and is also how I did it. First, we assume several things. First, we assume the speeds must be multiples of 15 to maximize cars, because any less will be a waste. Second, we assume each car goes at the same speed. Third, we start with one car in front of the photoelectric eye. We first set the speed of the cars as $15k$ . Then, the distance between them is $frac{4}{1000} times k~km$ . Therefore, it takes the car closest to the eye not on the eye $frac{frac{k}{250}}{15k}$ hours to get to the eye. There is one hour, so the amount of cars that can pass is $frac{1}{frac{frac{k}{250}}{15k}}$ , or $3750$ cars. When divided by ten, you get the quotient of $boxed{375}$
$begin{align*} p(0,0) &= a_0 = 0 p(1,0) &= a_0 + a_1 + a_3 + a_6 = a_1 + a_3 + a_6 = 0 p(-1,0) &= -a_1 + a_3 - a_6 = 0end{align*}$ Adding the above two equations gives $a_3 = 0$ , and so we can deduce that $a_6 = -a_1$ .Similarly, plugging in $(0,1)$ and $(0,-1)$ gives $a_5 = 0$ and $a_9 = -a_2$ . Now, $begin{align*}p(1,1) &= a_0 + a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + a_9 &= 0 + a_1 + a_2 + 0 + a_4 + 0 - a_1 + a_7 + a_8 - a_2 = a_4 + a_7 + a_8 = 0 p(1,-1) &= a_0 + a_1 - a_2 + 0 - a_4 + 0 - a_1 - a_7 + a_8 + a_2 &= -a_4 - a_7 + a_8 = 0end{align*}$ Therefore $a_8 = 0$ and $a_7 = -a_4$ . Finally, $p(2,2) = 0 + 2a_1 + 2a_2 + 0 + 4a_4 + 0 - 8a_1 - 8a_4 +0 - 8a_2 = -6 a_1 - 6 a_2 - 4 a_4 = 0$ So $3a_1 + 3a_2 + 2a_4 = 0$ .Now $p(x,y) = 0 + x a_1 + y a_2 + 0 + xy a_4 + 0 - x^3 a_1 - x^2 y a_4 + 0 - y^3 a_2$ $= x(1-x)(1+x) a_1 + y(1-y)(1+y) a_2 + xy (1-x) a_4$ .In order for the above to be zero, we must have $x(1-x)(1+x) = y(1-y)(1+y)$ and $x(1-x)(1+x) = 1.5 xy (1-x).$ Canceling terms on the second equation gives us $1+x = 1.5 y Longrightarrow x = 1.5 y - 1$ . Plugging that into the first equation and solving yields $x = 5/19, y = 16/19$ , and $5+16+19 = boxed{040}$ .Consider the cross section of $z = p(x, y)$ on the plane $z = 0$ . We realize that we could construct the lines/curves in the cross section such that their equations multiply to match the form of $p(x, y)$ and they go over the eight given points. A simple way to do this would be to use the equations $x = 0$ , $x = 1$ , and $y = frac{2}{3}x + frac{2}{3}$ , giving us
$p_1(x, y) = xleft(x - 1right)left( frac{2}{3}x - y + frac{2}{3}right) = frac{2}{3}x + xy + frac{2}{3}x^3-x^2y$ .

Another way to do this would to use the line $y = x$ and the ellipse, $x^2 + xy + y^2 = 1$ . This would give

$p_2(x, y) = left(x - yright)left(x^2 + xy + y^2 - 1right) = -x + y + x^3 - y^3$ .

At this point, we see that $p_1$ and $p_2$ both must have $left(frac{a}{c}, frac{b}{c}right)$ as a zero. A quick graph of the 4 lines and the ellipse used to create $p_1$ and $p_2$ gives nine intersection points. Eight of them are the given ones, and the ninth is $left(frac{5}{9}, frac{16}{9}right)$ . The last intersection point can be found by finding the intersection points of $y = frac{2}{3}x + frac{2}{3}$ and $x^2 + xy + y^2 = 1$ . Finally, just add the values of $a$ , $b$ , and $c$ to get $5 + 16 + 19 = boxed{040}$
$[asy] size(250); defaultpen(0.70 + fontsize(10)); import olympiad; pair O = (0,0), B = O - (9,0), A= O + (9,0), C=A+(18,0), T = 9 * expi(-1.2309594), P = foot(A,C,T); draw(Circle(O,9)); draw(B--C--T--O); draw(A--P); dot(A); dot(B); dot(C); dot(O); dot(T); dot(P); draw(rightanglemark(O,T,C,30)); draw(rightanglemark(A,P,C,30)); draw(anglemark(B,A,P,35)); draw(B--P, blue); label("(A)",A,NW); label("(B)",B,NW); label("(C)",C,NW); label("(O)",O,NW); label("(P)",P,SE); label("(T)",T,SE); label("(9)",(O+A)/2,N); label("(9)",(O+B)/2,N); label("(x-9)",(C+A)/2,N); [/asy]$ Let $x = OC$ . Since $OT, AP perp TC$ , it follows easily that $triangle APC sim triangle OTC$ . Thus $frac{AP}{OT} = frac{CA}{CO} Longrightarrow AP = frac{9(x-9)}{x}$ . By the Law of Cosines on $triangle BAP$ , $begin{align*}BP^2 = AB^2 + AP^2 - 2 cdot AB cdot AP cdot cos angle BAP end{align*}$ where $cos angle BAP = cos (180 - angle TOA) = - frac{OT}{OC} = - frac{9}{x}$ , so: $begin{align*}BP^2 &= 18^2 + frac{9^2(x-9)^2}{x^2} + 2(18) cdot frac{9(x-9)}{x} cdot frac 9x = 405 + 729left(frac{2x - 27}{x^2}right)end{align*}$ Let $m = frac{2x-27}{x^2} Longrightarrow mx^2 - 2x + 27 = 0$ ; this is a quadratic, and its discriminant must be nonnegative: $(-2)^2 - 4(m)(27) ge 0 Longleftrightarrow m le frac{1}{27}$ . Thus, $[BP^2 le 405 + 729 cdot frac{1}{27} = boxed{432}]$ Equality holds when $x = 27$ .Proceed as follows for Solution 1.Once you approach the function $m=(2x-27)/x^2$ , find the maximum value by setting $dm/dx=0$ .Simplifying $m$ to take the derivative, we have $2/x-27/x^2$ , so $dm/dx=-2/x^2+54/x^3$ . Setting $dm/dx=0$ , we have $2/x^2=54/x^3$ .Solving, we obtain $x=27$ as the critical value. Hence, $m$ has the maximum value of $(2*27-27)/27^2=1/27$ . Since $BP^2=405+729m$ , the maximum value of $overline {BP}$ occurs at $m=1/27$ , so $BP^2$ has a maximum value of $405+729/27=fbox{432}$ .Note: Please edit this solution if it feels inadequate. $[asy] unitsize(3mm); pair B=(0,13.5), C=(23.383,0); pair O=(7.794, 9), P=(2*7.794,0); pair T=(7.794,0), Q=(0,0); pair A=(2*7.794,4.5); draw(Q--B--C--Q); draw(O--T); draw(A--P); draw(Circle(O,9)); dot(A);dot(B);dot(C);dot(T);dot(P);dot(O);dot(Q); label("(B)",B,NW); label("(A)",A,NE); label("(omega)",O,N); label("(P)",P,S); label("(T)",T,S); label("(Q)",Q,S); label("(C)",C,E); label("(theta)",C + (-1.7,-0.2), NW); label("(9)", (B+O)/2, N); label("(9)", (O+A)/2, N); label("(9)", (O+T)/2,W); [/asy]$ From the diagram, we see that $BQ = omega T + Bomegasintheta = 9 + 9sintheta = 9(1 + sintheta)$ , and that $QP = BAcostheta = 18costheta$ . $begin{align*}BP^2 &= BQ^2 + QP^2 = 9^2(1 + sintheta)^2 + 18^2cos^2theta &= 9^2[1 + 2sintheta + sin^2theta + 4(1 - sin^2theta)] BP^2 &= 9^2[5 + 2sintheta - 3sin^2theta]end{align*}$
This is a quadratic equation, maximized when $sintheta = frac { - 2}{ - 6} = frac {1}{3}$ . Thus, $m^2 = 9^2[5 + frac {2}{3} - frac {1}{3}] = boxed{432}$ .

(Diagram credit goes to Solution 2)

We let $AC=x$ . From similar triangles, we have that $PC=frac{xsqrt{x^2+18x}}{x+9}$ . Similarly, $TP=QT=frac{9sqrt{x^2+18x}}{x+9}$ . Using the Pythagorean Theorem, $BQ=sqrt{(x+18)^2-(frac{(x+18)sqrt{x^2+18x}}{x+9})^2}$ . Using the Pythagorean Theorem once again, $BP=sqrt{(x+18)^2-(frac{(x+18)sqrt{x^2+18x}}{x+9})^2+(frac{18sqrt{x^2+18x}}{x+9})^2}$ . After a large bashful simplification, $BP=sqrt{405+frac{1458x-6561}{x^2+18x+81}}$ . The fraction is equivalent to $729frac{2x-9}{(x+9)^2}$ . Taking the derivative of the fraction and solving for x, we get that $x=18$ . Plugging $x=18$ back into the expression for $BP$ yields $sqrt{432}$ , so the answer is $(sqrt{432})^2=boxed{432}$ .
In the original picture, let $P$ be the corner, and $M$ and $N$ be the two points whose distance is $sqrt{17}$ from $P$ . Also, let $R$ be the point where the two cuts intersect.Using $triangle{MNP}$ (a 45-45-90 triangle), $MN=MPsqrt{2}quadLongrightarrowquad MN=sqrt{34}$ . $triangle{MNR}$ is equilateral, so $MR = NR = sqrt{34}$ . (Alternatively, we could find this by the Law of Sines.)The length of the perpendicular from $P$ to $MN$ in $triangle{MNP}$ is $frac{sqrt{17}}{sqrt{2}}$ , and the length of the perpendicular from $R$ to $MN$ in $triangle{MNR}$ is $frac{sqrt{51}}{sqrt{2}}$ . Adding those two lengths, $PR=frac{sqrt{17}+sqrt{51}}{sqrt{2}}$ . (Alternatively, we could have used that $sin 75^{circ} = sin (30+45) = frac{sqrt{6}+sqrt{2}}{4}$ .)Drop a perpendicular from $R$ to the side of the square containing $M$ and let the intersection be $G$ . $begin{align*}PG&=frac{PR}{sqrt{2}}=frac{sqrt{17}+sqrt{51}}{2} MG=PG-PM&=frac{sqrt{17}+sqrt{51}}{2}-sqrt{17}=frac{sqrt{51}-sqrt{17}}{2}end{align*}$ $[asy]import cse5; size(200); pathpen=black; real s=sqrt(17), r=(sqrt(51)+s)/(sqrt(2)); pair P=(0,0), N=(0,sqrt(17)), M=(sqrt(17),0), R=r*dir(45), G=((sqrt(51)+sqrt(17))/2,0); D(2*N--P--2*M); D(N--R--M); D(P--R); D((R.x,2*N.y)--R--(2*M.x,R.y)); MP("30^circ",R-(0.25,1),SW); MP("30^circ",R-(1,0.5),SW); MP("sqrt{17}",N/2,W); MP("sqrt{17}",M/2,S); D(N--M,dashed); D(G--R,dashed); MP("P",P,SW); MP("N",N,SW); MP("M",M,SW); MP("R",R,NE); MP("G",G,SW); [/asy]$ Let $ABCD$ be the smaller square base of the tray and let $A'B'C'D'$ be the larger square, such that $AA'$ , etc, are edges. Let $F$ be the foot of the perpendicular from $A$ to plane $A'B'C'D'$ .We know $AA'=MR=sqrt{34}$ and $A'F=MGsqrt{2}=frac{sqrt{51}-sqrt{17}}{sqrt{2}}$ . Now, use the Pythagorean Theorem on triangle $AFA'$ to find $AF$ : $begin{align*}left(frac{sqrt{51}-sqrt{17}}{sqrt{2}}right)^2+AF^2&=left(sqrt{34}right)^2 frac{51-34sqrt{3}+17}{2}+AF^2&=34AF&=sqrt{34-frac{68-34sqrt{3}}{2}}AF&=sqrt{frac{34sqrt{3}}{2}}AF&=sqrt[4]{867}end{align*}$
The answer is $867 + 4 = boxed{871}$ .

In the final pyramid, let $ABCD$ be the smaller square and let $A'B'C'D'$ be the larger square such that $AA'$ , etc. are edges.

It is obvious from the diagram that $angle A'AB = angle A'AD = 105^circ$ .

Let $AB$ and $AD$ be the positive $x$ and $y$ axes in a 3-d coordinate system such that $A'$ has a positive $z$ coordinate. Let $alpha$ be the angle made with the positive $x$ axis. Define $beta$ and $gamma$ analogously.

It is easy to see that if $P: = (x,y,z)$ , then $x = AA'cdot cosalpha$ . Furthermore, this means that $frac {x^2}{AA'^2} + frac {y^2}{AA'^2} + frac {z^2}{AA'^2} = cos^2alpha + cos^2beta + cos^2gamma = 1$ .

We have that $alpha = beta = 105^circ$ , so $cos^2 105^circ + cos^2105^circ + cos^2gamma = 1implies cosgamma = sqrt [4]{frac {3}{4}}$ .

It is easy to see from the Law of Sines that $frac {AA'}{sin 45^circ} = frac {sqrt {17}}{sin 30^circ}implies AA' = sqrt {34}$ .

Now, $z = AA'cdot cosgamma = sqrt [4]{34^2cdot frac {3}{4}} = sqrt [4]{867}$ .

It follows that the answer is $867 + 4 = boxed{871}$ .