Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2008 AMC12B 真题及答案详细解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月6日上午10:42

2008 AMC 12 B 真题

答案详细解析请参考文末

Problem 1

A basketball player made $5$ baskets during a game. Each basket was worth either $2$ or $3$ points. How many different numbers could represent the total points scored by the player?

$textbf{(A)} 2 qquad textbf{(B)} 3 qquad textbf{(C)} 4 qquad textbf{(D)} 5 qquad textbf{(E)} 6$

Problem 2

A $4times 4$ block of calendar dates is shown. The order of the numbers in the second row is to be reversed. Then the order of the numbers in the fourth row is to be reversed. Finally, the numbers on each diagonal are to be added. What will be the positive difference between the two diagonal sums?

$begin{tabular}[t]{|c|c|c|c|} multicolumn{4}{c}{}hline 1&2&3&4hline 8&9&10&11hline 15&16&17&18hline 22&23&24&25hline end{tabular}$

$textbf{(A)} 2 qquad textbf{(B)} 4 qquad textbf{(C)} 6 qquad textbf{(D)} 8 qquad textbf{(E)} 10$

Problem 3

A semipro baseball league has teams with $21$ players each. League rules state that a player must be paid at least $15,000$ dollars, and that the total of all players' salaries for each team cannot exceed $700,000$ dollars. What is the maximum possible salary, in dollars, for a single player?

$textbf{(A)} 270,000 qquad textbf{(B)} 385,000 qquad textbf{(C)} 400,000 qquad textbf{(D)} 430,000 qquad textbf{(E)} 700,000$

Problem 4

On circle $O$ , points $C$ and $D$ are on the same side of diameter $overline{AB}$ , $angle AOC = 30^circ$ , and $angle DOB = 45^circ$ . What is the ratio of the area of the smaller sector $COD$ to the area of the circle?

$[asy] unitsize(6mm); defaultpen(linewidth(0.7)+fontsize(8pt)); pair C = 3*dir (30); pair D = 3*dir (135); pair A = 3*dir (0); pair B = 3*dir(180); pair O = (0,0); draw (Circle ((0, 0), 3)); label ("(C)", C, NE); label ("(D)", D, NW); label ("(B)", B, W); label ("(A)", A, E); label ("(O)", O, S); label ("(45^circ)", (-0.3,0.1), WNW); label ("(30^circ)", (0.5,0.1), ENE); draw (A--B); draw (O--D); draw (O--C); [/asy]$

$textbf{(A)} frac {2}{9} qquad textbf{(B)} frac {1}{4} qquad textbf{(C)} frac {5}{18} qquad textbf{(D)} frac {7}{24} qquad textbf{(E)} frac {3}{10}$

Problem 5

A class collects $50$ dollars to buy flowers for a classmate who is in the hospital. Roses cost $3$ dollars each, and carnations cost $2$ dollars each. No other flowers are to be used. How many different bouquets could be purchased for exactly $50$ dollars?

$textbf{(A)} 1 qquad textbf{(B)} 7 qquad textbf{(C)} 9 qquad textbf{(D)} 16 qquad textbf{(E)} 17$

Problem 6

Postman Pete has a pedometer to count his steps. The pedometer records up to $99999$ steps, then flips over to $00000$ on the next step. Pete plans to determine his mileage for a year. On January $1$ Pete sets the pedometer to $00000$ . During the year, the pedometer flips from $99999$ to $00000$ forty-four times. On December $31$ the pedometer reads $50000$ . Pete takes $1800$ steps per mile. Which of the following is closest to the number of miles Pete walked during the year?

$textbf{(A)} 2500 qquad textbf{(B)} 3000 qquad textbf{(C)} 3500 qquad textbf{(D)} 4000 qquad textbf{(E)} 4500$

Problem 7

For real numbers $a$ and $b$ , define $a$ $ $b = (a - b)^2$ . What is $(x - y)^2$ $ $(y - x)^2$ ?

$textbf{(A)} 0 qquad textbf{(B)} x^2 + y^2 qquad textbf{(C)} 2x^2 qquad textbf{(D)} 2y^2 qquad textbf{(E)} 4xy$

Problem 8

Points $B$ and $C$ lie on $overline{AD}$ . The length of $overline{AB}$ is $4$ times the length of $overline{BD}$ , and the length of $overline{AC}$ is $9$ times the length of $overline{CD}$ . The length of $overline{BC}$ is what fraction of the length of $overline{AD}$ ?

$textbf{(A)} frac {1}{36} qquad textbf{(B)} frac {1}{13} qquad textbf{(C)} frac {1}{10} qquad textbf{(D)} frac {5}{36} qquad textbf{(E)} frac {1}{5}$

Problem 9

Points $A$ and $B$ are on a circle of radius $5$ and $AB = 6$ . Point $C$ is the midpoint of the minor arc $AB$ . What is the length of the line segment $AC$ ?

$textbf{(A)} sqrt {10} qquad textbf{(B)} frac {7}{2} qquad textbf{(C)} sqrt {14} qquad textbf{(D)} sqrt {15} qquad textbf{(E)} 4$

Problem 10

Bricklayer Brenda would take $9$ hours to build a chimney alone, and bricklayer Brandon would take $10$ hours to build it alone. When they work together they talk a lot, and their combined output is decreased by $10$ bricks per hour. Working together, they build the chimney in $5$ hours. How many bricks are in the chimney?

$textbf{(A)} 500 qquad textbf{(B)} 900 qquad textbf{(C)} 950 qquad textbf{(D)} 1000 qquad textbf{(E)} 1900$

Problem 11

A cone-shaped mountain has its base on the ocean floor and has a height of 8000 feet. The top $frac{1}{8}$ of the volume of the mountain is above water. What is the depth of the ocean at the base of the mountain in feet?

$textbf{(A)} 4000 qquad textbf{(B)} 2000(4-sqrt{2}) qquad textbf{(C)} 6000 qquad textbf{(D)} 6400 qquad textbf{(E)} 7000$

Problem 12

For each positive integer $n$ , the mean of the first $n$ terms of a sequence is $n$ . What is the $2008$ th term of the sequence?

$textbf{(A)} 2008 qquad textbf{(B)} 4015 qquad textbf{(C)} 4016 qquad textbf{(D)} 4030056 qquad textbf{(E)} 4032064$

Problem 13

Vertex $E$ of equilateral triangle $triangle ABE$ is in the interior of unit square $ABCD$ . Let $R$ be the region consisting of all points inside $ABCD$ and outside $triangle ABE$ whose distance from $overline{AD}$ is between $frac{1}{3}$ and $frac{2}{3}$ . What is the area of $R$ ?

$textbf{(A)} frac{12-5sqrt{3}}{72} qquad textbf{(B)} frac{12-5sqrt{3}}{36} qquad textbf{(C)} frac{sqrt{3}}{18} qquad textbf{(D)} frac{3-sqrt{3}}{9} qquad textbf{(E)} frac{sqrt{3}}{12}$

Problem 14

A circle has a radius of $log_{10}{(a^2)}$ and a circumference of $log_{10}{(b^4)}$ . What is $log_{a}{b}$ ?

$textbf{(A)} frac{1}{4pi} qquad textbf{(B)} frac{1}{pi} qquad textbf{(C)} pi qquad textbf{(D)} 2pi qquad textbf{(E)} 10^{2pi}$

Problem 15

On each side of a unit square, an equilateral triangle of side length 1 is constructed. On each new side of each equilateral triangle, another equilateral triangle of side length 1 is constructed. The interiors of the square and the 12 triangles have no points in common. Let $R$ be the region formed by the union of the square and all the triangles, and $S$ be the smallest convex polygon that contains $R$ . What is the area of the region that is inside $S$ but outside $R$ ?

$textbf{(A)} ; frac {1}{4} qquad textbf{(B)} ; frac {sqrt {2}}{4} qquad textbf{(C)} ; 1 qquad textbf{(D)} ; sqrt {3} qquad textbf{(E)} ; 2 sqrt {3}$

Problem 16

A rectangular floor measures $a$ by $b$ feet, where $a$ and $b$ are positive integers with $b > a$ . An artist paints a rectangle on the floor with the sides of the rectangle parallel to the sides of the floor. The unpainted part of the floor forms a border of width $1$ foot around the painted rectangle and occupies half of the area of the entire floor. How many possibilities are there for the ordered pair $(a,b)$ ?

$textbf{(A)} 1qquadtextbf{(B)} 2qquadtextbf{(C)} 3qquadtextbf{(D)} 4qquadtextbf{(E)} 5$

Problem 17

Let $A$ , $B$ and $C$ be three distinct points on the graph of $y=x^2$ such that line $AB$ is parallel to the $x$ -axis and $triangle ABC$ is a right triangle with area $2008$ . What is the sum of the digits of the $y$ -coordinate of $C$ ?

$textbf{(A)} 16qquadtextbf{(B)} 17qquadtextbf{(C)} 18qquadtextbf{(D)} 19qquadtextbf{(E)} 20$

Problem 18

A pyramid has a square base $ABCD$ and vertex $E$ . The area of square $ABCD$ is $196$ , and the areas of $triangle ABE$ and $triangle CDE$ are $105$ and $91$ , respectively. What is the volume of the pyramid?

$textbf{(A)} 392 qquad textbf{(B)} 196sqrt {6} qquad textbf{(C)} 392sqrt {2} qquad textbf{(D)} 392sqrt {3} qquad textbf{(E)} 784$

Problem 19

A function $f$ is defined by $f(z) = (4 + i) z^2 + alpha z + gamma$ for all complex numbers $z$ , where $alpha$ and $gamma$ are complex numbers and $i^2 = - 1$ . Suppose that $f(1)$ and $f(i)$ are both real. What is the smallest possible value of $| alpha | + |gamma |$ ?

$textbf{(A)} ; 1 qquad textbf{(B)} ; sqrt {2} qquad textbf{(C)} ; 2 qquad textbf{(D)} ; 2 sqrt {2} qquad textbf{(E)} ; 4 qquad$

Problem 20

Michael walks at the rate of $5$ feet per second on a long straight path. Trash pails are located every $200$ feet along the path. A garbage truck travels at $10$ feet per second in the same direction as Michael and stops for $30$ seconds at each pail. As Michael passes a pail, he notices the truck ahead of him just leaving the next pail. How many times will Michael and the truck meet?

$textbf{(A)} 4qquad textbf{(B)} 5qquad textbf{(C)} 6qquad textbf{(D)} 7qquad textbf{(E)} 8$

Problem 21

Two circles of radius 1 are to be constructed as follows. The center of circle $A$ is chosen uniformly and at random from the line segment joining $(0,0)$ and $(2,0)$ . The center of circle $B$ is chosen uniformly and at random, and independently of the first choice, from the line segment joining $(0,1)$ to $(2,1)$ . What is the probability that circles $A$ and $B$ intersect?

$textbf{(A)} ; frac {2 + sqrt {2}}{4} qquad textbf{(B)} ; frac {3sqrt {3} + 2}{8} qquad textbf{(C)} ; frac {2 sqrt {2} - 1}{2} qquad textbf{(D)} ; frac {2 + sqrt {3}}{4} qquad textbf{(E)} ; frac {4 sqrt {3} - 3}{4}$

Problem 22

A parking lot has 16 spaces in a row. Twelve cars arrive, each of which requires one parking space, and their drivers chose spaces at random from among the available spaces. Auntie Em then arrives in her SUV, which requires 2 adjacent spaces. What is the probability that she is able to park?

$textbf{(A)} ; frac {11}{20} qquad textbf{(B)} ; frac {4}{7} qquad textbf{(C)} ; frac {81}{140} qquad textbf{(D)} ; frac {3}{5} qquad textbf{(E)} ; frac {17}{28}$

Problem 23

The sum of the base- $10$ logarithms of the divisors of $10^n$ is $792$ . What is $n$ ?

$textbf{(A)} 11qquad textbf{(B)} 12qquad textbf{(C)} 13qquad textbf{(D)} 14qquad textbf{(E)} 15$

Problem 24

Let $A_0 = (0,0)$ . Distinct points $A_1,A_2,ldots$ lie on the $x$ -axis, and distinct points $B_1,B_2,ldots$ lie on the graph of $y = sqrt {x}$ . For every positive integer $n$ , $A_{n - 1}B_nA_n$ is an equilateral triangle. What is the least $n$ for which the length $A_0A_nge100$ ?

$textbf{(A)} 13qquad textbf{(B)} 15qquad textbf{(C)} 17qquad textbf{(D)} 19qquad textbf{(E)} 21$

Problem 25

Let $ABCD$ be a trapezoid with $AB||CD$ , $AB = 11$ , $BC = 5$ , $CD = 19$ , and $DA = 7$ . Bisectors of $angle A$ and $angle D$ meet at $P$ , and bisectors of $angle B$ and $angle C$ meet at $Q$ . What is the area of hexagon $ABQCDP$ ?

$textbf{(A)} 28sqrt {3}qquad textbf{(B)} 30sqrt {3}qquad textbf{(C)} 32sqrt {3}qquad textbf{(D)} 35sqrt {3}qquad textbf{(E)} 36sqrt {3}$

2008 AMC12 B 真题答案详细解析

Solution 1
If the basketball player makes $x$ three-point shots and $5-x$ two-point shots, he scores $3x+2(5-x)=10+x$ points. Clearly every value of $x$ yields a different number of total points. Since he can make any number of three-point shots between $0$ and $5$ inclusive, the number of different point totals is $6 Rightarrow E$ Solution 2
Stars and bars can also be utilized to solve this problem. Since we need to decide what number of 2's and 3's are scored, and there are a total of 5 shots. It can be written like such: _ _ _ | _ _. Solving this, we get $6 Rightarrow E$
After reversing the numbers on the second and fourth rows, the block will look like this:
We want to find the maximum any player could make, so assume that everyone else makes the minimum possible and that the combined salaries total the maximum of $700,000$ $700,000 = 20 * 15,000 + x$ $x = 400,000$ The maximum any player could make is $400,000$ dollars $Rightarrow C$
$angle COD = angle AOB - angle AOC - angle BOD = 180^circ - 30^circ - 45^circ = 105^circ$ .Since a circle has $360^circ$ , the desired ratio is $frac{105^circ}{360^circ}=frac{7}{24} Rightarrow D$ .
The class could send $25$ carnations and no roses, $22$ carnations and $2$ roses, $19$ carnations and $4$ roses, and so on, down to $1$ carnation and $16$ roses. There are 9 total possibilities (from 0 to 16 roses, incrementing by 2 at each step), $Rightarrow boxed{C}$
Every time the pedometer flips, Pete has walked $100,000$ steps. Therefore, Pete has walked a total of $100,000 * 44 + 50,000 = 4,450,000$ steps, which is $4,450,000/1,800 = 2472.2$ miles, which is closest to answer choice $boxed{A}$ .
$left[ (x-y)^2 - (y-x)^2 right]^2$ $left[ (x-y)^2 - (x-y)^2 right]^2$ $[0]^2$ $0 Rightarrow textbf{(A)}$
Since $overline{AB}=4overline{BD}$ and $overline{AB}+overline{BD}=overline{AD}$ , $overline{AB}=frac{4}{5}overline{AD}$ .Since $overline{AC}=9overline{CD}$ and $overline{AC}+overline{CD}=overline{AD}$ , $overline{AC}=frac{9}{10}overline{AD}$ .Thus, $overline{BC}=overline{AC}-overline{AB}=left(frac{9}{10}-frac{4}{5}right)overline{AD} = frac {1}{10}overline{AD} Rightarrow C$ .
Solution 1

Let $alpha$ be the angle that subtends the arc $AB$ . By the law of cosines, $6^2=5^2+5^2-2cdot 5cdot 5cos(alpha)$ implies $cos(alpha) = 7/25$ .

The half-angle formula says that $2008 AMC12B 真题及答案详细解析$ . The law of cosines tells us $AC = sqrt{5^2+5^2-2cdot 5cdot 5cdot frac{4}{5}} = sqrt{50-50frac{4}{5}} = sqrt{10}$ , which is answer choice $boxed{text{A}}$ .

Solution 2

$[asy] defaultpen(fontsize(8)); pair A=(-3,4), B=(3,4), C=(0,5), D=(0,4), O=(0,0); D(Circle(O,5)); D(O--B--A--O--C);D(A--C--B); label("$A$",A,(-1,1));label("$O$",O,(0,-1));label("$B$",B,(1,1));label("$C$",C,(0,1));label("$D$",D,(-1,-1)); [/asy]$

Figure 1

Define $D$ as the midpoint of line segment $overline{AB}$ , and $O$ the center of the circle. Then $O$ , $C$ , and $D$ are collinear, and since $D$ is the midpoint of $AB$ , $mangle ODA=90deg$ and so $OD=sqrt{5^2-3^2}=4$ . Since $OD=4$ , $CD=5-4=1$ , and so $AC=sqrt{3^2+1^2}=sqrt{10} rightarrow boxed{text{A}}$ .
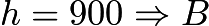Let $h$ be the number of bricks in the chimney.Without talking, Brenda and Brandon lay $frac{h}{9}$ and $frac{h}{10}$ bricks per hour respectively, so together they lay $frac{h}{9}+frac{h}{10}-10$ per hour together.Since they finish the chimney in $5$ hours, $h=5left( frac{h}{9}+frac{h}{10}-10 right)$ . Thus, $h=900 Rightarrow B$ .
In a cone, radius and height each vary inversely with increasing height (i.e. the radius of the cone formed by cutting off the mountain at $4,000$ feet is half that of the original mountain). Therefore, volume varies as the inverse cube of increasing height (expressed as a percentage of the total height of cone): $V_Itimes text{Height}^3 = V_N$ Plugging in our given condition, $frac{1}{8} = text{Height}^3 Rightarrow text{Height} = frac{1}{2}$ . $8000cdotfrac{1}{2}=4000 Rightarrow boxed{textbf{A}}$ .
For each positive integer $n$ , the mean of the first $n$ terms of a sequence is $n$ . What is the $2008$ th term of the sequence? $textbf{(A)} 2008 qquad textbf{(B)} 4015 qquad textbf{(C)} 4016 qquad textbf{(D)} 4030056 qquad textbf{(E)} 4032064$

Solution

Letting $S_n$ be the nth partial sum of the sequence:

$frac{S_n}{n} = n$

$S_n = n^2$

The only possible sequence with this result is the sequence of odd integers.

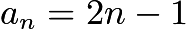
$a_n = 2n - 1$

$a_{2008} = 2(2008) - 1 = 4015 Rightarrow textbf{(B)}$

Alternate Solution

Letting the sum of the sequence equal $a_1+a_2+cdots+a_n$ yields the following two equations:

$frac{a_1+a_2+cdots+a_{2008}}{2008}=2008$ and

$frac{a_1+a_2+cdots+a_{2007}}{2007}=2007$ .

Therefore:

$a_1+a_2+cdots+a_{2008}=2008^2$ and $a_1+a_2+cdots+a_{2007}=2007^2$

Hence, by substitution, $a_{2008}=2008^2-2007^2=(2008+2007)(2008-2007)=4015(1)=4015impliesboxed{textbf{B}}$
The region is the shaded area: $[asy] pair A,B,C,D,E; A=(0,1); B=(1,1); C=(1,0); D=(0,0); E=(1/2,1-sqrt(3)/2); draw(A--B--C--D--cycle); label("A",A,NW); dot(A); label("B",B,NE); dot(B); label("C",C,SE); dot(C); label("D",D,SW); dot(D); draw(A--E--B--cycle); label("E",E,S); dot(E); draw((1/3,0)--(1/3,1)); draw((2/3,0)--(2/3,1)); fill((1/3,0)--(1/3,1-sqrt(3)/3)--E--(2/3,1-sqrt(3)/3)--(2/3,0)--cycle,Black);[/asy]$ We can find the area of the shaded region by subtracting the pentagon from the middle third of the square. The area of the middle third of the square is $left(frac13right)(1)=frac13$ . The pentagon can be split into a rectangle and an equilateral triangle.The base of the equilateral triangle is $frac13$ and the height is $left(frac13right)left(frac12right)(sqrt{3})=frac{sqrt{3}}{6}$ . Thus, the area is $left(frac{sqrt3}{6}right)left(frac13right)left(frac12right)=frac{sqrt3}{36}$ .The base of the rectangle is $frac13$ and the height is the height of the equilateral triangle minus the height of the smaller equilateral triangle. This is: $frac{sqrt3}{2}-frac{sqrt3}{6}=frac{sqrt3}{3}$ Therefore, the area of the shaded region is $frac13-frac{sqrt3}{9}-frac{sqrt3}{36}=boxed{text{(B) }frac{12-5sqrt3}{36}}.$
Let $C$ be the circumference of the circle, and let $r$ be the radius of the circle.Using log properties, $C=log_{10}{(b^4)}=4log_{10}{(b)}$ and $r=log_{10}{(a^2)}=2log_{10}{(a)}$ .Since $C=2pi r$ , $4log_{10}{(b)}=2picdot2log_{10}{(a)} Rightarrow log_{a}{b} = frac{log_{10}{(b)}}{log_{10}{(a)}}=pi Rightarrow C$ .
$[asy] real a = 1/2, b = sqrt(3)/2; draw((0,0)--(1,0)--(1,1)--(0,1)--cycle); draw((0,0)--(a,-b)--(1,0)--(1+b,a)--(1,1)--(a,1+b)--(0,1)--(-b,a)--(0,0)); draw((0,0)--(-1+a,-b)--(1+a,-b)--(1,0)--(1+b,-1+a)--(1+b,1+a)--(1,1)--(1+a,1+b)--(-1+a,1+b)--(0,1)--(-b,1+a)--(-b,-1+a)--(0,0)); filldraw((1+a,-b)--(1,0)--(1+b,-1+a)--cycle,gray(0.9)); filldraw((1+b,1+a)--(1,1)--(1+a,1+b)--cycle,gray(0.9)); filldraw((-1+a,1+b)--(0,1)--(-b,1+a)--cycle,gray(0.9)); filldraw((-b,-1+a)--(0,0)--(-1+a,-b)--cycle,gray(0.9)); [/asy]$
The equilateral triangles form trapezoids with side lengths $1, 1, 1, 2$ (half a unit hexagon) on each face of the unit square. The four triangles "in between" these trapezoids are isosceles triangles with two side lengths $1$ and an angle of $30^{circ}$ in between them, so the total area of these triangles (which is the area of $S - R$ ) is, $4 left( frac {1}{2} sin 30^{circ} right) = 1$ which makes the answer $boxed{C}$ .
$A_{outer}=ab$ $A_{inner}=(a-2)(b-2)$ $A_{outer}=2A_{inner}$ $ab=2(a-2)(b-2)=2ab-4a-4b+8$ $0=ab-4a-4b+8$ By Simon's Favorite Factoring Trick: $8=ab-4a-4b+16=(a-4)(b-4)$ Since $8=1times8$ and $8=2times4$ are the only positive factorings of $8$ . $(a,b)=(5,12)$ or $(a,b)=(6,8)$ yielding $2Rightarrow textbf{(B)}$ solutions. Notice that because $b>a$ , the reversed pairs are invalid.
Supposing $angle A=90^circ$ , $AC$ is perpendicular to $AB$ and, it follows, to the $x$ -axis, making $AC$ a segment of the line $x=a$ . But that would mean that the coordinates of $C$ are $(a, a^2)$ , contradicting the given that points $A$ and $C$ are distinct. So $angle A$ is not $90^circ$ . By a similar logic, neither is $angle B$ .This means that $angle C=90^circ$ and $AC$ is perpendicular to $BC$ . Let C be the point $(n, n^2)$ . So the slope of $BC$ is the negative reciprocal of the slope of $AC$ , yielding $m+n=frac{1}{m-n}$ $Rightarrow$ $m^2-n^2=1$ .Because $m^2-n^2$ is the length of the altitude of triangle $ABC$ from $AB$ , and $2m$ is the length of $AB$ , the area of $triangle ABC=m(m^2-n^2)=2008$ . Since $m^2-n^2=1$ , $m=2008$ . Substituting, $2008^2-n^2=1$ $Rightarrow$ $n^2=2008^2-1=(2000+8)^2-1=4000000+32000+64-1=4032063$ , whose digits sum to $18 Rightarrow textbf{(C)}$ .
Let $h$ be the height of the pyramid and $a$ be the distance from $h$ to $CD$ . The side length of the base is $14$ . The heights of $triangle ABE$ and $triangle CDE$ are $2cdot105div14=15$ and $2cdot91div14=13$ , respectively. Consider a side view of the pyramid from $triangle BCE$ . We have a systems of equations through the Pythagorean Theorem: $13^2-(14-a)^2=h^2 15^2-a^2=h^2$ Setting them equal to each other and simplifying gives $-27+28a=225 implies a=9$ .Therefore, $h=sqrt{15^2-9^2}=12$ , and the volume of the pyramid is $frac{bh}{3}=frac{12cdot 196}{3}=boxed{784 Rightarrow E}$ .
Solution 1:

We need only concern ourselves with the imaginary portions of $f(1)$ and $f(i)$ (both of which must be 0). These are:

$begin{align*} Im(f(1)) & = i+iIm(alpha)+iIm(gamma) Im(f(i)) & = -i+iRe(alpha)+iIm(gamma) end{align*}$

Let $p=Im(gamma)$ and $q=Re{(gamma)},$ then we know $Im(alpha)=-p-1$ and $Re(alpha)=1-p.$ Therefore $[|alpha|+|gamma|=sqrt{(1-p)^2+(-1-p)^2}+sqrt{q^2+p^2}=sqrt{2p^2+2}+sqrt{p^2+q^2},]$ which reaches its minimum $sqrt 2$ when $p=q=0$ by the Trivial Inequality. Thus, the answer is $boxed B.$

Solution 2:

$f(1)=4+i+alpha+gamma$ $f(i)=-4-i+alpha cdot i +gamma$

Since $f(1)$ and $f(i)$ are both real we get, $[alpha+gamma=-i]$ $[alpha cdot i+gamma=i]$

Solving, we get $alpha=1-i$ , $gamma$ can be anything, to minimize the value we set $gamma=0$ , so then the answer is $sqrt{1^2+1^2}=sqrt{2}$ . Thus, the answer is $boxed{B}$
Pick a coordinate system where Michael's starting pail is $0$ and the one where the truck starts is $200$ . Let $M(t)$ and $T(t)$ be the coordinates of Michael and the truck after $t$ seconds. Let $D(t)=T(t)-M(t)$ be their (signed) distance after $t$ seconds. Meetings occur whenever $D(t)=0$ . We have $D(0)=200$ .The truck always moves for $20$ seconds, then stands still for $30$ . During the first $20$ seconds of the cycle the truck moves by $200$ feet and Michael by $100$ , hence during the first $20$ seconds of the cycle $D(t)$ increases by $100$ . During the remaining $30$ seconds $D(t)$ decreases by $150$ .From this observation it is obvious that after four full cycles, i.e. at $t=200$ , we will have $D(t)=0$ for the first time.During the fifth cycle, $D(t)$ will first grow from $0$ to $100$ , then fall from $100$ to $-50$ . Hence Michael overtakes the truck while it is standing at the pail.During the sixth cycle, $D(t)$ will first grow from $-50$ to $50$ , then fall from $50$ to $-100$ . Hence the truck starts moving, overtakes Michael on their way to the next pail, and then Michael overtakes the truck while it is standing at the pail.During the seventh cycle, $D(t)$ will first grow from $-100$ to $0$ , then fall from $0$ to $-150$ . Hence the truck meets Michael at the moment when it arrives to the next pail.Obviously, from this point on $D(t)$ will always be negative, meaning that Michael is already too far ahead. Hence we found all $boxed{5 Longrightarrow B}$ meetings.The movement of Michael and the truck is plotted below: Michael in blue, the truck in red. $[asy] import graph; size(400,300,IgnoreAspect); real[] xt = new real[21]; real[] yt = new real[21]; for (int i=0; i<11; ++i) xt[2*i]=50*i; for (int i=0; i<10; ++i) xt[2*i+1]=50*i+20; for (int i=0; i<11; ++i) yt[2*i]=200*(i+1); for (int i=0; i<10; ++i) yt[2*i+1]=200*(i+2); real[] xm={0,500}; real[] ym={0,2500}; draw(graph(xt,yt),red); draw(graph(xm,ym),blue); xaxis("$mathrm{time}$",Bottom,LeftTicks); yaxis("$mathrm{position}$",Left,LeftTicks); [/asy]$
Solution 1

Circles centered at $A$ and $B$ will overlap if $A$ and $B$ are closer to each other than if the circles were tangent. The circles are tangent when the distance between their centers is equal to the sum of their radii. Thus, the distance from $A$ to $B$ will be $2$ . Since $A$ and $B$ are separated by $1$ vertically, they must be separated by $sqrt{3}$ horizontally. Thus, if $|A_x-B_x|<sqrt{3}$ , the circles intersect.

Now, plot the two random variables $A_x$ and $B_x$ on the coordinate plane. Each variable ranges from $0$ to $2$ . The circles intersect if the variables are within $sqrt{3}$ of each other. Thus, the area in which the circles don't intersect is equal to the total area of two small triangles on opposite corners, each of area $frac{(2-sqrt{3})^2}{2}$ . We conclude the probability the circles intersect is: $[1-frac{(2-sqrt{3})^2}{4}=boxed{textbf{(E)}frac{4sqrt{3}-3}{4}}.]$

Solution 2

Two circles intersect if the distance between their centers is less than the sum of their radii. In this problem, $A$ and $B$ intersect iff $sqrt{(A_X-B_X)^2+(A_Y-B_Y)^2}leq2 Rightarrow (A_X-B_X)^2+1leq4 Rightarrow (A_X-B_X)leq sqrt{3}.$

In other words, the two chosen $x$ -coordinates must differ by no more than $sqrt{3}$ . To find this probability, we divide the problem into cases:

1) $A_X$ is on the interval $(0,2-sqrt{3})$ . The probability that $B_X$ falls within the desired range for a given $A_X$ is $A_X$ (on the left) $+sqrt{3}$ (on the right) all over $2$ (the range of possible values). The total probability for this range is the sum of all these probabilities of $B_X$ (over the range of $A_X$ ) divided by the total range of $A_X$ (which is $2$ ). Thus, the total probability for this interval is $[frac{1}{2}left(int_{0}^{2-sqrt{3}} frac{x+sqrt{3}}{2},dxright) =frac{1}{2}left(x^2/4+frac{xsqrt{3}}{2} Big |_{0}^{2-sqrt{3}}right)]$ $[= frac{1}{2}(frac{4-4sqrt{3}+3}{4} + sqrt{3}-frac{3}{2}) =frac{1}{8}.]$ 2) $A_X$ is on the interval $(2-sqrt{3},sqrt{3})$ . In this case, any value of $B_X$ will do, so the probability for the interval is simply $frac{sqrt{3}-(2-sqrt{3})}{2} = sqrt{3}-1$ .

3) $A_X$ is on the interval $(sqrt{3},2)$ . This is identical, by symmetry, to case 1.

The total probability is therefore $sqrt{3}-1+frac{1}{4} = frac{4sqrt{3}-3}{4} Rightarrow boxed{E}$

Solution 3

We first calculate the probability that the circles at are their maximum possible distance while still intersecting. Since the difference in heights is 1, and the two radii add up to 2 (at their point of tangency), we can see that the maximum possible distance for the two centers is $sqrt3$ . If we look at possible placements for the lower point, we see that at placement $(0,0)$ there is exactly $sqrt3$ of space wherein we can put the top point. Similarly, at point $(1,0)$ we can put the top point anywhere, resulting in $2$ of space. If one looks at a diagram (which I can't put here), we can see that the space available for the top point increases linearly from $(0,0)$ to $(2-sqrt3,0)$ . From then on to $(1,0)$ it stops at $2$ (this is symmetric for the other half of placements). If one draws a plot of the space available (which I again can't show here) with x determined by the x-value of the bottom point and y determined by space available for the top point, we notice two things: first, since for each (theoretically infinitesimally) small x-slice there is a line segment determining how much space there is available, if we sum up all of the line segments and divide by the total space (technically speaking by enumerating all the valid combinations and dividing by all of the general combinations), we will end up with a plot that looks like a rectangle with two small triangles cut out of it. Two, that since this is symmetric, we can just focus on the first half as the ratio of valid to total is the same. We see that the rectangle has a height of $2$ and a width of $1$ , thus its area is 2. The triangle's height is $2-sqrt3$ , and its width is the same thus its area is $(2-sqrt3)^2/2$ => $(7-4sqrt3)/2$ . Now we simply subtract to obtain $(4sqrt3-3)/2$ is the valid area, thus $(4sqrt3-3)/4 Rightarrow boxed{E}$ is our solution.
Auntie Em won't be able to park only when none of the four available spots touch. We can form a bijection between all such cases and the number of ways to pick four spots out of 13: since none of the spots touch, remove a spot from between each of the cars. From the other direction, given four spots out of 13, simply add a spot between each. So the probability she can park is $[1-frac{{13 choose 4}}{{16 choose 4}}=1-frac{13cdot12cdot11cdot10}{16cdot15cdot14cdot13}=1-frac{11}{28}={textbf{(E)}frac{17}{28}}.]$
Solution 1

Every factor of $10^n$ will be of the form $2^a times 5^b , aleq n , bleq n$ . Using the logarithmic property $log(a times b) = log(a)+log(b)$ , it suffices to count the total number of 2's and 5's running through all possible $(a,b)$ . For every factor $2^a times 5^b$ , there will be another $2^b times 5^a$ , so it suffices to count the total number of 2's occurring in all factors (because of this symmetry, the number of 5's will be equal). And since $log(2)+log(5) = log(10) = 1$ , the final sum will be the total number of 2's occurring in all factors of $10^n$ .

There are $n+1$ choices for the exponent of 5 in each factor, and for each of those choices, there are $n+1$ factors (each corresponding to a different exponent of 2), yielding $0+1+2+3...+n = frac{n(n+1)}{2}$ total 2's. The total number of 2's is therefore $frac{n cdot(n+1)^2}{2} = frac{n^3+2n^2+n}{2}$ . Plugging in our answer choices into this formula yields 11 (answer choice $mathrm{(A)}$ ) as the correct answer.

Solution 2

We are given $[log_{10}d_1 + log_{10}d_2 + ldots + log_{10}d_k = 792]$ The property $log(ab) = log(a)+log(b)$ now gives $[log_{10}(d_1 d_2cdotldots d_k) = 792]$ The product of the divisors is (from elementary number theory) $a^{d(n)/2}$ where $d(n)$ is the number of divisors. Note that $10^n = 2^ncdot 5^n$ , so $d(n) = (n + 1)^2$ . Substituting these values with $a = 10^n$ in our equation above, we get $n(n + 1)^2 = 1584$ , from whence we immediately obtain $framebox[1.2width]{(A)}$ as the correct answer.

Solution 3

For every divisor $d$ of $10^n$ , $d le sqrt{10^n}$ , we have $log d + log frac{10^n}{d} = log 10^n = n$ . There are $left lfloor frac{(n+1)^2}{2} right rfloor$ divisors of $10^n = 2^n times 5^n$ that are $le sqrt{10^n}$ . After casework on the parity of $n$ , we find that the answer is given by $n times frac{(n+1)^2}{2} = 792 Longrightarrow n = 11 mathrm{(A)}$ .

Solution 4

The sum is $[sum_{p=0}^{n}sum_{q=0}^{n} log(2^p5^q) = sum_{p=0}^{n}sum_{q=0}^{n}(plog(2)+qlog(5))]$ $[= sum_{p=0}^{n} ((n+1)plog(2) + frac{n(n+1)}{2}log(5))]$ $[= frac{n(n+1)^2}{2} log(2) + frac{n(n+1)^2}{2} log(5)]$ $[= frac{n(n+1)^2}{2}]$ Trying for answer choices we get $n=11$
Solution 1

Let $a_n=|A_{n-1}A_n|$ . We need to rewrite the recursion into something manageable. The two strange conditions, $B$ 's lie on the graph of $y=sqrt{x}$ and $A_{n-1}B_nA_n$ is an equilateral triangle, can be compacted as follows: $[left(a_nfrac{sqrt{3}}{2}right)^2=frac{a_n}{2}+a_{n-1}+a_{n-2}+cdots+a_1]$ which uses $y^2=x$ , where $x$ is the height of the equilateral triangle and therefore $frac{sqrt{3}}{2}$ times its base.

The relation above holds for $n=k$ and for $n=k-1$ $(k>1)$ , so $[left(a_kfrac{sqrt{3}}{2}right)^2-left(a_{k-1}frac{sqrt{3}}{2}right)^2=]$ $[=left(frac{a_k}{2}+a_{k-1}+a_{k-2}+cdots+a_1right)-left(frac{a_{k-1}}{2}+a_{k-2}+a_{k-3}+cdots+a_1right)]$ Or, $[a_k-a_{k-1}=frac23]$ This implies that each segment of a successive triangle is $frac23$ more than the last triangle. To find $a_{1}$ , we merely have to plug in $k=1$ into the aforementioned recursion and we have $a_{1} - a_{0} = frac23$ . Knowing that $a_{0}$ is $0$ , we can deduce that $a_{1} = 2/3$ .Thus, $a_n=frac{2n}{3}$ , so $A_0A_n=a_n+a_{n-1}+cdots+a_1=frac{2}{3} cdot frac{n(n+1)}{2} = frac{n(n+1)}{3}$ . We want to find $n$ so that $n^2<300<(n+1)^2$ . $n=boxed{17}$ is our answer.

Solution 2

Consider two adjacent equilateral triangles obeying the problem statement. For each, drop an altitude to the $x$ axis and denote the resulting heights $h_n$ and $h_{n+1}$ . From 30-60-90 rules, the difference between the base of these altitudes is $[frac{h_{n+1}}{sqrt{3}}+frac{h_n}{sqrt{3}} Rightarrow frac{h_{n+1}+h_n}{sqrt{3}}]$

But the square root curve means that this distance is also expressible as $h_{n+1}^2-h_n^2$ (the $x$ coordinates are the squares of the heights). Setting these expressions equal and dividing throughout by $h_{n+1}+h_n$ leaves $h_{n+1}-h_n=frac{1}{sqrt{3}}$ . So the difference in height of successive triangles is $frac{1}{sqrt{3}}$ , meaning their bases are $2/3$ wider and wider each time. From here, one can proceed as in Solution 1 to arrive at $n=boxed{17}$ .
Note: In the image AB and CD have been swapped from their given lengths in the problem. However, this doesn't affect any of the solving.Drop perpendiculars to $CD$ from $A$ and $B$ , and call the intersections $X,Y$ respectively. Now, $DA^2-BC^2=(7-5)(7+5)=DX^2-CY^2$ and $DX+CY=19-11=8$ . Thus, $DX-CY=3$ . We conclude $DX=frac{11}{2}$ and $CY=frac{5}{2}$ . To simplify things even more, notice that $90^{circ}=frac{angle D+angle A}{2}=180^{circ}-angle APD$ , so $angle P=angle Q=90^{circ}$ .Also, $[sin(angle PAD)=sin(frac12angle XDA)=sqrt{frac{1-cos(angle XDA)}{2}}=sqrt{frac{3}{28}}]$ So the area of $triangle APD$ is: $[Rcdot csin asin b =frac{7cdot7}{2}sqrt{frac{3}{28}}sqrt{1-frac{3}{28}}=frac{35}{8}sqrt{3}]$ Over to the other side: $triangle BCY$ is $30-60-90$ , and is therefore congruent to $triangle BCQ$ . So $[BCQ]=frac{5cdot5sqrt{3}}{8}$ .The area of the hexagon is clearly $[ABCD]-([BCQ]+[APD])$ $[=frac{15cdot5sqrt{3}}{2}-frac{60sqrt{3}}{8}=30sqrt{3}impliesboxed{B}]$ Note: Once $DY$ is found, there is no need to do the trig. Notice that the hexagon consists of two trapezoids, ABPQ and CDPQ. PQ = (19-7-5 +11)/2 = 9. The height is one half of $BY$ which is $frac{5sqrt{3}}{4}$ . So the area is $[frac{1}{2}frac{5sqrt{3}}{4}(19+9+11+9)=30sqrt{3}]$

Solution 2

Let $AP$ and $BQ$ meet $CD$ at $X$ and $Y$ , respectively.

Since $angle APD=90^{circ}$ , $angle ADP=angle XDP$ , and they share $DP$ , triangles $APD$ and $XPD$ are congruent.

By the same reasoning, we also have that triangles $BQC$ and $YQC$ are congruent.

Hence, we have $[ABQCDP]=[ABYX]+frac{[ABCD]-[ABYX]}{2}=frac{[ABCD]+[ABYX]}{2}$ .

If we let the height of the trapezoid be $x$ , we have $[ABQCDP]=frac{frac{11+19}{2}cdot x+frac{11+7}{2}cdot x}{2}=12x$ .

Thusly, if we find the height of the trapezoid and multiply it by 12, we will be done.

Let the projections of $A$ and $B$ to $CD$ be $A'$ and $B'$ , respectively.

We have $DA'+CB'=19-11=8$ , $DA'=sqrt{DA^2-AA'^2}=sqrt{49-x^2}$ , and $CB'=sqrt{CB^2-BB'^2}=sqrt{25-x^2}$ .

Therefore, $sqrt{49-x^2}+sqrt{25-x^2}=8$ . Solving this, we easily get that $x=frac{5sqrt{3}}{2}$ .

Multiplying this by 12, we find that the area of hexagon $ABQCDP$ is $30sqrt{3}$ , which corresponds to answer choice $boxed{B}$ .

Solution 3

$[asy] unitsize(0.6cm); import olympiad; pair A,B,C,D,P,Q,M,N,W,X,Y,Z; A=(11/2,5sqrt(3)/2); B=(33/2,5sqrt(3)/2); C=(19,0); D=(0,0); P=incenter(A,D,(99999,5sqrt(3)/4)); Q=incenter(B,C,(-99999,5sqrt(3)/4)); W=P+(0,5sqrt(3)/4); X=P-(0,5sqrt(3)/4); Y=Q+(0,5sqrt(3)/4); Z=Q-(0,5sqrt(3)/4); M=reflect(A,P)*W; N=reflect(B,Q)*Y; draw(A--B--C--D--cycle); draw(A--P--D); draw(B--Q--C); label("$A$",A,dir(135)); label("$B$",B,dir(45)); label("$C$",C,dir(315)); label("$D$",D,dir(225)); dot("$P$",P,dir(0)); dot("$Q$",Q,dir(180)); draw(W--X); draw(Y--Z); draw(M--P); draw(N--Q); label("$11$",midpoint(A--B),dir(90)); label("$5$",midpoint(B--C),dir(45)); label("$19$",midpoint(C--D),dir(270)); label("$7$",midpoint(D--A),dir(135)); label("$x$",midpoint(P--W),dir(0)); label("$x$",midpoint(P--X),dir(0)); label("$x$",midpoint(P--M),dir(225)); label("$x$",midpoint(Q--Y),dir(180)); label("$x$",midpoint(Q--Z),dir(180)); label("$x$",midpoint(Q--N),dir(315)); draw(rightanglemark(P,W,B,12.5)); draw(rightanglemark(P,X,C,12.5)); draw(rightanglemark(P,M,D,12.5)); draw(rightanglemark(Q,Y,A,12.5)); draw(rightanglemark(Q,Z,D,12.5)); draw(rightanglemark(Q,N,C,12.5)); [/asy]$

Since point $P$ is the intersection of the angle bisectors of $angle A$ and $angle D$ , $P$ is equidistant from $overline{AB}$ , $overline{AD}$ , and $overline{CD}$ . Likewise, point $Q$ is equidistant from $overline{AB}$ , $overline{BC}$ , and $overline{CD}$ . Because both points $P$ and $Q$ are equidistant from $overline{AB}$ and $overline{CD}$ and the distance between $overline{AB}$ and $overline{CD}$ is constant, the common distances from each of the points to the mentioned segments is equal for $P$ and $Q$ . Call this distance $x$ .

The distance between a point and a line is the length of the segment perpendicular to the line with one endpoint on the line and the other on the point. This means the altitude from $P$ to $overline{AD}$ is $x$ , so the area of $triangle ADP$ is equal to $frac12cdot ADcdot x=frac72x$ . Similarly, the area of $triangle BCQ$ is $frac12cdot BCcdot x=frac52x$ . The altitude of the trapezoid is $2x$ , because it is the sum of the distances from either $P$ or $Q$ to $overline{AB}$ and $overline{CD}$ . This means the area of trapezoid $ABCD$ is $frac12(AB+CD)cdot2x=frac12(11+19)cdot2x=30x$ . Now, the area of hexagon $ABQCDP$ is the area of trapezoid $ABCD$ , minus the areas of triangles $ADP$ and $BCQ$ . This is $30x-frac72x-frac52x=24x$ . Now it remains to find $x$ .

$[asy] unitsize(0.6cm); import olympiad; pair A,B,C,D,R,S; A=(11/2,5sqrt(3)/2); B=(33/2,5sqrt(3)/2); C=(19,0); D=(0,0); R=(11/2,0); S=(33/2,0); draw(A--B--C--D--cycle); draw(A--R); draw(B--S); label("$A$",A,dir(135)); label("$B$",B,dir(45)); label("$C$",C,dir(315)); label("$D$",D,dir(225)); label("$R$",R,dir(270)); label("$S$",S,dir(270)); label("$11$",midpoint(A--B),dir(90)); label("$5$",midpoint(B--C),dir(45)); label("$11$",midpoint(R--S),dir(270)); label("$7$",midpoint(D--A),dir(135)); label("$r$",midpoint(R--D),dir(270)); label("$s$",midpoint(C--S),dir(270)); label("$19$",midpoint(C--D),5*dir(270)); label("$2x$",midpoint(A--R),dir(0)); label("$2x$",midpoint(B--S),dir(180)); draw(rightanglemark(A,R,D,15)); draw(rightanglemark(B,S,C,15)); [/asy]$

We let $R$ and $S$ be the feet of the altitudes of $A$ and $B$ , respectively, to $overline{CD}$ . We define $r=RD$ and $s=SC$ . We know that $AB=RS$ , so $RS=11$ and $r+s=19-11=8$ . By the Pythagorean Theorem on $triangle ADR$ and $triangle BCS$ , we get $r^2+(2x)^2=7^2$ and $s^2+(2x)^2=5^2$ , respectively. Subtracting the second equation from the first gives us $r^2-s^2=49-25=24$ . The left hand side of this equation is a difference of squares and factors to $(r+s)(r-s)$ . We know that $r+s=8$ , so $r-s=frac{24}8=3$ . Now we can solve for $r$ by adding the two equations we just got to see that $2r=11$ , or $r=frac{11}2$ .

We now solve for $x$ . We know that $r^2+(2x)^2=49$ , so $(2x)^2=49-left(frac{11}2right)^2=frac{75}4$ and $2x=frac{5sqrt3}2$ . We multiply both sides of this equation by $12$ to get $24x=30sqrt3$ . However, the area of hexagon $ABQCDP$ is $24x$ , so the answer is $30sqrt 3$ , or answer choice $boxed{B}$ .

Solution 4

$[asy] import olympiad; unitsize(0.5cm); pair A, B, C, D; A = 5*(Cos(120), Sin(120)); B = A + (-11, 0); C = origin + (-19, 0); D = origin; label("$A$", A, dir(30)); label("$B$", B, dir(150)); label("$C$", C, dir(150)); label("$D$", D, dir(30)); pair E, F, G, H; E = bisectorpoint(B, A, D); F = bisectorpoint(A, B, C); G = bisectorpoint(B, C, D); H = bisectorpoint(C, D, A); pair P, Q; P = extension(A, E, D, H); Q = extension(B, F, C, G); dot("$P$", P, dir(20)); dot("$Q$", Q, dir(150)); pair W, X, Y, Z; W = extension(A, P, D, C); X = extension(B, Q, C, D); Y = extension(C, Q, A, B); Z = extension(D, P, A, B); label("$W$", W, dir(100)); label("$X$", X, dir(60)); label("$Y$", Y, dir(50)); label("$Z$", Z, dir(140)); draw(A--W--X--B--Y--C--D--Z--B--C--Y--A--D); [/asy]$

Let $W, X, Y, Z = overline{AP} cap overline{CD}, overline{BQ} cap overline{CD}, overline{CQ} cap overline{AB}, overline{DP} cap overline{AB}$ respectively. Since $angle{DCQ} = angle{BCQ}, angle{CBQ} = angle{ABQ}$ we have $angle{QCB} + angle{CBQ} = 90 iff overline{BX} perp overline{CY};$ similarly we get $overline{AW} perp overline{DZ}.$ Thus, $overline{BQ}$ is both an angle bisector and altitude of $triangle{CBY}$ so $BC = BY.$ Using the same logic on $triangle{BCX}$ gives $BC = BX iff BYXC$ is a rhombus; similarly, $ADWZ$ is a rhombus. Then, $[ABQCDP] = [ABCD] - frac{1}{4}left([BYXC] + [ADWZ]right) = 15h - frac{1}{4}(7h + 12h) = 12h$ where $h$ is the height of trapezoid $ABCD.$ Finding $h$ is the same as finding the altitude to the side of length $8$ in a $5-7-8$ triangle, and using Heron's, the area of such a triangle is $sqrt{10(5)(3)(2)} = 10 sqrt{3} = 4h iff h = frac{5sqrt{3}}{2}.$ Multiply to get our answer if $boxed{B}.$

Solution 5

Like above solutions, find out the height of $ABCD$ is $frac{5 sqrt{3}}{2}.$ Let $M$ be the intersection of the line through $Q$ and parallel to $AB,$ and $N$ the intersection of the line through $P$ and parallel to $AB.$ Angle chasing shows that $M$ is the midpoint of $BC$ and $N$ midpoint of $AD.$ Then from midline theorem, $M, Q, N$ are collinear, and likewise for $N, P, M.$ Thus, the line through $PQ$ is in fact the midline of $ABCD.$

Let $BQ cap CD = X, AP cap CD = Y.$ Then, angle chasing shows that $CQ$ not only bisects $BX,$ but is also perpendicular to it. This makes it a perpendicular bisector. The same is true for $DP$ and $AY.$ Thus, $CX = CB = 5,$ and $DY = DA = 7.$ This means $XY = 19 - 5 - 7 = 7.$ We can now find $PQ$ as the midline of $ABXY.$ Thus, $PQ = frac{1}{2} (11+7) = 9.$

Now, the answer is simply finding the area of $ABQP$ plus area of $CDPQ.$ This is $frac{1}{2} cdot frac{5 sqrt{3}}{2} cdot frac{11+9}{2} + frac{1}{2} cdot frac{5 sqrt{3}}{2} cdot frac{19+9}{2} = boxed{30 sqrt{3}}.$