- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2008 AMC12A 真题及答案详细解析
2008 AMC 12 A 真题
真题及解析
Problem 1
A bakery owner turns on his doughnut machine at ![]() . At
. At ![]() the machine has completed one third of the day's job. At what time will the doughnut machine complete the job?
the machine has completed one third of the day's job. At what time will the doughnut machine complete the job?
![]()
Problem 2
What is the reciprocal of ![]() ?
?
![]()
Problem 3
Suppose that ![]() of
of ![]() bananas are worth as much as
bananas are worth as much as ![]() oranges. How many oranges are worth as much as
oranges. How many oranges are worth as much as ![]() of
of ![]() bananas?
bananas?
![]()
Problem 4
Which of the following is equal to the product![]()
![]()
Problem 5
Suppose that![]() is an integer. Which of the following statements must be true about
is an integer. Which of the following statements must be true about ![]() ?
?

Problem 6
Heather compares the price of a new computer at two different stores. Store ![]() offers
offers ![]() off the sticker price followed by a
off the sticker price followed by a ![]() rebate, and store
rebate, and store ![]() offers
offers ![]() off the same sticker price with no rebate. Heather saves
off the same sticker price with no rebate. Heather saves ![]() by buying the computer at store
by buying the computer at store ![]() instead of store
instead of store ![]() . What is the sticker price of the computer, in dollars?
. What is the sticker price of the computer, in dollars?
![]()
Problem 7
While Steve and LeRoy are fishing 1 mile from shore, their boat springs a leak, and water comes in at a constant rate of 10 gallons per minute. The boat will sink if it takes in more than 30 gallons of water. Steve starts rowing toward the shore at a constant rate of 4 miles per hour while LeRoy bails water out of the boat. What is the slowest rate, in gallons per minute, at which LeRoy can bail if they are to reach the shore without sinking?
![]()
Problem 8
What is the volume of a cube whose surface area is twice that of a cube with volume 1?
![]()
Problem 9
Older television screens have an aspect ratio of ![]() . That is, the ratio of the width to the height is
. That is, the ratio of the width to the height is ![]() . The aspect ratio of many movies is not
. The aspect ratio of many movies is not ![]() , so they are sometimes shown on a television screen by "letterboxing" - darkening strips of equal height at the top and bottom of the screen, as shown. Suppose a movie has an aspect ratio of
, so they are sometimes shown on a television screen by "letterboxing" - darkening strips of equal height at the top and bottom of the screen, as shown. Suppose a movie has an aspect ratio of ![]() and is shown on an older television screen with a
and is shown on an older television screen with a ![]() -inch diagonal. What is the height, in inches, of each darkened strip?
-inch diagonal. What is the height, in inches, of each darkened strip?
![[asy]unitsize(1mm); filldraw((0,0)--(21.6,0)--(21.6,2.7)--(0,2.7)--cycle,grey,black); filldraw((0,13.5)--(21.6,13.5)--(21.6,16.2)--(0,16.2)--cycle,grey,black); draw((0,0)--(21.6,0)--(21.6,16.2)--(0,16.2)--cycle);[/asy]](https://latex.artofproblemsolving.com/4/9/9/4994e8ffcb62ccc25ab593f3852cfd9b2fb7ba26.png)
![]()
Problem 10
Doug can paint a room in ![]() hours. Dave can paint the same room in
hours. Dave can paint the same room in ![]() hours. Doug and Dave paint the room together and take a one-hour break for lunch. Let
hours. Doug and Dave paint the room together and take a one-hour break for lunch. Let ![]() be the total time, in hours, required for them to complete the job working together, including lunch. Which of the following equations is satisfied by
be the total time, in hours, required for them to complete the job working together, including lunch. Which of the following equations is satisfied by ![]() ?
?

Problem 11
Three cubes are each formed from the pattern shown. They are then stacked on a table one on top of another so that the ![]() visible numbers have the greatest possible sum. What is that sum?
visible numbers have the greatest possible sum. What is that sum?
![[asy] unitsize(.8cm); pen p = linewidth(1); draw(shift(-2,0)*unitsquare,p); label("1",(-1.5,0.5)); draw(shift(-1,0)*unitsquare,p); label("2",(-0.5,0.5)); draw(unitsquare,p); label("32",(0.5,0.5)); draw(shift(1,0)*unitsquare,p); label("16",(1.5,0.5)); draw(shift(0,1)*unitsquare,p); label("4",(0.5,1.5)); draw(shift(0,-1)*unitsquare,p); label("8",(0.5,-0.5)); [/asy]](https://latex.artofproblemsolving.com/a/3/2/a32f7c9839807c1cb204fd5a2f87f33747244a18.png)
![]()
Problem 12
A function ![]() has domain
has domain ![]() and range
and range ![]() . (The notation
. (The notation ![]() denotes
denotes ![]() .) What are the domain and range, respectively, of the function
.) What are the domain and range, respectively, of the function ![]() defined by
defined by ![]() ?
?
![]()
Problem 13
Points ![]() and
and ![]() lie on a circle centered at
lie on a circle centered at ![]() , and
, and ![]() . A second circle is internally tangent to the first and tangent to both
. A second circle is internally tangent to the first and tangent to both ![]() and
and ![]() . What is the ratio of the area of the smaller circle to that of the larger circle?
. What is the ratio of the area of the smaller circle to that of the larger circle?
![]()
Problem 14
What is the area of the region defined by the inequality ![]() ?
?
![]()
Problem 15
Let ![]() . What is the units digit of
. What is the units digit of ![]() ?
?
![]()
Problem 16
The numbers ![]() ,
, ![]() , and
, and ![]() are the first three terms of an arithmetic sequence, and the
are the first three terms of an arithmetic sequence, and the ![]() term of the sequence is
term of the sequence is ![]() . What is
. What is ![]() ?
?
![]()
Problem 17
Let ![]() be a sequence determined by the rule
be a sequence determined by the rule ![]() if
if ![]() is even and
is even and ![]() if
if ![]() is odd. For how many positive integers
is odd. For how many positive integers ![]() is it true that
is it true that ![]() is less than each of
is less than each of ![]() ,
, ![]() , and
, and ![]() ?
?
![]()
Problem 18
A triangle ![]() with sides
with sides ![]() ,
, ![]() ,
, ![]() is placed in the three-dimensional plane with one vertex on the positive
is placed in the three-dimensional plane with one vertex on the positive ![]() axis, one on the positive
axis, one on the positive ![]() axis, and one on the positive
axis, and one on the positive ![]() axis. Let
axis. Let ![]() be the origin. What is the volume of
be the origin. What is the volume of ![]() ?
?
![]()
Problem 19
In the expansion of![]() what is the coefficient of
what is the coefficient of ![]() ?
?
![]()
Problem 20
Triangle ![]() has
has ![]() ,
, ![]() , and
, and ![]() . Point
. Point ![]() is on
is on ![]() , and
, and ![]() bisects the right angle. The inscribed circles of
bisects the right angle. The inscribed circles of ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively. What is
, respectively. What is ![]() ?
?

Problem 21
A permutation ![]() of
of ![]() is heavy-tailed if
is heavy-tailed if ![]() . What is the number of heavy-tailed permutations?
. What is the number of heavy-tailed permutations?
![]()
Problem 22
A round table has radius ![]() . Six rectangular place mats are placed on the table. Each place mat has width
. Six rectangular place mats are placed on the table. Each place mat has width ![]() and length
and length ![]() as shown. They are positioned so that each mat has two corners on the edge of the table, these two corners being end points of the same side of length
as shown. They are positioned so that each mat has two corners on the edge of the table, these two corners being end points of the same side of length ![]() . Further, the mats are positioned so that the inner corners each touch an inner corner of an adjacent mat. What is
. Further, the mats are positioned so that the inner corners each touch an inner corner of an adjacent mat. What is ![]() ?
?
![[asy]unitsize(4mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=(-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle; draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); label("(x)",(-1.55,2.1),E); label("(1)",(-0.5,3.8),S);[/asy]](https://latex.artofproblemsolving.com/4/5/5/455ee9e9f5150b8651dd85c1adc2f62d3193a852.png)
![]()
Problem 23
The solutions of the equation ![]() are the vertices of a convex polygon in the complex plane. What is the area of the polygon?
are the vertices of a convex polygon in the complex plane. What is the area of the polygon?
![]()
Problem 24
Triangle ![]() has
has ![]() and
and ![]() . Point
. Point ![]() is the midpoint of
is the midpoint of ![]() . What is the largest possible value of
. What is the largest possible value of ![]() ?
?
![]()
Problem 25
A sequence ![]() ,
, ![]() ,
, ![]() ,
, ![]() of points in the coordinate plane satisfies
of points in the coordinate plane satisfies
![]() for
for ![]() .
.
Suppose that ![]() . What is
. What is ![]() ?
?
![]()
2008 AMC12 A 真题答案详细解析
- The machine completes one-third of the job in
 hours. Thus, the entire job is completed in
hours. Thus, the entire job is completed in  hours.
hours.
Since the machine was started at , the job will be finished
, the job will be finished  hours later, at
hours later, at  . The answer is
. The answer is  .
. -
Solution 1
Here's a cheapshot: Obviously,
 is greater than
is greater than  . Therefore, its reciprocal is less than
. Therefore, its reciprocal is less than  , and the answer must be
, and the answer must be  .
.Solution 2
 .
. - If
 , then
, then  .
. -
Solution 1

 .
.Solution 2
Notice that everything cancels out except for
 in the numerator and
in the numerator and  in the denominator.
in the denominator.Thus, the product is
 , and the answer is
, and the answer is  .
. ![[frac{2x}{3}-frac{x}{6}quadLongrightarrowquadfrac{4x}{6}-frac{x}{6}quadLongrightarrowquadfrac{3x}{6}quadLongrightarrowquadfrac{x}{2}]](https://latex.artofproblemsolving.com/6/b/f/6bfcc085910df27c7cc1f6881760996e40ed36ff.png)
For to be an integer,
to be an integer,  must be even, but not necessarily divisible by
must be even, but not necessarily divisible by  . Thus, the answer is
. Thus, the answer is  .
.-
Solution 1
Let the sticker price be
 .
.The price of the computer is
 at store
at store  , and
, and  at store
at store 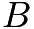 .
.Heather saves

 at store
at store  , so
, so  .
.Solving, we find
 , and the thus answer is
, and the thus answer is  .
.Solution 2
The
 in store
in store  is
is  better than the additional
better than the additional  off at store
off at store 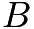 .
.Thus the
 off is equal to
off is equal to  -
- 

 , and therefore the sticker price is
, and therefore the sticker price is  .
. - It will take
 of an hour or
of an hour or  minutes to get to shore.Since only
minutes to get to shore.Since only  gallons of water can enter the boat, only
gallons of water can enter the boat, only  net gallons can enter the boat per minute.Since
net gallons can enter the boat per minute.Since  gallons of water enter the boat each minute, LeRoy must bail
gallons of water enter the boat each minute, LeRoy must bail  gallons per minute
gallons per minute  .
. - A cube with volume
 has a side of length
has a side of length ![$sqrt[3]{1}=1$](https://latex.artofproblemsolving.com/3/c/6/3c65bfc5db8bea84fcd769f69191c1c492e6718f.png) and thus a surface area of
and thus a surface area of  .A cube whose surface area is
.A cube whose surface area is  has a side of length
has a side of length  and a volume of
and a volume of  .
. - Let the width and height of the screen be
 and
and  respectively, and let the width and height of the movie be
respectively, and let the width and height of the movie be  and
and  respectively.By the Pythagorean Theorem, the diagonal is
respectively.By the Pythagorean Theorem, the diagonal is  . So
. So  .Since the movie and the screen have the same width,
.Since the movie and the screen have the same width,  .Thus, the height of each strip is
.Thus, the height of each strip is  .
. -
Solution 1
Doug can paint
 of a room per hour, Dave can paint
of a room per hour, Dave can paint  of a room in an hour, and the time they spend working together is
of a room in an hour, and the time they spend working together is  .
.Since rate times time gives output,

Solution 2
If one person does a job in
 hours and another person does a job in
hours and another person does a job in  hours, the time it takes to do the job together is
hours, the time it takes to do the job together is  hours.
hours.Since Doug paints a room in 5 hours and Dave paints a room in 7 hours, they both paint in
 hours. They also take 1 hour for lunch, so the total time
hours. They also take 1 hour for lunch, so the total time  hours.
hours.Looking at the answer choices,
 is the only one satisfied by
is the only one satisfied by  .
. - To maximize the sum of the
 faces that are showing, we can minimize the sum of the numbers of the
faces that are showing, we can minimize the sum of the numbers of the  faces that are not showing.The bottom
faces that are not showing.The bottom  cubes each have a pair of opposite faces that are covered up. When the cube is folded,
cubes each have a pair of opposite faces that are covered up. When the cube is folded,  ;
;  ; and
; and  are opposite pairs. Clearly
are opposite pairs. Clearly  has the smallest sum.The top cube has 1 number that is not showing. The smallest number on a face is
has the smallest sum.The top cube has 1 number that is not showing. The smallest number on a face is  .So, the minimum sum of the
.So, the minimum sum of the  unexposed faces is
unexposed faces is  . Since the sum of the numbers on all the cubes is
. Since the sum of the numbers on all the cubes is  , the maximum possible sum of
, the maximum possible sum of  visible numbers is
visible numbers is  .
.  is defined if
is defined if  is defined. Thus the domain is all
is defined. Thus the domain is all ![$x| x + 1 in [0,2] rightarrow x in [ - 1,1]$](https://latex.artofproblemsolving.com/d/8/b/d8b6624181948180d27595212f0b42c0aceed048.png) .Since
.Since ![$f(x + 1) in [0,1]$](https://latex.artofproblemsolving.com/6/2/9/629de8878872a37847132bd922824fc8b712810d.png) ,
, ![$- f(x + 1) in [ - 1,0]$](https://latex.artofproblemsolving.com/c/c/9/cc930a8e58693cb8571f0405363867f1f5d76983.png) . Thus
. Thus ![$g(x) = 1 - f(x + 1) in [0,1]$](https://latex.artofproblemsolving.com/8/8/3/8834c52dfda63c5f6ffb6a790b72dadf548aa29b.png) is the range of
is the range of  .Thus the answer is
.Thus the answer is ![$[- 1,1],[0,1] longrightarrow boxed{B}$](https://latex.artofproblemsolving.com/1/f/0/1f0db379b8d21a2b1747508605654327f5c0a7e9.png) .
.![[asy]size(200); defaultpen(fontsize(10)); pair O=(0,0), A=(3,0), B=(3/2,3/2*3^.5), C=(3^.5,1), D=(3^.5,0), F=(1.5*3^.5,1.5); picture p = new picture; draw(p,Circle(O,0.2)); clip(p,O--C--A--cycle); add(p); draw(Circle(O,3)); dot(A); dot(B); dot(C); dot(O); draw(A--O--B); draw(O--C--D); draw(C--F); draw(D-(0.2,0)--D-(0.2,-0.2)--D-(0,-0.2)); draw(Circle(C,1)); label("(30^{circ})",(0.65,0.15),O); label("(r)",(C+D)/2,E); label("(2r)",(O+C)/2,NNE); label("(O)",O,SW); label("(r)",(C+F)/2,SE); label("(R)",(O+A)/2-(0,0.3),S); label("(P)",C,NW); label("(Q)",D,SE);[/asy]](https://latex.artofproblemsolving.com/d/3/1/d3142ba25b2b5802e567ff06a53c2a14a3afb759.png) Let
Let  be the center of the small circle with radius
be the center of the small circle with radius  , and let
, and let  be the point where the small circle is tangent to
be the point where the small circle is tangent to  . Also, let
. Also, let  be the point where the small circle is tangent to the big circle with radius
be the point where the small circle is tangent to the big circle with radius  .Then
.Then  is a right triangle, and a
is a right triangle, and a  triangle at that. Therefore,
triangle at that. Therefore,  .Since
.Since  , we have
, we have  , or
, or  , or
, or  .Then the ratio of areas will be
.Then the ratio of areas will be  squared, or
squared, or  .
.- Area is invariant under translation, so after translating left
 and up
and up  units, we have the inequality
units, we have the inequality![[|3x| + |2y|leq 3]](https://latex.artofproblemsolving.com/a/1/9/a19f2f8dd7ca0806a76ba3bfc99a47c9ab449dbb.png) which forms a diamond centered at the origin and vertices at
which forms a diamond centered at the origin and vertices at  . Thus the diagonals are of length
. Thus the diagonals are of length  and
and  . Using the formula
. Using the formula  , the answer is
, the answer is  .
.  .So,
.So,  . Since
. Since  is a multiple of four and the units digit of powers of two repeat in cycles of four,
is a multiple of four and the units digit of powers of two repeat in cycles of four,  .Therefore,
.Therefore,  . So the units digit is
. So the units digit is  .
.-
Solution 1
Let
 and
and  .
.The first three terms of the arithmetic sequence are
 ,
,  , and
, and  , and the
, and the  term is
term is  .
.Thus,
 .
.Since the first three terms in the sequence are
 ,
,  , and
, and  , the
, the  th term is
th term is  .
.Thus the
 term is
term is  .
.Solution 2
If
 ,
,  , and
, and  are in arithmetic progression, then
are in arithmetic progression, then  ,
,  , and
, and  are in geometric progression. Therefore,
are in geometric progression. Therefore,![[a^2b^5=a^3b^3 Rightarrow a=b^2]](https://latex.artofproblemsolving.com/2/6/7/267dc9ebb14c8c501f62a7892f64e67ce84e034d.png)
Therefore,
 ,
,  , therefore the 12th term in the sequence is
, therefore the 12th term in the sequence is 
Solution 3





- All positive integers can be expressed as
 ,
,  ,
,  , or
, or  , where
, where  is a nonnegative integer.
is a nonnegative integer.
- If
 , then
, then  .
.
- If
 , then
, then  ,
,  , and
, and  .
.
- If
 , then
, then  .
.
- If
 , then
, then  ,
,  , and
, and  .
.
Since
 , every positive integer
, every positive integer  will satisfy
will satisfy  .
.Since one fourth of the positive integers
 can be expressed as
can be expressed as  , where
, where  is a nonnegative integer, the answer is
is a nonnegative integer, the answer is  .
.Alternate Solution
After checking the first few
 such as
such as  ,
,  through
through  , we can see that the only
, we can see that the only  that satisfy the conditions are odd numbers that when tripled and added 1 to, are double an odd number. For example, for
that satisfy the conditions are odd numbers that when tripled and added 1 to, are double an odd number. For example, for  , we notice the sequence yields
, we notice the sequence yields  ,
,  , and
, and  , a valid sequence.
, a valid sequence.So we can set up an equation,
 where x is equal to
where x is equal to  . Rearranging the equation yields
. Rearranging the equation yields  . Experimenting yields that every 4th
. Experimenting yields that every 4th  after 3 creates an integer, and thus satisfies the sequence condition. So the number of valid solutions is equal to
after 3 creates an integer, and thus satisfies the sequence condition. So the number of valid solutions is equal to  .
. - If
![[asy] defaultpen(fontsize(8)); draw((0,10)--(0,0)--(8,0));draw((-3,-4)--(0,0));draw((0,10)--(-3,-4)--(8,0)--cycle); label("A",(8,0),(1,0));label("B",(0,10),(0,1));label("C",(-3,-4),(-1,-1));label("O",(0,0),(1,1)); label("$a$",(4,0),(0,1));label("$b$",(0,5),(1,0));label("$c$",(-1.5,-2),(1,0)); label("$5$",(4,5),(1,1));label("$6$",(-1.5,3),(-1,0));label("$7$",(2.5,-2),(1,-1)); [/asy]](https://latex.artofproblemsolving.com/b/4/8/b48d9f2414f67d68d2e53886e0726e31626cd919.png)
 be on the
be on the  axis,
axis, 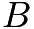 be on the
be on the  axis, and
axis, and  be on the
be on the  axis, and let
axis, and let  have respective lengths of 5, 6, and 7. Let
have respective lengths of 5, 6, and 7. Let  denote the lengths of segments
denote the lengths of segments  respectively. Then by the Pythagorean Theorem,
respectively. Then by the Pythagorean Theorem, so
so  ; similarly,
; similarly,  and
and  . Since
. Since  ,
,  , and
, and  are mutually perpendicular, the tetrahedron's volume is
are mutually perpendicular, the tetrahedron's volume is![[abc/6]](https://latex.artofproblemsolving.com/b/7/4/b74807ac0ee77d6e400564a0e5622c8fa9371d61.png) because we can consider the tetrahedron to be a right triangular pyramid.
because we can consider the tetrahedron to be a right triangular pyramid.![[abc/6 = sqrt{a^2b^2c^2}/6 = frac{sqrt{19 cdot 6 cdot 30}}{6} = sqrt{95},]](https://latex.artofproblemsolving.com/f/a/4/fa42628f26cbd85dad184ed745d0a3699e3afaa9.png) which is answer choice
which is answer choice  .
.-
Solution 1
Let
 and
and  . We are expanding
. We are expanding  .
.Since there are
 terms in
terms in  , there are
, there are  ways to choose one term from each
ways to choose one term from each  . The product of the selected terms is
. The product of the selected terms is  for some integer
for some integer  between
between  and
and  inclusive. For each
inclusive. For each  , there is one and only one
, there is one and only one  in
in 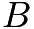 . For example, if I choose
. For example, if I choose  from
from  , then there is exactly one power of
, then there is exactly one power of  in
in  that I can choose; in this case, it would be
that I can choose; in this case, it would be  . Since there is only one way to choose one term from each
. Since there is only one way to choose one term from each  to get a product of
to get a product of  , there are
, there are  ways to choose one term from each
ways to choose one term from each  and one term from
and one term from  to get a product of
to get a product of  . Thus the coefficient of the
. Thus the coefficient of the  term is
term is  .
.Solution 2
Let
 . Then the
. Then the  term from the product in question
term from the product in question  is
is
So we are trying to find the sum of the coefficients of
 minus
minus  . Since the constant term
. Since the constant term  in
in  (when expanded) is
(when expanded) is  , and the sum of the coefficients of
, and the sum of the coefficients of  is
is  , we find the answer to be
, we find the answer to be  .
.Solution 3
We expand
 to
to  and use FOIL to multiply. It expands out to:
and use FOIL to multiply. It expands out to:


It becomes apparent that
 .
.Now we have to find the coefficient of
 in the product:
in the product: .
.We quickly see that the we get
 terms from
terms from  ,
,  ,
,  , ...
, ...  , ...
, ...  . The coefficient of
. The coefficient of  is just the sum of the coefficients of all these terms.
is just the sum of the coefficients of all these terms.  , so the answer is
, so the answer is  .
.Solution 4
Rewrite the product as
 . It is known that
. It is known that![[frac{1}{(1 - x)^n} = binom{n - 1}{n - 1} + binom{n}{n - 1}x + binom{n + 1}{n - 1}x^2 + binom{n + 2}{n - 1}x^3 + cdots + binom{n - 1 + k}{n - 1}x^k + cdots .]](https://latex.artofproblemsolving.com/d/e/c/decfea45907427e1f67cbc5124a30764644b73fc.png)
Thus, our product becomes
![[-left( x^{28} - 1 right) left( x^{15} - 1 right) left( x^{15} - 1 right) left( binom{2}{2} + binom{3}{2}x + binom{4}{2}x^2 + cdots right).]](https://latex.artofproblemsolving.com/1/8/e/18e59a7da67942850b7f55d0ae9fcee9cd482df4.png)
![[= -left( x^{28} - 1 right) left( x^{15} - 1 right) left( x^{15} - 1 right) left( 1 + 3x + 6x^2 + cdots right).]](https://latex.artofproblemsolving.com/9/1/7/9173b85d888cb0ad9d25887549b6e685ff6b083b.png)
We determine the
 coefficient by doing casework on the first three terms in our product. We can obtain an
coefficient by doing casework on the first three terms in our product. We can obtain an  term by choosing
term by choosing  in the first term,
in the first term,  in the second and third terms, and
in the second and third terms, and  in the fourth term. We can get two
in the fourth term. We can get two  terms by choosing
terms by choosing  in either the second or third term,
in either the second or third term,  in the first term,
in the first term,  in the second or third term from which
in the second or third term from which  has not been chosen, and the
has not been chosen, and the  in the fourth term. We get
in the fourth term. We get 
 terms this way. (We multiply by
terms this way. (We multiply by  because the
because the  term could have been chosen from the second term or the third term). Lastly, we can get an
term could have been chosen from the second term or the third term). Lastly, we can get an  term by choosing
term by choosing  in the first three terms and a
in the first three terms and a  from the fourth term. We have a total of
from the fourth term. We have a total of  for the
for the  coefficient, but we recall that we have a negative sign in front of our product, so we obtain an answer of
coefficient, but we recall that we have a negative sign in front of our product, so we obtain an answer of  .
. -
Solution 1
![[asy] import olympiad; size(300); defaultpen(0.8); pair C=(0,0),A=(0,3),B=(4,0),D=(4-2.28571,1.71429); pair O=incenter(A,C,D), P=incenter(B,C,D); picture p = new picture; draw(p,Circle(C,0.2)); draw(p,Circle(B,0.2)); clip(p,B--C--D--cycle); add(p); draw(A--B--C--D--C--cycle); draw(incircle(A,C,D)); draw(incircle(B,C,D)); dot(O);dot(P); label("(A)",A,W); label("(B)",B,E); label("(C)",C,W); label("(D)",D,NE); label("(O_A)",O,W); label("(O_B)",P,W); label("(3)",(A+C)/2,W); label("(4)",(B+C)/2,S); label("(frac{15}{7})",(A+D)/2,NE); label("(frac{20}{7})",(B+D)/2,NE); label("(45^{circ})",(.2,.1),E); label("(sin theta = frac{3}{5})",B-(.2,-.1),W); [/asy]](https://latex.artofproblemsolving.com/f/0/0/f003e5fe565c49bade1dc1e2b332a46d1a084ca9.png)
![[frac{BD}{4} = frac{5-BD}{3} Longrightarrow BD = frac{20}7]](https://latex.artofproblemsolving.com/9/c/9/9c9f464a5fad91f50fc120b232c9b27b70d1c93f.png) By Law of Sines on
By Law of Sines on  ,
,![[frac{BD}{sin 45^{circ}} = frac{CD}{sin angle B} Longrightarrow frac{20/7}{sqrt{2}/2} = frac{CD}{3/5} Longrightarrow CD=frac{12sqrt{2}}{7}]](https://latex.artofproblemsolving.com/9/d/f/9df704c41b92bf28dfdabff885b9a06d3fcb4441.png) Since the area of a triangle satisfies
Since the area of a triangle satisfies ![$[triangle]=rs$](https://latex.artofproblemsolving.com/6/6/d/66dc3f0f937032d1109f338a8d694db762e4ea41.png) , where
, where  the inradius and
the inradius and  the semiperimeter, we have
the semiperimeter, we have![[frac{r_A}{r_B} = frac{[ACD] cdot s_B}{[BCD] cdot s_A}]](https://latex.artofproblemsolving.com/a/f/7/af76ed60fa2fdfb3bfb69329f9c290478535c124.png) Since
Since  and
and  share the altitude (to
share the altitude (to  ), their areas are the ratio of their bases, or
), their areas are the ratio of their bases, or![[frac{[ACD]}{[BCD]} = frac{AD}{BD} = frac{3}{4}]](https://latex.artofproblemsolving.com/e/f/d/efd8576e6845c12c5b4c017aa1280a1b061fd3a6.png) The semiperimeters are
The semiperimeters are  and
and  . Thus,
. Thus,![begin{align*} frac{r_A}{r_B} &= frac{[ACD] cdot s_B}{[BCD] cdot s_A} = frac{3}{4} cdot frac{(24+ 6sqrt{2})/7}{(18+6sqrt{2})/7} \ &= frac{3(4+sqrt{2})}{4(3+sqrt{2})} cdot left(frac{3-sqrt{2}}{3-sqrt{2}}right) = frac{3}{28}(10-sqrt{2}) Rightarrow mathrm{(E)}qquad blacksquare end{align*}](https://latex.artofproblemsolving.com/b/4/3/b439f853787f7bda3a9170414daae8b3f8056e69.png)
Solution 2
![[asy] import olympiad; import geometry; size(300); defaultpen(0.8); pair C=(0,0),A=(0,3),B=(4,0),D=(4-2.28571,1.71429); pair O=incenter(A,C,D), P=incenter(B,C,D); line cd = line(C, D); picture p = new picture; picture q = new picture; picture r = new picture; picture s = new picture; draw(p,Circle(C,0.2)); clip(p,P--C--D--cycle); draw(q, Circle(C, 0.3)); clip(q, O--C--D--cycle); line l1 = perpendicular(O, cd); draw(r, l1); clip(r, C--D--O--cycle); line l2 = perpendicular(P, cd); draw(s, l2); clip(s, C--P--D--cycle); add(p); add(q); add(r); add(s); draw(A--B--C--D--C--cycle); draw(incircle(A,C,D)); draw(incircle(B,C,D)); draw(C--O); draw(C--P); dot(O); dot(P); point inter1 = intersectionpoint(l1, cd); point inter2 = intersectionpoint(l2, cd); dot(inter1); dot(inter2); label("(A)",A,W); label("(B)",B,E); label("(C)",C,W); label("(D)",D,NE); label("(O_a)",O,W); label("(O_b)",P,E); label("(3)",(A+C)/2,W); label("(4)",(B+C)/2,S); label("(frac{15}{7})",(A+D)/2,NE); label("(frac{20}{7})",(B+D)/2,NE); label("(M)", inter1, 2W); label("(N)", inter2, 2E); [/asy]](https://latex.artofproblemsolving.com/c/4/b/c4b25343784f830ea4d327aef305fb52a67bbc4a.png)
 and
and  as in solution 1. Using the angle bisector theorem, we see that
as in solution 1. Using the angle bisector theorem, we see that  and
and  . Using Stewart's Theorem gives us the equation
. Using Stewart's Theorem gives us the equation  , where
, where  is the length of
is the length of  . Solving gives us
. Solving gives us  , so
, so  .
.
Call the incenters of triangles
 and
and 
 and
and  respectively. Since
respectively. Since  is an incenter, it lies on the angle bisector of
is an incenter, it lies on the angle bisector of  . Similarly,
. Similarly,  lies on the angle bisector of
lies on the angle bisector of  . Call the point on
. Call the point on  tangent to
tangent to 
 , and the point tangent to
, and the point tangent to 
 . Since
. Since  and
and  are right, and
are right, and  ,
,  . Then,
. Then,  .
.We now use common tangents to find the length of
 and
and  . Let
. Let  , and the length of the other tangents be
, and the length of the other tangents be  and
and  . Since common tangents are equal, we can write that
. Since common tangents are equal, we can write that  ,
,  and
and  . Solving gives us that
. Solving gives us that  . Similarly,
. Similarly,  .
.We see now that

-
Solution 1
There are
 total permutations.
total permutations.For every permutation
 such that
such that  , there is exactly one permutation such that
, there is exactly one permutation such that  . Thus it suffices to count the permutations such that
. Thus it suffices to count the permutations such that  .
. ,
,  , and
, and  are the only combinations of numbers that can satisfy
are the only combinations of numbers that can satisfy  .
.There are
 combinations of numbers,
combinations of numbers,  possibilities of which side of the equation is
possibilities of which side of the equation is  and which side is
and which side is  , and
, and  possibilities for rearranging
possibilities for rearranging  and
and  . Thus, there are
. Thus, there are  permutations such that
permutations such that  .
.Thus, the number of heavy-tailed permutations is
 .
.Solution 2 (Casework)
We use case work on the value of
 .
.Case 1:
 . Since
. Since  ,
,  can only be a permutation of
can only be a permutation of  or
or  . The values of
. The values of  and
and  , as well as the values of
, as well as the values of  and
and  , are interchangeable, so this case produces a total of
, are interchangeable, so this case produces a total of  solutions.
solutions.Case 2:
 . Similarly, we have
. Similarly, we have  is a permutation of
is a permutation of  ,
,  , or
, or  , which gives a total of
, which gives a total of  solutions.
solutions.Case 3:
 .
.  is a permutation of
is a permutation of  or
or  , which gives a total of
, which gives a total of  solutions.
solutions.Case 4:
 .
.  is a permutation of
is a permutation of  ,
,  , or
, or  , which gives a total of
, which gives a total of  solutions.
solutions.Case 5:
 .
.  is a permutation of
is a permutation of  or
or  , which gives a total of
, which gives a total of  solutions.
solutions.Therefore, our answer is
 .
. -
Solution 1 (trigonometry)
Let one of the mats be
 , and the center be
, and the center be  as shown:
as shown:![[asy]unitsize(8mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=(-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle; draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); label("(x)",(-1.55,2.1),E); label("(x)",(0.03,1.5),E); label("(A)",(-3.6,2.5513),E); label("(B)",(-3.15,1.35),E); label("(C)",(0.05,3.20),E); label("(D)",(-0.75,4.15),E); label("(O)",(0.00,-0.10),E); label("(1)",(-0.1,3.8),S); label("(4)",(-0.4,2.2),S); draw((0,0)--(0,3.103)); draw((0,0)--(-2.687,1.5513)); draw((0,0)--(-0.5,3.9686));[/asy]](https://latex.artofproblemsolving.com/6/2/1/621f102520744d9e379a054f5031a004f090acff.png)
Since there are
 mats,
mats,  is equilateral. So,
is equilateral. So,  . Also,
. Also,  .
.By the Law of Cosines:
 .
.Since
 must be positive,
must be positive,  .
.Solution 2 (without trigonometry)
Draw
 and
and  as in the diagram. Draw the altitude from
as in the diagram. Draw the altitude from  to
to  and call the intersection
and call the intersection 
![[asy]unitsize(8mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=((-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle); draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); pair D = rotate(300)*(-3.687,1.5513); pair C = rotate(300)*(-2.687,1.5513); pair EE = foot((0.00,0.00),D,C); draw(D--EE--(0,0)); label("(x)",(-1.55,2.1),E); label("(x)",(0.03,1.5),E); label("(A)",(-3.6,2.5513),E); label("(B)",(-3.15,1.35),E); label("(C)",(0.05,3.20),E); label("(D)",(-0.75,4.15),E); label("(O)",(0.00,-0.10),E); label("(1)",(-0.1,3.8),S); label("(4)",(-0.4,2.2),S); draw((0,0)--(0,3.103)); draw((0,0)--(-2.687,1.5513)); draw((0,0)--(-0.5,3.9686)); label("(E)", EE,SE); [/asy]](https://latex.artofproblemsolving.com/4/6/d/46d563ae07e49e4af0f1efbe581e11a5eab9f6d8.png)
As proved in the first solution,
 . That makes
. That makes  a
a  triangle, so
triangle, so  and
and 
Since
 is a right triangle,
is a right triangle, 
Solving for
 gives
gives 
Solution 3
![[asy]unitsize(8mm); defaultpen(linewidth(.8)+fontsize(8)); draw(Circle((0,0),4)); path mat=(-2.687,-1.5513)--(-2.687,1.5513)--(-3.687,1.5513)--(-3.687,-1.5513)--cycle; draw(mat); draw(rotate(60)*mat); draw(rotate(120)*mat); draw(rotate(180)*mat); draw(rotate(240)*mat); draw(rotate(300)*mat); label("(x)",(-1.95,3),E); label("(A)",(-3.6,2.5513),E); label("(C)",(0.05,3.20),E); label("(E)",(0.40,-3.60),E); label("(B)",(-0.75,4.15),E); label("(D)",(-2.62,1.5),E); label("(F)",(-2.64,-1.43),E); label("(G)",(-0.2,-2.8),E); label("( sqrt{3}x)",(-1.5,-0.5),E); label("(M)",(-2,-0.9),E); label("(O)",(0.00,-0.10),E); label("(1)",(-2.7,2.3),S); label("(1)",(0.1,-3.4),S); label("(8)",(-0.3,0),S); draw((0,-3.103)--(-2.687,1.5513)); draw((0.5,-3.9686)--(-0.5,3.9686));[/asy]](https://latex.artofproblemsolving.com/8/4/1/841fc12191c627307cb69381b7e062642d59896d.png)
Looking at the diagram above, we know that
 is a diameter of circle
is a diameter of circle  due to symmetry. Due to Thales' theorem, triangle
due to symmetry. Due to Thales' theorem, triangle  is a right triangle with
is a right triangle with  .
.  lies on
lies on  and
and  because
because  is also a right angle. To find the length of
is also a right angle. To find the length of  , notice that if we draw a line from
, notice that if we draw a line from  to
to  , the midpoint of line
, the midpoint of line  , it creates two
, it creates two  -
-  -
-  triangles. Therefore,
triangles. Therefore,  .
. 
Use the Pythagorean theorem on triangle
 , we get
, we get![[(2+sqrt{3}x)^2 + x^2 = 8^2 Rightarrow 4 + 3x^2 + 4sqrt{3}x + x^2 = 64 Rightarrow x^2 + sqrt{3}x - 15 = 0]](https://latex.artofproblemsolving.com/e/0/b/e0b50479c5ea5d1547dba41aa7903660b135bf23.png) Using the pythagorean theorem to solve, we get
Using the pythagorean theorem to solve, we get![[x = frac{-sqrt{3} pm sqrt{3 -4(1)(-15)}}{2} = frac{pm 3sqrt{7} - sqrt{3}}{2}]](https://latex.artofproblemsolving.com/e/c/7/ec789bc2d89d3aef65c6e4f53856ba4222c1c76e.png)
 must be positive, therefore
must be positive, therefore![[x = frac{3sqrt{7} - sqrt{3}}{2} Rightarrow C]](https://latex.artofproblemsolving.com/b/7/2/b727c51e140a61adf3b44941f98e8c807b8fbb9d.png)
- Looking at the coefficients, we are immediately reminded of the binomial expansion of
 .Modifying this slightly, we can write the given equation as:
.Modifying this slightly, we can write the given equation as:![[{left(z+iright)}^{4}=1+i=2^{frac{1}{2}}cdot i cdot cos frac {pi}{4} + 2^{frac{1}{2}}cdot sin frac {pi}{4}]](https://latex.artofproblemsolving.com/e/5/7/e57d9a29e0ad784bac21443d4a88e97e7480237f.png) We can apply a translation of
We can apply a translation of  and a rotation of
and a rotation of  (both operations preserve area) to simplify the problem:
(both operations preserve area) to simplify the problem:![[z^{4}=2^{frac{1}{2}}]](https://latex.artofproblemsolving.com/7/6/9/769db790032db3f7a51b9f866767cb64a99aa2b7.png) Because the roots of this equation are created by rotating
Because the roots of this equation are created by rotating  radians successively about the origin, the quadrilateral is a square.We know that half the diagonal length of the square is
radians successively about the origin, the quadrilateral is a square.We know that half the diagonal length of the square is  Therefore, the area of the square is
Therefore, the area of the square is 
-
Solution 1
![[asy]unitsize(12mm); pair C=(0,0), B=(4 * dir(60)), A = (8,0), D=(2 * dir(60)); pair E=(1,0), F=(2,0); draw(C--B--A--C); draw(A--D);draw(D--E);draw(B--F); dot(A);dot(B);dot(C);dot(D);dot(E);dot(F); label("(C)",C,SW); label("(B)",B,N); label("(A)",A,SE); label("(D)",D,NW); label("(E)",E,S); label("(F)",F,S); label("(60^circ)",C+(.1,.1),ENE); label("(2)",1*dir(60),NW); label("(2)",3*dir(60),NW); label("(theta)",(7,.4)); label("(1)",(.5,0),S); label("(1)",(1.5,0),S); label("(x-2)",(5,0),S);[/asy]](https://latex.artofproblemsolving.com/d/d/b/ddb951a2e48a00e182fdf063f5d6ab5622700c10.png)
Let
 . Then
. Then  , and since
, and since  and
and  , we have
, we have![[tantheta = frac{frac{2sqrt{3}}{x-2} - frac{sqrt{3}}{x-1}}{1 + frac{2sqrt{3}}{x-2}cdotfrac{sqrt{3}}{x-1}}= frac{xsqrt{3}}{x^2-3x+8}]](https://latex.artofproblemsolving.com/0/e/7/0e7e40fad497d77cfc1c1273257c72565ec82619.png)
With calculus, taking the derivative and setting equal to zero will give the maximum value of
 . Otherwise, we can apply AM-GM:
. Otherwise, we can apply AM-GM:
Thus, the maximum is at
 .
.Solution 2
We notice that
 is strictly increasing on the interval
is strictly increasing on the interval  (if
(if  , then it is impossible for
, then it is impossible for  ), so we want to maximize
), so we want to maximize  .
.Consider the circumcircle of
 and let it meet
and let it meet  again at
again at  . Any point
. Any point  between
between  and
and  on line
on line  is inside this circle, so it follows that
is inside this circle, so it follows that  . Therefore to maximize
. Therefore to maximize  , the circumcircle of
, the circumcircle of  must be tangent to
must be tangent to  at
at  . By PoP we find that
. By PoP we find that  .
.Now our computations are straightforward:
![[tanangle BAD = frac{sin angle BAD}{cos angle BAD} = frac{frac{2sinangle ABD}{AD}}{frac{AB^2+AD^2-BD^2}{2ABcdot AD}}]](https://latex.artofproblemsolving.com/d/c/f/dcff624a0cc256fad91f496abb71bf1423cdbe39.png)
![[=frac{4sin angle ABDcdot AB}{AB^2+AD^2-4} = frac{4 AC sin angle ACB}{AB^2 + AD^2 - 4}]](https://latex.artofproblemsolving.com/d/a/9/da9e6eee652ee13abafd44c2c7a45fd765377a70.png)
![[=frac{4sqrt{6}}{(4^2+(2sqrt{2})^2-4cdot 2sqrt{2}) + (2^2+(2sqrt{2})^2 - 2cdot 2sqrt{2}) - 4} = frac{4sqrt{6}}{32-12sqrt{2}}]](https://latex.artofproblemsolving.com/f/f/d/ffd86fe9e02826f6e7fbc70a053486f19f91b67b.png)
![[=boxed{frac{sqrt{3}}{4sqrt{2}-3}}]](https://latex.artofproblemsolving.com/3/8/f/38ff92185ce27b5ff61a940cf18d9d32283cd288.png)
-
Solution 1
This sequence can also be expressed using matrix multiplication as follows:
![$left[ begin{array}{c} a_{n+1} \ b_{n+1} end{array} right] = left[ begin{array}{cc} sqrt{3} & -1 \ 1 & sqrt{3} end{array} right] left[ begin{array}{c} a_{n} \ b_{n} end{array} right] = 2 left[ begin{array}{cc} cos 30^circ & -sin 30^circ \ sin 30^circ & cos 30^circ end{array} right] left[ begin{array}{c} a_{n} \ b_{n} end{array} right]$](https://latex.artofproblemsolving.com/8/1/4/8145c3c2d40b98971d259f7fefb379aaf5fea0fe.png) .
.Thus,
 is formed by rotating
is formed by rotating  counter-clockwise about the origin by
counter-clockwise about the origin by  and dilating the point's position with respect to the origin by a factor of
and dilating the point's position with respect to the origin by a factor of  .
.So, starting with
 and performing the above operations
and performing the above operations  times in reverse yields
times in reverse yields  .
.Rotating
 clockwise by
clockwise by  yields
yields  . A dilation by a factor of
. A dilation by a factor of  yields the point
yields the point  .
.Therefore,
 .
.[s]Shortcut: no answer has
 in the numerator. So the point cannot have orientation
in the numerator. So the point cannot have orientation  or
or  . Also there are no negative answers. Any other non-multiple of
. Also there are no negative answers. Any other non-multiple of  rotation of
rotation of  would result in the need of radicals. So either it has orientation
would result in the need of radicals. So either it has orientation  or
or  . Both answers add up to
. Both answers add up to  . Thus,
. Thus,  .[/s] Does not work as there are negative answers.
.[/s] Does not work as there are negative answers.Solution 2 (algebra)
Let
 . Then, we can begin to list out terms as follows:
. Then, we can begin to list out terms as follows:


We notice that the sequence follows the rule

We can now start listing out every third point, getting:





We can make two observations from this:
(1) In
 , the coefficient of
, the coefficient of  and
and  is
is 
(2) The positioning of
 and
and  , and their signs, cycle with every
, and their signs, cycle with every  terms.
terms.We know then that from (1), the coefficients of
 and
and  in
in  are both
are both 
We can apply (2), finding
 , so the positions and signs of
, so the positions and signs of  and
and  are the same in
are the same in  as they are in
as they are in  .
.From this, we can get
 . We know that
. We know that  , so we get the following:
, so we get the following:

The answer is

以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









