Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2007 AMC12B 真题及答案详细解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月6日上午10:06

2007 AMC 12 B 真题

答案详细解析请参考文末

Problem 1

Isabella's house has 3 bedrooms. Each bedroom is 12 feet long, 10 feet wide, and 8 feet high. Isabella must paint the walls of all the bedrooms. Doorways and windows, which will not be painted, occupy 60 square feet in each bedroom. How many square feet of walls must be painted?

$mathrm{(A) } 678qquad mathrm{(B) } 768qquad mathrm{(C) } 786qquad mathrm{(D) } 867qquad mathrm{(E) } 876$

Problem 2

A college student drove his compact car 120 miles home for the weekend and averaged 30 miles per gallon. On the return trip the student drove his parents' SUV and averaged only 20 miles per gallon. What was the average gas mileage, in miles per gallon, for the round trip?

$mathrm {(A)} 22qquad mathrm {(B)} 24qquad mathrm {(C)} 25qquad mathrm {(D)} 26qquad mathrm {(E)} 28$

Problem 3

The point $O$ is the center of the circle circumscribed about triangle $ABC$ , with $angle BOC = 120^{circ}$ and $angle AOB = 140^{circ}$ , as shown. What is the degree measure of $angle ABC$ ?

$mathrm {(A)} 35qquad mathrm {(B)} 40qquad mathrm {(C)} 45qquad mathrm {(D)} 50qquad mathrm {(E)} 60$

Problem 4

At Frank's Fruit Market, 3 bananas cost as much as 2 apples, and 6 apples cost as much as 4 oranges. How many oranges cost as much as 18 bananas?

$mathrm {(A)} 6qquad mathrm {(B)} 8qquad mathrm {(C)} 9qquad mathrm {(D)} 12qquad mathrm {(E)} 18$

Problem 5

The 2007 AMC 12 contests will be scored by awarding 6 points for each correct response, 0 points for each incorrect response, and 1.5 points for each problem left unanswered. After looking over the 25 problems, Sarah has decided to attempt the first 22 and leave the last 3 unanswered. How many of the first 22 problems must she solve correctly in order to score at least 100 points?

$mathrm {(A)} 13qquad mathrm {(B)} 14qquad mathrm {(C)} 15qquad mathrm {(D)} 16qquad mathrm {(E)} 17$

Problem 6

Triangle $ABC$ has side lengths $AB = 5$ , $BC = 6$ , and $AC = 7$ . Two bugs start simultaneously from $A$ and crawl along the sides of the triangle in opposite directions at the same speed. They meet at point $D$ . What is $BD$ ?

$mathrm {(A)} 1qquad mathrm {(B)} 2qquad mathrm {(C)} 3qquad mathrm {(D)} 4qquad mathrm {(E)} 5$

Problem 7

All sides of the convex pentagon $ABCDE$ are of equal length, and $angle A = angle B = 90^{circ}$ . What is the degree measure of $angle E$ ?

$mathrm {(A)} 90qquad mathrm {(B)} 108qquad mathrm {(C)} 120qquad mathrm {(D)} 144qquad mathrm {(E)} 150$

Problem 8

Tom's age is $T$ years, which is also the sum of the ages of his three children. His age $N$ years ago was twice the sum of their ages then. What is $T/N$ ?

$mathrm {(A)} 2qquad mathrm {(B)} 3qquad mathrm {(C)} 4qquad mathrm {(D)} 5qquad mathrm {(E)} 6$

Problem 9

A function $f$ has the property that $f(3x-1)=x^2+x+1$ for all real numbers $x$ . What is $f(5)$ ?

$mathrm {(A)} 7qquad mathrm {(B)} 13qquad mathrm {(C)} 31qquad mathrm {(D)} 111qquad mathrm {(E)} 211$

Problem 10

Some boys and girls are having a car wash to raise money for a class trip to China. Initially $40$ % of the group are girls. Shortly thereafter two girls leave and two boys arrive, and then $30$ % of the group are girls. How many girls were initially in the group?

$mathrm {(A)} 4qquad mathrm {(B)} 6qquad mathrm {(C)} 8qquad mathrm {(D)} 10qquad mathrm {(E)} 12$

Problem 11

The angles of quadrilateral $ABCD$ satisfy $angle A=2angle B=3angle C=4angle D$ . What is the degree measure of $angle A$ , rounded to the nearest whole number?

$mathrm {(A)} 125qquad mathrm {(B)} 144qquad mathrm {(C)} 153qquad mathrm {(D)} 173qquad mathrm {(E)} 180$

Problem 12

A teacher gave a test to a class in which $10%$ of the students are juniors and $90%$ are seniors. The average score on the test was $84$ . The juniors all received the same score, and the average score of the seniors was $83$ . What score did each of the juniors receive on the test?

$mathrm {(A)} 85qquad mathrm {(B)} 88qquad mathrm {(C)} 93qquad mathrm {(D)} 94qquad mathrm {(E)} 98$

Problem 13

A traffic light runs repeatedly through the following cycle: green for $30$ seconds, then yellow for $3$ seconds, and then red for $30$ seconds. Leah picks a random three-second time interval to watch the light. What is the probability that the color changes while she is watching?

$mathrm {(A)} frac{1}{63}qquad mathrm {(B)} frac{1}{21}qquad mathrm {(C)} frac{1}{10}qquad mathrm {(D)} frac{1}{7}qquad mathrm {(E)} frac{1}{3}$

Problem 14

Point $P$ is inside equilateral $triangle ABC$ . Points $Q$ , $R$ , and $S$ are the feet of the perpendiculars from $P$ to $overline{AB}$ , $overline{BC}$ , and $overline{CA}$ , respectively. Given that $PQ=1$ , $PR=2$ , and $PS=3$ , what is $AB$ ?

$mathrm {(A)} 4qquad mathrm {(B)} 3sqrt{3}qquad mathrm {(C)} 6qquad mathrm {(D)} 4sqrt{3}qquad mathrm {(E)} 9$

Problem 15

The geometric series $a+ar+ar^2cdots$ has a sum of $7$ , and the terms involving odd powers of $r$ have a sum of $3$ . What is $a+r$ ?

$mathrm {(A)} frac{4}{3}qquad mathrm {(B)} frac{12}{7}qquad mathrm {(C)} frac{3}{2}qquad mathrm {(D)} frac{7}{3}qquad mathrm {(E)} frac{5}{2}$

Problem 16

Each face of a regular tetrahedron is painted either red, white, or blue. Two colorings are considered indistinguishable if two congruent tetrahedra with those colorings can be rotated so that their appearances are identical. How many distinguishable colorings are possible?

$mathrm {(A)} 15qquad mathrm {(B)} 18qquad mathrm {(C)} 27qquad mathrm {(D)} 54qquad mathrm {(E)} 81$

Problem 17

If $a$ is a nonzero integer and $b$ is a positive number such that $ab^2=log_{10}b$ , what is the median of the set ${0,1,a,b,1/b}$ ?

$mathrm {(A)} 0qquad mathrm {(B)} 1qquad mathrm {(C)} aqquad mathrm {(D)} bqquad mathrm {(E)} frac{1}{b}$

Problem 18

Let $a$ , $b$ , and $c$ be digits with $ane 0$ . The three-digit integer $abc$ lies one third of the way from the square of a positive integer to the square of the next larger integer. The integer $acb$ lies two thirds of the way between the same two squares. What is $a+b+c$ ?

$mathrm {(A)} 10qquad mathrm {(B)} 13qquad mathrm {(C)} 16qquad mathrm {(D)} 18qquad mathrm {(E)} 21$

Problem 19

Rhombus $ABCD$ , with side length $6$ , is rolled to form a cylinder of volume $6$ by taping $overline{AB}$ to $overline{DC}$ . What is $sin(angle ABC)$ ?

$mathrm {(A)} frac{pi}{9}qquad mathrm {(B)} frac{1}{2}qquad mathrm {(C)} frac{pi}{6}qquad mathrm {(D)} frac{pi}{4}qquad mathrm {(E)} frac{sqrt{3}}{2}$

Problem 20

The parallelogram bounded by the lines $y=ax+c$ , $y=ax+d$ , $y=bx+c$ , and $y=bx+d$ has area $18$ . The parallelogram bounded by the lines $y=ax+c$ , $y=ax-d$ , $y=bx+c$ , and $y=bx-d$ has area $72$ . Given that $a$ , $b$ , $c$ , and $d$ are positive integers, what is the smallest possible value of $a+b+c+d$ ?

$mathrm {(A)} 13qquad mathrm {(B)} 14qquad mathrm {(C)} 15qquad mathrm {(D)} 16qquad mathrm {(E)} 17$

Problem 21

The first $2007$ positive integers are each written in base $3$ . How many of these base- $3$ representations are palindromes? (A palindrome is a number that reads the same forward and backward.)

$mathrm {(A)} 100qquad mathrm {(B)} 101qquad mathrm {(C)} 102qquad mathrm {(D)} 103qquad mathrm {(E)} 104$

Problem 22

Two particles move along the edges of equilateral $triangle ABC$ in the direction $[ARightarrow BRightarrow CRightarrow A,]$ starting simultaneously and moving at the same speed. One starts at $A$ , and the other starts at the midpoint of $overline{BC}$ . The midpoint of the line segment joining the two particles traces out a path that encloses a region $R$ . What is the ratio of the area of $R$ to the area of $triangle ABC$ ?

$mathrm {(A)} frac{1}{16}qquad mathrm {(B)} frac{1}{12}qquad mathrm {(C)} frac{1}{9}qquad mathrm {(D)} frac{1}{6}qquad mathrm {(E)} frac{1}{4}$

Problem 23

How many non-congruent right triangles with positive integer leg lengths have areas that are numerically equal to $3$ times their perimeters?

$mathrm {(A)} 6qquad mathrm {(B)} 7qquad mathrm {(C)} 8qquad mathrm {(D)} 10qquad mathrm {(E)} 12$

Problem 24

How many pairs of positive integers $(a,b)$ are there such that $gcd{(a,b)}=1$ and $[frac{a}{b}+frac{14b}{9a}]$ is an integer?

$mathrm {(A)} 4qquad mathrm {(B)} 6qquad mathrm {(C)} 9qquad mathrm {(D)} 12qquad mathrm {(E)} text{infinitely many}$

Problem 25

Points $A,B,C,D$ and $E$ are located in 3-dimensional space with $AB=BC=CD=DE=EA=2$ and $angle ABC=angle CDE=angle DEA=90^o$ . The plane of $triangle ABC$ is parallel to $overline{DE}$ . What is the area of $triangle BDE$ ?

$mathrm {(A)} sqrt{2}qquad mathrm {(B)} sqrt{3}qquad mathrm {(C)} 2qquad mathrm {(D)} sqrt{5}qquad mathrm {(E)} sqrt{6}$

<hr />

2007 AMC12 B 真题答案详细解析

There are four walls in each bedroom, since she can't paint floors or ceilings. So we calculate the number of square feet of wall there is in one bedroom: $[(12*8)+(12*8)+(10*8)+(10*8)-60=160+192-60=292]$
We have three bedrooms, so she must paint
$[292*3=876 Rightarrow fbox{(E)}]$
square feet of wall.
Solution 1

The trip was $240$ miles long and took $dfrac{120}{30}+dfrac{120}{20}=4+6=10$ gallons. Therefore, the average mileage was $dfrac{240}{10}= boxed{mathrm{(B) } 24}$

Solution 2

Alternatively, we can use the harmonic mean to get $frac{2}{frac{1}{20} + frac{1}{30}} = frac{2}{frac{1}{12}} = 24$ $longrightarrow boxed{textbf{(B)} }$
$angle AOC=360-140-120=100=2angle ABC$ $angle ABC=50 Rightarrow boxed{mathrm {D}}$
18 bananas cost the same as 12 apples, and 12 apples cost the same as 8 oranges, so 18 bananas cost the same as $8 Rightarrow mathrm {(B)}$ oranges.
She must get at least $100 - 4.5 = 95.5$ points, and that can only be possible by answering at least $lceil frac{95.5}{6}rceil = 16 Rightarrow mathrm {(D)}$ questions correctly.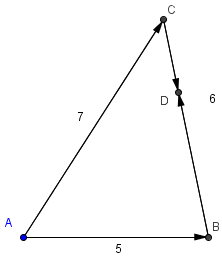
One bug goes to $B$ . The path that he takes is $dfrac{5+6+7}{2}=9$ units long. The length of $BD$ is $9-AB=9-5=4 Rightarrow mathrm {(D)}$
Since $A$ and $B$ are right angles, and $AE$ equals $BC$ , $AECB$ is a square, and $EC$ is 5. Since $ED$ and $CD$ are also 5, triangle $CDE$ is equilateral. Angle $E$ is therefore $90+60=150 Rightarrow mathrm {(E)}$
$3x-1 =5 implies x= 2$ $f(3(2)-1) = 2^2+2+1=7 implies (A)$
The traffic light runs through a $63$ second cycle.Letting $t=0$ reference the moment it turns green, the light changes at three different times: $t=30$ , $t=33$ , and $t=63$ This means that the light will change if the beginning of Leah's interval lies in $[27,30]$ , $[30,33]$ or $[60,63]$ This gives a total of $9$ seconds out of $63$ $frac{9}{63} = frac{1}{7} Rightarrow mathrm{(D)}$
Drawing , , and , is split into three smaller triangles. The altitudes of these triangles are given in the problem as , , and .Summing the areas of each of these triangles and equating it to the area of the entire triangle, we get:where is the length of a side
- Note - This is called Viviani's Theorem on Wikipedia.
Solution 1

The sum of an infinite geometric series is given by $frac{a}{1-r}$ where $a$ is the first term and $r$ is the common ratio.

In this series, $frac{a}{1-r} = 7$

The series with odd powers of $r$ is given as $[ar + ar^3 + ar^5 ...]$

It's sum can be given by $frac{ar}{1-r^2} = 3$

Doing a little algebra

$ar = 3(1-r)(1+r)$

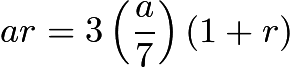
$ar = 3left(frac{a}{7}right)(1+r)$

$frac{7}{3}r = 1 + r$

$r = frac{3}{4}$

$a = 7(1-r) = frac{7}{4}$

$a + r =boxed{ frac{5}{2}} Rightarrow mathrm{(E)}$

Solution 2

The given series can be decomposed as follows: $(a + ar + ar^2 + ldots) = (a + ar^2 + ar^4 + ldots) + (ar + ar^3 + ar^5 + ldots)$

Clearly $(a + ar^2 + ar^4 + ldots) = (ar + ar^3 + ar^5 + ldots)/r = 3/r$ . We obtain that $7 = 3/r + 3$ , hence $r = frac{3}{4}$ .

Then from $7 = (a + ar + ar^2 + ldots) = frac{a}{1-r}$ we get $a=frac{7}{4}$ , and thus $a + r = frac{5}{2}$ .
A tetrahedron has 4 sides. The ratio of the number of faces with each color must be one of the following: $4:0:0$ , $3:1:0$ , $2:2:0$ , or $2:1:1$ The first ratio yields $3$ appearances, one of each color.The second ratio yields $3cdot 2 = 6$ appearances, three choices for the first color, and two choices for the second.The third ratio yields $binom{3}{2} = 3$ appearances since the two colors are interchangeable.The fourth ratio yields $3$ appearances. There are three choices for the first color, and since the second two colors are interchangeable, there is only one distinguishable pair that fits them.
The total is $3 + 6 + 3 + 3 = 15$ appearances $Rightarrow mathrm{(A)}$

Solution 2

Every colouring can be represented in the form $(w,r,b)$ , where $w$ is the number of white faces, $r$ is the number of red faces, and $b$ is the number of blue faces. Every distinguishable colouring pattern can be represented like this in exactly one way, and every ordered whole number triple with a total sum of 4 represents exactly one colouring pattern (if two tetrahedra have rearranged colours on their faces, it is always possible to rotate one so that it matches the other).

Therefore, the number of colourings is equal to the number of ways 3 distinguishable nonnegative integers can add to 4. If you have 6 cockroaches in a row, this number is equal to the number of ways to pick two of the cockroaches to eat for dinner (because the remaining cockroaches in between are separated in to three sections with a non-negative number of cockroaches each), which is $binom{6}{2} = 15$
Note that if $a$ is positive, then, the equation will have no solutions for $b$ . This becomes more obvious by noting that at $b=1$ , $ab^2 > log_{10} b$ . The LHS quadratic function will increase faster than the RHS logarithmic function, so they will never intersect.This puts $a$ as the smallest in the set since it must be negative.Checking the new equation: $-b^2 = log_{10}b$ Near $b=0$ , $-b^2 > log_{10} b$ but at $b=1$ , $-b^2 < log_{10} b$ This implies that the solution occurs somewhere in between: $0 < b < 1$ This also implies that $frac{1}{b} > 1$
This makes our set (ordered) ${a,0,b,1,1/b}$

The median is $b Rightarrow mathrm {(D)}$

Cheap Solution that most people probably used

Led $b=0.1$ . Then $acdot0.01 = -1,$ giving $a=-100$ . Then the ordered set is ${-100, 0, 0.1, 1, 10}$ and the median is $0.1=b,$ so the answer is $mathrm {(D)}$ .
The difference between $acb$ and $abc$ is given by $(100a + 10c + b) - (100a + 10b + c) = 9(c-b)$ The difference between the two squares is three times this amount or $27(c-b)$ The difference between two consecutive squares is always an odd number, therefore $c-b$ is odd. We will show that $c-b$ must be 1. Otherwise we would be looking for two consecutive squares that are at least 81 apart. But already the equation $(x+1)^2-x^2 = 27cdot 3$ solves to $x=40$ , and $40^2$ has more than three digits.The consecutive squares with common difference $27$ are $13^2=169$ and $14^2=196$ . One third of the way between them is $178$ and two thirds of the way is $187$ .
This gives $a=1$ , $b=7$ , $c=8$ .

$a+b+c = 16 Rightarrow mathrm{(C)}$
$[asy] pair B=(0,0), A=(6*dir(60)), C=(6,0); pair D=A+C; draw(A--B--C--D--A); draw(A--(3,0)); label("(A)",A,NW);label("(B)",B,SW);label("(C)",C,SE);label("(D)",D,NE); label("(6)",A/2,NW); label("(theta)",(.8,.5)); label("(h)",(3,2.6),E); [/asy]$ $V_{Cylinder} = pi r^2 h$ Where $C = 2pi r = 6$ and $h=6sintheta$ $r = frac{3}{pi}$ $V = pi left(frac{3}{pi}right)^2cdot 6sintheta$ $6 = frac{9}{pi} cdot 6sintheta$
$sintheta = frac{pi}{9} Rightarrow mathrm{(A)}$
Plotting the parallelogram on the coordinate plane, the 4 corners are at $(0,c),(0,d),left(frac{d-c}{a-b},frac{ad-bc}{a-b}right),left(frac{c-d}{a-b},frac{bc-ad}{a-b}right)$ . Because $72= 4cdot 18$ , we have that $4(c-d)left(frac{c-d}{a-b}right) = (c+d)left(frac{c+d}{a-b}right)$ or that $2(c-d)=c+d$ , which gives $c=3d$ (consider a homothety, or dilation, that carries the first parallelogram to the second parallelogram; because the area increases by $4times$ , it follows that the stretch along the diagonal, or the ratio of side lengths, is $2times$ ). The area of triangular half of the parallelogram on the right side of the y-axis is given by $9 = frac{1}{2} (c-d)left(frac{d-c}{a-b}right)$ , so substituting $c = 3d$ : $[frac{1}{2} (c-d)left(frac{c-d}{a-b}right) = 9 quad Longrightarrow quad 2d^2 = 9(a-b)]$ Thus $3|d$ , and we verify that $d = 3$ , $a-b = 2 Longrightarrow a = 3, b = 1$ will give us a minimum value for $a+b+c+d$ . Then $a+b+c+d = 3 + 1 + 9 + 3 = boxed{mathbf{(D)} 16}$ .

Solution 2

The key to this solution is that area is invariant under translation. By suitably shifting the plane, the problem is mapped to the lines $c,d,(b-a)x+c,(b-a)x+d$ and $c,-d,(b-a)x+c,(b-a)x-d$ . Now, the area of the parallelogram contained by is the former is equal to the area of a rectangle with sides $d-c$ and $frac{d-c}{b-a}$ , $frac{(d-c)^2}{b-a}=18$ , and the area contained by the latter is $frac{(c+d)^2}{b-a}=72$ . Thus, $d=3c$ and $b-a$ must be even if the former quantity is to equal $18$ . $c^2=18(b-a)$ so $c$ is a multiple of $3$ . Putting this all together, the minimal solution for $(a,b,c,d)=(3,1,3,9)$ , so the sum is $boxed{textbf{(D)} 16}$ .
$2007_{10} = 2202100_{3}$ All numbers of six or less digits in base 3 have been written.The form of each palindrome is as follows1 digit - $a$ 2 digits - $aa$ 3 digits - $aba$
4 digits - $abba$

5 digits - $abcba$

6 digits - $abccba$

Where $a,b,c$ are base 3 digits

Since $a neq 0$ , this gives a total of $2 + 2 + 2cdot 3 + 2cdot 3 + 2cdot 3^2 + 2cdot 3^2 = 52$ palindromes so far.

7 digits - $abcdcba$ , but not all of the numbers are less than $2202100_{3}$

Case: $a=1$

All of these numbers are less than $2202100_3$ giving $3^3$ more palindromes

Case: $a=2$ , $bneq 2$

All of these numbers are also small enough, giving $2cdot 3^2$ more palindromes

Case: $a=2$ , $b=2$

It follows that $c=0$ , since any other $c$ would make the value too large. This leaves the number as $220d022_3$ . Checking each value of d, all of the three are small enough, so that gives $3$ more palindromes.

Summing our cases there are $52 + 3^3 + 2cdot 3^2 + 3 = 100 Rightarrow mathrm{(A)}$
First, notice that each of the midpoints of $AB$ , $BC$ , and $CA$ are on the locus. Suppose after some time the particles have each been displaced by a short distance $x$ , to new positions $A'$ and $M'$ respectively. Consider $triangle ABM$ and drop a perpendicular from $M'$ to hit $AB$ at $Y$ . Then, $BA'=1-x$ and $BM'=1/2+x$ . From here, we can use properties of a $30-60-90$ triangle to determine the lengths $YA'$ and $YM'$ as monomials in $x$ . Thus, the locus of the midpoint will be linear between each of the three special points mentioned above. It follows that the locus consists of the only triangle with those three points as vertices. (A cheaper way to find the shape of the region is to look at the answer choices: if it were any sort of conic section then the ratio would not generally be rational.) Comparing inradii between this "midpoint" triangle and the original triangle, the area contained by $R$ must be $textbf{(A)} frac{1}{16}$ of the total area.
Let $a$ and $b$ be the two legs of the triangle.We have $frac{1}{2}ab = 3(a+b+c)$ .Then $ab=6 left(a+b+sqrt {a^2 + b^2}right)$ .We can complete the square under the root, and we get, $ab=6 left(a+b+sqrt {(a+b)^2 - 2ab}right)$ .Let $ab=p$ and $a+b=s$ , we have $p=6 left(s+ sqrt {s^2 - 2p}right)$ .After rearranging, squaring both sides, and simplifying, we have $p=12s-72$ .
Putting back $a$ and $b$ , and after factoring using $SFFT$ , we've got $(a-12)(b-12)=72$ .

Factoring 72, we get 6 pairs of $a$ and $b$

$(13, 84), (14, 48), (15, 36), (16, 30), (18, 24), (20, 21).$

And this gives us $6$ solutions $Rightarrow mathrm{(A)}$ .

Alternatively, note that $72 = 2^3 cdot 3^2$ . Then 72 has $(3+1)(2+1) = (4)(3) = 12$ factors. However, half of these are repeats, so we have $frac{12}{2} = 6$ solutions.

Solution #2

We will proceed by using the fact that $[ABC] = rcdot s$ , where $r$ is the radius of the incircle and $s$ is the semiperimeter $left(s = frac{p}{2}right)$ .

We are given $[ABC] = 3p = 6s Rightarrow rs = 6s Rightarrow r = 6$ .

The incircle of $ABC$ breaks the triangle's sides into segments such that $AB = x + y$ , $BC = x + z$ and $AC = y + z$ . Since ABC is a right triangle, one of $x$ , $y$ and $z$ is equal to its radius, 6. Let's assume $z = 6$ .

The side lengths then become $AB = x + y$ , $BC = x + 6$ and $AC = y + 6$ . Plugging into Pythagorean's theorem:

$(x + y)^2 = (x+6)^2 + (y + 6)^2$

$x^2 + 2xy + y^2 = x^2 + 12x + 36 + y^2 + 12y + 36$

$2xy - 12x - 12y = 72$

$xy - 6x - 6y = 36$

$(x - 6)(y - 6) - 36 = 36$

$(x - 6)(y - 6) = 72$

We can factor $72$ to arrive with $6$ pairs of solutions: $(7, 78), (8,42), (9, 30), (10, 24), (12, 18),$ and $(14, 15) Rightarrow mathrm{(A)}$ .
Solution 1

Combining the fraction, $frac{9a^2 + 14b^2}{9ab}$ must be an integer.

Since the denominator contains a factor of $9$ , $9 | 9a^2 + 14b^2 quadLongrightarrowquad 9 | b^2 quadLongrightarrowquad 3 | b$

Since $b = 3n$ for some positive integer $n$ , we can rewrite the fraction(divide by $9$ on both top and bottom) as $frac{a^2 + 14n^2}{3an}$

Since the denominator now contains a factor of $n$ , we get $n | a^2 + 14n^2 quadLongrightarrowquad n | a^2$ .

But since $1=gcd(a,b)=gcd(a,3n)=gcd(a,n)$ , we must have $n=1$ , and thus $b=3$ .

For $b=3$ the original fraction simplifies to $frac{a^2 + 14}{3a}$ .

For that to be an integer, $a$ must be a factor of $14$ , and therefore we must have $ain{1,2,7,14}$ . Each of these values does indeed yield an integer.

Thus there are four solutions: $(1,3)$ , $(2,3)$ , $(7,3)$ , $(14,3)$ and the answer is $mathrm{(A)}$

Solution 2

Let's assume that $frac{a}{b} + frac{14b}{9a} = m$ We get

$9a^2 - 9mab + 14b^2 = 0$

Factoring this, we get $4$ equations-

$(3a-2b)(3a-7b) = 0$

$(3a-b)(3a-14b) = 0$

$(a-2b)(9a-7b) = 0$

$(a-b)(9a-14b) = 0$

(It's all negative, because if we had positive signs, $a$ would be the opposite sign of $b$ )

Now we look at these, and see that-

$3a=2b$

$3a=b$

$3a=7b$

$3a=14b$

$a=2b$

$9a=7b$

$a=b$

$9a=14b$

This gives us $8$ solutions, but we note that the middle term needs to give you back $9m$ .

For example, in the case

$(a-2b)(9a-7b)$ , the middle term is $-25ab$ , which is not equal by $-9m$ for any integer $m$ .

Similar reason for the fourth equation. This eliminates the last four solutions out of the above eight listed, giving us 4 solutions total $mathrm {(A)}$

Solution 3

Let $u = frac{a}{b}$ . Then the given equation becomes $u + frac{14}{9u} = frac{9u^2 + 14}{9u}$ .

Let's set this equal to some value, $k Rightarrow frac{9u^2 + 14}{9u} = k$ .

Clearing the denominator and simplifying, we get a quadratic in terms of $u$ :

$9u^2 - 9ku + 14 = 0 Rightarrow u = frac{9k pm sqrt{(9k)^2 - 504}}{18}$

Since $a$ and $b$ are integers, $u$ is a rational number. This means that $sqrt{(9k)^2 - 504}$ is an integer.

Let $sqrt{(9k)^2 - 504} = x$ . Squaring and rearranging yields:

$(9k)^2 - x^2 = 504$

$(9k+x)(9k-x) = 504$ .

In order for both $x$ and $a$ to be an integer, $9k + x$ and $9k - x$ must both be odd or even. (This is easily proven using modular arithmetic.) In the case of this problem, both must be even. Let $9k + x = 2m$ and $9k - x = 2n$ .

Then:

$2m cdot 2n = 504$

$mn = 126$ .

Factoring 126, we get $6$ pairs of numbers: $(1,126), (2,63), (3,42), (6,21), (7,18),$ and $(9,14)$ .

Looking back at our equations for $m$ and $n$ , we can solve for $k = frac{2m + 2n}{18} = frac{m+n}{9}$ . Since $k$ is an integer, there are only $2$ pairs of $(m,n)$ that work: $(3,42)$ and $(6,21)$ . This means that there are $2$ values of $k$ such that $u$ is an integer. But looking back at $u$ in terms of $k$ , we have $pm$ , meaning that there are $2$ values of $u$ for every $k$ . Thus, the answer is $2 cdot 2 = 4 Rightarrow mathrm{(A)}$ .

Solution 4

Rewriting the expression over a common denominator yields $frac{9a^2 + 14b^2}{9ab}$ . This expression must be equal to some integer $m$ .

Thus, $frac{9a^2 + 14b^2}{9ab} = m rightarrow 9a^2 + 14b^2 = 9abm$ . Taking this $pmod{a}$ yields $14b^2 equiv 0pmod{a}$ . Since $gcd(a,b)=1$ , $14 equiv 0pmod{a}$ . This implies that $a|14$ so $a = 1, 2, 7, 14$ .

We can then take $9a^2 + 14b^2 = 9abm pmod{b}$ to get that $9 equiv 0 pmod{b}$ . Thus $b = 1, 3, 9$ .

However, taking $9a^2 + 14b^2 = 9abm pmod{3}$ , $b^2 equiv 0pmod{3}$ so $b$ cannot equal 1.

Also, note that if $b = 9$ , $frac{a}{b}+frac{14b}{9a} = frac{a}{9}+frac{14}{a}$ . Since $a|14$ , $frac{14}{a}$ will be an integer, but $frac{a}{9}$ will not be an integer since none of the possible values of $a$ are multiples of 9. Thus, $b$ cannot equal 9.

Thus, the only possible values of $b$ is 3, and $a$ can be 1, 2, 7, or 14. This yields 4 possible solutions, so the answer is $mathrm{(A)}$ .
Let $A=(0,0,0)$ , and $B=(2,0,0)$ . Since $EA=2$ , we could let $C=(2,0,2)$ , $D=(2,2,2)$ , and $E=(2,2,0)$ . Now to get back to $A$ we need another vertex $F=(0,2,0)$ . Now if we look at this configuration as if it was two dimensions, we would see a square missing a side if we don't draw $FA$ . Now we can bend these three sides into an equilateral triangle, and the coordinates change: $A=(0,0,0)$ , $B=(2,0,0)$ , $C=(2,0,2)$ , $D=(1,sqrt{3},2)$ , and $E=(1,sqrt{3},0)$ . Checking for all the requirements, they are all satisfied. Now we find the area of triangle $BDE$ . The side lengths of this triangle are $2, 2, 2sqrt{2}$ , which is an isosceles right triangle. Thus the area of it is $frac{2cdot2}{2}=2Rightarrow mathrm{(C)}$ .