2007 AMC12A 真题及答案详细解析
2007 AMC 12 A 真题
答案详细解析请参考文末
Problem 1
One ticket to a show costs 
at full price. Susan buys 4 tickets using a coupon that gives her a 25% discount. Pam buys 5 tickets using a coupon that gives her a 30% discount. How many more dollars does Pam pay than Susan?
Problem 2
An aquarium has a rectangular base that measures 100 cm by 40 cm and has a height of 50 cm. It is filled with water to a height of 40 cm. A brick with a rectangular base that measures 40 cm by 20 cm and a height of 10 cm is placed in the aquarium. By how many centimeters does the water rise?
Problem 3
The larger of two consecutive odd integers is three times the smaller. What is their sum?
Problem 4
Kate rode her bicycle for 30 minutes at a speed of 16 mph, then walked for 90 minutes at a speed of 4 mph. What was her overall average speed in miles per hour?
Problem 5
Last year Mr. Jon Q. Public received an inheritance. He paid 
in federal taxes on the inheritance, and paid 
of what he had left in state taxes. He paid a total of 
for both taxes. How many dollars was his inheritance?
Problem 6
Triangles 
and 
are isosceles with 
and 
. Point 
is inside triangle , angle measures 40 degrees, and angle measures 140 degrees. What is the degree measure of angle 
?
Problem 7
Let 
, and 
be five consecutive terms in an arithmetic sequence, and suppose that 
. Which of 
or can be found?
Problem 8
A star-polygon is drawn on a clock face by drawing a chord from each number to the fifth number counted clockwise from that number. That is, chords are drawn from 12 to 5, from 5 to 10, from 10 to 3, and so on, ending back at 12. What is the degree measure of the angle at each vertexin the star polygon?
Problem 9
Yan is somewhere between his home and the stadium. To get to the stadium he can walk directly to the stadium, or else he can walk home and then ride his bicycle to the stadium. He rides 7 times as fast as he walks, and both choices require the same amount of time. What is the ratioof Yan's distance from his home to his distance from the stadium?
Problem 10
A triangle with side lengths in the ratio 
is inscribed in a circle with radius 3. What is the area of the triangle?
Problem 11
A finite sequence of three-digit integers has the property that the tens and units digits of each term are, respectively, the hundreds and tens digits of the next term, and the tens and units digits of the last term are, respectively, the hundreds and tens digits of the first term. For example, such a sequence might begin with the terms 247, 475, and 756 and end with the term 824. Let 
be the sum of all the terms in the sequence. What is the largest prime factor that always divides ?
Problem 12
Integers 
and 
, not necessarily distinct, are chosen independently and at random from 0 to 2007, inclusive. What is the probability that 
is even?
Problem 13
A piece of cheese is located at 
in a coordinate plane. A mouse is at 
and is running up the line 
. At the point 
the mouse starts getting farther from the cheese rather than closer to it. What is 
?
Problem 14
Let a, b, c, d, and e be distinct integers such that
?
Problem 15
The set 
is augmented by a fifth element 
, not equal to any of the other four. The median of the resulting set is equal to its mean. What is the sum of all possible values of ?
Problem 16
How many three-digit numbers are composed of three distinct digits such that one digit is the average of the other two?
Problem 17
Suppose that 
and 
. What is 
?
Problem 18
The polynomial 
has real coefficients, and 
What is 
Problem 19
Triangles and 
have areas 
and 
respectively, with 
and 
What is the sum of all possible x-coordinates of 
?
Problem 20
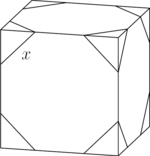
Corners are sliced off a unit cube so that the six faces each become regular octagons. What is the total volume of the removed tetrahedra?
Problem 21
The sum of the zeros, the product of the zeros, and the sum of the coefficients of the function 
are equal. Their common value must also be which of the following?
Problem 22
For each positive integer , let 
denote the sum of the digits of 
For how many values of is 
Problem 23
Square 
has area 
and 
is parallel to the x-axis. Vertices 
, and 
are on the graphs of 
and 
respectively. What is 
![$mathrm{(A)} sqrt [6]{3}qquad mathrm{(B)} sqrt {3}qquad mathrm{(C)} sqrt [3]{6}qquad mathrm{(D)} sqrt {6}qquad mathrm{(E)} 6$](https://latex.artofproblemsolving.com/b/d/1/bd13da83b605be8995acd736bd986bb7d9de5304.png)
Problem 24
For each integer 
, let 
be the number of solutions to the equation 
on the interval ![$[0,pi]$](https://latex.artofproblemsolving.com/e/c/e/ece27ba559bd93cdf2416aa0f88fc8d7d85e5791.png)
. What is 
?
Problem 25
Call a set of integers spacy if it contains no more than one out of any three consecutive integers. How many subsets of 
including the empty set, are spacy?
2007 AMC12 A 真题答案详细解析
= the amount Pam spent = the amount Susan spent
Pam pays 10 more dollars than Susan
- The brick has volume
. The base of the aquarium has area 
. For every inch the water rises, the volume increases by 
; therefore, when the volume increases by , the water level rises 
- Solution 1 Let be the smaller term. Then
- Thus, the answer is
Solution 2
- By trial and error, 1 and 3 work. 1+3=4.
- Thus, the answer is
![[16 cdot frac{30}{60}+4cdotfrac{90}{60}=14]](https://latex.artofproblemsolving.com/1/0/f/10f984f12d433181bf4e70d5aba17bf45718855a.png)
![[frac{14}2=7Rightarrowboxed{A}]](https://latex.artofproblemsolving.com/e/c/8/ec8d365a6c0eb1087db3b2f36dbfb57ab28a2d4d.png)
- After paying his taxes, he has
of his earnings left. Since 
is 
of his income, he got a total of 
. - Triangles and are isosceles with and . Point is inside triangle , angle measures 40 degrees, and angle measures 140 degrees. What is the degree measure of angle ?
- Let
be the common difference between the terms.
, so 
. But we can't find any more variables, because we don't know what is. So the answer is 
. 
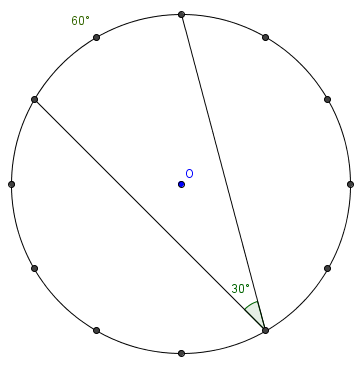We look at the angle between 12, 5, and 10. It subtends 
of the circle, or 
degrees (or you can see that the arc is 
of the right angle). Thus, the angle at each vertex is an inscribed angle subtending degrees, making the answer 
-
Solution 1
Let the distance from Yan's initial position to the stadium be
and the distance from Yan's initial position to home be 
. We are trying to find 
, and we have the following identity given by the problem:
Thus
and the answer is 
Solution 2
Another way of solving this problem is by setting the distance between Yan's home and the stadium, thus filling in one variable. Let us set the distance between the two places to be
, where 
is a random measurement (cause life, why not?) The distance to going to his home then riding his bike, which is 
times faster, is equal to him just walking to the stadium. So the equation would be: Let 
the distance from Yan's position to his home. Let 
the distance from Yan's home to the stadium.
But we're still not done with the question. We know that Yan is
from his home, and is 
or 
from the stadium. 
, the 's cancel out, and we are left with 
. Thus, the answer is ~ProGameXD
Solution 3
Assume that the distance from the home and stadium is 1, and the distance from Yan to home is
. Also assume that the speed of walking is 1, so the speed of biking is 7. Thus 
We need 
divided by 
= 
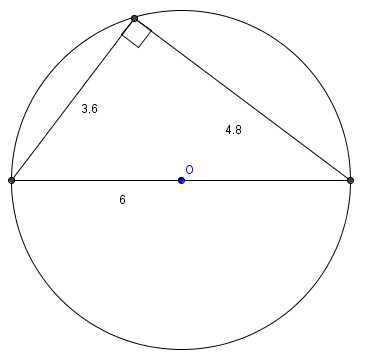Since 3-4-5 is a Pythagorean triple, the triangle is a right triangle. Since the hypotenuse is a diameter of the circumcircle, the hypotenuse is 
. Then the other legs are 
and 
. The area is 
- A given digit appears as the hundreds digit, the tens digit, and the units digit of a term the same number of times. Let
be the sum of the units digits in all the terms. Then 
, so must be divisible by 
. To see that it need not be divisible by any larger prime, the sequence 
gives 
. - The only times when is even is when
and 
are of the same parity. The chance of being odd is 
, so it has a 
probability of being even. Therefore, the probability that will be even is 
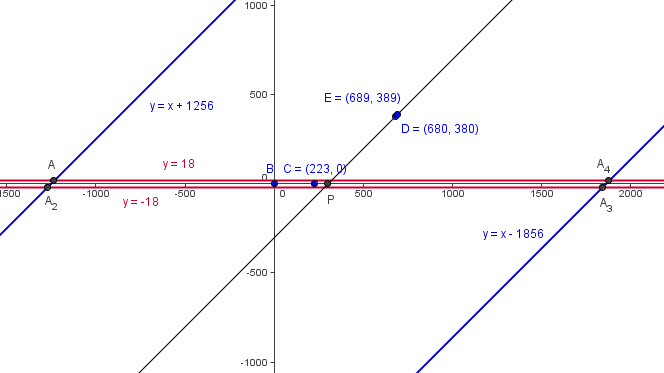
. - We are trying to find the foot of a perpendicular from to . Then the slope of the line that passes through the cheese and is the negative reciprocal of the slope of the line, or
. Therefore, the line is 
. The point where and 
intersect is 
, and 
. -
Solution 1
If 45 is expressed as a product of five distinct integer factors, the absolute value of the product of any four it as least
, so no factor can have an absolute value greater than 5. Thus the factors of the given expression are five of the integers 
. The product of all six of these is 
, so the factors are -3, -1, 1, 3, and 5. The corresponding values of a, b, c, d, and e are 9, 7, 5, 3, and 1, and their sum is 25 (C).Solution 2
The prime factorization of
is 
. Therefore, the 5 distinct integer factors must have some negative numbers in them. Because there are two 
's in the prime factorization, one of them must be negative and the other positive. Because there is a 
, there must also be a 
to cancel the negatives out. The 5 distinct integer factors must be 
. The corresponding values of and are 
. and their sum is 
- The median must either be
or . Casework:
- Median is
: Then 
and 
.
- Median is
: Then 
and 
.
- Median is : Then
and 
.
All three cases are valid, so our solution is
. - Median is
-
Solution 1
We can find the number of increasing arithmetic sequences of length 3 possible from 0 to 9, and then find all the possible permutations of these sequences.
Common difference Sequences possible Number of sequences 1 
8 2 
6 3 
4 4 
2 This gives us a total of
sequences. There are 
to permute these, for a total of 
.However, we note that the conditions of the problem require three-digit numbers, and hence our numbers cannot start with zero. There are
numbers which start with zero, so our answer is 
.Solution 2
Observe that, if the smallest and largest digit have the same parity, this uniquely determines the middle digit. If the smallest digit is not zero, then any choice of the smallest and largest digit gives
possible 3-digit numbers; otherwise, 
possible 3-digit numbers. Hence we can do simple casework on whether 0 is in the number or not.Case 1: 0 is not in the number. Then there are
ways to choose two nonzero digits of the same parity, and each choice generates 3-digit numbers, giving 
numbers.Case 2: 0 is in the number. Then there are
ways to choose the largest digit (2, 4, 6, or 8), and each choice generates 3-digit numbers, giving 
numbers.Thus the total is
.Solution 3
This solution takes advantage of the choices available, and as such, will get you nowhere on the AIME and most other contests. Observe that there's a common mistake where people forget that 0 could be part of the number. 4 valid permutations of
and 
result in 
total that they miss. Looking at the answers, only two differ by , namely and . So it's safe to bet that the answer is 
- We can make use the of the trigonometric Pythagorean identities: square both equations and add them up:
This is just the cosine difference identity, which simplifies to
-
Solution 1
A fourth degree polynomial has four roots. Since the coefficients are real(meaning that complex roots come in conjugate pairs), the remaining two roots must be the complex conjugates of the two given roots, namely
. Now we work backwards for the polynomial:
Thus our answer is
.Solution 2
Just like in Solution 1 we realize that the roots come in conjugate pairs. Which means the roots are
So our polynomial is(1)
Looking at the equation of the polynomial
. We see that 
If we plug in
into equation (1) we get 
.Now if we multiply a complex number by its conjugate we get the sum of the squares of its real and imaginary parts. Using this property on the above we multiply and get
So the answer is 
. 
Solution 1
From ![$k = [ABC] = frac 12bh$](https://latex.artofproblemsolving.com/9/a/b/9ab31a3dc0f6fe4dd1bd934c9c692a04a24c6c79.png)
, we have that the height of 
is 
. Thus lies on the lines 
.
using 45-45-90 triangles, so in 
we have that 
. The slope of 
is , so the equation of the line is 
. The point lies on one of two parallel lines that are 
units away from 
. Now take an arbitrary point on the line and draw the perpendicular to one of the parallel lines; then draw a line straight down from the same arbitrary point. These form a 45-45-90 
, so the straight line down has a length of 
. Now we note that the y-intercept of the parallel lines is either 
units above or below the y-intercept of line ; hence the equation of the parallel lines is 
.
We just need to find the intersections of these two lines and sum up the values of the x-coordinates. Substituting the 
into 
, we get 
.
Solution 2
We are finding the intersection of two pairs of parallel lines, which will form a parallelogram. The centroid of this parallelogram is just the intersection of 
and , which can easily be calculated to be 
. Now the sum of the x-coordinates is just 
.
20.
Since the sides of a regular polygon are equal in length, we can call each side 
. Examine one edge of the unit cube: each contains two slanted diagonal edges of an octagon and one straight edge. The diagonal edges form 
right triangles, making the distance on the edge of the cube 
. Thus, 
, and 
.
Each of the cut off corners is a pyramid, whose volume can be calculated by 
. Use the base as one of the three congruent isosceles triangles, with the height being one of the edges of the pyramid that sits on the edges of the cube. The height is 
. The base is a with leg of length 
, making its area 
. Plugging this in, we get that the area of one of the tetrahedra is 
. Since there are 8 removed corners, we get an answer of 
21.
By Vieta's formulas, the sum of the roots of a quadratic equation is 
, the product of the zeros is 
, and the sum of the coefficients is 
. Setting equal the first two tells us that 
. Thus, 
, so the common value is also equal to the coefficient of 
.
To disprove the others, note that:
: then 
, which is not necessarily true.
: the y-intercept is 
, so 
, not necessarily true.
: an x-intercept of the graph is a root of the polynomial, but this excludes the other root.
: the mean of the x-intercepts will be the sum of the roots of the quadratic divided by 2.
22.
Solution 1
For the sake of notation let 
. Obviously 
. Then the maximum value of 
is when 
, and the sum becomes 
. So the minimum bound is 
. We do casework upon the tens digit:
Case 1: 
. Easy to directly disprove.
Case 2: 
. 
, and 
if 
and 
otherwise.
- Subcase a:
. This exceeds our bounds, so no solution here. - Subcase b:
. First solution.
Case 3: 
. 
, and 
if 
and 
otherwise.
- Subcase a:
. Second solution. - Subcase b:
. Third solution.
Case 4: 
. But 
, and 
clearly sum to 
.
Case 5: 
. So 
and 
(recall that 
), and 
. Fourth solution.
In total we have 
solutions, which are 
and 
.
Solution 2
Clearly, 
. We can break this into three cases:
Case 1: 
- Inspection gives
.
Case 2: 
, 
(not to be confused with 
), 
- If you set up an equation, it reduces to
- which has as its only solution satisfying the constraints
, 
.
Case 3: , , 
- This reduces to
. The only two solutions satisfying the constraints for this equation are 
, 
and , 
.
The solutions are thus 
and the answer is 
.
Solution 3
As in Solution 1, we note that 
and 
.
Obviously, 
.
As 
, this means that 
, or equivalently that 
.
Thus 
. For each possible 
we get three possible .
(E. g., if 
, then 
is a number such that 
and 
, therefore 
.)
For each of these nine possibilities we compute 
as 
and check whether 
.
We'll find out that out of the 9 cases, in 4 the value has the correct sum of digits.
This happens for 
.
Solution 4
- This solution is not a good solution, but is viable for in contest situations
Clearly 
. Thus,![[n+S(n)+S(S(n))equiv 0 pmod 9 implies nequiv 0pmod 3.]](https://latex.artofproblemsolving.com/1/1/e/11ec226a9827895cfe13b288a00b8ab1d5ab6299.png)
Now we need a bound for . It is clear that the maximum for 
(from 
) which means the maximum for 
is . This means that 
.
- Warning: This is where you will cringe badly
Now check all multiples of from 
to and we find that only 
work, so our answer is .
Remark: this may seem time consuming, but in reality, calculating 
for values is actually very quick, so this solution would only take approximately 3-5 minutes, helpful in a contest.
23.
Let be the x-coordinate of and , and 
be the x-coordinate of and 
be the y-coordinate of and . Then 
and 
. Since the distance between and is , we have 
, yielding 
.
However, we can discard the negative root (all three logarithmic equations are underneath the line and above when is negative, hence we can't squeeze in a square of side 6). Thus 
.
Substituting back, 
, so ![$a = sqrt[6]{3} mathrm{(A)}$](https://latex.artofproblemsolving.com/b/3/2/b32fb7d2aa36cb5eebd4c412e5a7bed96a85daf2.png)
.
24.
Solution 1
By looking at various graphs, we obtain that, for most of the graphs
Notice that the solutions are basically reflections across 
. However, when 
, the middle apex of the sine curve touches the sine curve at the top only one time (instead of two reflected points), so we get here 
.
Solution 2
![[sin nx - sin x = 2left( cos frac {n + 1}{2}xright) left( sin frac {n - 1}{2}xright)]](https://latex.artofproblemsolving.com/8/7/1/871a5070b1c511018316319158347e8bfae88996.png)
So 
if and only if 
or 
.
The first occurs whenever 
, or 
for some nonnegative integer 
. Since 
, 
. So there are 
solutions in this case.
The second occurs whenever 
, or 
for some nonnegative integer . Here 
so that there are 
solutions here.
However, we overcount intersections. These occur whenever![[frac {2j + 1}{n + 1} = frac {2k}{n - 1}]](https://latex.artofproblemsolving.com/e/c/e/eced9caeb4854046455cc26885c31312bfde4ca2.png)
![[k = frac {(2j + 1)(n - 1)}{2(n + 1)}]](https://latex.artofproblemsolving.com/a/f/d/afdc681460be8e130fe26710fb88978f356aa940.png)
which is equivalent to 
dividing 
. If is even, then is odd, so this never happens. If 
, then there won't be intersections either, since a multiple of 8 can't divide a number which is not even a multiple of 4.
This leaves 
. In this case, the divisibility becomes 
dividing 
. Since and 
are relatively prime (subtracting twice the second number from the first gives 1), must divide 
. Since 
, 
. Then there is only one intersection, namely when 
.
Therefore we find is equal to 
, unless , in which case it is one less, or . The problem may then be finished as in Solution 1.
25.
Solution 1
Let 
denote the number of spacy subsets of 
. We have 
.
The spacy subsets of 
can be divided into two groups:
those not containing 
. Clearly 
.
those containing . We have 
, since removing from any set in produces a spacy set with all elements at most equal to 
and each such spacy set can be constructed from exactly one spacy set in .
Hence,
From this recursion, we find that
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
| 1 | 2 | 3 | 4 | 6 | 9 | 13 | 19 | 28 | 41 | 60 | 88 | 129 |
And so the answer is 
, 
.
Solution 2
Since each of the elements of the subsets must be spaced at least two apart, a divider counting argument can be used.
From the set 
we choose at most four numbers. Let those numbers be represented by balls. Between each of the balls there are at least two dividers. So for example, o | | o | | o | | o | | represents 
.
For subsets of size there must be 
dividers between the balls, leaving 
dividers to be be placed in 
spots between the balls. The number of way this can be done is 
.
Therefore, the number of spacy subsets is 
.
Solution 3
A shifting argument is also possible, and is similar in spirit to Solution 2. Clearly we can have at most elements. Given any arrangment, we subract 
from the 
element in our subset, when the elements are arranged in increasing order. This creates a bijection with the number of size subsets of the set of the first 
positive integers. For instance, the arrangment o | | o | | o | | | o | corresponds to the arrangment o o o | o |. Notice that there is no longer any restriction on consectutive numbers. Therefore, we can easily plug in the possible integers 0, 1, 2, 3, 4, 5 for : 
In general, the number of subsets of a set with elements and with no consecutive numbers is 
.
以上解析方式仅供参考
学术活动报名扫码了解！免费领取历年真题！
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
