- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2006 AMC12A 真题及答案详细解析
2006 AMC 12 A 真题
答案详细解析请参考文末
Problem 1
Sandwiches at Joe's Fast Food cost ![]() dollars each and sodas cost
dollars each and sodas cost ![]() dollars each. How many dollars will it cost to purchase
dollars each. How many dollars will it cost to purchase ![]() sandwiches and
sandwiches and ![]() sodas?
sodas?
![]()
Problem 2
Define ![]() . What is
. What is ![]() ?
?
![]()
Problem 3
The ratio of Mary's age to Alice's age is ![]() . Alice is
. Alice is ![]() years old. How old is Mary?
years old. How old is Mary?
![]()
Problem 4
A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display?
![]()
Problem 5
Doug and Dave shared a pizza with ![]() equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was
equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half the pizza. The cost of a plain pizza was ![]() dollars, and there was an additional cost of
dollars, and there was an additional cost of ![]() dollars for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug?
dollars for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each paid for what he had eaten. How many more dollars did Dave pay than Doug?
![]()
Problem 6
The ![]() rectangle
rectangle ![]() is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is
is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is ![]() ?
?![[asy] unitsize(3mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=4; draw((0,4)--(18,4)--(18,-4)--(0,-4)--cycle); draw((6,4)--(6,0)--(12,0)--(12,-4)); label("$A$",(0,4),NW); label("$B$",(18,4),NE); label("$C$",(18,-4),SE); label("$D$",(0,-4),SW); label("$y$",(3,4),S); label("$y$",(15,-4),N); label("$18$",(9,4),N); label("$18$",(9,-4),S); label("$8$",(0,0),W); label("$8$",(18,0),E); dot((0,4)); dot((18,4)); dot((18,-4)); dot((0,-4));[/asy]](https://latex.artofproblemsolving.com/6/6/a/66a524a2244d311dbe57cc4d9aaffc1b5e83bb03.png)
![]()
Problem 7
Mary is ![]() older than Sally, and Sally is
older than Sally, and Sally is ![]() younger than Danielle. The sum of their ages is
younger than Danielle. The sum of their ages is ![]() years. How old will Mary be on her next birthday?
years. How old will Mary be on her next birthday?
![]()
Problem 8
How many sets of two or more consecutive positive integers have a sum of ![]() ?
?
![]()
Problem 9
Oscar buys ![]() pencils and
pencils and ![]() erasers for
erasers for ![]() . A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser?
. A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser?
![]()
Problem 10
For how many real values of ![]() is
is ![]() an integer?
an integer?
![]()
Problem 11
Which of the following describes the graph of the equation ![]() ?
?
![]()
Problem 12
A number of linked rings, each 1 cm thick, are hanging on a peg. The top ring has an outside diameter of 20 cm. The outside diameter of each of the outer rings is 1 cm less than that of the ring above it. The bottom ring has an outside diameter of 3 cm. What is the distance, in cm, from the top of the top ring to the bottom of the bottom ring?![[asy]size(7cm); pointpen = black; pathpen = linewidth(0.7); D(CR((0,0),10)); D(CR((0,0),9.5)); D(CR((0,-18.5),9.5)); D(CR((0,-18.5),9)); MP("$vdots$",(0,-31),(0,0)); D(CR((0,-39),3)); D(CR((0,-39),2.5)); D(CR((0,-43.5),2.5)); D(CR((0,-43.5),2)); D(CR((0,-47),2)); D(CR((0,-47),1.5)); D(CR((0,-49.5),1.5)); D(CR((0,-49.5),1.0)); D((12,-10)--(12,10)); MP('20',(12,0),E); D((12,-51)--(12,-48)); MP('3',(12,-49.5),E); [/asy]](https://latex.artofproblemsolving.com/c/7/5/c7566eb2ca9233305be8873b125b5e186a871287.png)
![]()
Problem 13
The vertices of a ![]() right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?
right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?![[asy] unitsize(5mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); pair B=(0,0), C=(5,0); pair A=intersectionpoints(Circle(B,3),Circle(C,4))[0]; draw(A--B--C--cycle); draw(Circle(C,3)); draw(Circle(A,1)); draw(Circle(B,2)); label("$A$",A,N); label("$B$",B,W); label("$C$",C,E); label("3",midpoint(B--A),NW); label("4",midpoint(A--C),NE); label("5",midpoint(B--C),S);[/asy]](https://latex.artofproblemsolving.com/c/d/7/cd70a3d199aac3650e14fb5d9e5786581c4fa2ba.png)
![]()
Problem 14
Two farmers agree that pigs are worth ![]() dollars and that goats are worth
dollars and that goats are worth ![]() dollars. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a
dollars. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a ![]() dollar debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
dollar debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
![]()
Problem 15
Suppose ![]() and
and ![]() . What is the smallest possible positive value of
. What is the smallest possible positive value of ![]() ?
?
![]()
Problem 16
Circles with centers ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively. A common internal tangent intersects the circles at
, respectively. A common internal tangent intersects the circles at ![]() and
and ![]() , respectively. Lines
, respectively. Lines ![]() and
and ![]() intersect at
intersect at ![]() , and
, and ![]() . What is
. What is ![]() ?
?
![[asy]unitsize(2.5mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair A=(0,0), Ep=(5,0), B=(5+40/3,0); pair M=midpoint(A--Ep); pair C=intersectionpoints(Circle(M,2.5),Circle(A,3))[1]; pair D=B+8*dir(180+degrees(C)); dot(A); dot(C); dot(B); dot(D); draw(C--D); draw(A--B); draw(Circle(A,3)); draw(Circle(B,8)); label("$A$",A,W); label("$B$",B,E); label("$C$",C,SE); label("$E$",Ep,SSE); label("$D$",D,NW);[/asy]](https://latex.artofproblemsolving.com/b/b/4/bb4378a1b69a2fbdd9aadc5253c2e199d58719e9.png)
![]()
Problem 17
Square ![]() has side length
has side length ![]() , a circle centered at
, a circle centered at ![]() has radius
has radius ![]() , and
, and ![]() and
and ![]() are both rational. The circle passes through
are both rational. The circle passes through ![]() , and
, and ![]() lies on
lies on ![]() . Point
. Point ![]() lies on the circle, on the same side of
lies on the circle, on the same side of ![]() as
as ![]() . Segment
. Segment ![]() is tangent to the circle, and
is tangent to the circle, and ![]() . What is
. What is ![]() ?
?![[asy]unitsize(6mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=3; pair B=(0,0), C=(3,0), D=(3,3), A=(0,3); pair Ep=(3+5*sqrt(2)/6,3+5*sqrt(2)/6); pair F=intersectionpoints(Circle(A,sqrt(9+5*sqrt(2))),Circle(Ep,5/3))[0]; pair[] dots={A,B,C,D,Ep,F}; draw(A--F); draw(Circle(Ep,5/3)); draw(A--B--C--D--cycle); dot(dots); label("$A$",A,NW); label("$B$",B,SW); label("$C$",C,SE); label("$D$",D,SW); label("$E$",Ep,E); label("$F$",F,NW); [/asy]](https://latex.artofproblemsolving.com/5/0/7/5070473f4545f2932e536bc27857a5203bfe5458.png)
![]()
Problem 18
The function ![]() has the property that for each real number
has the property that for each real number ![]() in its domain,
in its domain, ![]() is also in its domain and
is also in its domain and
![]()
What is the largest set of real numbers that can be in the domain of ![]() ?
?
![]()
![]()
Problem 19
Circles with centers ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively. The equation of a common external tangent to the circles can be written in the form
, respectively. The equation of a common external tangent to the circles can be written in the form ![]() with
with ![]() . What is
. What is ![]() ?
?
![[asy]size(150); defaultpen(linewidth(0.7)+fontsize(8)); draw(circle((2,4),4));draw(circle((14,9),9)); draw((0,-2)--(0,20));draw((-6,0)--(25,0)); draw((2,4)--(2,4)+4*expi(pi*4.5/11)); draw((14,9)--(14,9)+9*expi(pi*6/7)); label("4",(2,4)+2*expi(pi*4.5/11),(-1,0)); label("9",(14,9)+4.5*expi(pi*6/7),(1,1)); label("(2,4)",(2,4),(0.5,-1.5));label("(14,9)",(14,9),(1,-1)); draw((-4,120*-4/119+912/119)--(11,120*11/119+912/119)); dot((2,4)^^(14,9));[/asy]](https://latex.artofproblemsolving.com/4/8/3/483a45d103ff0577c1129c68ae00f540094d6cd4.png)
![]()
Problem 20
A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once?
![]()
Problem 21
Let
![]()
and
![]() .
.
What is the ratio of the area of ![]() to the area of
to the area of ![]() ?
?
![]()
Problem 22
A circle of radius ![]() is concentric with and outside a regular hexagon of side length
is concentric with and outside a regular hexagon of side length ![]() . The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is
. The probability that three entire sides of hexagon are visible from a randomly chosen point on the circle is ![]() . What is
. What is ![]() ?
?
![]()
Problem 23
Given a finite sequence ![]() of
of ![]() real numbers, let
real numbers, let ![]() be the sequence
be the sequence
![]()
of ![]() real numbers. Define
real numbers. Define ![]() and, for each integer
and, for each integer ![]() ,
, ![]() , define
, define ![]() . Suppose
. Suppose ![]() , and let
, and let ![]() . If
. If ![]() , then what is
, then what is ![]() ?
?
![]()
Problem 24
The expression
![]()
is simplified by expanding it and combining like terms. How many terms are in the simplified expression?
![]()
Problem 25
How many non-empty subsets ![]() of
of ![]() have the following two properties?
have the following two properties?
![]() No two consecutive integers belong to
No two consecutive integers belong to ![]() .
.
![]() If
If ![]() contains
contains ![]() elements, then
elements, then ![]() contains no number less than
contains no number less than ![]() .
.
![]()
2006 AMC12 A 真题答案详细解析
请扫描下方二维码咨询
- The
 sandwiches cost
sandwiches cost  dollars. The
dollars. The  sodas cost
sodas cost  dollars. In total, the purchase costs
dollars. In total, the purchase costs  dollars. The answer is
dollars. The answer is  .
. - By the definition of
 , we have
, we have  . Then
. Then  . The answer is
. The answer is  .
. -
Solution 1
Let
 be Mary's age. Then
be Mary's age. Then  . Solving for
. Solving for  , we obtain
, we obtain  . The answer is
. The answer is  .
.Solution 2
We can see this is a combined ratio of
 ,
,  . We can equalize by doing
. We can equalize by doing  , and
, and  . With the common ratio of
. With the common ratio of  and difference ratio of
and difference ratio of  , we see
, we see  therefore we can see our answer is correct.
therefore we can see our answer is correct. -
Solution 1
From the greedy algorithm, we have
 in the hours section and
in the hours section and  in the minutes section.
in the minutes section. 
Solution 2
With a matrix we can see
 The largest digit sum we can see is
The largest digit sum we can see is  . For the minutes digits, we can combine the largest
. For the minutes digits, we can combine the largest  digits, which are
digits, which are  which we can then do
which we can then do 
- Dave and Doug paid
 dollars in total. Doug paid for three slices of plain pizza, which cost
dollars in total. Doug paid for three slices of plain pizza, which cost  . Dave paid
. Dave paid  dollars. Dave paid
dollars. Dave paid  more dollars than Doug. The answer is
more dollars than Doug. The answer is  .
. - Since the two hexagons are going to be repositioned to form a square without overlap, the area will remain the same. The rectangle's area is
 . This means the square will have four sides of length 12. The only way to do this is shown below.
. This means the square will have four sides of length 12. The only way to do this is shown below.![[asy] size(175); pair A,B,C,D,E,F,G,H; A=(0,8); B=(12,12); C=(12,4); D=(0,0); E=(0,12); F=(12,0); G=(6,4); H=(6,8); draw(A--E--B--C--G--H--A--D--F--C); label("$A$",A,W); label("$B$",B,NE); label("$C$",(12.6,4)); label("$D$",D,SW); label("$12$",E--B,N); label("$12$",D--F,S); label("$4$",E--A,W); label("$4$",(12.4,-1.75),E); label("$8$",A--D,W); label("$8$",(12.4,4),E); label("$y$",A--H,S); label("$y$",G--C,N); [/asy]](https://latex.artofproblemsolving.com/1/7/9/1794d4dcd643f680a8bcabca8f5ff34ed2b54a70.png) As you can see from the diagram, the line segment denoted as
As you can see from the diagram, the line segment denoted as  is half the length of the side of the square, which leads to
is half the length of the side of the square, which leads to  .
. - Let
 be Mary's age, let
be Mary's age, let  be Sally's age, and let
be Sally's age, and let  be Danielle's age. We have
be Danielle's age. We have  , and
, and  . The sum of their ages is
. The sum of their ages is  . Therefore,
. Therefore,  , and
, and  . Then
. Then  . Mary will be
. Mary will be  on her next birthday. The answer is
on her next birthday. The answer is  .
. - Notice that if the consecutive positive integers have a sum of 15, then their average (which could be a fraction) must be a divisor of 15. If the number of integers in the list is odd, then the average must be either 1, 3, or 5, and 1 is clearly not possible. The other two possibilities both work:
If the number of integers in the list is even, then the average will have a
 . The only possibility is
. The only possibility is 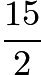 , from which we get:
, from which we get:Thus, the correct answer is 3, answer choice
 .
. - Let the price of a pencil be
 and an eraser
and an eraser  . Then
. Then  with
with  . Since
. Since  and
and  are positive integers, we must have
are positive integers, we must have  and
and  .Considering the equation
.Considering the equation  modulo 3 (that is, comparing the remainders when both sides are divided by 3) we have
modulo 3 (that is, comparing the remainders when both sides are divided by 3) we have  so
so  leaves a remainder of 1 on division by 3.Since
leaves a remainder of 1 on division by 3.Since  , possible values for
, possible values for  are 4, 7, 10 ....Since 13 pencils cost less than 100 cents,
are 4, 7, 10 ....Since 13 pencils cost less than 100 cents,  .
.  is too high, so
is too high, so  must be 4 or 7.If
must be 4 or 7.If  then
then  and so
and so  giving
giving  . This contradicts the pencil being more expensive. The only remaining value for
. This contradicts the pencil being more expensive. The only remaining value for  is 7; then the 13 pencils cost
is 7; then the 13 pencils cost  cents and so the 3 erasers together cost 9 cents and each eraser costs
cents and so the 3 erasers together cost 9 cents and each eraser costs  cents.Thus one pencil plus one eraser cost
cents.Thus one pencil plus one eraser cost  cents, which is answer choice
cents, which is answer choice  .
. - For
 to be an integer,
to be an integer,  must be a perfect square.Since
must be a perfect square.Since  can't be negative,
can't be negative,  .The perfect squares that are less than or equal to
.The perfect squares that are less than or equal to  are
are  , so there are
, so there are  values for
values for  .Since every value of
.Since every value of  gives one and only one possible value for
gives one and only one possible value for  , the number of values of
, the number of values of  is
is  .
. 
Either or
or  . The union of them is 2 lines, and thus the answer is
. The union of them is 2 lines, and thus the answer is  .
.![[asy] draw((0,-50)--(0,50));draw((-50,0)--(50,0));[/asy]](https://latex.artofproblemsolving.com/7/7/b/77bc9852606b67fe448031002c3e27a4b8a97bd1.png)
-
Solution 1
The inside diameters of the rings are the positive integers from 1 to 18. The total distance needed is the sum of these values plus 2 for the top of the first ring and the bottom of the last ring. Using the formula for the sum of an arithmetic series, the answer is
 .
.Solution 2
Alternatively, the sum of the consecutive integers from 3 to 20 is
 . However, the 17 intersections between the rings must be subtracted, and we also get
. However, the 17 intersections between the rings must be subtracted, and we also get  .
. - Let the radius of the smallest circle be
 , the radius of the second largest circle be
, the radius of the second largest circle be  , and the radius of the largest circle be
, and the radius of the largest circle be  .
.![[r_A + r_B = 3]](https://latex.artofproblemsolving.com/d/3/2/d32fc5e73b196d772754dd22491fcd35a84bb5f3.png)
![[r_A + r_C = 4]](https://latex.artofproblemsolving.com/1/9/c/19c0750788a3a435260e2fd673e16c9ac408bd4f.png)
![[r_ B + r_C = 5]](https://latex.artofproblemsolving.com/5/b/0/5b0ea74a9c0df59da5cb769e4a8d0415e3c427ea.png) Adding up all these equations and then dividing both sides by 2, we get,
Adding up all these equations and then dividing both sides by 2, we get,![[r_A + r_B + r_C = 6]](https://latex.artofproblemsolving.com/7/d/1/7d1cefc3fb4362fcd5dbae413e070ba9c5bc3a71.png) Then, we get
Then, we get  ,
,  , and
, and  Then we get
Then we get 
-
Solution 1
The problem can be restated as an equation of the form
 , where
, where  is the number of pigs,
is the number of pigs,  is the number of goats, and
is the number of goats, and  is the positive debt. The problem asks us to find the lowest x possible.
is the positive debt. The problem asks us to find the lowest x possible.  and
and  must be integers, which makes the equation a Diophantine equation. Bezout’s Identity tells us that the smallest
must be integers, which makes the equation a Diophantine equation. Bezout’s Identity tells us that the smallest  for the Diophantine equation
for the Diophantine equation  to have solutions is when
to have solutions is when  is the greatest common divisor of
is the greatest common divisor of  and
and  . Therefore, the answer is
. Therefore, the answer is  , which is
, which is  ,
, 
Solution 2
Alternatively, note that
 is divisible by 30 no matter what
is divisible by 30 no matter what  and
and  are, so our answer must be divisible by 30. In addition, three goats minus two pigs gives us
are, so our answer must be divisible by 30. In addition, three goats minus two pigs gives us  exactly. Since our theoretical best can be achieved, it must really be the best, and the answer is
exactly. Since our theoretical best can be achieved, it must really be the best, and the answer is  . debt that can be resolved.
. debt that can be resolved.Solution 3
Let us simplify this problem. Dividing by
 , we get a pig to be:
, we get a pig to be:  , and a goat to be
, and a goat to be  . It becomes evident that if you exchange
. It becomes evident that if you exchange  pigs for
pigs for  goats, we get the smallest positive difference -
goats, we get the smallest positive difference -  . Since we originally divided by
. Since we originally divided by  , we need to multiply again, thus getting the answer:
, we need to multiply again, thus getting the answer: 
- For
 , x must be in the form of
, x must be in the form of  , where
, where  denotes any integer.
denotes any integer. - For
 ,
,  .
.
- For
- The smallest possible value of
 will be that of
will be that of  .
. 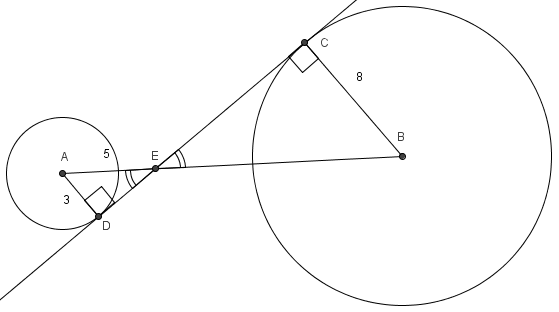
 and
and  are vertical angles so they are congruent, as are angles
are vertical angles so they are congruent, as are angles  and
and  (both are right angles because the radius and tangent line at a point on a circle are always perpendicular). Thus,
(both are right angles because the radius and tangent line at a point on a circle are always perpendicular). Thus,  . By the Pythagorean Theorem, line segment
. By the Pythagorean Theorem, line segment  . The sides are proportional, so
. The sides are proportional, so  . This makes
. This makes  and
and  .
.-
Solution 1
One possibility is to use the coordinate plane, setting
 at the origin. Point
at the origin. Point  will be
will be  and
and  will be
will be  since
since  , and
, and  are collinear and contain a diagonal of
are collinear and contain a diagonal of  . The Pythagorean theorem results in
. The Pythagorean theorem results in![[AF^2 + EF^2 = AE^2]](https://latex.artofproblemsolving.com/d/7/1/d71803837ddd2739fca2601339696a8bda7a977c.png)
![[r^2 + left(sqrt{9 + 5sqrt{2}}right)^2 = left(left(s + frac{r}{sqrt{2}}right) - 0right)^2 + left(left(s + frac{r}{sqrt{2}}right) - sright)^2]](https://latex.artofproblemsolving.com/5/f/d/5fdeb0d443078117c60e8fd7a8bc11fac819921d.png)
![[r^2 + 9 + 5sqrt{2} = s^2 + rssqrt{2} + frac{r^2}{2} + frac{r^2}{2}]](https://latex.artofproblemsolving.com/5/0/3/5035fb6846965c9f72d4bab118a4348594b3539d.png)
![[9 + 5sqrt{2} = s^2 + rssqrt{2}]](https://latex.artofproblemsolving.com/d/4/c/d4c51cc1cc2c9c1a9f1289b458925ff8757c55b9.png)
This implies that
 and
and  ; dividing gives us
; dividing gives us  .
.Solution 2
First note that angle
 is right since
is right since  is tangent to the circle. Using the Pythagorean Theorem on
is tangent to the circle. Using the Pythagorean Theorem on  , then, we see
, then, we see![[AE^2 = 9 + 5sqrt{2} + r^2.]](https://latex.artofproblemsolving.com/2/5/c/25c4083d528c34ad1d6367510a4e14faccac95f1.png)
But it can also be seen that
 . Therefore, since
. Therefore, since  lies on
lies on  ,
,  . Using the Law of Cosines on
. Using the Law of Cosines on  , we see
, we see![[AE^2 = s^2 + r^2 - 2srcos(135^circ)]](https://latex.artofproblemsolving.com/8/1/6/8161db3710ab9fa2497d6e595aa9b77859ca1577.png)
![[AE^2 = s^2 + r^2 - 2srleft(-frac{1}{sqrt{2}}right)]](https://latex.artofproblemsolving.com/e/c/a/eca29b32ce59ee360a954cac585dbdfeee4c25b9.png)
![[AE^2 = s^2 + r^2 + sqrt{2}sr]](https://latex.artofproblemsolving.com/4/0/5/40563b86e4b5862175b46ba601c2357078403ecc.png)
![[9 + 5sqrt{2} + r^2 = s^2 + r^2 + sqrt{2}sr]](https://latex.artofproblemsolving.com/9/a/b/9ab7aedd4738e7284f627b50809732dacad3f1c6.png)
![[9 + 5sqrt{2} = s^2 + sqrt{2}sr.]](https://latex.artofproblemsolving.com/c/e/b/ceb83cd257547b0822adade5376c7986adb35db7.png)
Thus, since
 and
and  are rational,
are rational,  and
and  . So
. So  ,
,  , and
, and  .
.Solution 3
(Similar to Solution 1) First, draw line AE and mark a point Z that is equidistant from E and D so that
 and that line
and that line  includes point D. Since DE is equal to the radius
includes point D. Since DE is equal to the radius  ,
, 
Note that triangles
 and
and  share the same hypotenuse
share the same hypotenuse  , meaning that
, meaning that![[AZ^2+EZ^2=AF^2+EF^2]](https://latex.artofproblemsolving.com/f/6/6/f663e70afe26fee9429f9c29f2033a144f67731b.png) Plugging in our values we have:
Plugging in our values we have:![[(s+frac{rsqrt{2}}{2})^2+(frac{rsqrt{2}}{2})^2=(sqrt{9+5sqrt{2}})^2+r^2]](https://latex.artofproblemsolving.com/b/9/a/b9a65652c1aafc775a78f65420d00204260e7ea4.png)
![[s^2+srsqrt{2}+frac{r^2}{2}+frac{r^2}{2}=9+5sqrt{2}+r^2]](https://latex.artofproblemsolving.com/e/f/5/ef5e6ee171a750a306c118b67f27c3cf96e32dda.png)
![[s^2+srsqrt{2}=9+5sqrt{2}]](https://latex.artofproblemsolving.com/5/6/4/5640b3c27003030cc9bc0dd605220ee494b14993.png) By logic
By logic  and
and 
Therefore,

- Quickly verifying by plugging in values verifies that
 and
and  are in the domain.
are in the domain. Plugging in
Plugging in  into the function:
into the function:
 Since
Since  cannot have two values:
cannot have two values:


Therefore, the largest set of real numbers that can be in the domain of
 is
is 
- Let
 be the line that goes through
be the line that goes through  and
and  , and let
, and let  be the line
be the line  . If we let
. If we let  be the measure of the acute angle formed by
be the measure of the acute angle formed by  and the x-axis, then
and the x-axis, then  .
.  clearly bisects the angle formed by
clearly bisects the angle formed by  and the x-axis, so
and the x-axis, so  . We also know that
. We also know that  and
and  intersect at a point on the x-axis. The equation of
intersect at a point on the x-axis. The equation of  is
is  , so the coordinate of this point is
, so the coordinate of this point is  . Hence the equation of
. Hence the equation of  is
is  , so
, so  , and our answer choice is
, and our answer choice is  .
. -
Solution 1
![[asy] import three; unitsize(1cm); size(50); currentprojection=orthographic(1/2,-1,1/2); /* three - currentprojection, orthographic */ draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle); draw((0,0,0)--(0,0,1)); draw((0,1,0)--(0,1,1)); draw((1,1,0)--(1,1,1)); draw((1,0,0)--(1,0,1)); draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle); [/asy]](https://latex.artofproblemsolving.com/0/c/3/0c387d5337e7fcb06d2997018524c80f0caef086.png)
Let us count the good paths. The bug starts at an arbitrary vertex, moves to a neighboring vertex (3 ways), and then to a new neighbor (2 more ways). So, without loss of generality, let the cube have vertices
 such that
such that  and
and  are two opposite faces with
are two opposite faces with  above
above  and
and  above
above  . The bug starts at
. The bug starts at  and moves first to
and moves first to  , then to
, then to  .
.From this point, there are two cases.
Case 1: the bug moves to
 . From
. From  , there is only one good move available, to
, there is only one good move available, to  . From
. From  , there are two ways to finish the trip, either by going
, there are two ways to finish the trip, either by going  or
or  . So there are 2 good paths in this case.
. So there are 2 good paths in this case.Case 2: the bug moves to
 . Case 2a: the bug moves
. Case 2a: the bug moves  . In this case, there are 0 good paths because it will not be possible to visit both
. In this case, there are 0 good paths because it will not be possible to visit both  and
and  without double-visiting some vertex. Case 2b: the bug moves
without double-visiting some vertex. Case 2b: the bug moves  . There is a unique good path in this case,
. There is a unique good path in this case,  .
.Thus, all told we have 3 good paths after the first two mo, for a total of
 good paths. There were
good paths. There were  possible paths the bug could have taken, so the probability a random path is good is the ratio of good paths to total paths,
possible paths the bug could have taken, so the probability a random path is good is the ratio of good paths to total paths,  .
.Solution 2 (using the answer choices)
As in Solution 1, the bug can move from its arbitrary starting vertex to a neighboring vertex in 3 ways. After this, the bug can move to a new neighbor in 2 ways (it cannot return to the first vertex). The total number of paths (as stated above) is
 or
or  . Therefore, the probability of the bug following a good path is equal to
. Therefore, the probability of the bug following a good path is equal to  for some positive integer
for some positive integer  . The only answer choice which can be expressed in this form is
. The only answer choice which can be expressed in this form is  .
. - Looking at the constraints of
 :
:






 is a circle with a radius of
is a circle with a radius of  . So, the area of
. So, the area of  is
is  .
.Looking at the constraints of
 :
:






 is a circle with a radius of
is a circle with a radius of  . So, the area of
. So, the area of  is
is  .
.So the desired ratio is
 .
. - Project any two non-adjacent and non-opposite sides of the hexagon to the circle; the arc between the two points formed is the location where all three sides of the hexagon can be fully viewed. Since there are six such pairs of sides, there are six arcs. The probability of choosing a point is
 , or if the total arc degree measures add up to
, or if the total arc degree measures add up to  . Each arc must equal
. Each arc must equal  .
.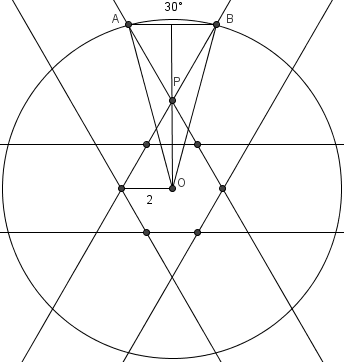 Call the center
Call the center  , and the two endpoints of the arc
, and the two endpoints of the arc  and
and  , so
, so  . Let
. Let  be the intersections of the projections of the sides of the hexagon corresponding to
be the intersections of the projections of the sides of the hexagon corresponding to  . Notice that
. Notice that  is an isosceles triangle:
is an isosceles triangle:  and
and  . Since
. Since  is a radius and
is a radius and  can be found in terms of a side of the hexagon, we are almost done.If we draw the altitude of
can be found in terms of a side of the hexagon, we are almost done.If we draw the altitude of  from
from  , then we get a right triangle. Using simple trigonometry,
, then we get a right triangle. Using simple trigonometry,  .Since
.Since  , we get
, we get  .
. 

 In general,
In general,  such that
such that  has
has  terms. Specifically,
terms. Specifically,  To find x, we need only solve the equation
To find x, we need only solve the equation  . Algebra yields
. Algebra yields  .
.-
Solution 1
By the Multinomial Theorem, the summands can be written as
![[sum_{a+b+c=2006}{frac{2006!}{a!b!c!}x^ay^bz^c}]](https://latex.artofproblemsolving.com/7/b/7/7b78526602fd2bf277218a45fd8d1fdcc3efcdf4.png)
and
![[sum_{a+b+c=2006}{frac{2006!}{a!b!c!}x^a(-y)^b(-z)^c},]](https://latex.artofproblemsolving.com/1/3/5/1353e7455d59a32ac3de47ace211b252a9bd0cf6.png)
respectively. Since the coefficients of like terms are the same in each expression, each like term either cancel one another out or the coefficient doubles. In each expansion there are:
![[{2006+2choose 2} = 2015028]](https://latex.artofproblemsolving.com/8/d/3/8d3ff6f9a5045933c1619fcab5e8bd4a48ee0457.png)
terms without cancellation. For any term in the second expansion to be negative, the parity of the exponents of
 and
and  must be opposite. Now we find a pattern:
must be opposite. Now we find a pattern:if the exponent of
 is 1, the exponent of
is 1, the exponent of  can be all even integers up to 2004, so there are 1003 terms.
can be all even integers up to 2004, so there are 1003 terms.if the exponent of
 is 3, the exponent of
is 3, the exponent of  can go up to 2002, so there are 1002 terms.
can go up to 2002, so there are 1002 terms.
if the exponent of
 is 2005, then
is 2005, then  can only be 0, so there is 1 term.
can only be 0, so there is 1 term.If we add them up, we get
 terms. However, we can switch the exponents of
terms. However, we can switch the exponents of  and
and  and these terms will still have a negative sign. So there are a total of
and these terms will still have a negative sign. So there are a total of  negative terms.
negative terms.By subtracting this number from 2015028, we obtain
 or
or  as our answer.
as our answer.Solution 2
Alternatively, we can use a generating function to solve this problem. The goal is to find the generating function for the number of unique terms in the simplified expression (in terms of
 ). In other words, we want to find
). In other words, we want to find  where the coefficient of
where the coefficient of  equals the number of unique terms in
equals the number of unique terms in  .
.First, we note that all unique terms in the expression have the form,
 , where
, where  and
and  is some constant. Therefore, the generating function for the MAXIMUM number of unique terms possible in the simplified expression of
is some constant. Therefore, the generating function for the MAXIMUM number of unique terms possible in the simplified expression of  is
is![[(1+x+x^2+x^3cdots)^3 = frac{1}{(1-x)^3}]](https://latex.artofproblemsolving.com/8/4/c/84c7d0006cfd2e05e461469355b98a403024b42c.png)
Secondly, we note that a certain number of terms of the form,
 , do not appear in the simplified version of our expression because those terms cancel. Specifically, we observe that terms cancel when
, do not appear in the simplified version of our expression because those terms cancel. Specifically, we observe that terms cancel when  because every unique term is of the form:
because every unique term is of the form:![[binom{k}{a,b,c}x^ay^bz^c+(-1)^{b+c}binom{k}{a,b,c}x^ay^bz^c]](https://latex.artofproblemsolving.com/4/3/9/439e76ff20585a54ea8ac17bcc0f8263e4c81b56.png) for all possible
for all possible  .
.Since the generating function for the maximum number of unique terms is already known, it is logical that we want to find the generating function for the number of terms that cancel, also in terms of
 . With some thought, we see that this desired generating function is the following:
. With some thought, we see that this desired generating function is the following:![[2(x+x^3+x^5cdots)(1+x^2+x^4cdots)(1+x+x^2+x^3cdots) = frac{2x}{(1-x)^3(1+x)^2}]](https://latex.artofproblemsolving.com/e/e/6/ee6d5ceef465fdd6d7a1cb47f3c8363ae8b28f26.png)
Now, we want to subtract the latter from the former in order to get the generating function for the number of unique terms in
 , our initial goal:
, our initial goal:![[frac{1}{(1-x)^3}-frac{2x}{(1-x)^3(1+x)^2} = frac{x^2+1}{(1-x)^3(1+x)^2}]](https://latex.artofproblemsolving.com/9/1/b/91b72d34758e7ed145a1c511bd2723978d2439a4.png) which equals
which equals![[(x^2+1)(1+x+x^2cdots)^3(1-x+x^2-x^3cdots)^2]](https://latex.artofproblemsolving.com/3/0/f/30f0bb48c16a88abe79887795d4c9a4cb7a2724c.png)
The coefficient of
 of the above expression equals
of the above expression equals![[sum_{a=0}^{2006}binom{2+a}{2}binom{1+2006-a}{1}(-1)^a + sum_{a=0}^{2004}binom{2+a}{2}binom{1+2004-a}{1}(-1)^a]](https://latex.artofproblemsolving.com/6/5/6/656d32098986fa900dc1f04828eb37888180a9bc.png)
Evaluating the expression, we get
 , as expected.
, as expected.Solution 3
Define
 such that
such that  . Then the expression in the problem becomes:
. Then the expression in the problem becomes:  .
.Expanding this using binomial theorem gives
 , where
, where  (we may omit the coefficients, as we are seeking for the number of terms, not the terms themselves).
(we may omit the coefficients, as we are seeking for the number of terms, not the terms themselves).Simplifying gives:
 . Note that two terms that come out of different powers of
. Note that two terms that come out of different powers of  cannot combine and simplify, as their exponent of
cannot combine and simplify, as their exponent of  will differ. Therefore, we simply add the number of terms produced from each addend. By the Binomial Theorem,
will differ. Therefore, we simply add the number of terms produced from each addend. By the Binomial Theorem,  will have
will have  terms, so the answer is
terms, so the answer is  .
.Solution 4
Using stars and bars we know that
 has
has  or
or  different terms. Now we need to find out how many of these terms are canceled out by
different terms. Now we need to find out how many of these terms are canceled out by  . We know that for any term(let's say
. We know that for any term(let's say  ) where
) where  of the expansion of
of the expansion of is only going to cancel out with the corresponding term
is only going to cancel out with the corresponding term  if only
if only  is odd and
is odd and  is even or
is even or  is even and
is even and  is odd. Now let's do some casework to see how many terms fit this criteria:
is odd. Now let's do some casework to see how many terms fit this criteria:Case 1:
 is even
is evenNow we know that
 is even and
is even and  . Thus
. Thus  is also even or both
is also even or both  and
and  are odd or both
are odd or both  and
and  are even. This case clearly fails the above criteria and there are 0 possible solutions.
are even. This case clearly fails the above criteria and there are 0 possible solutions.Case 2:
 is odd
is oddNow we know that
 is odd and
is odd and  . Thus
. Thus  is odd and
is odd and  is odd and
is odd and  is even or
is even or  is even and
is even and  is odd. All terms that have
is odd. All terms that have  being odd work.
being odd work.We now need to figure out how many of the terms have
 as a odd number. We know that
as a odd number. We know that  can be equal to any number between 0 and 2006. There are 1003 odd numbers between this range and 2007 total numbers. Thus
can be equal to any number between 0 and 2006. There are 1003 odd numbers between this range and 2007 total numbers. Thus  of the
of the  terms will cancel out and
terms will cancel out and  of the terms will work. Thus there are
of the terms will work. Thus there are  terms. This number comes out to be
terms. This number comes out to be 
 (Author: David Camacho)
(Author: David Camacho) -
Solution 1
This question can be solved fairly directly by casework and pattern-finding. We give a somewhat more general attack, based on the solution to the following problem:
How many ways are there to choose
 elements from an ordered
elements from an ordered  element set without choosing two consecutive members?
element set without choosing two consecutive members?You want to choose
 numbers out of
numbers out of  with no consecutive numbers. For each configuration, we can subtract
with no consecutive numbers. For each configuration, we can subtract  from the
from the  -th element in your subset. This converts your configuration into a configuration with
-th element in your subset. This converts your configuration into a configuration with  elements where the largest possible element is
elements where the largest possible element is  , with no restriction on consecutive numbers. Since this process is easily reversible, we have a bijection. Without consideration of the second condition, we have:
, with no restriction on consecutive numbers. Since this process is easily reversible, we have a bijection. Without consideration of the second condition, we have: 
Now we examine the second condition. It simply states that no element in our original configuration (and hence also the modified configuration, since we don't move the smallest element) can be less than
 , which translates to subtracting
, which translates to subtracting  from the "top" of each binomial coefficient. Now we have, after we cancel all the terms
from the "top" of each binomial coefficient. Now we have, after we cancel all the terms  where
where  ,
,
Solution 2
Another way of visualizing the solution above would be to use
 's and
's and  's. Denote
's. Denote  as the numbers we have chosen and
as the numbers we have chosen and  as other numbers. Taking an example, assuming we are picking two numbers, we imagine the shape
as other numbers. Taking an example, assuming we are picking two numbers, we imagine the shape  . This notation forces a number between the two chosen numbers, which blocks the two numbers we picked from being consecutive. Now we consider the orientations with this shape. We have
. This notation forces a number between the two chosen numbers, which blocks the two numbers we picked from being consecutive. Now we consider the orientations with this shape. We have  remaining numbers.
remaining numbers.We need to find the number of ways to place the remaining
 's. We can find this by utilizing stars and bars, with the following marker being placed to represent groups: *| - *|*. Now, we have to place
's. We can find this by utilizing stars and bars, with the following marker being placed to represent groups: *| - *|*. Now, we have to place  numbers within
numbers within  groups, which is
groups, which is  . The same concept can be used for the remaining numbers. The rest of the solution continues as above.
. The same concept can be used for the remaining numbers. The rest of the solution continues as above.Solution by: Everyoneintexas
Solution 3
We have the same setup as in the previous solution.
Note that if
 , the answer will be 0. Otherwise, the
, the answer will be 0. Otherwise, the  elements we choose define
elements we choose define  boxes (which divide the nonconsecutive numbers) into which we can drop the
boxes (which divide the nonconsecutive numbers) into which we can drop the  remaining elements, with the caveat that each of the middle
remaining elements, with the caveat that each of the middle  boxes must have at least one element (since the numbers are nonconsecutive). This is equivalent to dropping
boxes must have at least one element (since the numbers are nonconsecutive). This is equivalent to dropping  elements into
elements into  boxes, where each box is allowed to be empty. And this is equivalent to arranging
boxes, where each box is allowed to be empty. And this is equivalent to arranging  objects,
objects,  of which are dividers, which we can do in
of which are dividers, which we can do in  ways.
ways.Now, looking at our original question, we see that the thing we want to calculate is just

以上解析方式仅供参考

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









