Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2005 AMC12A 真题及答案详细解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月5日下午5:26

2005 AMC 12 A 真题

真题及解析

Problem 1

Two is $10 %$ of $x$ and $20 %$ of $y$ . What is $x - y$ ?

$(mathrm {A}) 1 qquad (mathrm {B}) 2 qquad (mathrm {C}) 5 qquad (mathrm {D}) 10 qquad (mathrm {E}) 20$

Problem 2

The equations $2x + 7 = 3$ and $bx - 10 = - 2$ have the same solution. What is the value of $b$ ?

$(mathrm {A}) -8 qquad (mathrm {B}) -4 qquad (mathrm {C}) 2 qquad (mathrm {D}) 4 qquad (mathrm {E}) 8$

Problem 3

A rectangle with diagonal length $x$ is twice as long as it is wide. What is the area of the rectangle?

$(mathrm {A}) frac 14x^2 qquad (mathrm {B}) frac 25x^2 qquad (mathrm {C}) frac 12x^2 qquad (mathrm {D}) x^2 qquad (mathrm {E}) frac 32x^2$

Problem 4

A store normally sells windows at $$100$ each. This week the store is offering one free window for each purchase of four. Dave needs seven windows and Doug needs eight windows. How much will they save if they purchase the windows together rather than separately?

$(mathrm {A}) 100 qquad (mathrm {B}) 200 qquad (mathrm {C}) 300 qquad (mathrm {D}) 400 qquad (mathrm {E}) 500$

Problem 5

The average (mean) of 20 numbers is 30, and the average of 30 other numbers is 20. What is the average of all 50 numbers?

$(mathrm {A}) 23 qquad (mathrm {B}) 24 qquad (mathrm {C}) 25 qquad (mathrm {D}) 26 qquad (mathrm {E}) 27$

Problem 6

Josh and Mike live 13 miles apart. Yesterday, Josh started to ride his bicycle toward Mike's house. A little later Mike started to ride his bicycle toward Josh's house. When they met, Josh had ridden for twice the length of time as Mike and at four-fifths of Mike's rate. How many miles had Mike ridden when they met?

$(mathrm {A}) 4 qquad (mathrm {B}) 5 qquad (mathrm {C}) 6 qquad (mathrm {D}) 7 qquad (mathrm {E}) 8$

Problem 7

Square $EFGH$ is inside the square $ABCD$ so that each side of $EFGH$ can be extended to pass through a vertex of $ABCD$ . Square $ABCD$ has side length $sqrt {50}$ and $BE = 1$ . What is the area of the inner square $EFGH$ ? $[asy] unitsize(4cm); defaultpen(linewidth(.8pt)+fontsize(10pt)); pair D=(0,0), C=(1,0), B=(1,1), A=(0,1); pair F=intersectionpoints(Circle(D,2/sqrt(5)),Circle(A,1))[0]; pair G=foot(A,D,F), H=foot(B,A,G), E=foot(C,B,H); draw(A--B--C--D--cycle); draw(D--F); draw(C--E); draw(B--H); draw(A--G); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,SE); label("$D$",D,SW); label("$E$",E,NNW); label("$F$",F,ENE); label("$G$",G,SSE); label("$H$",H,WSW);[/asy]$

$(mathrm {A}) 25 qquad (mathrm {B}) 32 qquad (mathrm {C}) 36 qquad (mathrm {D}) 40 qquad (mathrm {E}) 42$

Problem 8

Let $A,M$ , and $C$ be digits with

$[(100A+10M+C)(A+M+C) = 2005]$

What is $A$ ?

$(mathrm {A}) 1 qquad (mathrm {B}) 2 qquad (mathrm {C}) 3 qquad (mathrm {D}) 4 qquad (mathrm {E}) 5$

Problem 9

There are two values of $a$ for which the equation $4x^2 + ax + 8x + 9 = 0$ has only one solution for $x$ . What is the sum of these values of $a$ ?

$(mathrm {A}) -16 qquad (mathrm {B}) -8 qquad (mathrm {C}) 0 qquad (mathrm {D}) 8 qquad (mathrm {E}) 20$

Problem 10

A wooden cube $n$ units on a side is painted red on all six faces and then cut into $n^3$ unit cubes. Exactly one-fourth of the total number of faces of the unit cubes are red. What is $n$ ?

$(mathrm {A}) 3 qquad (mathrm {B}) 4 qquad (mathrm {C}) 5 qquad (mathrm {D}) 6 qquad (mathrm {E}) 7$

Problem 11

How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?

$(mathrm {A}) 41 qquad (mathrm {B}) 42 qquad (mathrm {C}) 43 qquad (mathrm {D}) 44 qquad (mathrm {E}) 45$

Problem 12

A line passes through $A (1,1)$ and $B (100,1000)$ . How many other points with integer coordinates are on the line and strictly between $A$ and $B$ ?

$(mathrm {A}) 0 qquad (mathrm {B}) 2 qquad (mathrm {C}) 3 qquad (mathrm {D}) 8 qquad (mathrm {E}) 9$

Problem 13

In the five-sided star shown, the letters $A$ , $B$ , $C$ , $D$ and $E$ are replaced by the numbers 3, 5, 6, 7 and 9, although not necessarily in that order. The sums of the numbers at the ends of the line segments $overline{AB}$ , $overline{BC}$ , $overline{CD}$ , $overline{DE}$ , and $overline{EA}$ form an arithmetic sequence, although not necessarily in that order. What is the middle term of the arithmetic sequence?

$[asy] draw((0,0)--(0.5,1.54)--(1,0)--(-0.31,0.95)--(1.31,0.95)--cycle); label("$A$",(0.5,1.54),N); label("$B$",(1,0),SE); label("$C$",(-0.31,0.95),W); label("$D$",(1.31,0.95),E); label("$E$",(0,0),SW); [/asy]$

$(mathrm {A}) 9 qquad (mathrm {B}) 10 qquad (mathrm {C}) 11 qquad (mathrm {D}) 12 qquad (mathrm {E}) 13$

Problem 14

On a standard die one of the dots is removed at random with each dot equally likely to be chosen. The die is then rolled. What is the probability that the top face has an odd number of dots?

$(mathrm {A}) frac{5}{11} qquad (mathrm {B}) frac{10}{21} qquad (mathrm {C}) frac{1}{2} qquad (mathrm {D}) frac{11}{21} qquad (mathrm {E}) frac{6}{11}$

Problem 15

Let $overline{AB}$ be a diameter of a circle and $C$ be a point on $overline{AB}$ with $2 cdot AC = BC$ . Let $D$ and $E$ be points on the circle such that $overline{DC} perp overline{AB}$ and $overline{DE}$ is a second diameter. What is the ratio of the area of $triangle DCE$ to the area of $triangle ABD$ ?

$[asy] unitsize(2.5cm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0), C=(-1/3.0), B=(1,0), A=(-1,0); pair D=dir(aCos(C.x)), E=(-D.x,-D.y); draw(A--B--D--cycle); draw(D--E--C); draw(unitcircle,white); drawline(D,C); dot(O); clip(unitcircle); draw(unitcircle); label("$E$",E,SSE); label("$B$",B,E); label("$A$",A,W); label("$D$",D,NNW); label("$C$",C,SW); draw(rightanglemark(D,C,B,2));[/asy]$

$(text {A}) frac {1}{6} qquad (text {B}) frac {1}{4} qquad (text {C}) frac {1}{3} qquad (text {D}) frac {1}{2} qquad (text {E}) frac {2}{3}$

Problem 16

Three circles of radius $s$ are drawn in the first quadrant of the $xy$ -plane. The first circle is tangent to both axes, the second is tangent to the first circle and the $x$ -axis, and the third is tangent to the first circle and the $y$ -axis. A circle of radius $r > s$ is tangent to both axes and to the second and third circles. What is $r/s$ ?

$[asy] import graph; unitsize(3mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=3; pair O0=(9,9), O1=(1,1), O2=(3,1), O3=(1,3); pair P0=O0+9*dir(-45), P3=O3+dir(70); pair[] ps={O0,O1,O2,O3}; dot(ps); draw(Circle(O0,9)); draw(Circle(O1,1)); draw(Circle(O2,1)); draw(Circle(O3,1)); draw(O0--P0,linetype("3 3")); draw(O3--P3,linetype("2 2")); draw((0,0)--(18,0)); draw((0,0)--(0,18)); label("$r$",midpoint(O0--P0),NE); label("$s$",(-1.5,4)); draw((-1,4)--midpoint(O3--P3));[/asy]$

$(mathrm {A}) 5 qquad (mathrm {B}) 6 qquad (mathrm {C}) 8 qquad (mathrm {D}) 9 qquad (mathrm {E}) 10$

Problem 17

A unit cube is cut twice to form three triangular prisms, two of which are congruent, as shown in Figure 1. The cube is then cut in the same manner along the dashed lines shown in Figure 2. This creates nine pieces. What is the volume of the piece that contains vertex $W$ ?

$(mathrm {A}) frac {1}{12} qquad (mathrm {B}) frac {1}{9} qquad (mathrm {C}) frac {1}{8} qquad (mathrm {D}) frac {1}{6} qquad (mathrm {E}) frac {1}{4}$

Problem 18

Call a number "prime-looking" if it is composite but not divisible by 2, 3, or 5. The three smallest prime-looking numbers are 49, 77, and 91. There are 168 prime numbers less than 1000. How many prime-looking numbers are there less than 1000?

$(mathrm {A}) 100 qquad (mathrm {B}) 102 qquad (mathrm {C}) 104 qquad (mathrm {D}) 106 qquad (mathrm {E}) 108$

Problem 19

A faulty car odometer proceeds from digit 3 to digit 5, always skipping the digit 4, regardless of position. If the odometer now reads 002005, how many miles has the car actually traveled?

$(mathrm {A}) 1404 qquad (mathrm {B}) 1462 qquad (mathrm {C}) 1604 qquad (mathrm {D}) 1605 qquad (mathrm {E}) 1804$

Problem 20

For each $x$ in $[0,1]$ , define

$begin{cases} f(x) = 2x, qquadqquad mathrm{if} quad 0 leq x leq frac{1}{2};\ f(x) = 2-2x, qquad mathrm{if} quad frac{1}{2} < x leq 1. end{cases}$

Let $f^{[2]}(x) = f(f(x))$ , and $f^{[n + 1]}(x) = f^{[n]}(f(x))$ for each integer $n geq 2$ . For how many values of $x$ in $[0,1]$ is $f^{[2005]}(x) = frac {1}{2}$ ?

$(mathrm {A}) 0 qquad (mathrm {B}) 2005 qquad (mathrm {C}) 4010 qquad (mathrm {D}) 2005^2 qquad (mathrm {E}) 2^{2005}$

Problem 21

How many ordered triples of integers $(a,b,c)$ , with $a ge 2$ , $bge 1$ , and $c ge 0$ , satisfy both $log_a b = c^{2005}$ and $a + b + c = 2005$ ?

$mathrm{(A)} 0 qquad mathrm{(B)} 1 qquad mathrm{(C)} 2 qquad mathrm{(D)} 3 qquad mathrm{(E)} 4$

Problem 22

A rectangular box $P$ is inscribed in a sphere of radius $r$ . The surface area of $P$ is 384, and the sum of the lengths of its 12 edges is 112. What is $r$ ?

$mathrm{(A) } 8 qquad mathrm{(B) } 10 qquad mathrm{(C) } 12 qquad mathrm{(D) } 14 qquad mathrm{(E) } 16$

Problem 23

Two distinct numbers $a$ and $b$ are chosen randomly from the set ${ 2, 2^2, 2^3, ldots, 2^{25} }$ . What is the probability that $log_{a} b$ is an integer?

$mathrm {(A) } frac{2}{25} qquad mathrm {(B) } frac{31}{300} qquad mathrm {(C) } frac{13}{100} qquad mathrm {(D) } frac{7}{50} qquad mathrm {(E) } frac{1}{2}$

Problem 24

Let $P(x) = (x - 1)(x - 2)(x - 3)$ . For how many polynomials $Q(x)$ does there exist a polynomial $R(x)$ of degree 3 such that $P(Q(x)) = P(x) cdot R(x)$ ?

$mathrm {(A) } 19 qquad mathrm {(B) } 22 qquad mathrm {(C) } 24 qquad mathrm {(D) } 27 qquad mathrm {(E) } 32$

Problem 25

Let $S$ be the set of all points with coordinates $(x,y,z)$ , where $x, y,$ and $z$ are each chosen from the set ${ 0, 1, 2}$ . How many equilateral triangles have all their vertices in $S$ ?

$mathrm {(A) } 72 qquad mathrm {(B) } 76 qquad mathrm {(C) } 80 qquad mathrm {(D) } 84 qquad mathrm {(E) } 88$

2005 AMC12 A 真题答案详细解析

$2 = frac {1}{10}x Longrightarrow x = 20,quad 2 = frac{1}{5}y Longrightarrow y = 10,quad x-y = 20 - 10=10 mathrm{(D)}$ .
$2x + 7 = 3 Longrightarrow x = -2, quad -2b - 10 = -2 Longrightarrow -2b = 8 Longrightarrow b = -4 mathrm{(B)}$
Let $w$ be the width, so the length is $2w$ . By the Pythagorean Theorem, $w^2 + 4w^2 = x^2 Longrightarrow frac{x}{sqrt{5}} = w$ . The area of the rectangle is $(w)(2w) = 2w^2 = 2left(frac{x}{sqrt{5}}right)^2 = frac{2}{5}x^2 mathrm{(B)}$ .
For $n$ windows, the store offers a discount of $100 cdot leftlfloorfrac{n}{5}rightrfloor$ (floor function). Dave receives a discount of $100 cdot leftlfloor frac{7}{5}right rfloor = 100$ and Doug receives a discount of $100 cdot leftlfloor frac{8}{5}rightrfloor = 100$ . These amount to $200$ dollars in discounts. Together, they receive a discount of $100 cdot leftlfloor frac{15}{5} rightrfloor = 300$ , so they save $300-200=100 mathrm{(A)}$ .
The sum of the first 20 numbers is $20 cdot 30$ and the sum of the other 30 numbers is $30cdot 20$ . Hence the overall average is $frac{20 cdot 30 + 30 cdot 20}{50} = 24 mathrm{(B)}$ .
Let $D_J, D_M$ be the distances traveled by Josh and Mike, respectively, and let $r,t$ be the time and rate of Mike. Using $d = rt$ , we have that $D_M = rt$ and $D_J = left(frac{4}{5}rright)left(2tright) = frac 85rt$ . Then $13 = D_M + D_J = rt + frac{8}{5}rt = frac{13}{5}rt$ $Longrightarrow rt = D_M = 5 mathrm{(B)}$ .
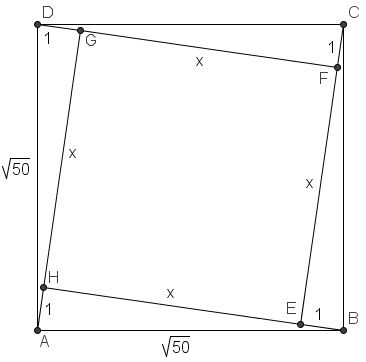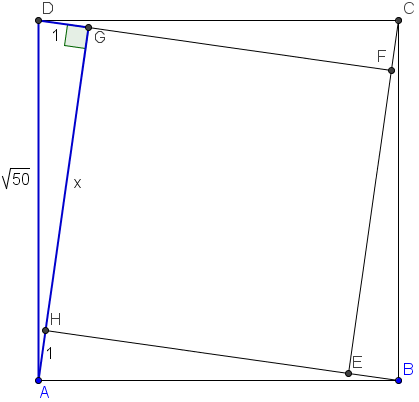Arguable the hardest part of this question is to visualize the diagram. Since each side of $EFGH$ can be extended to pass through a vertex of $ABCD$ , we realize that $EFGH$ must be tilted in such a fashion. Let a side of $EFGH$ be $x$ .Notice the right triangle (in blue) with legs $1, x+1$ and hypotenuse $sqrt{50}$ . By the Pythagorean Theorem, we have $1^2 + (x+1)^2 = (sqrt{50})^2 Longrightarrow (x+1)^2 = 49 Longrightarrow x = 6$ . Thus, $[EFGH] = x^2 = 36 mathrm{(C)}$
Clearly the two quantities are both integers, so we check the prime factorization of $2005 = 5 cdot 401$ . It is easy to see now that $(A,M,C) = (4,0,1)$ works, so the answer is $mathrm{(D)}$ .
Solution 1

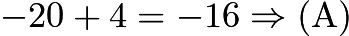A quadratic equation always has two roots, unless it has a double root. That means we can write the quadratic as a square, and the coefficients 4 and 9 suggest this. Completing the square, $0 = (2x pm 3)^2 = 4x^2 pm 12x + 9$ , so $pm 12 = a + 8 Longrightarrow a = 4, -20$ . The sum of these is $-20 + 4 = -16 Rightarrow mathrm{(A)}$ .

Solution 2

Another method would be to use the quadratic formula, since our $x^2$ coefficient is given as 4, the $x$ coefficient is $a+8$ and the constant term is $9$ . Hence, $x = frac{-(a+8) pm sqrt {(a+8)^2-4(4)(9)}}{2(4)}$ Because we want only a single solution for $x$ , the determinant must equal 0. Therefore, we can write $(a+8)^2 - 144 = 0$ which factors to $a^2 + 16a - 80 = 0$ ; using Vieta's formulas we see that the sum of the solutions for $a$ is the opposite of the coefficient of $a$ , or $-16 Rightarrow mathrm{ (A)}$ .

Solution 3

Using the discriminant, the result must equal $0$ . $D = b^2 - 4ac$ $= (a+8)^2 - 4(4)(9)$ $= a^2 + 16a + 64 - 144$ $= a^2 + 16a - 80 = 0 Rightarrow$ $(a + 20)(a - 4) = 0$ Therefore, $a = -20$ or $a = 4$ , giving a sum of $-16 Rightarrow mathrm{ (A)}$ .
There are $6n^3$ sides total on the unit cubes, and $6n^2$ are painted red. $dfrac{6n^2}{6n^3}=dfrac{1}{4} Rightarrow n=4 rightarrow mathrm {B}$
Solution 1

Let the digits be $A, B, C$ so that $B = frac {A + C}{2}$ . In order for this to be an integer, $A$ and $C$ have to have the same parity. There are $9$ possibilities for $A$ , and $5$ for $C$ . $B$ depends on the value of both $A$ and $C$ and is unique for each $(A,C)$ . Thus our answer is $9 cdot 5 cdot 1 = 45 implies E$ .

Solution 2

Thus, the three digits form an arithmetic sequence.
- If the numbers are all the same, then there are $9$ possible three-digit numbers.
- If the numbers are different, then we count the number of strictly increasing arithmetic sequences between $0$ and $10$ and multiply by 2 for the decreasing ones:
Common difference Sequences possible Number of sequences

1 $012, ldots, 789$ 8

2 $024, ldots, 579$ 6

3 $036, ldots, 369$ 4

4 $048, ldots, 159$ 2

This gives us $2(8+6+4+2) = 40$ . However, the question asks for three-digit numbers, so we have to ignore the four sequences starting with $0$ . Thus our answer is $40 + 9 - 4 = 45 Longrightarrow mathrm{(E)}$ .
For convenience’s sake, we can transform $A$ to the origin and $B$ to $(99,999)$ (this does not change the problem). The line $AB$ has the equation $y = frac{999}{99}x = frac{111}{11}x$ . The coordinates are integers if $11|x$ , so the values of $x$ are $11, 22 ldots 88$ , with a total of $8 mathrm{(D)}$ coordinates.
$(A+B) + (B+C) + (C+D) + (D+E) + (E+A) = 2(A+B+C+D+E)$ (i.e., each number is counted twice). The sum $A + B + C + D + E$ will always be $3 + 5 + 6 + 7 + 9 = 30$ , so the arithmetic sequence has a sum of $2 cdot 30 = 60$ . The middle term must be the average of the five numbers, which is $frac{60}{5} = 12 Longrightarrow mathrm{(D)}$ .

Solution 2

Let the terms in the arithmetic sequence be $a$ , $a + d$ , $a + 2d$ , $a + 3d$ , and $a + 4d$ . We seek the middle term $a + 2d$ .

These five terms are $A + B$ , $B + C$ , $C + D$ , $D + E$ , and $E + A$ , in some order. The numbers $A$ , $B$ , $C$ , $D$ , and $E$ are equal to 3, 5, 6, 7, and 9, in some order, so $[A + B + C + D + E = 3 + 5 + 6 + 7 + 9 = 30.]$ Hence, the sum of the five terms is $[(A + B) + (B + C) + (C + D) + (D + E) + (E + A) = 2A + 2B + 2C + 2D + 2E = 60.]$ But adding all five numbers, we also get $a + (a + d) + (a + 2d) + (a + 3d) + (a + 4d) = 5a + 10d$ , so $[5a + 10d = 60.]$ Dividing both sides by 5, we get $a + 2d = boxed{12}$ , which is the middle term. The answer is (D).
There are dots total. Casework:
- The dot is removed from an even face. There is a $frac{2+4+6}{21} = frac{4}{7}$ chance of this happening. Then there are 4 odd faces, giving us a probability of $frac 47 cdot frac 46 = frac{8}{21}$ .
- The dot is removed from an odd face. There is a $frac{1+3+5}{21} = frac{3}{7}$ chance of this happening. Then there are 2 odd faces, giving us a probability of $frac 37 cdot frac 26 = frac{1}{7}$ .
Thus the answer is $frac 8{21} + frac 17 = frac{11}{21} Longrightarrow mathrm{(D)}$ .
Solution 1

Notice that the bases of both triangles are diameters of the circle. Hence the ratio of the areas is just the ratio of the heights of the triangles, or $frac{CF}{CD}$ ( $F$ is the foot of the perpendicular from $C$ to $DE$ ).

Call the radius $r$ . Then $AC = frac 13(2r) = frac 23r$ , $CO = frac 13r$ . Using the Pythagorean Theorem in $triangle OCD$ , we get $frac{1}{9}r^2 + CD^2 = r^2 Longrightarrow CD = frac{2sqrt{2}}3r$ .

Now we have to find $CF$ . Notice $triangle OCD sim triangle OFC$ , so we can write the proportion:

$frac{OF}{OC} = frac{OC}{OD}$
$frac{OF}{frac{1}{3}r} = frac{frac{1}{3}r}{r}$
$OF = frac 19r$

By the Pythagorean Theorem in $triangle OFC$ , we have $left(frac{1}{9}rright)^2 + CF^2 = left(frac{1}{3}rright)^2 Longrightarrow CF = sqrt{frac{8}{81}r^2} = frac{2sqrt{2}}{9}r$ .

Our answer is $frac{CF}{CD} = frac{frac{2sqrt{2}}{9}r}{frac{2sqrt{2}}{3}r} = frac 13 Longrightarrow mathrm{(C)}$ .

Solution 2

Let the center of the circle be $O$ .

Note that $2 cdot AC = BC Rightarrow 3 cdot AC = AB$ .

$O$ is midpoint of $AB Rightarrow frac{3}{2}AC = AO Rightarrow CO = frac{1}{3}AO Rightarrow CO = frac{1}{6} AB$ .

$O$ is midpoint of $DE Rightarrow$ Area of $triangle DCE = 2 cdot$ Area of $triangle DCO = 2 cdot (frac{1}{6} cdot$ Area of $triangle ABD) = frac{1}{3} cdot$ Area of $triangle ABD Longrightarrow mathrm{(C)}$ .

Solution 3

Let $r$ be the radius of the circle. Note that $AC+BC = 2r$ so $AC = frac{2}{3}r$ .

By Power of a Point Theorem, $CD^2= AC cdot BC = 2cdot AC^2$ , and thus $CD = sqrt{2} cdot AC = frac{2sqrt{2}}{3}r$

Then the area of $triangle ABD$ is $frac{1}{2} AB cdot CD = frac{2sqrt{2}}{3}r^2$ . Similarly, the area of $triangle DCE$ is $frac{1}{2}(r-AC) cdot 2 cdot CD = frac{2sqrt{2}}{9}r^2$ , so the desired ratio is $frac{frac{2sqrt{2}}{9}r^2}{frac{2sqrt{2}}{3}r^2} = frac{1}{3} Longrightarrow mathrm{(C)}$

Solution 4

$[asy] unitsize(2.5cm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0), C=(-1/3.0), B=(1,0), A=(-1,0); pair D=dir(aCos(C.x)), e=(-D.x,-D.y); pair H=(e.x,0); draw(A--B--D--cycle); draw(D--e--C); draw(unitcircle,white); drawline(D,C); dot(O); clip(unitcircle); draw(unitcircle); label("$E$",e,SSE); label("$B$",B,NE); label("$A$",A,W); label("$D$",D,NNW); label("$C$",C,SW); label("$H$",H,SE); draw(e--H,dashed); label("O",(0,0),NE); label("1",(C--O),N); label("1",(H--O),N); label("2",(A--C),N); label("2",(H--B),N); label("3",(O--D),NE); label("3",(O--e),NE); label("$2sqrt{2}$",(D--C),W); label("$2sqrt{2}$",(H--e),E); draw(rightanglemark(e,(e.x,0),A,2)); draw(rightanglemark(D,C,B,2));[/asy]$

Let the center of the circle be $O$ . Without loss of generality, let the radius of the circle be equal to $3$ . Thus, $AO=3$ and $OB=3$ . As a consequence of $2(AC)=BC$ , $AC=2$ and $CO=1$ . Also, we know that $DO$ and $OE$ are both equal to $3$ due to the fact that they are both radii. Thus from the Pythagorean Theorem, we have DC being equal to $2005 AMC12A 真题及答案详细解析$ or $2sqrt{2}$ . Now we know that the area of $[ABD]$ is equal to $frac{(3+2+1)(2sqrt{2})}{2}$ or $6sqrt{2}$ . Know we need to find the area of $[DCE]$ . By simple inspection $[COD]$ $cong$ $[HOE]$ due to angles being equal and CPCTC. Thus $HE=2sqrt{2}$ and $OH=1$ . Know we know the area of $[CHE]=frac{(1+1)(2sqrt{2})}{2}$ or $2sqrt{2}$ . We also know that the area of $[OHE]=frac{(1)(2sqrt{2})}{2}$ or $sqrt{2}$ . Thus the area of $[COE]=2sqrt{2}-sqrt{2}$ or $sqrt{2}$ . We also can calculate the area of $[DOC]$ to be $frac{(1)(2sqrt{2})}{2}$ or $sqrt{2}$ . Thus $[DCE]$ is equal to $[COE]$ + $[DOC]$ or $sqrt{2}+sqrt{2}$ or $2sqrt{2}$ . The ratio between $[DCE]$ and $[ABD]$ is equal to $frac{2sqrt{2}}{6sqrt{2}}$ or $frac{1}{3}$ $Longrightarrow mathrm{(C)}$ .

Solution 5

We will use the shoelace formula. Our origin is the center of the circle. Denote the ordered pair for $D (x,y)$ , and notice how $E$ is a 180 degree rotation of $D$ , using the rotation matrix formula we get $E = (-x,-y)$ . WLOG say that this circle has radius $3$ . We can now find points $A$ , $B$ , and $C$ which are $(-3,0)$ , $(-1,0)$ , and $(3,0)$ respectively. By shoelace the area of $CED$ is $Y$ , and the area of $ADB$ is $3Y$ . Using division we get that the answer is $mathrm{(C)}$ .

Solution 6 (Mass Points)

$[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */ import graph; size(7cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -4.24313994860289, xmax = 6.360350402147026, ymin = -8.17642986522568, ymax = 4.1323989018072735; /* image dimensions */ pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); /* draw figures */ draw(circle((0.9223776980185863,-1.084225871478444), 3.171161249925393), linewidth(2) + wrwrwr); draw((-0.5623104956355617,1.717909856970905)--(-0.39884850438732933,-3.9670413347199647), linewidth(2) + wrwrwr); draw((-2.2487343499798245,-1.1018908670262892)--(4.0935388680341624,-1.0849377800575102), linewidth(2) + wrwrwr); draw((-0.4813673187299407,-1.0971666418223938)--(2.1729847859273126,-3.904641555130568), linewidth(2) + wrwrwr); draw((-0.5623104956355617,1.717909856970905)--(2.1561002471522333,-3.887757016355488), linewidth(2) + wrwrwr); draw((-2.2487343499798245,-1.1018908670262892)--(-0.5623104956355617,1.717909856970905), linewidth(2) + wrwrwr); draw((-0.5623104956355617,1.717909856970905)--(4.0935388680341624,-1.0849377800575102), linewidth(2) + wrwrwr); draw(circle((-2.858607769046372,-1.1524617347926092), 0.45463011998128017), linewidth(2) + wrwrwr); draw(circle((4.790088296064635,-1.144019465405069), 0.45463011998128006), linewidth(2) + wrwrwr); draw(circle((-0.9168858099122313,-1.6336710898823752), 0.45463011998127983), linewidth(2) + wrwrwr); draw(circle((1.4976032349241348,-1.3128648531558642), 0.4546301199812797), linewidth(2) + wrwrwr); draw(circle((-0.815578577261755,2.334195522261307), 0.4546301199812809), linewidth(2) + wrwrwr); draw(circle((2.6119827940793803,-4.5546962979711285), 0.45463011998128033), linewidth(2) + wrwrwr); /* dots and labels */ dot((0.9223776980185863,-1.084225871478444),dotstyle); dot((-0.5623104956355617,1.717909856970905),dotstyle); label("$D$", (-0.49477234053524466,1.8867552447217006), NE * labelscalefactor); dot((-0.39884850438732933,-3.9670413347199647),dotstyle); dot((-2.2487343499798245,-1.1018908670262892),dotstyle); label("A", (-2.183226218043193,-0.9329627307165757), NE * labelscalefactor); dot((4.0935388680341624,-1.0849377800575102),dotstyle); label("B", (4.165360361386693,-0.9160781919414961), NE * labelscalefactor); dot((-0.4813673187299407,-1.0971666418223938),linewidth(4pt) + dotstyle); label("C", (-0.41034964665984724,-0.9667318082667347), NE * labelscalefactor); dot((2.1729847859273126,-3.904641555130568),dotstyle); dot((2.1561002471522333,-3.887757016355488),dotstyle); label("E", (2.2236384022525524,-3.7189116286046926), NE * labelscalefactor); label("2", (-2.9261459241466903,-1.2031153511178476), NE * labelscalefactor,wrwrwr); label("1", (4.722550140964316,-1.186230812342768), NE * labelscalefactor,wrwrwr); label("3", (-0.9844239650125497,-1.6758824368200735), NE * labelscalefactor,wrwrwr); label("4", (1.4300650798238166,-1.355076200093563), NE * labelscalefactor,wrwrwr); label("2", (-0.8831167323620728,2.2919841753236083), NE * labelscalefactor,wrwrwr); label("2", (2.5444446389790625,-4.5969076449088275), NE * labelscalefactor,wrwrwr); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]$

We set point $A$ as a mass of 2. This means that point $B$ has a mass of $1$ since $2times{AC} = 1times{BC}$ . This implies that point $C$ has a mass of $2+1 = 3$ and the center of the circle has a mass of $3+1 = 4$ . After this, we notice that points $D$ and $E$ both must have a mass of $2$ since $2+2 = 4$ and they are both radii of the circle.

To find the ratio of the areas, we do the reciprocal of the multiplication of the mass points of DCE and the multiplication of ABD divided by each other. Which is simply $frac{3times2times2}{2times2times1}$ which is $boxed{frac{1}{3}}$ (the reciprocal of 3)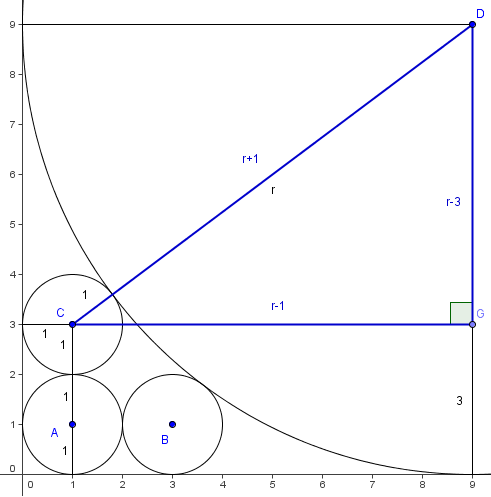
Without loss of generality, let $s = 1$ . Draw the segment between the center of the third circle and the large circle; this has length $r+1$ . We then draw the radius of the large circle that is perpendicular to the x-axis, and draw the perpendicular from this radius to the center of the third circle. This gives us a right triangle with legs $r-3,r-1$ and hypotenuse $r+1$ . The Pythagorean Theorem yields:
$(r-3)^2 + (r-1)^2 = (r+1)^2$
$r^2 - 10r + 9 = 0$
$r = 1, 9$

Quite obviously $r > s = 1$ , so $r = 9$ and $frac rs = frac 91 = 9 Longrightarrow mathrm{(D)}$ .
It is a pyramid with height $1$ and base area $frac{1}{4}$ , so using the formula for the volume of a pyramid, $frac{1}{3} cdot left(frac{1}{4}right) cdot (1) = frac {1}{12} Rightarrow boxed{(mathrm {A})}$ .
The given states that there are $168$ prime numbers less than $1000$ , which is a fact we must somehow utilize. Since there seems to be no easy way to directly calculate the number of "prime-looking" numbers, we can apply complementary counting. We can split the numbers from $1$ to $1000$ into several groups: ${1},$ ${mathrm{numbers divisible by 2 = S_2}},$ ${mathrm{numbers divisible by 3 = S_3}},$ ${mathrm{numbers divisible by 5 = S_5}}, {mathrm{primes not including 2,3,5}},$ ${mathrm{prime-looking}}$ . Hence, the number of prime-looking numbers is $1000 - 165 - 1 - |S_2 cup S_3 cup S_5|$ (note that $2,3,5$ are primes).We can calculate $S_2 cup S_3 cup S_5$ using the Principle of Inclusion-Exclusion: (the values of $|S_2| ldots$ and their intersections can be found quite easily)
$|S_2 cup S_3 cup S_5| = |S_2| + |S_3| + |S_5| - |S_2 cap S_3| - |S_3 cap S_5| - |S_2 cap S_5| + |S_2 cap S_3 cap S_5|$
$= 500 + 333 + 200 - 166 - 66 - 100 + 33 = 734$

Substituting, we find that our answer is $1000 - 165 - 1 - 734 = 100 Longrightarrow mathrm{(A)}$ .
Solution 1

We find the number of numbers with a $4$ and subtract from $2005$ . Quick counting tells us that there are $200$ numbers with a 4 in the hundreds place, $200$ numbers with a 4 in the tens place, and $201$ numbers with a 4 in the units place (counting $2004$ ). Now we apply the Principle of Inclusion-Exclusion. There are $20$ numbers with a 4 in the hundreds and in the tens, and $20$ for both the other two intersections. The intersection of all three sets is just $2$ . So we get:

$2005-(200+200+201-20-20-20+2) = 1462 Longrightarrow mathrm{(B)}$

Solution 2

Alternatively, consider that counting without the number $4$ is almost equivalent to counting in base $9$ ; only, in base $9$ , the number $9$ is not counted. Since $4$ is skipped, the symbol $5$ represents $4$ miles of travel, and we have traveled $2004_9$ miles. By basic conversion, $2004_9=9^3(2)+9^0(4)=729(2)+1(4)=1458+4=boxed{1462}$
Solution 1

For the two functions $f(x)=2x,0le xle frac{1}{2}$ and $f(x)=2-2x,frac{1}{2}le xle 1$ ,as long as $f(x)$ is between $0$ and $1$ , $x$ will be in the right domain, so we don't need to worry about the domain of $x$ .

Also, every time we change $f(x)$ , the expression for the final answer in terms of $x$ will be in a different form(although they'll all satisfy the final equation), so we get a different starting value of $x$ . Every time we have two choices for $f(x$ ) and altogether we have to choose $2005$ times. Thus, $2^{2005}Rightarrowboxed{E}$ .

Note: the values of x that satisfy $f^{[n]}(x) = frac {1}{2}$ are $frac{1}{2^{n+1}}$ , $frac{3}{2^{n+1}}$ , $frac{5}{2^{n+1}}$ , $cdots$ , $frac{2^{n+1}-1}{2^{n+1}}$ .

Solution 2

We are given that $f^{[2005]}(x) = frac {1}{2}$ . Thus, $f(f^{[2004]}(x))=frac{1}{2}$ . Let $f^{[2004]}(x)$ be equal to $y$ . Thus $f(y)=frac{1}{2}$ or $y=frac{1}{4}$ or $frac{3}{4}$ . Now we know $f^{[2004]}(x)$ is equal to $frac{1}{4}$ or $frac{3}{4}$ . Now we know that $f(f^{[2003]}(x))=frac{1}{4}$ or $frac{3}{4}$ . Now we solve for $f^{[2003]}(x)$ and let $f^{[2003]}(x)=z$ . Thus $f(z)$ is equal to $frac{1}{8}$ , $frac{7}{8}$ , $frac{5}{8}$ ,and $frac{3}{8}$ . As we see, $f^{[2005]}(x)$ has 1 solution, $f^{[2004]}(x)$ has 2 solutions, and $f^{[2003]}(x)$ has 4 solutions. Thus for each iteration we double the number of possible solutions. There are 2005 iterations and thus the number of solutions is $2^{2005}$ $Rightarrowboxed{E}$
Casework upon :
- $c = 0$ : Then $a^0 = b Longrightarrow b = 1$ . Thus we get $(2004,1,0)$ .
- $c = 1$ : Then $a^1 = b Longrightarrow a = b$ . Thus we get $(1002,1002,1)$ .
- $c ge 2$ : Then the exponent of $a$ becomes huge, and since $a ge 2$ there is no way we can satisfy the second condition. Hence we have two ordered triples $mathrm{(C)}$
Box P has dimensions $l$ , $w$ , and $h$ . Its surface area is $[2lw+2lh+2wl=384,]$ and the sum of all its edges is $[l + w + h = dfrac{4l+4w+4h}{4} = dfrac{112}{4} = 28.]$ The diameter of the sphere is the space diagonal of the prism, which is $[sqrt{l^2 + w^2 +h^2}.]$ Notice that $[(l + w + h)^2 - (2lw + 2lh + 2wh) = l^2 + w^2 + h^2 = 784 - 384 = 400,]$ so the diameter is $[sqrt{l^2 + w^2 +h^2} = sqrt{400} = 20.]$ The radius is half of the diameter, so $[r=frac{20}{2} = boxed{textbf{(B)} 10}.]$
Let $log_a b = z$ , so $a^z = b$ . Define $a = 2^x$ , $b = 2^y$ ; then $left(2^xright)^z = 2^{xz}= 2^y$ , so $x|y$ . Here we can just make a table and count the number of values of $y$ per value of $x$ . The largest possible value of $x$ is 12, and we get $sum_{x=1}^{12} lfloorfrac {25}x-1rfloor = 24 + 11 + 7 + 5 + 4 + 3 + 2 + 2 + 1 + 1 + 1 + 1 = 62$ .The total number of ways to pick two distinct numbers is $frac{25!}{(25-2)!}= 25 cdot 24 = 600$ , so we get a probability of $frac{62}{600} = boxed{textbf{(B) }frac{31}{300}}$ .
We can write the problem as

$P(Q(x))=(Q(x)-1)(Q(x)-2)(Q(x)-3)=P(x)cdot R(x)=(x-1)(x-2)(x-3)cdot R(x)$ .

Since $deg P(x) = 3$ and $deg R(x) = 3$ , $deg P(x)cdot R(x) = 6$ . Thus, $deg P(Q(x)) = 6$ , so $deg Q(x) = 2$ .

$P(Q(1))=(Q(1)-1)(Q(1)-2)(Q(1)-3)=P(1)cdot R(1)=0,$
$P(Q(2))=(Q(2)-1)(Q(2)-2)(Q(2)-3)=P(2)cdot R(2)=0,$
$P(Q(3))=(Q(3)-1)(Q(3)-2)(Q(3)-3)=P(3)cdot R(3)=0.$

Hence, we conclude $Q(1)$ , $Q(2)$ , and $Q(3)$ must each be $1$ , $2$ , or $3$ . Since a quadratic is uniquely determined by three points, there can be $3*3*3 = 27$ different quadratics $Q(x)$ after each of the values of $Q(1)$ , $Q(2)$ , and $Q(3)$ are chosen.

However, we have included $Q(x)$ which are not quadratics: lines. Namely,

$Q(1)=Q(2)=Q(3)=1 Rightarrow Q(x)=1,$
$Q(1)=Q(2)=Q(3)=2 Rightarrow Q(x)=2,$
$Q(1)=Q(2)=Q(3)=3 Rightarrow Q(x)=3,$
$Q(1)=1, Q(2)=2, Q(3)=3 Rightarrow Q(x)=x,$
$Q(1)=3, Q(2)=2, Q(3)=1 Rightarrow Q(x)=4-x.$

Clearly, we could not have included any other constant functions. For any linear function, we have $2cdot Q(2) = Q(1) + Q(3)$ because $Q(2)$ is y-value of the midpoint of $(1, Q(1))$ and $(3, Q(3))$ . So we have not included any other linear functions. Therefore, the desired answer is $27 - 5 = boxed{textbf{(B) }22}$ .
Solution 1 (non-rigorous)

For this solution, we will just find as many solutions as possible, until it becomes intuitive that there are no more size of triangles left.

First, try to make three of its vertices form an equilateral triangle. This we find is possible by taking any vertex, and connecting the three adjacent vertices into a triangle. This triangle will have a side length of $2005 AMC12A 真题及答案详细解析$ ; a quick further examination of this cube will show us that this is the only possible side length (red triangle in diagram). Each of these triangles is determined by one vertex of the cube, so in one cube we have 8 equilateral triangles. We have 8 unit cubes, and then the entire cube (green triangle), giving us 9 cubes and $9 cdot 8 = 72$ equilateral triangles.

$[asy] import three; unitsize(1cm); size(200); currentprojection=perspective(1/3,-1,1/2); draw((0,0,0)--(2,0,0)--(2,2,0)--(0,2,0)--cycle); draw((0,0,0)--(0,0,2)); draw((0,2,0)--(0,2,2)); draw((2,2,0)--(2,2,2)); draw((2,0,0)--(2,0,2)); draw((0,0,2)--(2,0,2)--(2,2,2)--(0,2,2)--cycle); draw((2,0,0)--(0,2,0)--(0,0,2)--cycle,green); draw((1,0,0)--(0,1,0)--(0,0,1)--cycle,red); label("$x=2$",(1,0,0),S); label("$z=2$",(2,2,1),E); label("$y=2$",(2,1,0),SE); [/asy]$ NOTE: Connecting the centers of the faces will actually give an octahedron, not a cube, because it only has $6$ vertices.

Now, we look for any additional equilateral triangles. Connecting the midpoints of three non-adjacent, non-parallel edges also gives us more equilateral triangles (blue triangle). Notice that picking these three edges leaves two vertices alone (labelled A and B), and that picking any two opposite vertices determine two equilateral triangles. Hence there are $frac{8 cdot 2}{2} = 8$ of these equilateral triangles, for a total of $boxed{textbf{(C) }80}$ .

$[asy] import three; unitsize(1cm); size(200); currentprojection=perspective(1/3,-1,1/2); draw((0,0,0)--(2,0,0)--(2,2,0)--(0,2,0)--cycle); draw((0,0,0)--(0,0,2)); draw((0,2,0)--(0,2,2)); draw((2,2,0)--(2,2,2)); draw((2,0,0)--(2,0,2)); draw((0,0,2)--(2,0,2)--(2,2,2)--(0,2,2)--cycle); draw((1,0,0)--(2,2,1)--(0,1,2)--cycle,blue); label("$x=2$",(1,0,0),S); label("$z=2$",(2,2,1),E); label("$y=2$",(2,1,0),SE); label("$A$",(0,2,0), NW); label("$B$",(2,0,2), NW); [/asy]$

Solution 2 (rigorous)

The three-dimensional distance formula shows that the lengths of the equilateral triangle must be $sqrt{d_x^2 + d_y^2 + d_z^2}, 0 le d_x, d_y, d_z le 2$ , which yields the possible edge lengths of

$sqrt{0^2+0^2+1^2}=sqrt{1}, sqrt{0^2+1^2+1^2}=sqrt{2}, sqrt{1^2+1^2+1^2}=sqrt{3},$ $sqrt{0^2+0^2+2^2}=sqrt{4}, sqrt{0^2+1^2+2^2}=sqrt{5}, sqrt{1^2+1^2+2^2}=sqrt{6},$ $sqrt{0^2+2^2+2^2}=sqrt{8}, sqrt{1^2+2^2+2^2}=sqrt{9}, sqrt{2^2+2^2+2^2}=sqrt{12}$ Some casework shows that $sqrt{2}, sqrt{6}, sqrt{8}$ are the only lengths that work, from which we can use the same counting argument as above.