- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2002AMC10B真题与答案解析
2002AMC10B真题
答案解析请参考文末
Problem 1
The ratio ![]() is:
is:
![]()
Problem 2
For the nonzero numbers ![]() and
and ![]() define
define![]() Find
Find ![]() .
.
![]()
Problem 3
The arithmetic mean of the nine numbers in the set ![]() is a
is a ![]() -digit number
-digit number ![]() , all of whose digits are distinct. The number
, all of whose digits are distinct. The number ![]() does not contain the digit
does not contain the digit
![]()
Problem 4
What is the value of
![]()
when ![]() ?
?
![]()
Problem 5
Circles of radius ![]() and
and ![]() are externally tangent and are circumscribed by a third circle, as shown in the figure. Find the area of the shaded region.
are externally tangent and are circumscribed by a third circle, as shown in the figure. Find the area of the shaded region.
![[asy] unitsize(5mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=4; real r1=3; real r2=2; real r3=5; pair A=(-2,0), B=(3,0), C=(0,0); pair X=(1,0), Y=(5,0); path circleA=Circle(A,r1); path circleB=Circle(B,r2); path circleC=Circle(C,r3); fill(circleC,gray); fill(circleA,white); fill(circleB,white); draw(circleA); draw(circleB); draw(circleC); draw(A--X); draw(B--Y); pair[] ps={A,B}; dot(ps); label("$3$",midpoint(A--X),N); label("$2$",midpoint(B--Y),N); [/asy]](https://latex.artofproblemsolving.com/2/c/5/2c5a7bbafa30af5c988825a58d564ad2037aaa7b.png)
Problem 6
For how many positive integers ![]() is
is ![]() a prime number?
a prime number?
![]()
Problem 7
Let ![]() be a positive integer such that
be a positive integer such that ![]() is an integer. Which of the following statements is not true?
is an integer. Which of the following statements is not true?
![]()
Problem 8
Suppose July of year ![]() has five Mondays. Which of the following must occur five times in the August of year
has five Mondays. Which of the following must occur five times in the August of year ![]() ? (Note: Both months have
? (Note: Both months have ![]() days.)
days.)
![]()
Problem 9
Using the letters ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , we can form five-letter "words". If these "words" are arranged in alphabetical order, then the "word"
, we can form five-letter "words". If these "words" are arranged in alphabetical order, then the "word" ![]() occupies position
occupies position
![]()
Problem 10
Suppose that ![]() and
and ![]() are nonzero real numbers, and that the equation
are nonzero real numbers, and that the equation ![]() has solutions
has solutions ![]() and
and ![]() . what is the pair
. what is the pair ![]() ?
?
![]()
Problem 11
The product of three consecutive positive integers is ![]() times their sum. What is the sum of their squares?
times their sum. What is the sum of their squares?
![]()
Problem 12
For which of the following values of ![]() does the equation
does the equation ![]() have no solution for
have no solution for ![]() ?
?
![]()
Problem 13
Find the value(s) of ![]() such that
such that ![]() is true for all values of
is true for all values of ![]() .
.
![]()
Problem 14
The number ![]() is the square of a positive integer
is the square of a positive integer ![]() . In decimal representation, the sum of the digits of
. In decimal representation, the sum of the digits of ![]() is
is
![]()
Problem 15
The positive integers ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are all prime numbers. The sum of these four primes is
are all prime numbers. The sum of these four primes is
![]()
Problem 16
For how many integers ![]() is
is ![]() the square of an integer?
the square of an integer?
![]()
Problem 17
A regular octagon ![]() has sides of length two. Find the area of
has sides of length two. Find the area of ![]() .
.
![]()
Problem 18
Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?
![]()
Problem 19
Suppose that ![]() is an arithmetic sequence with
is an arithmetic sequence with![]() What is the value of
What is the value of ![]()
![]()
Problem 20
Let ![]() and
and ![]() be real numbers such that
be real numbers such that ![]() and
and ![]() Then
Then ![]() is
is
![]()
Problem 21
Andy's lawn has twice as much area as Beth's lawn and three times as much as Carlos' lawn. Carlos' lawn mower cuts half as fast as Beth's mower and one third as fast as Andy's mower. If they all start to mow their lawns at the same time, who will finish first?
![]()
Problem 22
Let ![]() be a right-angled triangle with
be a right-angled triangle with ![]() . Let
. Let ![]() and
and ![]() be the midpoints of the legs
be the midpoints of the legs ![]() and
and ![]() , respectively. Given
, respectively. Given ![]() and
and ![]() , find
, find ![]() .
.
![]()
Problem 23
Let ![]() be a sequence of integers such that
be a sequence of integers such that ![]() and
and ![]() for all positive integers
for all positive integers ![]() and
and ![]() Then
Then ![]() is
is
![]()
Problem 24
Riders on a Ferris wheel travel in a circle in a vertical plane. A particular wheel has radius ![]() feet and revolves at the constant rate of one revolution per minute. How many seconds does it take a rider to travel from the bottom of the wheel to a point
feet and revolves at the constant rate of one revolution per minute. How many seconds does it take a rider to travel from the bottom of the wheel to a point ![]() vertical feet above the bottom?
vertical feet above the bottom?
![]()
Problem 25
When ![]() is appended to a list of integers, the mean is increased by
is appended to a list of integers, the mean is increased by ![]() . When
. When ![]() is appended to the enlarged list, the mean of the enlarged list is decreased by
is appended to the enlarged list, the mean of the enlarged list is decreased by ![]() . How many integers were in the original list?
. How many integers were in the original list?
![]()
2002AMC10B详细解析
 or
or 

- We wish to find
 , or
, or  . This does not have the digit 0, so the answer is
. This does not have the digit 0, so the answer is  Notice that the final number is guaranteed to have the digits
Notice that the final number is guaranteed to have the digits  and that each of these digits can be paired with an even number adding up to 9.
and that each of these digits can be paired with an even number adding up to 9.  can be taken out, with the other digits fulfilling divisibility by 9.
can be taken out, with the other digits fulfilling divisibility by 9. ![$(3x-2)[(4x+1)-4x] + 1 = 3x-2 + 1 = 3x-1 = 3(4) - 1 = boxed{mathrm{(D)} 11}$](https://latex.artofproblemsolving.com/a/a/0/aa01f3de68b8e5cb8901b61622119f3327d4c7e0.png) .
.- A line going through the centers of the two smaller circles also go through the diameter. The length of this line within the circle is
 Because this is the length of the larger circle's diameter, the length of its radius is
Because this is the length of the larger circle's diameter, the length of its radius is  The area of the large circle is
The area of the large circle is  , and the area of the two smaller circles is
, and the area of the two smaller circles is  To find the area of the shaded region, subtract the area of the two smaller circles from the area of the large circle.
To find the area of the shaded region, subtract the area of the two smaller circles from the area of the large circle. 
- Factoring, we get
 . Either
. Either  or
or  is odd, and the other is even. Their product must yield an even number. The only prime that is even is
is odd, and the other is even. Their product must yield an even number. The only prime that is even is  , which is when
, which is when  is
is  . The answer is
. The answer is  .Considering parity, we see that
.Considering parity, we see that  is always even. The only even prime is
is always even. The only even prime is  , and so
, and so  whence
whence  .
. - Since
 ,
,![[0 < lim_{n rightarrow infty} left(frac{41}{42} + frac{1}{n}right) < frac {41}{42} + frac 1n < frac{41}{42} + frac 11 < 2]](https://latex.artofproblemsolving.com/0/a/1/0a117286e3f8f0f84a7cbc59b1204f101146fc51.png) From which it follows that
From which it follows that  and
and  . The only answer choice that is not true is
. The only answer choice that is not true is  .
. - If there are five Mondays, there are only three possibilities for their dates:
 ,
,  , and
, and  .In the first case August starts on a Thursday, and there are five Thursdays, Fridays, and Saturdays in August.In the second case August starts on a Wednesday, and there are five Wednesdays, Thursdays, and Fridays in August.In the third case August starts on a Tuesday, and there are five Tuesdays, Wednesdays, and Thursdays in August.The only day of the week that is guaranteed to appear five times is therefore
.In the first case August starts on a Thursday, and there are five Thursdays, Fridays, and Saturdays in August.In the second case August starts on a Wednesday, and there are five Wednesdays, Thursdays, and Fridays in August.In the third case August starts on a Tuesday, and there are five Tuesdays, Wednesdays, and Thursdays in August.The only day of the week that is guaranteed to appear five times is therefore  .
. - There are
 "words" beginning with each of the first four letters alphabetically. From there, there are
"words" beginning with each of the first four letters alphabetically. From there, there are  with
with  as the first letter and each of the first three letters alphabetically. After that, the next "word" is
as the first letter and each of the first three letters alphabetically. After that, the next "word" is  , hence our answer is
, hence our answer is  .Let
.Let  . Then counting backwards,
. Then counting backwards,  , so the answer is
, so the answer is 
- Since
 , it follows by comparing coefficients that
, it follows by comparing coefficients that  and that
and that  . Since
. Since  is nonzero,
is nonzero,  , and
, and  . Thus
. Thus  .Another method is to use Vieta's formulas. The sum of the solutions to this polynomial is equal to the opposite of the
.Another method is to use Vieta's formulas. The sum of the solutions to this polynomial is equal to the opposite of the  coefficient, since the leading coefficient is 1; in other words,
coefficient, since the leading coefficient is 1; in other words,  and the product of the solutions is equal to the constant term (i.e,
and the product of the solutions is equal to the constant term (i.e,  ). Since
). Since  is nonzero, it follows that
is nonzero, it follows that  and therefore (from the first equation),
and therefore (from the first equation),  . Hence,
. Hence,  Note that for roots
Note that for roots  and
and  ,
,  . This implies that
. This implies that  is
is  , and there is only one answer choice with
, and there is only one answer choice with  in the position for
in the position for  , hence,
, hence, 
- Let the three consecutive positive integers be
 ,
,  , and
, and  . So,
. So,  .
.  , so
, so  . Hence, the sum of the squares is
. Hence, the sum of the squares is  .
. - The domain over which we solve the equation is
 .We can now cross-multiply to get rid of the fractions, we get
.We can now cross-multiply to get rid of the fractions, we get  .Simplifying that, we get
.Simplifying that, we get  . Clearly for
. Clearly for  we get the equation
we get the equation  which is never true. The answer is
which is never true. The answer is  For other
For other  , one can solve for
, one can solve for  :
:  , hence
, hence  . We can easily verify that for none of the other four possible values of
. We can easily verify that for none of the other four possible values of  is this equal to
is this equal to  or
or  , hence there is a solution for
, hence there is a solution for  in each of the other cases.
in each of the other cases. - We have
 .As
.As  must be true for all
must be true for all  , we must have
, we must have  , hence
, hence  .Since we want only the
.Since we want only the  -variable to be present, we move the terms only with the
-variable to be present, we move the terms only with the  -variable to one side, thus constructing
-variable to one side, thus constructing  to
to  . For there to be infinite solutions for
. For there to be infinite solutions for  and there is no
and there is no  , we simply find a value of
, we simply find a value of  such that the equation is symmetrical. Therefore,
such that the equation is symmetrical. Therefore,
 There is only one solution, namely
There is only one solution, namely  or
or 
- Taking the root, we get
 .Now, we have
.Now, we have  .Combining the
.Combining the  's and
's and  's gives us
's gives us  .This is the number
.This is the number  with a string of sixty-four
with a string of sixty-four  's at the end. Thus, the sum of the digits of
's at the end. Thus, the sum of the digits of  is
is 
- Since
 and
and  must have the same parity, and since there is only one even prime number, it follows that
must have the same parity, and since there is only one even prime number, it follows that  and
and  are both odd. Thus one of
are both odd. Thus one of  is odd and the other even. Since
is odd and the other even. Since  , it follows that
, it follows that  (as a prime greater than
(as a prime greater than  ) is odd. Thus
) is odd. Thus  , and
, and  are consecutive odd primes. At least one of
are consecutive odd primes. At least one of  is divisible by
is divisible by  , from which it follows that
, from which it follows that  and
and  . The sum of these numbers is thus
. The sum of these numbers is thus  , a prime, so the answer is
, a prime, so the answer is  .In order for both
.In order for both  and
and  to be prime, one of
to be prime, one of  must be 2, or else both
must be 2, or else both  ,
,  would be even numbers.If
would be even numbers.If  , then
, then  and
and  , which is not possible. Thus
, which is not possible. Thus  .Since
.Since  is prime and
is prime and  , we can infer that
, we can infer that  and thus
and thus  can be expressed as
can be expressed as  for some natural number
for some natural number  .However in either case, one of
.However in either case, one of  and
and  can be expressed as
can be expressed as  which is a multiple of 3. Therefore the only possibility that works is when
which is a multiple of 3. Therefore the only possibility that works is when  and
and![[A + B + (A - B) + (A + B) = 5 + 2 + 3 + 7 = 17]](https://latex.artofproblemsolving.com/0/0/9/009d79e62fcb86d45c7d973d181b0c3b8d45bb69.png) Which is a prime number.
Which is a prime number. 
- Let
 , with
, with  (note that the solutions
(note that the solutions  do not give any additional solutions for
do not give any additional solutions for  ). Then rewriting,
). Then rewriting,  . Since
. Since  , it follows that
, it follows that  divides
divides  . Listing the factors of
. Listing the factors of  , we find that
, we find that  are the only
are the only  solutions (respectively yielding
solutions (respectively yielding  ).For
).For  and
and  the fraction is negative, for
the fraction is negative, for  it is not defined, and for
it is not defined, and for  it is between 0 and 1.Thus we only need to examine
it is between 0 and 1.Thus we only need to examine  and
and  .For
.For  and
and  we obviously get the squares
we obviously get the squares  and
and  respectively.For prime
respectively.For prime  the fraction will not be an integer, as the denominator will not contain the prime in the numerator.This leaves
the fraction will not be an integer, as the denominator will not contain the prime in the numerator.This leaves  , and a quick substitution shows that out of these only
, and a quick substitution shows that out of these only  and
and  yield a square. Therefore, there are only
yield a square. Therefore, there are only  solutions (respectively yielding
solutions (respectively yielding  ).If
).If  , then
, then  and
and  , otherwise
, otherwise  will be negative. Thus
will be negative. Thus  and
and![[0 = frac{0}{20-(0)} le frac{n}{20-n} le frac{19}{20-(19)} = 19]](https://latex.artofproblemsolving.com/9/f/e/9feb430d115aea0e9e86b02cdd2ae225b49642b5.png) Checking all
Checking all  for which
for which  , we have
, we have  ,
,  ,
,  ,
,  as the possibilities.
as the possibilities. 
- The area of the triangle
 can be computed as
can be computed as  . We will now find
. We will now find  and
and  .Clearly,
.Clearly,  is a right isosceles triangle with hypotenuse of length
is a right isosceles triangle with hypotenuse of length  , hence
, hence  . The same holds for triangle
. The same holds for triangle  and its leg
and its leg  . The length of
. The length of  is equal to
is equal to  . Hence
. Hence  , and
, and  .Then the area of
.Then the area of  equals
equals  .
. - For any given pair of circles, they can intersect at most
 times. Since there are
times. Since there are  pairs of circles, the maximum number of possible intersections is
pairs of circles, the maximum number of possible intersections is  . We can construct such a situation as below, so the answer is
. We can construct such a situation as below, so the answer is  .
.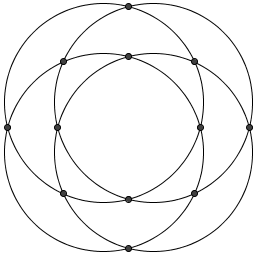 Because a pair or circles can intersect at most
Because a pair or circles can intersect at most  times, the first circle can intersect the second at
times, the first circle can intersect the second at  points, the third can intersect the first two at
points, the third can intersect the first two at  points, and the fourth can intersect the first three at
points, and the fourth can intersect the first three at  points. This means that our answer is
points. This means that our answer is  Pick a circle any circle-
Pick a circle any circle-  ways. Then, pick any other circle-
ways. Then, pick any other circle-  ways. For each of these circles, there will be
ways. For each of these circles, there will be  intersections for a total of
intersections for a total of  =
=  intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of
intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of  , which corresponds to
, which corresponds to  .
. - We should realize that the two equations are 100 terms apart, so by subtracting the two equations in a form like...
 ...we get the value of the common difference of every hundred terms hundred times. So we have to divide the answer by hundred to get ...
...we get the value of the common difference of every hundred terms hundred times. So we have to divide the answer by hundred to get ... ...the common difference of every hundred terms. Then we have to simply divide the answer by hundred again to find the common difference between one term, therefore...
...the common difference of every hundred terms. Then we have to simply divide the answer by hundred again to find the common difference between one term, therefore...

Adding the two given equations together gives
 .
.Now, let the common difference be
 . Notice that
. Notice that  , so we merely need to find
, so we merely need to find  to get the answer. The formula for an arithmetic sum is
to get the answer. The formula for an arithmetic sum is ,
,where
 is the first term,
is the first term,  is the number of terms, and
is the number of terms, and  is the common difference. Now we use this formula to find a closed form for the first given equation and the sum of the given equations. For the first equation, we have
is the common difference. Now we use this formula to find a closed form for the first given equation and the sum of the given equations. For the first equation, we have  . Therefore, we have
. Therefore, we have ,
,or
 . *(1)
. *(1)For the sum of the equations (shown at the beginning of the solution) we have
 , so
, so
or
 *(2)
*(2)Now we have a system of equations in terms of
 and
and  . Subtracting (1) from (2) eliminates
. Subtracting (1) from (2) eliminates  , yielding
, yielding  , and
, and  .
.Subtracting the 2 given equations yields

Now express each
 in terms of first term
in terms of first term  and common difference
and common difference  between consecutive terms
between consecutive terms
Simplifying and canceling
 and
and  terms gives
terms gives



- Rearranging, we get
 and
and  Squaring both,
Squaring both,  and
and  are obtained.Adding the two equations and dividing by
are obtained.Adding the two equations and dividing by  gives
gives  , so
, so  .The easiest way is to assume a value for
.The easiest way is to assume a value for  and then solving the system of equations. For
and then solving the system of equations. For  , we get the equations
, we get the equations and
and
Multiplying the second equation by
 , we have
, we have
Adding up the two equations yields
 , so
, so 
We obtain
 after plugging in the value for
after plugging in the value for  .
.Therefore,
 which corresponds to
which corresponds to  .
. - We say Andy's lawn has an area of
 . Beth's lawn thus has an area of
. Beth's lawn thus has an area of  , and Carlos's lawn has an area of
, and Carlos's lawn has an area of  .We say Andy's lawn mower cuts at a speed of
.We say Andy's lawn mower cuts at a speed of  . Carlos's cuts at a speed of
. Carlos's cuts at a speed of  , and Beth's cuts at a speed
, and Beth's cuts at a speed  .Each person's lawn is cut at a speed of
.Each person's lawn is cut at a speed of  , so Andy's is cut in
, so Andy's is cut in  time, as is Carlos's. Beth's is cut in
time, as is Carlos's. Beth's is cut in  , so the first one to finish is
, so the first one to finish is  .
. 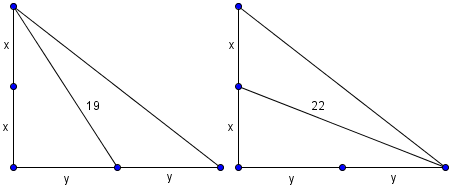 Let
Let  ,
,  . By the Pythagorean Theorem on
. By the Pythagorean Theorem on  respectively,
respectively, Summing these gives
Summing these gives  .By the Pythagorean Theorem again, we have
.By the Pythagorean Theorem again, we have![[(2x)^2 + (2y)^2 = XY^2 Longrightarrow XY = sqrt{4(x^2 + y^2)} = sqrt{4(169)} = sqrt{676} = boxed{mathrm{(B)} 26}]](https://latex.artofproblemsolving.com/f/1/6/f16445ea2f3d51273e055db6c290c3f43c9d12d2.png) Alternatively, we could note that since we found
Alternatively, we could note that since we found  , segment
, segment  . Right triangles
. Right triangles  and
and  are similar by Leg-Leg with a ratio of
are similar by Leg-Leg with a ratio of  , so
, so 
- When
 ,
,  . Hence,
. Hence,![[a_{2}=1+a_1+2]](https://latex.artofproblemsolving.com/8/9/6/89690c735df48656e99be995bfc1b51ae9309078.png)
![[a_{3}=1+a_2+3]](https://latex.artofproblemsolving.com/6/2/5/62550c6c9a0eaad755a6e3c025445f1f6d4cf158.png)
![[a_{4}=1+a_3+4]](https://latex.artofproblemsolving.com/e/3/3/e33fbf139288a9b2002a876b9b63c0b60966385f.png)
![[dots]](https://latex.artofproblemsolving.com/1/6/7/16762e47f22f53e2431935f211fa82570b46b6cb.png)
![[a_{12}=1+a_{11}+11]](https://latex.artofproblemsolving.com/1/a/0/1a0b1067f595a8c0e8a661368a8ca69a9a568797.png) Adding these equations up, we have that
Adding these equations up, we have that  ~AopsUser101Substituting
~AopsUser101Substituting  into
into  :
:  . Since
. Since  ,
,  . Therefore,
. Therefore,  , and so on until
, and so on until  . Adding the Left Hand Sides of all of these equations gives
. Adding the Left Hand Sides of all of these equations gives  ; adding the Right Hand Sides of these equations gives
; adding the Right Hand Sides of these equations gives  . These two expressions must be equal; hence
. These two expressions must be equal; hence  and
and  . Substituting
. Substituting  :
:  . Thus we have a general formula for
. Thus we have a general formula for  and substituting
and substituting  :
:  .We can literally just plug stuff in. No prerequisite is actually said in the sequence. Since
.We can literally just plug stuff in. No prerequisite is actually said in the sequence. Since  , we know
, we know  . After this, we can use
. After this, we can use  to find
to find  .
.  . Now, we can use
. Now, we can use  and
and  to find
to find  , or
, or  . Lastly, we can use
. Lastly, we can use  to find
to find  .
. 
- We can let this circle represent the ferris wheel with center
 and
and  represent the desired point
represent the desired point  feet above the bottom. Draw a diagram like the one above. We find out
feet above the bottom. Draw a diagram like the one above. We find out  is a
is a  triangle. That means
triangle. That means  and the ferris wheel has made
and the ferris wheel has made  of a revolution. Therefore, the time it takes to travel that much of a distance is
of a revolution. Therefore, the time it takes to travel that much of a distance is  of a minute, or
of a minute, or  seconds. The answer is
seconds. The answer is  . Alternatively, we could also say that
. Alternatively, we could also say that  is congruent to
is congruent to  by SAS, so
by SAS, so  is 20, and
is 20, and  is equilateral, and
is equilateral, and 
- Let
 be the sum of the integers and
be the sum of the integers and  be the number of elements in the list. Then we get the equations
be the number of elements in the list. Then we get the equations  and
and  . With a lot of algebra, the solution is found to be
. With a lot of algebra, the solution is found to be  .
.
We let ![]() be the original number of elements in the set and we let
be the original number of elements in the set and we let ![]() be the original average of the terms of the original list. Then we have
be the original average of the terms of the original list. Then we have ![]() is the sum of all the elements of the list. So we have two equations:
is the sum of all the elements of the list. So we have two equations:![]() and
and![]() Simplifying both equations and we get,
Simplifying both equations and we get,![]()
![]() Solving for
Solving for ![]() and
and ![]() , we get
, we get ![]() and
and ![]() .
.
Warning: This solution will rarely ever work in any other case. However, seeing that you can so easily plug and chug in probem 25 it is funny to see this.
Plug and chug random numbers with the answer choices, starting with the choice of ![]() numbers. You see that if you have 4 5s and you add 15 to the set, the resulting mean will be 7; we can verify this with math
numbers. You see that if you have 4 5s and you add 15 to the set, the resulting mean will be 7; we can verify this with math![]() adding in 1 to the set you result in the mean to be 6.
adding in 1 to the set you result in the mean to be 6.![]() Thus we conclude that 4 is the correct choice or
Thus we conclude that 4 is the correct choice or ![]()
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









