Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2003AMC10A真题与答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月5日上午11:48

2003AMC10A真题

答案解析请参考文末

Problem 1

What is the difference between the sum of the first $2003$ even counting numbers and the sum of the first $2003$ odd counting numbers?

$mathrm{(A) } 0qquad mathrm{(B) } 1qquad mathrm{(C) } 2qquad mathrm{(D) } 2003qquad mathrm{(E) } 4006$

Problem 2

Members of the Rockham Soccer League buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the League?

$mathrm{(A) } 77qquad mathrm{(B) } 91qquad mathrm{(C) } 143qquad mathrm{(D) } 182qquad mathrm{(E) } 286$

Problem 3

A solid box is $15$ cm by $10$ cm by $8$ cm. A new solid is formed by removing a cube $3$ cm on a side from each corner of this box. What percent of the original volume is removed?

$mathrm{(A) } 4.5qquad mathrm{(B) } 9qquad mathrm{(C) } 12qquad mathrm{(D) } 18qquad mathrm{(E) } 24$

Problem 4

It takes Mary $30$ minutes to walk uphill $1$ km from her home to school, but it takes her only $10$ minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?

$mathrm{(A) } 3qquad mathrm{(B) } 3.125qquad mathrm{(C) } 3.5qquad mathrm{(D) } 4qquad mathrm{(E) } 4.5$

Problem 5

Let $d$ and $e$ denote the solutions of $2x^{2}+3x-5=0$ . What is the value of $(d-1)(e-1)$ ?

$mathrm{(A) } -frac{5}{2}qquad mathrm{(B) } 0qquad mathrm{(C) } 3qquad mathrm{(D) } 5qquad mathrm{(E) } 6$

Problem 6

Define $x heartsuit y$ to be $|x-y|$ for all real numbers $x$ and $y$ . Which of the following statements is not true?

$mathrm{(A) } x heartsuit y = y heartsuit x$ for all $x$ and $y$

$mathrm{(B) } 2(x heartsuit y) = (2x) heartsuit (2y)$ for all $x$ and $y$

$mathrm{(C) } x heartsuit 0 = x$ for all $x$

$mathrm{(D) } x heartsuit x = 0$ for all $x$

$mathrm{(E) } x heartsuit y > 0$ if $x neq y$

Problem 7

How many non-congruent triangles with perimeter $7$ have integer side lengths?

$mathrm{(A) } 1qquad mathrm{(B) } 2qquad mathrm{(C) } 3qquad mathrm{(D) } 4qquad mathrm{(E) } 5$

Problem 8

What is the probability that a randomly drawn positive factor of $60$ is less than $7$ ?

$mathrm{(A) } frac{1}{10}qquad mathrm{(B) } frac{1}{6}qquad mathrm{(C) } frac{1}{4}qquad mathrm{(D) } frac{1}{3}qquad mathrm{(E) } frac{1}{2}$

Problem 9

Simplify

$sqrt[3]{xsqrt[3]{xsqrt[3]{xsqrt{x}}}}$ .

$mathrm{(A) } sqrt{x}qquad mathrm{(B) } sqrt[3]{x^{2}}qquad mathrm{(C) } sqrt[27]{x^{2}}qquad mathrm{(D) } sqrt[54]{x}qquad mathrm{(E) } sqrt[81]{x^{80}}$

Problem 10

The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?

$[asy] unitsize(10mm); defaultpen(fontsize(10pt)); pen finedashed=linetype("4 4"); filldraw((1,1)--(2,1)--(2,2)--(4,2)--(4,3)--(1,3)--cycle,grey,black+linewidth(.8pt)); draw((0,1)--(0,3)--(1,3)--(1,4)--(4,4)--(4,3)-- (5,3)--(5,2)--(4,2)--(4,1)--(2,1)--(2,0)--(1,0)--(1,1)--cycle,finedashed); draw((0,2)--(2,2)--(2,4),finedashed); draw((3,1)--(3,4),finedashed); label("$1$",(1.5,0.5)); draw(circle((1.5,0.5),.17)); label("$2$",(2.5,1.5)); draw(circle((2.5,1.5),.17)); label("$3$",(3.5,1.5)); draw(circle((3.5,1.5),.17)); label("$4$",(4.5,2.5)); draw(circle((4.5,2.5),.17)); label("$5$",(3.5,3.5)); draw(circle((3.5,3.5),.17)); label("$6$",(2.5,3.5)); draw(circle((2.5,3.5),.17)); label("$7$",(1.5,3.5)); draw(circle((1.5,3.5),.17)); label("$8$",(0.5,2.5)); draw(circle((0.5,2.5),.17)); label("$9$",(0.5,1.5)); draw(circle((0.5,1.5),.17));[/asy]$

$mathrm{(A) } 2qquad mathrm{(B) } 3qquad mathrm{(C) } 4qquad mathrm{(D) } 5qquad mathrm{(E) } 6$

Problem 11

The sum of the two 5-digit numbers $AMC10$ and $AMC12$ is $123422$ . What is $A+M+C$ ?

$mathrm{(A) } 10qquad mathrm{(B) } 11qquad mathrm{(C) } 12qquad mathrm{(D) } 13qquad mathrm{(E) } 14$

Problem 12

A point $(x,y)$ is randomly picked from inside the rectangle with vertices $(0,0)$ , $(4,0)$ , $(4,1)$ , and $(0,1)$ . What is the probability that $x<y$ ?

$mathrm{(A) } frac{1}{8}qquad mathrm{(B) } frac{1}{4}qquad mathrm{(C) } frac{3}{8}qquad mathrm{(D) } frac{1}{2}qquad mathrm{(E) } frac{3}{4}$

Problem 13

The sum of three numbers is $20$ . The first is four times the sum of the other two. The second is seven times the third. What is the product of all three?

$mathrm{(A) } 28qquad mathrm{(B) } 40qquad mathrm{(C) } 100qquad mathrm{(D) } 400qquad mathrm{(E) } 800$

Problem 14

Let $n$ be the largest integer that is the product of exactly 3 distinct prime numbers $d$ , $e$ , and $10d+e$ , where $d$ and $e$ are single digits. What is the sum of the digits of $n$ ?

$mathrm{(A) } 12qquad mathrm{(B) } 15qquad mathrm{(C) } 18qquad mathrm{(D) } 21qquad mathrm{(E) } 24$

Problem 15

What is the probability that an integer in the set ${1,2,3,...,100}$ is divisible by $2$ and not divisible by $3$ ?

$mathrm{(A) } frac{1}{6}qquad mathrm{(B) } frac{33}{100}qquad mathrm{(C) } frac{17}{50}qquad mathrm{(D) } frac{1}{2}qquad mathrm{(E) } frac{18}{25}$

Problem 16

What is the units digit of $13^{2003}$ ?

$mathrm{(A) } 1qquad mathrm{(B) } 3qquad mathrm{(C) } 7qquad mathrm{(D) } 8qquad mathrm{(E) } 9$

Problem 17

The number of inches in the perimeter of an equilateral triangle equals the number of square inches in the area of its circumscribed circle. What is the radius, in inches, of the circle?

$mathrm{(A) } frac{3sqrt{2}}{pi}qquad mathrm{(B) } frac{3sqrt{3}}{pi}qquad mathrm{(C) } sqrt{3}qquad mathrm{(D) } frac{6}{pi}qquad mathrm{(E) } sqrt{3}pi$

Problem 18

What is the sum of the reciprocals of the roots of the equation

$frac{2003}{2004}x+1+frac{1}{x}=0$ ?

$mathrm{(A) } -frac{2004}{2003}qquad mathrm{(B) } -1qquad mathrm{(C) } frac{2003}{2004}qquad mathrm{(D) } 1qquad mathrm{(E) } frac{2004}{2003}$

Problem 19

A semicircle of diameter $1$ sits at the top of a semicircle of diameter $2$ , as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.

$mathrm{(A) } frac{1}{6}pi-frac{sqrt{3}}{4}qquad mathrm{(B) } frac{sqrt{3}}{4}-frac{1}{12}piqquad mathrm{(C) } frac{sqrt{3}}{4}-frac{1}{24}piqquad mathrm{(D) } frac{sqrt{3}}{4}+frac{1}{24}piqquad mathrm{(E) } frac{sqrt{3}}{4}+frac{1}{12}pi$

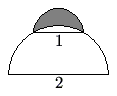
Problem 20

A base-10 three digit number $n$ is selected at random. Which of the following is closest to the probability that the base-9 representation and the base-11 representation of $n$ are both three-digit numerals?

$mathrm{(A) } 0.3qquad mathrm{(B) } 0.4qquad mathrm{(C) } 0.5qquad mathrm{(D) } 0.6qquad mathrm{(E) } 0.7$

Problem 21

Pat is to select six cookies from a tray containing only chocolate chip, oatmeal, and peanut butter cookies. There are at least six of each of these three kinds of cookies on the tray. How many different assortments of six cookies can be selected?

$mathrm{(A) } 22qquad mathrm{(B) } 25qquad mathrm{(C) } 27qquad mathrm{(D) } 28qquad mathrm{(E) } 729$

Problem 22

In rectangle $ABCD$ , we have $AB=8$ , $BC=9$ , $H$ is on $BC$ with $BH=6$ , $E$ is on $AD$ with $DE=4$ , line $EC$ intersects line $AH$ at $G$ , and $F$ is on line $AD$ with $GF perp AF$ . Find the length of $GF$ .

$[asy] unitsize(3mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair D=(0,0), Ep=(4,0), A=(9,0), B=(9,8), H=(3,8), C=(0,8), G=(-6,20), F=(-6,0); draw(D--A--B--C--D--F--G--Ep); draw(A--G); label("$F$",F,W); label("$G$",G,W); label("$C$",C,WSW); label("$H$",H,NNE); label("$6$",(6,8),N); label("$B$",B,NE); label("$A$",A,SW); label("$E$",Ep,S); label("$4$",(2,0),S); label("$D$",D,S);[/asy]$

$mathrm{(A) } 16qquad mathrm{(B) } 20qquad mathrm{(C) } 24qquad mathrm{(D) } 28qquad mathrm{(E) } 30$

Problem 23

A large equilateral triangle is constructed by using toothpicks to create rows of small equilateral triangles. For example, in the figure we have $3$ rows of small congruent equilateral triangles, with $5$ small triangles in the base row. How many toothpicks would be needed to construct a large equilateral triangle if the base row of the triangle consists of $2003$ small equilateral triangles?

$[asy] unitsize(15mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); pair Ap=(0,0), Bp=(1,0), Cp=(2,0), Dp=(3,0), Gp=dir(60); pair Fp=shift(Gp)*Bp, Ep=shift(Gp)*Cp; pair Hp=shift(Gp)*Gp, Ip=shift(Gp)*Fp; pair Jp=shift(Gp)*Hp; pair[] points={Ap,Bp,Cp,Dp,Ep,Fp,Gp,Hp,Ip,Jp}; draw(Ap--Dp--Jp--cycle); draw(Gp--Bp--Ip--Hp--Cp--Ep--cycle); for(pair p : points) { fill(circle(p, 0.07),white); } pair[] Cn=new pair[5]; Cn[0]=centroid(Ap,Bp,Gp); Cn[1]=centroid(Gp,Bp,Fp); Cn[2]=centroid(Bp,Fp,Cp); Cn[3]=centroid(Cp,Fp,Ep); Cn[4]=centroid(Cp,Ep,Dp); label("$1$",Cn[0]); label("$2$",Cn[1]); label("$3$",Cn[2]); label("$4$",Cn[3]); label("$5$",Cn[4]); for (pair p : Cn) { draw(circle(p,0.1)); }[/asy]$ $mathrm{(A) } 1,004,004 qquad mathrm{(B) } 1,005,006 qquad mathrm{(C) } 1,507,509 qquad mathrm{(D) } 3,015,018 qquad mathrm{(E) } 6,021,018$

Problem 24

Sally has five red cards numbered $1$ through $5$ and four blue cards numbered $3$ through $6$ . She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?

$mathrm{(A) } 8qquad mathrm{(B) } 9qquad mathrm{(C) } 10qquad mathrm{(D) } 11qquad mathrm{(E) } 12$

Problem 25

Let $n$ be a $5$ -digit number, and let $q$ and $r$ be the quotient and the remainder, respectively, when $n$ is divided by $100$ . For how many values of $n$ is $q+r$ divisible by $11$ ?

$mathrm{(A) } 8180qquad mathrm{(B) } 8181qquad mathrm{(C) } 8182qquad mathrm{(D) } 9000qquad mathrm{(E) } 9090$

2003AMC10A详细解析

The first $2003$ even counting numbers are $2,4,6,...,4006$ .The first $2003$ odd counting numbers are $1,3,5,...,4005$ .Thus, the problem is asking for the value of $(2+4+6+...+4006)-(1+3+5+...+4005)$ . $(2+4+6+...+4006)-(1+3+5+...+4005) = (2-1)+(4-3)+(6-5)+...+(4006-4005)$ $= 1+1+1+...+1 = boxed{mathrm{(D)} 2003}$ Using the sum of an arithmetic progression formula, we can write this as $frac{2003}{2}(2 + 4006) - frac{2003}{2}(1 + 4005) = frac{2003}{2} cdot 2 = boxed{mathrm{(D)} 2003}$ .
The formula for the sum of the first $n$ even numbers, is $S_E=n^{2}+n$ , (E standing for even).

Sum of first $n$ odd numbers, is $S_O=n^{2}$ , (O standing for odd).

Knowing this, plug $2003$ for $n$ ,

$S_E-S_O= (2003^{2}+2003)-(2003^{2})=2003 Rightarrow$ $boxed{mathrm{(D)} 2003}$ .
Since T-shirts cost $5$ dollars more than a pair of socks, T-shirts cost $5+4=9$ dollars.Since each member needs $2$ pairs of socks and $2$ T-shirts, the total cost for $1$ member is $2(4+9)=26$ dollars.Since $2366$ dollars was the cost for the club, and $26$ was the cost per member, the number of members in the League is $2366div 26=boxed{mathrm{(B)} 91}$ .
The volume of the original box is $15cdot10cdot8=1200$ The volume of each cube that is removed is $3cdot3cdot3=27$ Since there are $8$ corners on the box, $8$ cubes are removed.So the total volume removed is $8cdot27=216$ .Therefore, the desired percentage is $frac{216}{1200}cdot100 = boxed{mathrm{(D)} 18%}$
Since she walked $1$ km to school and $1$ km back home, her total distance is $1+1=2$ km.Since she spent $30$ minutes walking to school and $10$ minutes walking back home, her total time is $30+10=40$ minutes = $frac{40}{60}=frac{2}{3}$ hours.Therefore her average speed in km/hr is $frac{2}{frac{2}{3}}=boxed{mathrm{(A)} 3}$ .The average speed of two speeds that travel the same distance is the harmonic mean of the speeds, or $dfrac{2}{dfrac{1}{x}+dfrac{1}{y}}=dfrac{2xy}{x+y}$ (for speeds $x$ and $y$ ). Mary's speed going to school is $2,text{km/hr}$ , and her speed coming back is $6,text{km/hr}$ . Plugging the numbers in, we get that the average speed is $dfrac{2times 6times 2}{6+2}=dfrac{24}{8}=boxed{mathrm{(A)} 3}$ .
Using factoring: $2x^{2}+3x-5=0$ $(2x+5)(x-1)=0$ $x = -frac{5}{2}$ or $x=1$ So $d$ and $e$ are $-frac{5}{2}$ and $1$ .Therefore the answer is $left(-frac{5}{2}-1right)(1-1)=left(-frac{7}{2}right)(0)=boxed{mathrm{(B)} 0}$
We can use the sum and product of a quadratic:

$(d-1)(e-1)=de-(d+e)+1 impliestext{product}-text{sum}+1 implies dfrac{c}{a}-left(-dfrac{b}{a}right)+1 implies dfrac{b+c}{a}+1= dfrac{5}{-5}+1=boxed{mathrm{(B)} 0}$
Examining statement C: $x heartsuit 0 = |x-0| = |x|$ $|x| neq x$ when $x<0$ , but statement C says that it does for all $x$ .Therefore the statement that is not true is $boxed{mathrm{(C)} xheartsuit 0=x text{for all} x}$
By the triangle inequality, no side may have a length greater than the semiperimeter, which is $frac{1}{2}cdot7=3.5$ .Since all sides must be integers, the largest possible length of a side is $3$ . Therefore, all such triangles must have all sides of length $1$ , $2$ , or $3$ . Since $2+2+2=6<7$ , at least one side must have a length of $3$ . Thus, the remaining two sides have a combined length of $7-3=4$ . So, the remaining sides must be either $3$ and $1$ or $2$ and $2$ . Therefore, the number of triangles is $boxed{mathrm{(B)} 2}$ .
For a positive number $n$ which is not a perfect square, exactly half of the positive factors will be less than $sqrt{n}$ .Since $60$ is not a perfect square, half of the positive factors of $60$ will be less than $sqrt{60}approx 7.746$ .Clearly, there are no positive factors of $60$ between $7$ and $sqrt{60}$ .Therefore half of the positive factors will be less than $7$ .So the answer is $boxed{mathrm{(E)} frac{1}{2}}$ .Testing all numbers less than $7$ , numbers $1, 2, 3, 4, 5$ , and $6$ divide $60$ . The prime factorization of $60$ is $2^2cdot 3 cdot 5$ . Using the formula for the number of divisors, the total number of divisors of $60$ is $(3)(2)(2) = 12$ . Therefore, our desired probability is $frac{6}{12} = boxed{mathrm{(E)} frac{1}{2}}$
$sqrt[3]{xsqrt{x}}=sqrt[3]{(sqrt{x})^{2}cdotsqrt{x}}=sqrt[3]{(sqrt{x})^{3}}=sqrt{x}$ .Therefore: $sqrt[3]{xsqrt[3]{xsqrt[3]{xsqrt{x}}}}=sqrt[3]{xsqrt[3]{xsqrt{x}}}=sqrt[3]{xsqrt{x}}= sqrt{x} Rightarrow boxed{mathrm{(A)} sqrt{x}}$ We know that $sqrt[3]{xsqrt{x}} = sqrt[3]{xcdot(x^frac{1}{2})} = sqrt[3]{x^frac{3}{2}} = x^frac{1}{2}$ We plug this into $sqrt[3]{xsqrt[3]{xsqrt[3]{xsqrt{x}}}}$ and get $sqrt[3]{xsqrt[3]{xcdot(x^frac{1}{2})}}$ . Again, we substitute and get $sqrt[3]{xcdot(x^frac{1}{2})}$ . We substitute one more time and get $x^frac{1}{2} = boxed{(A) sqrt{x}}$ .
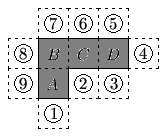Let the squares be labeled $A$ , $B$ , $C$ , and $D$ .When the polygon is folded, the "right" edge of square $A$ becomes adjacent to the "bottom edge" of square $C$ , and the "bottom" edge of square $A$ becomes adjacent to the "bottom" edge of square $D$ .So, any "new" square that is attatched to those edges will prevent the polygon from becoming a cube with one face missing.Therefore, squares $1$ , $2$ , and $3$ will prevent the polygon from becoming a cube with one face missing.Squares $4$ , $5$ , $6$ , $7$ , $8$ , and $9$ will allow the polygon to become a cube with one face missing when folded.
Thus the answer is $boxed{mathrm{(E)} 6}$ .

Another way to think of it is that a cube missing one face has $5$ of its $6$ faces. Since the shape has $4$ faces already, we need another face. The only way to add another face is if the added square does not overlap any of the others. $1$ , $2$ , and $3$ overlap, while squares $4$ to $9$ do not. The answer is $boxed{mathrm{(E)} 6}$
$AMC10+AMC12=123422$ $AMC00+AMC00=123400$ $AMC+AMC=1234$ $2cdot AMC=1234$ $AMC=frac{1234}{2}=617$ Since $A$ , $M$ , and $C$ are digits, $A=6$ , $M=1$ , $C=7$ .
Therefore, $A+M+C = 6+1+7 = boxed{mathrm{(E)} 14}$ .
The rectangle has a width of $4$ and a height of $1$ .The area of this rectangle is $4cdot1=4$ .The line $x=y$ intersects the rectangle at $(0,0)$ and $(1,1)$ .The area which $x<y$ is the right isosceles triangle with side length $1$ that has vertices at $(0,0)$ , $(1,1)$ , and $(0,1)$ .The area of this triangle is $frac{1}{2}cdot1^{2}=frac{1}{2}$ Therefore, the probability that $x<y$ is $frac{frac{1}{2}}{4}=frac{1}{8} Rightarrow boxed{mathrm{(A)} frac{1}{8}}$
Let the numbers be $x$ , $y$ , and $z$ in that order. The given tells us that $begin{eqnarray*}y&=&7z\ x&=&4(y+z)=4(7z+z)=4(8z)=32z\ x+y+z&=&32z+7z+z=40z=20\ z&=&frac{20}{40}=frac{1}{2}\ y&=&7z=7cdotfrac{1}{2}=frac{7}{2}\ x&=&32z=32cdotfrac{1}{2}=16 end{eqnarray*}$ Therefore, the product of all three numbers is $xyz=16cdotfrac{7}{2}cdotfrac{1}{2}=28 Rightarrow boxed{mathrm{(A)} 28}$ .Alternatively, we can set up the system in matrix form: $begin{eqnarray*}1x+1y+1z&=&20\ 1x-4y-4z&=&0\ 0x+1y-7z&=&0\ end{eqnarray*}$ Or, in matrix form $begin{bmatrix} 1 & 1 & 1 \ 1 & -4 & -4 \ 0 & 1 & -7 end{bmatrix} begin{bmatrix} x \ y \ z \ end{bmatrix} =begin{bmatrix} 20 \ 0 \ 0 \ end{bmatrix}$
To solve this matrix equation, we can rearrange it thus:

$begin{bmatrix} x \ y \ z \ end{bmatrix} = begin{bmatrix} 1 & 1 & 1 \ 1 & -4 & -4 \ 0 & 1 & -7 end{bmatrix} ^{-1} begin{bmatrix} 20 \ 0 \ 0 \ end{bmatrix}$

Solving this matrix equation by using inverse matrices and matrix multiplication yields

$begin{bmatrix} x \ y \ z \ end{bmatrix} = begin{bmatrix} frac{1}{2} \ frac{7}{2} \ 16 \ end{bmatrix}$

Which means that $x = frac{1}{2}$ , $y = frac{7}{2}$ , and $z = 16$ . Therefore, $xyz = frac{1}{2}cdotfrac{7}{2}cdot16 = 28 Rightarrow boxed{mathrm{(A)} 28}$
Since $d$ is a single digit prime number, the set of possible values of $d$ is ${2,3,5,7}$ .Since $e$ is a single digit prime number and is the units digit of the prime number $10d+e$ , the set of possible values of $e$ is ${3,7}$ .Using these values for $d$ and $e$ , the set of possible values of $10d+e$ is ${23,27,33,37,53,57,73,77}$ Out of this set, the prime values are ${23,37,53,73}$ Therefore the possible values of $n$ are: $2cdot3cdot23=138$
$3cdot7cdot37=777$

$5cdot3cdot53=795$

$7cdot3cdot73=1533$

The largest possible value of $n$ is $1533$ .

So, the sum of the digits of $n$ is $1+5+3+3=12 Rightarrow boxed{mathrm{(A)} 12}$
There are $100$ integers in the set.Since every $2^{text{nd}}$ integer is divisible by $2$ , there are $lfloorfrac{100}{2}rfloor=50$ integers divisible by $2$ in the set.To be divisible by both $2$ and $3$ , a number must be divisible by $(2,3)=6$ .Since every $6^{text{th}}$ integer is divisible by $6$ , there are $lfloorfrac{100}{6}rfloor=16$ integers divisible by both $2$ and $3$ in the set.So there are $50-16=34$ integers in this set that are divisible by $2$ and not divisible by $3$ .Therefore, the desired probability is $frac{34}{100}=frac{17}{50}Rightarrowboxed{mathrm{(C)} frac{17}{50}}$
$13^{2003}equiv 3^{2003}pmod{10}$ Since $3^4=81equiv1pmod{10}$ : $3^{2003}=(3^{4})^{500}cdot3^{3}equiv1^{500}cdot27equiv7pmod{10}$ Therefore, the units digit is $7 Rightarrowboxed{mathrm{(C)} 7}$
Let $s$ be the length of a side of the equilateral triangle and let $r$ be the radius of the circle.In a circle with a radius $r$ , the side of an inscribed equilateral triangle is $rsqrt{3}$ .So $s=rsqrt{3}$ .The perimeter of the triangle is $3s=3rsqrt{3}$ The area of the circle is $pi r^{2}$ So: $pi r^{2} = 3rsqrt{3}$
$pi r=3sqrt{3}$

$r=frac{3sqrt{3}}{pi} Rightarrowboxed{mathrm{(B)} frac{3sqrt{3}}{pi}}$
Multiplying both sides by $x$ : $frac{2003}{2004}x^{2}+1x+1=0$ Let the roots be $a$ and $b$ .The problem is asking for $frac{1}{a}+frac{1}{b}= frac{a+b}{ab}$ By Vieta's formulas: $a+b=(-1)^{1}frac{1}{frac{2003}{2004}}=-frac{2004}{2003}$
$ab=(-1)^{2}frac{1}{frac{2003}{2004}}=frac{2004}{2003}$

So the answer is $frac{a+b}{ab}=frac{-frac{2004}{2003}}{frac{2004}{2003}}=-1 Rightarrowboxed{mathrm{(B)} -1}$ .

Dividing both sides by $x$ ,

$frac{2003}{2004}+frac 1x+frac{1}{x^2}=0$ ,

we see by Vieta's formulas that the sum of the roots is $-1 Rightarrowboxed{mathrm{(B)} -1}$ .
$[asy] import graph; size(150); defaultpen(fontsize(8)); pair A=(-2,0), B=(2,0); filldraw(Arc((0,sqrt(3)),1,0,180)--cycle,mediumgray); fill(Arc((0,0),2,0,180)--cycle,white); draw(Arc((0,0),2,0,180)--cycle); draw((0,0)--2*expi(2*pi/6)--2*expi(2*pi/6*2)--(0,0)); label("A",(0,2),(0,4)); label("B",(0,2),(0,-1)); label("C",(0,sqrt(3)/2),(0,2)); label("1",(-0.5,sqrt(3)/2),(-1,0)); label("1",(0.5,sqrt(3)/2),(1,0)); [/asy]$ Let $[X]$ denote the area of region $X$ in the figure above.The shaded area $[A]$ is equal to the area of the smaller semicircle $[A+B]$ minus the area of a sector of the larger circle $[B+C]$ plus the area of a triangle formed by two radii of the larger semicircle and the diameter of the smaller semicircle $[C]$ .The area of the smaller semicircle is $[A+B] = frac{1}{2}picdotleft(frac{1}{2}right)^{2}=frac{1}{8}pi$ .Since the radius of the larger semicircle is equal to the diameter of the smaller semicircle, the triangle is an equilateral triangle and the sector measures $60^circ$ .The area of the $60^circ$ sector of the larger semicircle is $[B+C] = frac{60}{360}picdotleft(frac{2}{2}right)^{2}=frac{1}{6}pi$ .
The area of the triangle is $[C] = frac{1^{2}sqrt{3}}{4}=frac{sqrt{3}}{4}$ .

So the shaded area is $[A] = [A+B]-[B+C]+[C] = left(frac{1}{8}piright)-left(frac{1}{6}piright)+left(frac{sqrt{3}}{4}right)=boxed{mathrm{(C)} frac{sqrt{3}}{4}-frac{1}{24}pi}$ .
The smallest base-11 number that has 3 digits in base-10 is $100_{11}$ which is $121_{10}$ .The largest number in base-9 that has 3 digits in base-10 is $8cdot9^2+8cdot9^1+8cdot9^0=888_{9}=728_{10}$ Alternatively, you can do $9^3-1$ The smallest number in base-9 that has 3 digits in base-10 is $1cdot9^2+2cdot9^1+1cdot9^0=121_{9}=100_{10}$ Hence, all numbers that will have 3 digits in base-9, 10, and 11 will be between $728_{10}$ and $121_{10}$ , thus the total amount of numbers that will have 3 digits in base-9, 10, and 11 is $728-121+1=608$ There are 900 possible 3 digit numbers in base 10.Hence, the answer is $frac{608}{900}approx .675 approx boxed{0.7}$
Let the ordered triplet $(x,y,z)$ represent the assortment of $x$ chocolate chip cookies, $y$ oatmeal cookies, and $z$ peanut butter cookies.Using casework:Pat selects $0$ chocolate chip cookies:Pat needs to select $6-0=6$ more cookies that are either oatmeal or peanut butter.The assortments are: ${(0,6,0); (0,5,1); (0,4,2); (0,3,3); (0,2,4); (0,1,5); (0,0,6)} rightarrow 7$ assortments.Pat selects $1$ chocolate chip cookie:
Pat needs to select $6-1=5$ more cookies that are either oatmeal or peanut butter.

The assortments are: ${(1,5,0); (1,4,1); (1,3,2); (1,2,3); (1,1,4); (1,0,5) } rightarrow 6$ assortments.

Pat selects $2$ chocolate chip cookies:

Pat needs to select $6-2=4$ more cookies that are either oatmeal or peanut butter.

The assortments are: ${(2,4,0); (2,3,1); (2,2,2); (2,1,3); (2,0,4)} rightarrow 5$ assortments.

Pat selects $3$ chocolate chip cookies:

Pat needs to select $6-3=3$ more cookies that are either oatmeal or peanut butter.

The assortments are: ${(3,3,0); (3,2,1); (3,1,2); (3,0,3)} rightarrow 4$ assortments.

Pat selects $4$ chocolate chip cookies:

Pat needs to select $6-4=2$ more cookies that are either oatmeal or peanut butter.

The assortments are: ${(4,2,0); (4,1,1); (4,0,2)} rightarrow 3$ assortments.

Pat selects $5$ chocolate chip cookies:

Pat needs to select $6-5=1$ more cookies that are either oatmeal or peanut butter.

The assortments are: ${(5,1,0); (5,0,1)} rightarrow 2$ assortments.

Pat selects $6$ chocolate chip cookies:

Pat needs to select $6-6=0$ more cookies that are either oatmeal or peanut butter.

The only assortment is: ${(6,0,0)} rightarrow 1$ assortment.

The total number of assortments of cookies that can be collected is $7+6+5+4+3+2+1=28 Rightarrowboxed{mathrm{(D)} 28}$

There is a much faster way to do casework.

Case 1: 1 type of cookie - 3 ways

Case 2: 2 types of cookies - 3 ways to choose the 2 types of cookies, and 5 ways to choose how of each there are 1 and 5 2 and 4 3 and 3 4 and 2 5 and 1

$3*5=15$ cases for case 2

Case 3: 3 types of cookies - quick examination shows us that the only ways to use all three cookies are the following: 4, 1, 1: this gives us 3!/2!*1! = 3 ways 3, 2, 1: this gives us 3! = 6 ways 2, 2, 2: this gives us 1 way total of 10 cases for this case 10+15+3= $28$ total

It is given that it is possible to select at least 6 of each. Therefore, we can make a bijection to the number of ways to divide the six choices into three categories, since it is assumed that their order is unimportant. Using the ball and urns/sticks and stones/stars and bars formula, the number of ways to do this is $binom{8}{2} = 28 Rightarrowboxed{mathrm{(D)} 28}$

Suppose the six cookies to be chosen are the stars, as we attempt to implement stars and bars. We take two dividers, and place them between the cookies, such that the six cookies are split into 3 groups, where the groups are the number of chocolate chip, oatmeal, and peanut butter cookies, and each group can have 0. First, assume that the two dividers cannot go in between the same two cookies. By stars and bars, there are $dbinom{7}{2}$ ways to make the groups.

Finally, since the two dividers can be together, we must add those cases where the two dividers are in the same space between cookies. There are 7 spaces, and hence 7 cases.

Our final answer is $21+7=boxed{mathrm{(D)} 28}$
$angle GHC = angle AHB$ (Vertical angles are equal). $angle F = angle B$ (Both are 90 degrees). $angle BHA = angle HAD$ (Alt. Interior Angles are congruent).Therefore $triangle GFA$ and $triangle ABH$ are similar. $triangle GCH$ and $triangle GEA$ are also similar. $DA$ is 9, therefore $EA$ must equal 5. Similarly, $CH$ must equal 3.Because $GCH$ and $GEA$ are similar, the ratio of $CH; =; 3$ and $EA; =; 5$ , must also hold true for $GH$ and $HA$ . $frac{GH}{GA} = frac{3}{5}$ , so $HA$ is $frac{2}{5}$ of $GA$ . By Pythagorean theorem, $(HA)^2; =; (HB)^2; +; (BA)^2;...;HA=10$ .
$HA: =: 10 =: frac{2}{5}*(GA)$ .

$GA: =: 25.$

So $frac{GA}{HA}: =: frac{GF}{BA}$ .

$frac{25}{10}: =: frac{GF}{8}$ .

Therefore $GF= boxed{mathrm{(B)} 20}$ .

Since $ABCD$ is a rectangle, $CD=AB=8$ .

Since $ABCD$ is a rectangle and $GF perp AF$ , $angle GFE = angle CDE = angle ABC = 90^circ$ .

Since $ABCD$ is a rectangle, $AD || BC$ .

So, $AH$ is a transversal, and $angle GAF = angle AHB$ .

This is sufficient to prove that $GFE approx CDE$ and $GFA approx ABH$ .

Using ratios:

$frac{GF}{FE}=frac{CD}{DE}$

$frac{GF}{FD+4}=frac{8}{4}=2$

$GF=2 cdot (FD+4)=2 cdot FD+8$

$frac{GF}{FA}=frac{AB}{BH}$

$frac{GF}{FD+9}=frac{8}{6}=frac{4}{3}$

$GF=frac{4}{3} cdot (FD+9)=frac{4}{3} cdot FD+12$

Since $GF$ can't have 2 different lengths, both expressions for $GF$ must be equal.

$2 cdot FD+8=frac{4}{3} cdot FD+12$

$frac{2}{3} cdot FD=4$

$FD=6$

$GF=2 cdot FD+8=2cdot6+8=boxed{mathrm{(B)} 20}$

Since $ABCD$ is a rectangle, $CH=3$ , $EA=5$ , and $CD=8$ . From the Pythagorean Theorem, $CE^2=CD^2+DE^2=80Rightarrow CE=4sqrt{5}$ .

Lemma

Statement: $GCH approx GEA$

Proof: $angle CGH=angle EGA$ , obviously.

$begin{eqnarray*} angle HCE&=&180^{circ}-angle CHG\ angle DCE&=&angle CHG-90^{circ}\ angle CEED&=&180-angle CHG\ angle GEA&=&angle GCH end{eqnarray*}$

Since two angles of the triangles are equal, the third angles must equal each other. Therefore, the triangles are similar.

Let $GC=x$ .

$begin{eqnarray*} dfrac{x}{3}&=&dfrac{x+4sqrt{5}}{5}\ 5x&=&3x+12sqrt{5}\ 2x&=&12sqrt{5}\ x&=&6sqrt{5} end{eqnarray*}$

Also, $triangle GFEapprox triangle CDE$ , therefore

$[dfrac{8}{4sqrt{5}}=dfrac{GF}{10sqrt{5}}]$

We can multiply both sides by $sqrt{5}$ to get that $GF$ is twice of 10, or $boxed{mathrm{(B)} 20}$

We extend $BC$ such that it intersects $GF$ at $X$ . Since $ABCD$ is a rectangle, it follows that $CD=8$ , therefore, $XF=8$ . Let $GX=y$ . From the similarity of triangles $GCH$ and $GEA$ , we have the ratio $3:5$ (as $CH=9-6=3$ , and $EA=9-4=5$ ). $GX$ and $GF$ are the altitudes of $GCH$ and $GEA$ , respectively. Thus, $y:y+8 = 3:5$ , from which we have $y=12$ , thus $GF=y+8=12+8=boxed{mathrm{(B)} 20}$

Since $GFperp AF$ and $AFperp CD,$ we have $GFparallel CDparallel AB.$ Thus, $triangle CDEsim GFE.$ Suppose $GF=x$ and $FD=y.$ Thus, we have $dfrac{x}{8}=dfrac{y+4}{4}.$ Additionally, now note that $triangle GAFsim AHB,$ which is pretty obvious from insight, but can be proven by AA with extending $BH$ to meet $GF.$ From this new pair of similar triangles, we have $dfrac{x}{8}=dfrac{y+9}{6}.$ Therefore, we have by combining those two equations, $[dfrac{y+9}{6}=dfrac{y+4}{4}.]$ Solving, we have $y=6,$ and therefore $x=boxed{mathrm{(B)} 20}$
There are $1+3+5+...+2003=1002^{2}=1004004$ small equilateral triangles.Each small equilateral triangle needs $3$ toothpicks to make it.But, each toothpick that isn't one of the $1002cdot3=3006$ toothpicks on the outside of the large equilateral triangle is a side for $2$ small equilateral triangles.So, the number of toothpicks on the inside of the large equilateral triangle is $frac{10040004cdot3-3006}{2}=1504503$ Therefore the total number of toothpicks is $1504503+3006=boxed{mathrm{(C)} 1,507,509}$ We see that the bottom row of $2003$ small triangles are formed from $1002$ upward-facing triangles and $1001$ downward-facing triangles. Since each upward-facing triangle uses three distinct toothpicks, and since the total number of upward-facing triangles is $1002+1001+...+1=frac{1003cdot1002}{2}=502503$ , we have that the total number of toothpicks is $3cdot 502503=boxed{mathrm{(C)} 1,507,509}$
Experimenting a bit we find that the number of toothpicks needs a triangle with $1$ , $2$ and $3$ rows is $1cdot{3}$ , $3cdot{3}$ and $6cdot{3}$ respectively. Since $1$ , $3$ and $6$ are triangular numbers we know that depending on how many rows there are in the triangle, the number we multiply by $3$ to find total no.toothpicks is the corresponding triangular number. Since the triangle in question has $2n-1=2003implies{n=1002}$ rows, we can use $frac{n(n+1)}{2}$ to find the triangular number for that row and multiply by $3$ , hence finding the total no.toothpicks; this is just $frac{3cdot{1002}cdot{1003}}{2}=3cdot{501}cdot{1003}=boxed{mathrm{(C)} 1,507,509}$ .
Let $R_i$ and $B_j$ designate the red card numbered $i$ and the blue card numbered $j$ , respectively. $B_5$ is the only blue card that $R_5$ evenly divides, so $R_5$ must be at one end of the stack and $B_5$ must be the card next to it. $R_1$ is the only other red card that evenly divides $B_5$ , so $R_1$ must be the other card next to $B_5$ . $B_4$ is the only blue card that $R_4$ evenly divides, so $R_4$ must be at one end of the stack and $B_4$ must be the card next to it. $R_2$ is the only other red card that evenly divides $B_4$ , so $R_2$ must be the other card next to $B_4$ . $R_2$ doesn't evenly divide $B_3$ , so $B_3$ must be next to $R_1$ , $B_6$ must be next to $R_2$ , and $R_3$ must be in the middle.
This yields the following arrangement from top to bottom: ${R_5,B_5,R_1,B_3,R_3,B_6,R_2,B_4,R_4}$

Therefore, the sum of the numbers on the middle three cards is $3+3+6=boxed{mathrm{(E)} 12}$ .
$11|q+r$ implies that $11|100q+r$ , so $11|n$ . Then, $n$ can range from $10010$ to $99990$ for a total of $boxed{8181Rightarrow mathrm{(B)}}$ numbers.When a $5$ -digit number is divided by $100$ , the first $3$ digits become the quotient, $q$ , and the last $2$ digits become the remainder, $r$ .Therefore, $q$ can be any integer from $100$ to $999$ inclusive, and $r$ can be any integer from $0$ to $99$ inclusive.For each of the $9cdot10cdot10=900$ possible values of $q$ , there are at least $leftlfloor frac{100}{11} rightrfloor = 9$ possible values of $r$ such that $q+r equiv 0pmod{11}$ .Since there is $1$ "extra" possible value of $r$ that is congruent to $0pmod{11}$ , each of the $leftlfloor frac{900}{11} rightrfloor = 81$ values of $q$ that are congruent to $0pmod{11}$ have $1$ more possible value of $r$ such that $q+r equiv 0pmod{11}$ .Therefore, the number of possible values of $n$ such that $q+r equiv 0pmod{11}$ is $900cdot9+81cdot1=8181 Rightarrow B$ .
Let $n$ equal $overline{abcde}$ , where $a$ through $e$ are digits. Therefore,

$q=overline{abc}=100a+10b+c$

$r=overline{de}=10d+e$

We now take $q+rbmod{11}$ :

$q+r=100a+10b+c+10d+eequiv a-b+c-d+eequiv 0bmod{11}$

The divisor trick for 11 is as follows:

"Let $n=overline{a_1a_2a_3cdots a_x}$ be an $x$ digit integer. If $a_1-a_2+a_3-cdots +(-1)^{x-1} a_x$ is divisible by $11$ , then $n$ is also divisible by $11$ ."

Therefore, the five digit number $n$ is divisible by 11. The 5-digit multiples of 11 range from $910cdot 11$ to $9090cdot 11$ . There are $8181Rightarrow mathrm{(B)}$ divisors of 11 between those inclusive.

Since $q$ is a quotient and $r$ is a remainder when $n$ is divided by $100$ . So we have $n=100q+r$ . Since we are counting choices where $q+r$ is divisible by $11$ , we have $n=99q+q+r=99q+11k$ for some $k$ . This means that $n$ is the sum of two multiples of $11$ and would thus itself be a multiple of $11$ . Then we can count all the five digit multiples of $11$ as in Solution 2. (This solution is essentially the same as Solution 2, but it does not necessarily involve mods and so could potentially be faster.)