Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2004 AMC12A 真题及答案详细解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月5日上午11:46

2004 AMC 12A 真题

答案详细解析请参考文末

Problem 1

Alicia earns $20$ dollars per hour, of which $1.45%$ is deducted to pay local taxes. How many cents per hour of Alicia's wages are used to pay local taxes?

$mathrm {(A)} 0.0029 qquad mathrm {(B)} 0.029 qquad mathrm {(C)} 0.29 qquad mathrm {(D)} 2.9 qquad mathrm {(E)} 29$

Problem 2

On the AMC 12, each correct answer is worth $6$ points, each incorrect answer is worth $0$ points, and each problem left unanswered is worth $2.5$ points. If Charlyn leaves $8$ of the $25$ problems unanswered, how many of the remaining problems must she answer correctly in order to score at least $100$ ?

$mathrm {(A)} 11 qquad mathrm {(B)} 13 qquad mathrm {(C)} 14 qquad mathrm {(D)} 16 qquad mathrm {(E)} 17$

Problem 3

For how many ordered pairs of positive integers $(x,y)$ is $x+2y=100$ ?

$mathrm {(A)} 33 qquad mathrm {(B)} 49 qquad mathrm {(C)} 50 qquad mathrm {(D)} 99 qquad mathrm {(E)} 100$

Problem 4

Bertha has $6$ daughters and no sons. Some of her daughters have $6$ daughters, and the rest have none. Bertha has a total of $30$ daughters and granddaughters, and no great-granddaughters. How many of Bertha's daughters and grand-daughters have no children?

$mathrm {(A)} 22 qquad mathrm {(B)} 23 qquad mathrm {(C)} 24 qquad mathrm {(D)} 25 qquad mathrm {(E)} 26$

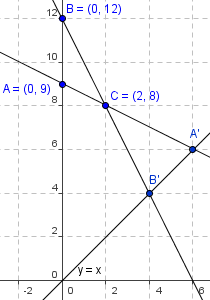
Problem 5

The graph of the line $y=mx+b$ is shown. Which of the following is true?

2004 AMC 12A Problem 5.png

$mathrm {(A)} mb<-1 qquad mathrm {(B)} -1<mb<0 qquad mathrm {(C)} mb=0 qquad mathrm {(D)} 0<mb<1 qquad mathrm {(E)} mb>1$

Problem 6

Let $U=2cdot 2004^{2005}$ , $V=2004^{2005}$ , $W=2003cdot 2004^{2004}$ , $X=2cdot 2004^{2004}$ , $Y=2004^{2004}$ and $Z=2004^{2003}$ . Which of the following is the largest?

$mathrm {(A)} U-V qquad mathrm {(B)} V-W qquad mathrm {(C)} W-X qquad mathrm {(D)} X-Y qquad mathrm {(E)} Y-Z qquad$

Problem 7

A game is played with tokens according to the following rules. In each round, the player with the most tokens gives one token to each of the other players and also places one token into a discard pile. The game ends when some player runs out of tokens. Players $A$ , $B$ and $C$ start with $15$ , $14$ and $13$ tokens, respectively. How many rounds will there be in the game?

$mathrm {(A)} 36 qquad mathrm {(B)} 37 qquad mathrm {(C)} 38 qquad mathrm {(D)} 39 qquad mathrm {(E)} 40 qquad$

Problem 8

In the overlapping triangles $triangle{ABC}$ and $triangle{ABE}$ sharing common side $AB$ , $angle{EAB}$ and $angle{ABC}$ are right angles, $AB=4$ , $BC=6$ , $AE=8$ , and $overline{AC}$ and $overline{BE}$ intersect at $D$ . What is the difference between the areas of $triangle{ADE}$ and $triangle{BDC}$ ?

$mathrm {(A)} 2 qquad mathrm {(B)} 4 qquad mathrm {(C)} 5 qquad mathrm {(D)} 8 qquad mathrm {(E)} 9 qquad$ $[asy] size(150); defaultpen(linewidth(0.4)); //Variable Declarations pair A, B, C, D, E; //Variable Definitions A=(0, 0); B=(4, 0); C=(4, 6); E=(0, 8); D=extension(A,C,B,E); //Initial Diagram draw(A--B--C--A--E--B); label("$A$",A,SW); label("$B$",B,SE); label("$C$",C,NE); label("$D$",D,3N); label("$E$",E,NW); //Side labels label("$4$",A--B,S); label("$8$",A--E,W); label("$6$",B--C,ENE); [/asy]$

Problem 9

A company sells peanut butter in cylindrical jars. Marketing research suggests that using wider jars would increase sales. If the diameter of the jars is increased by $25%$ without altering the volume, by what percent must the height be decreased?

$text {(A)} 10% qquad text {(B)} 25% qquad text {(C)} 36% qquad text {(D)} 50% qquad text {(E)}60%$

Problem 10

The sum of $49$ consecutive integers is $7^5$ . What is their median?

$text {(A)} 7 qquad text {(B)} 7^2qquad text {(C)} 7^3qquad text {(D)} 7^4qquad text {(E)}7^5$

Problem 11

The average value of all the pennies, nickels, dimes, and quarters in Paula's purse is $20$ cents. If she had one more quarter, the average value would be $21$ cents. How many dimes does she have in her purse?

$text {(A)}0 qquad text {(B)} 1 qquad text {(C)} 2 qquad text {(D)} 3qquad text {(E)}4$

Problem 12

Let $A = (0,9)$ and $B = (0,12)$ . Points $A'$ and $B'$ are on the line $y = x$ , and $overline{AA'}$ and $overline{BB'}$ intersect at $C = (2,8)$ . What is the length of $overline{A'B'}$ ?

$text {(A)} 2 qquad text {(B)} 2sqrt2 qquad text {(C)} 3 qquad text {(D)} 2 + sqrt 2qquad text {(E)}3sqrt 2$

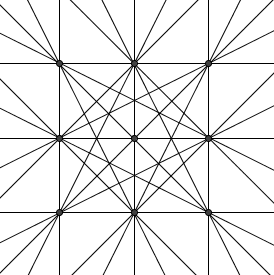
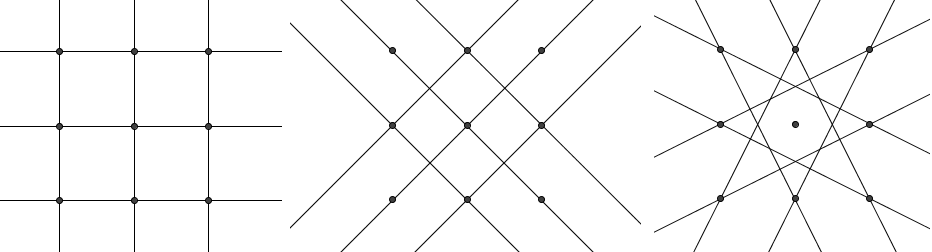
Problem 13

Let $S$ be the set of points $(a,b)$ in the coordinate plane, where each of $a$ and $b$ may be $- 1$ , $0$ , or $1$ . How many distinct lines pass through at least two members of $S$ ?

$text {(A)} 8 qquad text {(B)} 20 qquad text {(C)} 24 qquad text {(D)} 27qquad text {(E)}36$

Problem 14

A sequence of three real numbers forms an arithmetic progression with a first term of $9$ . If $2$ is added to the second term and $20$ is added to the third term, the three resulting numbers form a geometric progression. What is the smallest possible value for the third term in the geometric progression?

$text {(A)} 1 qquad text {(B)} 4 qquad text {(C)} 36 qquad text {(D)} 49 qquad text {(E)}81$

Problem 15

Brenda and Sally run in opposite directions on a circular track, starting at diametrically opposite points. They first meet after Brenda has run $100$ meters. They next meet after Sally has run $150$ meters past their first meeting point. Each girl runs at a constant speed. What is the length of the track in meters?

$text {(A)}250 qquad text {(B)}300 qquad text {(C)}350 qquad text {(D)} 400qquad text {(E)}500$

Problem 16

The set of all real numbers $x$ for which

$[log_{2004}(log_{2003}(log_{2002}(log_{2001}{x})))]$

is defined is ${x|x > c}$ . What is the value of $c$ ?

$text {(A)} 0qquad text {(B)}2001^{2002} qquad text {(C)}2002^{2003} qquad text {(D)}2003^{2004} qquad text {(E)}2001^{2002^{2003}}$

Problem 17

Let $f$ be a function with the following properties:

$(i) f(1) = 1$ , and

$(ii) f(2n) = ntimes f(n)$ , for any positive integer $n$ .

What is the value of $f(2^{100})$ ?

$text {(A)} 1 qquad text {(B)} 2^{99} qquad text {(C)} 2^{100} qquad text {(D)} 2^{4950} qquad text {(E)}2^{9999}$

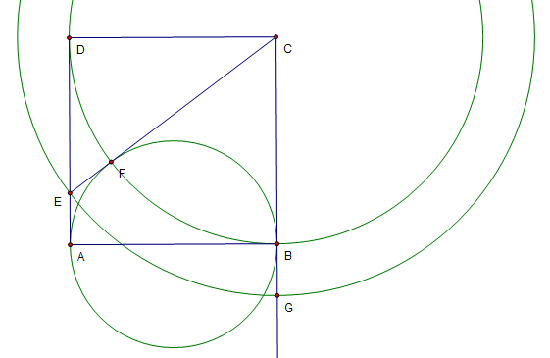
Problem 18

Square $ABCD$ has side length $2$ . A semicircle with diameter $overline{AB}$ is constructed inside the square, and the tangent to the semicircle from $C$ intersects side $overline{AD}$ at $E$ . What is the length of $overline{CE}$ ?

$[asy] size(100); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180)); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); [/asy]$

$text {(A)} frac {2 + sqrt5}{2} qquad text {(B)} sqrt 5 qquad text {(C)} sqrt 6 qquad text {(D)} frac52 qquad text {(E)}5 - sqrt5$

Problem 19

Circles $A, B$ and $C$ are externally tangent to each other, and internally tangent to circle $D$ . Circles $B$ and $C$ are congruent. Circle $A$ has radius $1$ and passes through the center of $D$ . What is the radius of circle $B$ ?

$text {(A)} frac23 qquad text {(B)} frac {sqrt3}{2} qquad text {(C)}frac78 qquad text {(D)}frac89 qquad text {(E)}frac {1 + sqrt3}{3}$

Problem 20

Select numbers $a$ and $b$ between $0$ and $1$ independently and at random, and let $c$ be their sum. Let $A, B$ and $C$ be the results when $a, b$ and $c$ , respectively, are rounded to the nearest integer. What is the probability that $A + B = C$ ?

$text {(A)} frac14 qquad text {(B)} frac13 qquad text {(C)} frac12 qquad text {(D)} frac23 qquad text {(E)}frac34$

Problem 21

If $sum_{n = 0}^{infty}cos^{2n}theta = 5$ , what is the value of $cos{2theta}$ ?

$text {(A)} frac15 qquad text {(B)} frac25 qquad text {(C)} frac {sqrt5}{5}qquad text {(D)} frac35 qquad text {(E)}frac45$

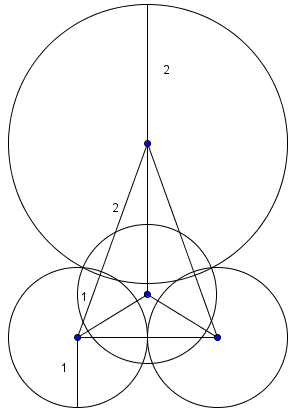
Problem 22

Three mutually tangent spheres of radius $1$ rest on a horizontal plane. A sphere of radius $2$ rests on them. What is the distance from the plane to the top of the larger sphere?

$text {(A)} 3 + frac {sqrt {30}}{2} qquad text {(B)} 3 + frac {sqrt {69}}{3} qquad text {(C)} 3 + frac {sqrt {123}}{4}qquad text {(D)} frac {52}{9}qquad text {(E)}3 + 2sqrt2$

Problem 23

A polynomial

$[P(x) = c_{2004}x^{2004} + c_{2003}x^{2003} + ... + c_1x + c_0]$

has real coefficients with $c_{2004}not = 0$ and $2004$ distinct complex zeroes $z_k = a_k + b_ki$ , $1leq kleq 2004$ with $a_k$ and $b_k$ real, $a_1 = b_1 = 0$ , and

$[sum_{k = 1}^{2004}{a_k} = sum_{k = 1}^{2004}{b_k}.]$

Which of the following quantities can be a nonzero number?

$text {(A)} c_0 qquad text {(B)} c_{2003} qquad text {(C)} b_2b_3...b_{2004} qquad text {(D)} sum_{k = 1}^{2004}{a_k} qquad text {(E)}sum_{k = 1}^{2004}{c_k}$

Problem 24

A plane contains points $A$ and $B$ with $AB = 1$ . Let $S$ be the union of all disks of radius $1$ in the plane that cover $overline{AB}$ . What is the area of $S$ ?

$text {(A)} 2pi + sqrt3 qquad text {(B)} frac {8pi}{3} qquad text {(C)} 3pi - frac {sqrt3}{2} qquad text {(D)} frac {10pi}{3} - sqrt3 qquad text {(E)}4pi - 2sqrt3$

Problem 25

For each integer $ngeq 4$ , let $a_n$ denote the base- $n$ number $0.overline{133}_n$ . The product $a_4a_5...a_{99}$ can be expressed as $frac {m}{n!}$ , where $m$ and $n$ are positive integers and $n$ is as small as possible. What is the value of $m$ ?

$text {(A)} 98 qquad text {(B)} 101 qquad text {(C)} 132qquad text {(D)} 798qquad text {(E)}962$

2004 AMC12 A 真题答案详细解析

$20$ dollars is the same as $2000$ cents, and $1.45%$ of $2000$ is $0.0145times2000=29$ cents. $Rightarrowboxed{mathrm{(E)} 29}$ .
She gets $8*2.5=20$ points for the problems she didn't answer. She must get $leftlceil frac{100-20}{6} rightrceil =14 Rightarrow text {(C)}$ problems right to score at least 100.
Solution 1

Every integer value of $y$ leads to an integer solution for $x$ Since $y$ must be positive, $ygeq 1$

Also, $y = frac{100-x}{2}$ Since $x$ must be positive, $y < 50$

$1 leq y < 50$ This leaves $49$ values for y, which mean there are $49$ solutions to the equation $Rightarrow mathrm{(B)}$

Solution 2

If $x$ and $2y$ must each be positive integers, then we can say that $x$ is at least 1 and $2y$ is at least 1. From there, we want to find out how many ways there are to distribute the other 98 ones (the smallest positive integer addends of 100). 98 identical objects can be distributed to two distinct bins in 99 ways (think stars and bars), yet this 99 is an overcount. Because $y$ must be an integer, $2y$ must be even; thus only 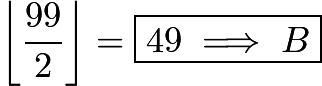$leftlfloor frac{99}{2} rightrfloor = boxed{ 49 implies B}$ ways exist to distribute these ones.
Solution

Since Bertha has $6$ daughters, she has $30-6=24$ granddaughters, of which none have daughters. Of Bertha's daughters, $frac{24}6=4$ have daughters, so $6-4=2$ do not have daughters. Therefore, of Bertha's daughters and granddaughters, $24+2=26$ do not have daughters. $boxed{mathrm{(E)} 26}$
- - Alcumus**
Bertha has $30 - 6 = 24$ granddaughters, none of whom have any daughters. The granddaughters are the children of $24/6 = 4$ of Bertha's daughters, so the number of women having no daughters is $30 - 4 = boxed{26}$ .

Solution 2

Draw a tree diagram and see that the answer can be found in the sum of $6+6$ granddaughters, $5+5$ daughters, and $4$ more daughters. Adding them together gives the answer of $boxed{mathrm{(E)} 26}$ .
The line appears to have a slope of $-dfrac{1}{2}$ and y-intercept of $dfrac{4}{5}$ up. $dfrac{4}{5}cdot dfrac{-1}{2}=dfrac{-4}{10} Rightarrow mathrm {(B)}$
$begin{eqnarray*} U-V&=&2004*2004^{2004}\ V-W&=&1*2004^{2004}\ W-X&=&2001*2004^{2004}\ X-Y&=&1*2004^{2004}\ Y-Z&=&2003*2004^{2003} end{eqnarray*}$ After comparison, $U-V$ is the largest. $mathrm {(A)}$
We look at a set of three rounds, where the players begin with $x+1$ , $x$ , and $x-1$ tokens. After three rounds, there will be a net loss of $1$ token per player (they receive two tokens and lose three). Therefore, after $36$ rounds -- or $12$ three-round sets, $A,B$ and $C$ will have $3$ , $2$ , and $1$ tokens, respectively. After $1$ more round, player $A$ will give away $3$ tokens, leaving it empty-handed, and thus the game will end. We then have there are $36+1=boxed{mathrm{(B)} 37}$ rounds until the game ends.
Solution 1

Since $AE perp AB$ and $BC perp AB$ , $AE parallel BC$ . By alternate interior angles and $AAsim$ , we find that $triangle ADE sim triangle CDB$ , with side length ratio $frac{4}{3}$ . Their heights also have the same ratio, and since the two heights add up to $4$ , we have that $h_{ADE} = 4 cdot frac{4}{7} = frac{16}{7}$ and $h_{CDB} = 3 cdot frac 47 = frac {12}7$ . Subtracting the areas, $frac{1}{2} cdot 8 cdot frac {16}7 - frac 12 cdot 6 cdot frac{12}7 = 4$ $Rightarrow$ $boxed{mathrm{(B)} 4}$ .

Solution 2

Let $[X]$ represent the area of figure $X$ . Note that $[triangle BEA]=[triangle ABD]+[triangle ADE]$ and $[triangle BCA]=[triangle ABD]+[triangle BDC]$ .

$[triangle ADE]-[triangle BDC]=[triangle BEA]-[triangle BCA]=frac{1}{2}times8times4-frac{1}{2}times6times4= 16-12=4Rightarrowboxed{mathrm{(B)} 4}$

Solution 3

Put figure $ABCDE$ on a graph. $overline{AC}$ goes from (0, 0) to (4, 6) and $overline{BE}$ goes from (4, 0) to (0, 8). $overline{AC}$ is on line $y = 1.5x$ . $overline{BE}$ is on line $y = -2x + 8$ . Finding intersection between these points,

$1.5x = -2x + 8$ .

$3.5x = 8$

$x = 8 times frac{2}{7}$

$= frac{16}{7}$

This gives us the x-coordinate of D. So, $frac{16}{7}$ is the height of $triangle ADE$ , then area of $triangle ADE$ is $frac{16}{7} times 8 times frac{1}{2}$ $= frac{64}{7}$

Now, the height of $triangle BDC$ is $4-frac{16}{7} = frac{12}{7}$ And the area of $triangle BDC$ is $6 times frac{12}{7} times frac{1}{2} = frac{36}{7}$

This gives us $frac{64}{7} - frac{36}{7} = 4$

Therefore, the difference is $4$
When the diameter is increased by $25%$ , it is increased by $dfrac{5}{4}$ , so the area of the base is increased by $left(dfrac54right)^2=dfrac{25}{16}$ .To keep the volume the same, the height must be $dfrac{1}{frac{25}{16}}=dfrac{16}{25}$ of the original height, which is a $36%$ reduction. $boxed{mathrm{(C)} 36}$
The median of a sequence is the middle number of the sequence when the sequence is arranged in order. Since the integers are consecutive, the median is also the mean, so the median is $frac{7^5}{49} = 7^3 mathrm{(C)}$ .
Solution 1

Let the total value, in cents, of the coins Paula has originally be $v$ , and the number of coins she has be $n$ . Then $frac{v}{n}=20Longrightarrow v=20n$ and $frac{v+25}{n+1}=21$ . Substituting yields: $20n+25=21(n+1),$ so $n=4$ , $v = 80.$ Then, we see that the only way Paula can satisfy this rule is if she had $3$ quarters and $1$ nickel in her purse. Thus, she has $boxed{mathrm{(A)} 0}$ dimes.

Solution 2

If the new coin was worth $20$ cents, adding it would not change the mean. The additional $5$ cents raise the mean by $1$ , thus the new number of coins must be $5$ . Therefore there were $4$ coins worth a total of $4times20=80$ cents. As in the previous solution, we conclude that the only way to get $80$ cents using $4$ coins is $25+25+25+5$ . Thus, having three quarters, one nickel, and no dimes $boxed{mathrm{(A)} 0}$
The equation of $overline{AA'}$ can be found using points $A, C$ to be $y - 9 = left(frac{9-8}{0-2}right)(x - 0) Longrightarrow y = -frac{1}{2}x + 9$ . Similarily, $overline{BB'}$ has the equation $y - 12 = left(frac{12-8}{0-2}right)(x-0) Longrightarrow y = -2x + 12$ . These two equations intersect the line $y=x$ at $(6,6)$ and $(4,4)$ . Using the distance formula or $2004 AMC12A 真题及答案详细解析$ right triangles, the answer is $2sqrt{2} mathrm{(B)}$ .
Solution 1

Let's count them by cases:
- Case 1: The line is horizontal or vertical, clearly $3 cdot 2 = 6$ .
- Case 2: The line has slope $pm 1$ , with $2$ through $(0,0)$ and $4$ additional ones one unit above or below those. These total $6$ .
- Case 3: The only remaining lines pass through two points, a vertex and a non-vertex point on the opposite side. Thus we have each vertex pairing up with two points on the two opposites sides, giving $4 cdot 2 = 8$ lines.
These add up to $6+6+8=20 mathrm{(B)}$ .

Solution 2

There are ${9 choose 2} = 36$ ways to pick two points, but we've clearly overcounted all of the lines which pass through three points. In fact, each line which passes through three points will have been counted ${3 choose 2} = 3$ times, so we have to subtract $2$ for each of these lines. Quick counting yields $3$ horizontal, $3$ vertical, and $2$ diagonal lines, so the answer is $36 - 2(3+3+2) = 20$ distinct lines.

Solution 3

First consider how many lines go through $(-1, -1)$ and hit two points in $S$ . You can see that there are $5$ such lines. Now, we cross out $(-1, -1)$ and make sure to never consider consider lines that go through it anymore (As doing so would be double counting). Repeat for $(-1, 0)$ , making sure not to count the vertical line as it goes through the crossed out $(-1, -1)$ . Then cross out $(-1, 0)$ . Repeat for the rest, and count $20$ lines in total.
Solution 1

Let $d$ be the common difference. Then $9$ , $9+d+2=11+d$ , $9+2d+20=29+2d$ are the terms of the geometric progression. Since the middle term is the geometric mean of the other two terms, $(11+d)^2 = 9(2d+29)$ $Longrightarrow d^2 + 4d - 140$ $= (d+14)(d-10) = 0$ . The smallest possible value occurs when $d = -14$ , and the third term is $2(-14) + 29 = 1Rightarrowboxed{mathrm{(A)} 1}$ .

Solution 2

Let $d$ be the common difference and $r$ be the common ratio. Then the arithmetic sequence is $9$ , $9+d$ , and $9+2d$ . The geometric sequence (when expressed in terms of $d$ ) has the terms $9$ , $11+d$ , and $29+2d$ . Thus, we get the following equations:

$9r=11+dRightarrow d=9r-11$

$9r^2=29+2d$

Plugging in the first equation into the second, our equation becomes $9r^2=29+18r-22Longrightarrow9r^2-18r-7=0$ . By the quadratic formula, $r$ can either be $-frac{1}{3}$ or $frac{7}{3}$ . If $r$ is $-frac{1}{3}$ , the third term (of the geometric sequence) would be $1$ , and if $r$ is $frac{7}{3}$ , the third term would be $49$ . Clearly the minimum possible value for the third term of the geometric sequence is $boxed{mathrm{(A)} 1}$ .

Solution 3

Let the three numbers be, in increasing order, $z,y,9$

Hence, we have that $9-y=y-zimplies 9+z=2y$ .

Also, from the second part of information given, we get that

$frac{9}{y+2}=frac{y+2}{z+20}implies 9(z+20)=(y+2)^2implies y=3(sqrt{z+20})-2$

Plugging back in..

$9+z=6(sqrt{z+20})-4implies (9+z)^2=36(z+20)$

Simplifying, we get that $z^2-10z-551=0$

Applying the quadratic formula, we get that $z=frac{10pm sqrt{2304}}{2}implies frac{10pm48}{2}$

Obviously, in order to minimize the value of $z$ , we have to subtract. Hence, $z=-19$

However, the problem asks for the minimum value of the third term in a geometric progression.

Hence, the answer is $-19+20=boxed{1} implies boxed{A}$
Solution 1

Call the length of the race track $x$ . When they meet at the first meeting point, Brenda has run $100$ meters, while Sally has run $frac{x}{2} - 100$ meters. By the second meeting point, Sally has run $150$ meters, while Brenda has run $x - 150$ meters. Since they run at a constant speed, we can set up a proportion: $frac{100}{x- 150} = frac{frac{x}{2} - 100}{150}$ . Cross-multiplying, we get that $x = 350Longrightarrowboxed{mathrm{(C)} 350}$ .

Sidenote by carlos8:

Since they run at constant speeds, Brenda must've ran 200 meters to get to the second meeting point, therefore we can make an equation $200 = x-150$ , solving for $x$ , gives us our answer $350$ .

Solution 2

The total distance the girls run between the start and the first meeting is one half of the track length. The total distance they run between the two meetings is the track length. As the girls run at constant speeds, the interval between the meetings is twice as long as the interval between the start and the first meeting. Thus between the meetings Brenda will run $2times100=200$ meters. Therefore the length of the track is $150 + 200 = 350$ meters $Rightarrowboxed{mathrm{(C)} 350}$
We know that the domain of $log_k n$ , where $k$ is a constant, is $n > 0$ . So $log_{2003}(log_{2002}(log_{2001}{x})) > 0$ . By the definition of logarithms, we then have $log_{2002}(log_{2001}{x})) > 2003^0 = 1$ . Then $log_{2001}{x} > 2002^1 = 2002$ and $x > 2001^{2002} mathrm{(B)}$ .
$f(2^{100}) = f(2 times 2^{99}) = 2^{99} times f(2^{99})$ $= 2^{99} cdot 2^{98} times f(2^{98}) = ldots$ $= 2^{99}2^{98}cdots 2^{1} cdot 1 cdot f(1)$ $= 2^{99 + 98 + ldots + 2 + 1}$ $= 2^{frac{99(100)}{2}} = 2^{4950}$ $Rightarrow mathrm{(D)}$ .
Solution 1

$[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2; draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); [/asy]$

Let the point of tangency be $F$ . By the Two Tangent Theorem $BC = FC = 2$ and $AE = EF = x$ . Thus $DE = 2-x$ . The Pythagorean Theorem on $triangle CDE$ yields

$begin{align*} DE^2 + CD^2 &= CE^2\ (2-x)^2 + 2^2 &= (2+x)^2\ x^2 - 4x + 8 &= x^2 + 4x + 4\ x &= frac{1}{2}end{align*}$

Hence $CE = FC + x = frac{5}{2} Rightarrowboxed{mathrm{(D)} frac{5}{2}}$ .

Solution 2

Call the point of tangency point $F$ and the midpoint of $AB$ as $G$ . $CF=2$ by Tangent Theorem. Notice that $angle EGF=frac{180-2cdotangle CGF}{2}=90-angle CGF$ . Thus, $angle EGF=angle FCG$ and $tanEGF=tanFCG=frac{1}{2}$ . Solving $EF=frac{1}{2}$ . Adding, the answer is $frac{5}{2}$ .

Solution 3

Clearly, $EA = EF = BG$ . Thus, the sides of right triangle $CDE$ are in arithmetic progression. Thus it is similar to the triangle $3 - 4 - 5$ and since $DC = 2$ , $CE = 5/2$ .

Solution 4

$[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2, G=(1,0); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); label("$G$",G,(0,-1)); dot(G); draw(G--C); label("$sqrt{5}$",(G+C)/2,(-1,0)); [/asy]$

Let us call the midpoint of side $AB$ , point $G$ . Since the semicircle has radius 1, we can do the Pythagorean theorem on sides $GB, BC, GC$ . We get $GC=sqrt{5}$ . We then know that $CF=2$ by Pythagorean theorem. Then by connecting $EG$ , we get similar triangles $EFG$ and $GFC$ . Solving the ratios, we get $x=frac{1}{2}$ , so the answer is $frac{5}{2} Rightarrowboxed{mathrm{(D)} frac{5}{2}}$ .

Solution 5

Using the diagram as drawn in Solution 5, let the total area of square $ABCD$ be divided into the triangles $DCE$ , $EAG$ , $CGB$ , and $EGC$ . Let x be the length of AE. Thus, the area of each triangle can be determined as follows:

$[DCE = frac{DCcdot{DE}}{2} = frac{2cdot(2-x)}{2} = 1-x]$

$[EAG= frac{AEcdot{AG}}{2} = frac{1cdot{x}}{2} = frac{x}{2}]$

$[CGB = frac{GBcdot{CB}}{2} = frac{1cdot(2)}{2} = 1]$

$[EGC= frac{EGcdot{GC}}{2} = frac{sqrt{4+(2-x)^2}}{2}]$ (the length of CE is calculated with the Pythagorean Theorem, lines GE and CE are perpendicular by definition of tangent)

Adding up the areas and equating to the area of the total square (2*2=4), we get

$[1-x+frac{x}{2}+1+ frac{sqrt{4+(2-x)^2}}{2} = 4]$

Solving for x:

$[2-2x+x+1+sqrt{x^2-4x+8}=8]$ $[sqrt{x^2-4x+8}=x+2]$ $[x^2-4x+8=x^2+4x+4]$ $[8-4x=4x+4 rightarrow x=frac{1}{2}]$

Solving for length of CE with the value we have for x: $[sqrt{4+(2-x)^2} = sqrt{4+(3/2)^2} = sqrt{25/4} = boxed{frac{5}{2}}]$
Solution 1

$[asy] import graph; size(400); defaultpen(fontsize(10)); pair OA=(-1,0),OB=(2/3,8/9),OC=(2/3,-8/9),OD=(0,0),E=(2/3,0); real t = 2.5; pair OA1=(-2+2*t,0),OB1=(4/3+2*t,16/9),OC1=(4/3+2*t,-16/9),OD1=(0+2*t,0),E1=(4/3+2*t,0); draw(Circle(OD,2)); draw(Circle(OA,1)); draw(Circle(OB,8/9)); draw(Circle(OC,8/9)); draw(OA--OB--OC--cycle); draw(OD--OB--OB+(OB-OD)*4/5); draw(OA--E); label("$O_{A}$",OA,(-1,0)); label("$O_{B}$",OB,(-1,1)); label("$O_{C}$",OC,(-1,-1)); label("$O_{D}$",OD,(-1,-1)); label("$E$",E,(0.5,-1)); label("$r$",OB+(OB-OD)*2/5,(-0.5,1)); label("$r$",(1*OA+3*OB)/4,(-0.5,1)); dot(OA^^OB^^OC^^OD^^E); draw(OA1--OB1--OC1--cycle); draw(OD1--OB1); draw(OA1--E1); label("$O_{A}$",OA1,(-1,0)); label("$O_{B}$",OB1,(1,1)); label("$O_{C}$",OC1,(1,-1)); label("$O_{D}$",OD1,(0,-1)); label("$E$",E1,(1,0)); label("$1+r$",(OA1+OB1)/2,(-0.5,1)); label("$r$",(E1+OB1)/2,(1,0)); label("$r$",(E1+OC1)/2,(1,0)); label("$2-r$",(OB1+OD1)/2,(-1,0)); label("$1$",(OA1+OD1)/2,(0,-1)); label("$x$",(E1+OD1)/2,(0,-1)); dot(OA1^^OB1^^OC1^^OD1^^E1); [/asy]$

Let $O_{i}$ be the center of circle $i$ for all $i in {A,B,C,D}$ and let $E$ be the tangent point of $B,C$ . Since the radius of $D$ is the diameter of $A$ , the radius of $D$ is $2$ . Let the radius of $B,C$ be $r$ and let $O_{D}E = x$ . If we connect $O_{A},O_{B},O_{C}$ , we get an isosceles triangle with lengths $1 + r, 2r$ . Then right triangle $O_{D}O_{B}O_{E}$ has legs $r, x$ and hypotenuse $2-r$ . Solving for $x$ , we get $x^2 = (2-r)^2 - r^2 Longrightarrow x = sqrt{4-4r}$ .

Also, right triangle $O_{A}O_{B}O_{E}$ has legs $r, 1+x$ , and hypotenuse $1+r$ . Solving,

$begin{eqnarray*} r^2 + (1+sqrt{4-4r})^2 &=& (1+r)^2\ 1+4-4r+2sqrt{4-4r}&=& 2r + 1\ 1-r &=& left(frac{6r-4}{4}right)^2\ frac{9}{4}r^2-2r&=& 0\ r &=& frac 89 end{eqnarray*}$

So the answer is $boxed{mathrm{(D)} frac{8}{9}}$ .

Solution 2

$[asy] unitsize(15mm); pair A=(0,1),B=(-8/9,-2/3),C=(8/9,-2/3),D=(0,0), E=(0,-2/3); draw(Circle(D,2)); draw(Circle(A,1)); draw(Circle(B,8/9)); draw(Circle(C,8/9)); draw(A--B--C--A); draw(B--D--C); draw(A--E); dot(A);dot(B);dot(C);dot(D);dot(E); label("(D)", D,NW); label("(A)", A,N); label("(B)", B,W); label("(C)", C,E); label("(E)", E,SE); label("(1)",(-.4,.7)); label("(1)",(0,0.5),W); label("(r)", (-.8,-.1)); label("(r)", (-4/9,-2/3),S); label("(h)", (0,-1/3), W); [/asy]$ Note that $BD= 2-r$ since $D$ is the center of the larger circle of radius $2$ . Using the Pythagorean Theorem on $triangle BDE$ ,

$begin{align*} r^2 + h^2 &= (2-r)^2 \ r^2 + h^2 &= 4 - 4r + r^2 \ h^2 &= 4 - 4r \ h &= 2sqrt{1-r} end{align*}$

Now using the Pythagorean Theorem on $triangle BAE$ ,

$begin{align*} r^2 + (h+1)^2 &= (r+1)^2 \ r^2 + h^2 + 2h + 1 &= r^2 + 2r + 1 \ h^2 + 2h &= 2r end{align*}$

Substituting $h$ ,

$begin{align*} (4-4r) + 4sqrt{1-r} &= 2r \ 4sqrt{1-r} &= 6r - 4 \ 16-16r &= 36r^2 - 48r + 16 \ 0 &= 36r^2 - 32r \ r &= frac{32}{36} = frac{8}{9} Longrightarrow qquad textbf{(D)} end{align*}$

Solution 3

We can apply Descartes' Circle Formula.

The four circles have curvatures $-frac{1}{2}, 1, frac{1}{r}$ , and $frac{1}{r}$ .

We have $2((-frac{1}{2})^2+1^2+frac {1}{r^2}+frac{1}{r^2})=(-frac{1}{2}+1+frac{1}{r}+frac{1}{r})^2$

Simplifying, we get $frac{10}{4}+frac{4}{r^2}=frac{1}{4}+frac{2}{r}+frac{4}{r^2}$

$frac{2}{r}=frac{9}{4}$

$r=frac{8}{9} Longrightarrow qquad textbf{(D)}$
Solution 1

Casework:
1. $0 + 0 = 0$ . The probability that $a < frac{1}{2}$ and $b < frac{1}{2}$ is $left(frac 12right)^2 = frac{1}{4}$ . Notice that the sum $a+b$ ranges from $0$ to $1$ with a symmetric distribution across $a+b=c=frac 12$ , and we want $c < frac 12$ . Thus the chance is $frac{frac{1}{4}}2 = frac 18$ .
2. $0 + 1 = 1$ . The probability that $a < frac 12$ and $b > frac 12$ is $frac 14$ , but now $frac{1}{2} < a+b = c < frac 32$ , which makes $C = 1$ automatically. Hence the chance is $frac 14$ .
3. $1 + 0 = 1$ . This is the same as the previous case.
4. $1 + 1 = 2$ . We recognize that this is equivalent to the first case.
Our answer is $2left(frac 18 + frac 14 right) = frac 34 Rightarrow mathrm{(E)}$ .

Solution 2

Use areas to deal with this continuous probability problem. Set up a unit square with values of $a$ on x-axis and $b$ on y-axis.

If $a + b < 1/2$ then this will work because $A = B = C = 0$ . Similarly if $a + b > 3/2$ then this will work because in order for this to happen, $a$ and $b$ are each greater than $1/2$ making $A = B = 1$ , and $C = 2$ . Each of these triangles in the unit square has area of 1/8.

The only case left is when $C = 1$ . Then each of $A$ and $B$ must be 1 and 0, in any order. These cut off squares of area 1/2 from the upper left and lower right corners of the unit square.

Then the area producing the desired result is 3/4. Since the area of the unit square is 1, the probability is $frac 34$ .
Solution 1

This is an infinite geometric series, which sums to $frac{cos^0 theta}{1 - cos^2 theta} = 5 Longrightarrow 1 = 5 - 5cos^2 theta Longrightarrow cos^2 theta = frac{4}{5}$ . Using the formula $cos 2theta = 2cos^2 theta - 1 = 2left(frac 45right) - 1 = frac 35 Rightarrow mathrm{(D)}$ .

Solution 2

$[sum_{n = 0}^{infty}{cos^{2n}}theta = cos^{0}theta + cos^{2}theta + cos^{4}theta + ... = 5]$

Multiply both sides by $cos^{2}theta$ to get:

$[cos^{2}theta + cos^{4}theta + cos^{6}theta + ... = 5*cos^{2}theta]$

Subtracting the two equations, we get:

$[cos^{0}theta=5-5*cos^{2}theta]$

Simplifying, we get $cos^{2}theta=frac{4}{5}$ . Using the formula $cos 2theta = 2cos^2 theta - 1 = 2left(frac 45right) - 1 = frac 35 Rightarrow mathrm{(D)}$ .
Solution 1

We draw the three spheres of radius $1$ :

And then add the sphere of radius $2$ :

The height from the center of the bottom sphere to the plane is $1$ , and from the center of the top sphere to the tip is $2$ .

We now need the vertical height of the centers. If we connect the centers, we get a triangular pyramid with an equilateral triangle base. The distance from the vertex of the equilateral triangle to its centroid can be found by $30-60-90 triangle$ s to be $frac{2sqrt{3}}{3}$ .

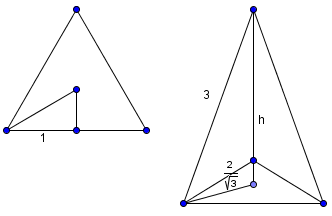
By the Pythagorean Theorem, we have $left(frac{2}{sqrt{3}}right)^2 + h^2 = 3^2 Longrightarrow h = frac{sqrt{69}}{3}$ . Adding the heights up, we get $frac{sqrt{69}}{3} + 1 + 2 Rightarrowboxed{mathrm{(B)} 3+frac{sqrt{69}}{3}}$

Solution 2

Connect the centers of the spheres. Note that the resulting prism is a tetrahedron with base lengths of 2 and side lengths of 3. Drop a height from the top of the tetrahedron to the centroid of its equilateral triangle base. Using the Pythagorean Theorem, it is easy to see that the circumradius of the base is $dfrac { 2 sqrt {3 } } {3}$ . We can use PT again to find the height of the tetrahedron given its base's circumradius and it's leg lengths. Finally, we add the distance from the top of the tetrahedron to the top of the sphere of radius 2 and the distance from the bottom of the prism to the ground to get an answer of $3 + dfrac{sqrt{69}}{3}$ .
We have to evaluate the answer choices and use process of elimination:
- $mathrm{(A)}$ : We are given that $a_1 = b_1 = 0$ , so $z_1 = 0$ . If one of the roots is zero, then $P(0) = c_0 = 0$ .
- $mathrm{(B)}$ : By Vieta's formulas, we know that $-frac{c_{2003}}{c_{2004}}$ is the sum of all of the roots of $P(x)$ . Since that is real, $sum_{k = 1}^{2004}{b_k}=0=sum_{k = 1}^{2004}{a_k}$ , and $frac{c_{2003}}{c_{2004}}=0$ , so $c_{2003}=0$ .
- $mathrm{(C)}$ : All of the coefficients are real. For sake of contradiction suppose none of $b_{2ldots 2004}$ are zero. Then for each complex root $z_i$ , its complex conjugate $overline{z_i} = a_i - b_ik$ is also a root. So the roots should pair up, but we have an odd number of imaginary roots! (Remember that $b_1 = 0$ .) This gives us the contradiction, and therefore the product is equal to zero.
- $mathrm{(D)}$ : We are given that $sum_{k = 1}^{2004}{a_k} = sum_{k = 1}^{2004}{b_k}$ . Since the coefficients are real, it follows that if a root is complex, its conjugate is also a root; and the sum of the imaginary parts of complex conjugates is zero. Hence the RHS is zero.
There is, however, no reason to believe that $boxed{mathrm{E}}$ should be zero (in fact, that quantity is $P(1)$ , and there is no evidence that $1$ is a root of $P(x)$ ).
$[asy] pair A=(-.5,0), B=(.5,0), C=(0,3**(.5)/2), D=(0,-3**(.5)/2); draw(arc(A,2,-60,60),blue); draw(arc(B,2,120,240),blue); draw(circle(C,1),red); draw(A--(.5,3^.5)); draw(B--(-.5,3^.5)); draw(A--(.5,-3^.5)); draw(B--(-.5,-3^.5)); draw(A--B); dot(A);dot(B);dot(C);dot(D); label("(1)",(0,0),N); label("(1)",A/2+D/2,W); label("(1)",A/2+C/2,W); label("(1)",B/2+D/2,E); label("(1)",B/2+C/2,E); label("(1)",A/2+3D/2,W); label("(1)",A/2+3C/2,W); label("(1)",B/2+3D/2,E); label("(1)",B/2+3C/2,E); label("(A)",A,W); label("(B)",B,E); label("(C)",C,W); label("(D)",D,E); [/asy]$ As the red circles move about segment $AB$ , they cover the area we are looking for. On the left side, the circle must move around pivoted on $B$ . On the right side, the circle must move pivoted on $A$ However, at the top and bottom, the circle must lie on both A and B, giving us our upper and lower bounds.This egg-like shape is $S$ . $[asy] pair A=(-.5,0), B=(.5,0), C=(0,3**(.5)/2), D=(0,-3**(.5)/2); draw(arc(A,2,-60,60),blue); draw(arc(B,2,120,240),blue); draw(arc(C,1,60,120),red); draw(arc(D,1,-120,-60),red); draw(A--(.5,3^.5)); draw(B--(-.5,3^.5)); draw(A--(.5,-3^.5)); draw(B--(-.5,-3^.5)); draw(A--B); dot(A);dot(B);dot(C);dot(D); label("(A)",A,W); label("(B)",B,E); label("(C)",C,W); label("(D)",D,E); label("(1)",(0,0),N); label("(1)",A/2+D/2,W); label("(1)",A/2+C/2,W); label("(1)",B/2+D/2,E); label("(1)",B/2+C/2,E); label("(1)",A/2+3D/2,W); label("(1)",A/2+3C/2,W); label("(1)",B/2+3D/2,E); label("(1)",B/2+3C/2,E); [/asy]$ The area of the region can be found by dividing it into several sectors, namely $begin{align*} A &= 2(mathrm{Blue Sector}) + 2(mathrm{Red Sector}) - 2(mathrm{Equilateral Triangle}) \ A &= 2left(frac{120^circ}{360^circ} cdot pi (2)^2right) + 2left(frac{60^circ}{360^circ} cdot pi (1)^2right) - 2left(frac{(1)^2sqrt{3}}{4}right) \ A &= frac{8pi}{3} + frac{pi}{3} - frac{sqrt{3}}{2} \ A &= 3pi - frac{sqrt{3}}{2} Longrightarrow textbf {(C)}end{align*}$
This is an infinite geometric series with common ratio $frac{1}{x^3}$ and initial term $x^{-1} + 3x^{-2} + 3x^{-3}$ , so $a_x = left(frac{1}{x} + frac{3}{x^2} + frac{3}{x^3}right)left(frac{1}{1-frac{1}{x^3}}right)$ $= frac{x^2 + 3x + 3}{x^3} cdot frac{x^3}{x^3 - 1}$ $= frac{x^2 + 3x + 3}{x^3 - 1}$ $= frac{(x+1)^3 - 1}{x(x^3 - 1)}$ .

Alternatively, we could have used the algebraic manipulation for repeating decimals,

$begin{align*} a_x &= frac{1}{x}+frac{3}{x^2}+frac{3}{x^3}+frac{1}{x^4}+frac{3}{x^5}+frac{3}{x^6}+cdots \ a_x cdot x^3 &= x^2+3x+3+a_x\ a_x(x^3-1) &= x^2+3x+3\ a_x &= frac{x^2+3x+3}{x^3-1}=frac{(x+1)^3-1}{x(x^3-1)} end{align*}$

Telescoping,

$begin{align*} a_4a_5cdots a_{99}&= frac{(5^3-1)(6^3-1)cdots (100^3-1)}{4 cdot 5 cdot 6 cdot cdots cdot 99 cdot (4^3-1)(5^3-1)cdots(99^3-1)}\ a_4a_5cdots a_{99}&= frac{999999}{4 cdot 5 cdot 6 cdot cdots cdot 99 cdot 63}=frac{13 cdot 37 cdot 33 cdot 6}{99!}end{align*}$

Some factors cancel, (after all, $13 cdot 37 cdot 33 cdot 6$ isn't one of the answer choices)

$[frac{13 cdot 37 cdot 33 cdot 6}{99!}=frac{13 cdot 37 cdot 2}{98!}]$

Since the only factor in the numerator that goes into $98$ is $2$ , $n$ is minimized. Therefore the answer is $13 cdot 37 cdot 2=962 Rightarrow text {(E)}$ .

以上解析方式仅供参考

学术活动报名扫码了解！免费领取历年真题！

Previous post: 2004AMC10B真题与答案解析 Next post: 2003AMC10A真题与答案解析

2004 AMC12A 真题及答案详细解析

2004 AMC 12A 真题

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Problem 8

Problem 9

Problem 10

Problem 11

Problem 12

Problem 13

Problem 14

Problem 15

Problem 16

Problem 17

Problem 18

Problem 19

Problem 20

Problem 21

Problem 22

Problem 23

Problem 24

Problem 25

2004 AMC12 A 真题答案详细解析

Solution 1

Solution 2

Solution

Solution 2

Solution 1

Solution 2

Solution 3

Solution 1

Solution 2

Solution 1

Solution 2

Solution 3

Solution 1

Solution 2

Solution 3

Solution 1

Solution 2

Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 1

Solution 2

Solution 3

Solution 1

Solution 2

Solution 1

Solution 2

Solution 1

Solution 2

国际竞赛真题资料-点击免费领取！

美高学分项目重磅来袭！立即了解

2025欧几里得数学竞赛报名开启！

在线登记

最新发布

热门标签