Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2002 AMC12A 真题及答案详细解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月5日上午10:03

2002 AMC 12A 真题

答案详细解析请参考文末

Problem 1

Compute the sum of all the roots of $(2x+3)(x-4)+(2x+3)(x-6)=0$

$mathrm{(A) } frac{7}{2}qquad mathrm{(B) } 4qquad mathrm{(C) } 5qquad mathrm{(D) } 7qquad mathrm{(E) } 13$

Problem 2

Cindy was asked by her teacher to subtract 3 from a certain number and then divide the result by 9. Instead, she subtracted 9 and then divided the result by 3, giving an answer of 43. What would her answer have been had she worked the problem correctly?

$mathrm{(A) } 15qquad mathrm{(B) } 34qquad mathrm{(C) } 43qquad mathrm{(D) } 51qquad mathrm{(E) } 138$

Problem 3

According to the standard convention for exponentiation, $[2^{2^{2^{2}}} = 2^{left(2^{left(2^2right)}right)} = 2^{16} = 65536.]$

If the order in which the exponentiations are performed is changed, how many other values are possible?

$mathrm{(A) } 0qquad mathrm{(B) } 1qquad mathrm{(C) } 2qquad mathrm{(D) } 3qquad mathrm{(E) } 4$

Problem 4

Find the degree measure of an angle whose complement is 25% of its supplement.

$mathrm{(A) 48 } qquad mathrm{(B) 60 } qquad mathrm{(C) 75 } qquad mathrm{(D) 120 } qquad mathrm{(E) 150 }$

Problem 5

Each of the small circles in the figure has radius one. The innermost circle is tangent to the six circles that surround it, and each of those circles is tangent to the large circle and to its small-circle neighbors. Find the area of the shaded region.

$[asy] import graph; unitsize(.3cm); path c=Circle((0,2),1); filldraw(Circle((0,0),3),grey,black); filldraw(Circle((0,0),1),white,black); filldraw(c,white,black); filldraw(rotate(60)*c,white,black); filldraw(rotate(120)*c,white,black); filldraw(rotate(180)*c,white,black); filldraw(rotate(240)*c,white,black); filldraw(rotate(300)*c,white,black); [/asy]$

$text{(A)} pi qquad text{(B)} 1.5pi qquad text{(C)} 2pi qquad text{(D)} 3pi qquad text{(E)} 3.5pi$

Problem 6

For how many positive integers $m$ does there exist at least one positive integer $n$ such that $m cdot n le m + n$ ?

$mathrm{(A) } 4qquad mathrm{(B) } 6qquad mathrm{(C) } 9qquad mathrm{(D) } 12qquad mathrm{(E) }$ infinitely many

Problem 7

A $45^circ$ arc of circle A is equal in length to a $30^circ$ arc of circle B. What is the ratio of circle A's area and circle B's area?

$text{(A)} 4/9 qquad text{(B)} 2/3 qquad text{(C)} 5/6 qquad text{(D)} 3/2 qquad text{(E)} 9/4$

Problem 8

Betsy designed a flag using blue triangles, small white squares, and a red center square, as shown. Let $B$ be the total area of the blue triangles, $W$ the total area of the white squares, and $R$ the area of the red square. Which of the following is correct?

$[asy] unitsize(3mm); fill((-4,-4)--(-4,4)--(4,4)--(4,-4)--cycle,blue); fill((-2,-2)--(-2,2)--(2,2)--(2,-2)--cycle,red); path onewhite=(-3,3)--(-2,4)--(-1,3)--(-2,2)--(-3,3)--(-1,3)--(0,4)--(1,3)--(0,2)--(-1,3)--(1,3)--(2,4)--(3,3)--(2,2)--(1,3)--cycle; path divider=(-2,2)--(-3,3)--cycle; fill(onewhite,white); fill(rotate(90)*onewhite,white); fill(rotate(180)*onewhite,white); fill(rotate(270)*onewhite,white); [/asy]$

$text{(A)} B = W qquad text{(B)} W = R qquad text{(C)} B = R qquad text{(D)} 3B = 2R qquad text{(E)} 2R = W$

Problem 9

Jamal wants to save 30 files onto disks, each with 1.44 MB space. 3 of the files take up 0.8 MB, 12 of the files take up 0.7 MB, and the rest take up 0.4 MB. It is not possible to split a file onto 2 different disks. What is the smallest number of disks needed to store all 30 files?

$text{(A)} 12 qquad text{(B)} 13 qquad text{(C)} 14 qquad text{(D)} 15 qquad text{(E)} 16$

Problem 10

Sarah places four ounces of coffee into an eight-ounce cup and four ounces of cream into a second cup of the same size. She then pours half the coffee from the first cup to the second and, after stirring thoroughly, pours half the liquid in the second cup back to the first. What fraction of the liquid in the first cup is now cream?

$mathrm{(A) } frac{1}{4}qquad mathrm{(B) } frac13qquad mathrm{(C) } frac38qquad mathrm{(D) } frac25qquad mathrm{(E) } frac12$

Problem 11

Mr. Earl E. Bird gets up every day at 8:00 AM to go to work. If he drives at an average speed of 40 miles per hour, he will be late by 3 minutes. If he drives at an average speed of 60 miles per hour, he will be early by 3 minutes. How many miles per hour does Mr. Bird need to drive to get to work exactly on time?

$text{(A)} 45 qquad text{(B)} 48 qquad text{(C)} 50 qquad text{(D)} 55 qquad text{(E)} 58$

Problem 12

Both roots of the quadratic equation $x^2 - 63x + k = 0$ are prime numbers. The number of possible values of $k$ is

$text{(A)} 0 qquad text{(B)} 1 qquad text{(C)} 2 qquad text{(D)} 4 qquad text{(E) more than 4}$

Problem 13

Two different positive numbers $a$ and $b$ each differ from their reciprocals by $1$ . What is $a+b$ ?

$text{(A) }1 qquad text{(B) }2 qquad text{(C) }sqrt 5 qquad text{(D) }sqrt 6 qquad text{(E) }3$

Problem 14

For all positive integers $n$ , let $f(n)=log_{2002} n^2$ . Let $N=f(11)+f(13)+f(14)$ . Which of the following relations is true?

$text{(A) }N<1 qquad text{(B) }N=1 qquad text{(C) }1<N<2 qquad text{(D) }N=2 qquad text{(E) }N>2$

Problem 15

The mean, median, unique mode, and range of a collection of eight integers are all equal to 8. The largest integer that can be an element of this collection is

$text{(A) }11 qquad text{(B) }12 qquad text{(C) }13 qquad text{(D) }14 qquad text{(E) }15$

Problem 16

Tina randomly selects two distinct numbers from the set ${1, 2, 3, 4, 5}$ , and Sergio randomly selects a number from the set ${1, 2, ldots, 10}$ . What is the probability that Sergio's number is larger than the sum of the two numbers chosen by Tina?

$text{(A)} 2/5 qquad text{(B)} 9/20 qquad text{(C)} 1/2 qquad text{(D)} 11/20 qquad text{(E)} 24/25$

Problem 17

Several sets of prime numbers, such as ${7,83,421,659}$ use each of the nine nonzero digits exactly once. What is the smallest possible sum such a set of primes could have?

$text{(A) }193 qquad text{(B) }207 qquad text{(C) }225 qquad text{(D) }252 qquad text{(E) }447$

Problem 18

Let $C_1$ and $C_2$ be circles defined by $(x-10)^2 + y^2 = 36$ and $(x+15)^2 + y^2 = 81$ respectively. What is the length of the shortest line segment $PQ$ that is tangent to $C_1$ at $P$ and to $C_2$ at $Q$ ?

$text{(A) }15 qquad text{(B) }18 qquad text{(C) }20 qquad text{(D) }21 qquad text{(E) }24$

Problem 19

The graph of the function $f$ is shown below. How many solutions does the equation $f(f(x))=6$ have?

$[asy] import graph; size(200); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=4; pair P1=(-7,-4), P2=(-2,6), P3=(0,0), P4=(1,6), P5=(5,-6); real[] xticks={-7,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; real[] yticks={-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; draw(P1--P2--P3--P4--P5); dot("(-7, -4)",P1); dot("(-2, 6)",P2,LeftSide); dot("(1, 6)",P4); dot("(5, -6)",P5); xaxis("$x$",-7.5,7,Ticks(xticks),EndArrow(6)); yaxis("$y$",-6.5,7,Ticks(yticks),EndArrow(6)); [/asy]$

$text{(A) }2 qquad text{(B) }4 qquad text{(C) }5 qquad text{(D) }6 qquad text{(E) }7$

Problem 20

Suppose that $a$ and $b$ are digits, not both nine and not both zero, and the repeating decimal $0.overline{ab}$ is expressed as a fraction in lowest terms. How many different denominators are possible?

$text{(A) }3 qquad text{(B) }4 qquad text{(C) }5 qquad text{(D) }8 qquad text{(E) }9$

Problem 21

Consider the sequence of numbers: $4,7,1,8,9,7,6,dots$ For $n>2$ , the $n$ -th term of the sequence is the units digit of the sum of the two previous terms. Let $S_n$ denote the sum of the first $n$ terms of this sequence. The smallest value of $n$ for which $S_n>10,000$ is:

$text{(A) }1992 qquad text{(B) }1999 qquad text{(C) }2001 qquad text{(D) }2002 qquad text{(E) }2004$

Problem 22

Triangle $ABC$ is a right triangle with $angle ACB$ as its right angle, $mangle ABC = 60^{circ}$ , and $AB = 10$ . Let $P$ be randomly chosen inside $triangle ABC$ , and extend $overline{BP}$ to meet $overline{AC}$ at $D$ . What is the probability that $BD > 5sqrt{2}$ ?

$textbf{(A)} frac{2-sqrt2}{2}qquadtextbf{(B)} frac{1}{3}qquadtextbf{(C)} frac{3-sqrt3}{3}qquadtextbf{(D)} frac{1}{2}qquadtextbf{(E)} frac{5-sqrt5}{5}$

Problem 23

In triangle $ABC$ , side $AC$ and the perpendicular bisector of $BC$ meet in point $D$ , and $BD$ bisects $angle ABC$ . If $AD = 9$ and $DC = 7$ , what is the area of triangle $ABD$ ?

$text{(A)} 14 qquad text{(B)} 21 qquad text{(C)} 28 qquad text{(D)} 14sqrt5 qquad text{(E)} 28sqrt5$

Problem 24

Find the number of ordered pairs of real numbers $(a,b)$ such that $(a+bi)^{2002} = a-bi$ .

$text{(A) }1001 qquad text{(B) }1002 qquad text{(C) }2001 qquad text{(D) }2002 qquad text{(E) }2004$

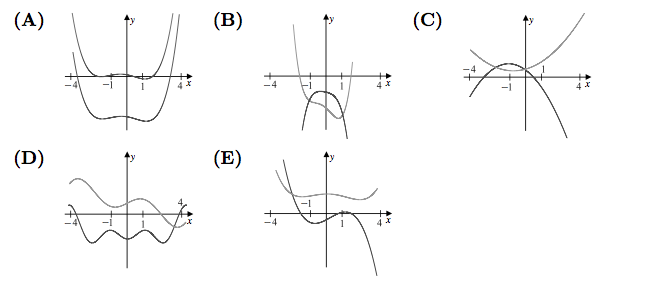
Problem 25

The nonzero coefficients of a polynomial $P$ with real coefficients are all replaced by their mean to form a polynomial $Q$ . Which of the following could be a graph of $y = P(x)$ and $y = Q(x)$ over the interval $-4leq x leq 4$ ?

2002 AMC12A 真题答案详细解析

Solution 1
We expand to get $2x^2-8x+3x-12+2x^2-12x+3x-18=0$ which is $4x^2-14x-30=0$ after combining like terms. Using the quadratic part of Vieta's Formulas, we find the sum of the roots is $frac{14}4 = boxed{text{(A)} 7/2}$ .
Solution 2
Combine terms to get $(2x+3)cdotBig( (x-4)+(x-6) Big) = (2x+3)(2x-10)=0$ , hence the roots are $-frac{3}{2}$ and $5$ , thus our answer is $-frac{3}{2}+5=boxed{text{(A)} 7/2}$ .
We work backwards; the number that Cindy started with is $3(43)+9=138$ . Now, the correct result is $frac{138-3}{9}=frac{135}{9}=15$ . Our answer is $boxed{text{(A)} 15}$ .
The best way to solve this problem is by simple brute force.It is convenient to drop the usual way how exponentiation is denoted, and to write the formula as , where denotes exponentiation. We are now examining all ways to add parentheses to this expression. There are 5 ways to do so:
1. $2uparrow (2uparrow (2uparrow 2))$
2. $2uparrow ((2uparrow 2)uparrow 2)$
3. $((2uparrow 2)uparrow 2)uparrow 2$
4. $(2uparrow (2uparrow 2))uparrow 2$
5. $(2uparrow 2)uparrow (2uparrow 2)$
We can note that $2uparrow (2uparrow 2) = (2uparrow 2)uparrow 2 =16$ . Therefore options 1 and 2 are equal, and options 3 and 4 are equal. Option 1 is the one given in the problem statement. Thus we only need to evaluate options 3 and 5.

$((2uparrow 2)uparrow 2)uparrow 2 = 16uparrow 2 = 256$

$(2uparrow 2)uparrow (2uparrow 2) = 4 uparrow 4 = 256$

Thus the only other result is $256$ , and our answer is $boxed{text{(B)} 1}$ .
Solution 1

We can create an equation for the question, $4(90-x)=(180-x)$

$360-4x=180-x$

$3x=180$

After simplifying, we get $x=60 Rightarrow mathrm {(B)}$

Solution 2

Given that the complementary angle is $frac{1}{4}$ of the supplementary angle. Subtracting the complementary angle from the supplementary angle, we have $90^{circ}$ as $frac{3}{4}$ of the supplementary angle.

Thus the degree measure of the supplementary angle is $120^{circ}$ , and the degree measure of the desired angle is $180^{circ} - 120^{circ} = 60^{circ}$ . $mathrm {(B)}$
The outer circle has radius $1+1+1=3$ , and thus area $9pi$ . The little circles have area $pi$ each; since there are 7, their total area is $7pi$ . Thus, our answer is $9pi-7pi=boxed{2piRightarrow text{(C)}}$ .
Solution 1

For any $m$ we can pick $n=1$ , we get $m cdot 1 le m + 1$ , therefore the answer is $boxed{text{(E) infinitely many}}$ .

Solution 2

Another solution, slightly similar to this first one would be using Simon's Favorite Factoring Trick.

$(m-1)(n-1) leq 1$

Let $n=1$ , then

$0 leq 1$

This means that there are infinitely many numbers $m$ that can satisfy the inequality. So the answer is $boxed{text{(E) infinitely many}}$ .

Solution 3

If we subtract $n$ from both sides of the equation, we get $m cdot n - n le m$ . Factor the left side to get $(m - 1)(n) le m$ . Divide both sides by $(m-1)$ and we get $n le frac {m}{m-1}$ . The fraction $frac {m}{m-1} > 1$ if $m > 1$ . There is an infinite amount of integers greater than 1, therefore the answer is $boxed{text{(E) infinitely many}}$ .
Solution 1

Let $r_1$ and $r_2$ be the radii of circles $A$ and $B$ , respectively.

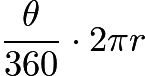It is well known that in a circle with radius $r$ , a subtended arc opposite an angle of $theta$ degrees has length $frac{theta}{360} cdot 2pi r$ .

Using that here, the arc of circle A has length $frac{45}{360}cdot2pi{r_1}=frac{r_1pi}{4}$ . The arc of circle B has length $frac{30}{360} cdot 2pi{r_2}=frac{r_2pi}{6}$ . We know that they are equal, so $frac{r_1pi}{4}=frac{r_2pi}{6}$ , so we multiply through and simplify to get $frac{r_1}{r_2}=frac{2}{3}$ . As all circles are similar to one another, the ratio of the areas is just the square of the ratios of the radii, so our answer is $boxed{text{(A)} 4/9}$ .

Solution 2

The arc of circle $A$ is $frac{45}{30}=frac{3}{2}$ that of circle $B$ .

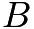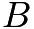The circumference of circle $A$ is $frac{2}{3}$ that of circle $B$ ( $B$ is the larger circle).

The radius of circle $A$ is $frac{2}{3}$ that of circle $B$ .

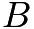The area of circle $A$ is ${left(frac{2}{3}right)}^2=boxed{text{(A)} 4/9}$ that of circle $B$ .
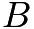The blue that's touching the center red square makes up 8 triangles, or 4 squares. Each of the corners is 2 squares and each of the edges is 1, totaling 12 squares. There are 12 white squares, thus we have $boxed{B=WRightarrow text{(A)}}$ .
A 0.8 MB file can either be on its own disk, or share it with a 0.4 MB. Clearly it is better to pick the second possibility. Thus we will have 3 disks, each with one 0.8 MB file and one 0.4 MB file.We are left with 12 files of 0.7 MB each, and 12 files of 0.4 MB each. Their total size is $12cdot (0.7 + 0.4) = 13.2$ MB. The total capacity of 9 disks is $9cdot 1.44 = 12.96$ MB, hence we need at least 10 more disks. And we can easily verify that 10 disks are indeed enough: six of them will carry two 0.7 MB files each, and four will carry three 0.4 MB files each.Thus our answer is $3+10 = boxed{ text{(B)} 13 }$ .
We will simulate the process in steps.In the beginning, we have:
- $4$ ounces of coffee in cup $1$
- $4$ ounces of cream in cup $2$
In the first step we pour $4/2=2$ ounces of coffee from cup $1$ to cup $2$ , getting:
- $2$ ounces of coffee in cup $1$
- $2$ ounces of coffee and $4$ ounces of cream in cup $2$
In the second step we pour $2/2=1$ ounce of coffee and $4/2=2$ ounces of cream from cup $2$ to cup $1$ , getting:
- $2+1=3$ ounces of coffee and $0+2=2$ ounces of cream in cup $1$
- the rest in cup $2$
Hence at the end we have $3+2=5$ ounces of liquid in cup $1$ , and out of these $2$ ounces is cream. Thus the answer is $boxed{text{(D) } frac 25}$ .
Solution 1Let the time he needs to get there in be t and the distance he travels be d. From the given equations, we know that $d=left(t+frac{1}{20}right)40$ and $d=left(t-frac{1}{20}right)60$ . Setting the two equal, we have $40t+2=60t-3$ and we find $t=frac{1}{4}$ of an hour. Substituting t back in, we find $d=12$ . From $d=rt$ , we find that r, and our answer, is $boxed{text{(B)} 48 }$ .

Solution 2

Since either time he arrives at is 3 minutes from the desired time, the answer is merely the harmonic mean of 40 and 60. The harmonic mean of a and b is $2002 AMC12A 真题及答案详细解析$ . In this case, a and b are 40 and 60, so our answer is $frac{4800}{100}=48$ , so $boxed{text{(B)} 48}$ .

Solution 3

A more general form of the argument in Solution 2, with proof:

Let $d$ be the distance to work, and let $s$ be the correct average speed. Then the time needed to get to work is $t=frac ds$ .

We know that $t+frac 3{60} = frac d{40}$ and $t-frac 3{60} = frac d{60}$ . Summing these two equations, we get: $2t = frac d{40} + frac d{60}$ .

Substituting $t=frac ds$ and dividing both sides by $d$ , we get $frac 2s = frac 1{40} + frac 1{60}$ , hence $s=boxed{48}$ .

(Note that this approach would work even if the time by which he is late was different from the time by which he is early in the other case - we would simply take a weighted sum in step two, and hence obtain a weighted harmonic mean in step three.)
Consider a general quadratic with the coefficient of $x^2$ being $1$ and the roots being $r$ and $s$ . It can be factored as $(x-r)(x-s)$ which is just $x^2-(r+s)x+rs$ . Thus, the sum of the roots is the negative of the coefficient of $x$ and the product is the constant term. (In general, this leads to Vieta's Formulas).We now have that the sum of the two roots is $63$ while the product is $k$ . Since both roots are primes, one must be $2$ , otherwise the sum would be even. That means the other root is $61$ and the product must be $122$ . Hence, our answer is $boxed{text{(B)} 1 }$ .
Each of the numbers $a$ and $b$ is a solution to $left| x - frac 1x right| = 1$ .Hence it is either a solution to $x - frac 1x = 1$ , or to $frac 1x - x = 1$ . Then it must be a solution either to $x^2 - x - 1 = 0$ , or to $x^2 + x - 1 = 0$ .There are in total four such values of $x$ , namely $frac{pm 1 pm sqrt 5}2$ .Out of these, two are positive: $frac{-1+sqrt 5}2$ and $frac{1+sqrt 5}2$ . We can easily check that both of them indeed have the required property, and their sum is $frac{-1+sqrt 5}2 + frac{1+sqrt 5}2 = boxed{(C) sqrt 5}$ .
First, note that $2002 = 11 cdot 13 cdot 14$ .Using the fact that for any base we have $log a + log b = log ab$ , we get that $N = log_{2002} (11^2 cdot 13^2 cdot 14^2) = log_{2002} 2002^2 = boxed{(D) N=2}$ .
As the unique mode is $8$ , there are at least two $8$ s.As the range is $8$ and one of the numbers is $8$ , the largest one can be at most $16$ .If the largest one is $16$ , then the smallest one is $8$ , and thus the mean is strictly larger than $8$ , which is a contradiction.If the largest one is $15$ , then the smallest one is $7$ . This means that we already know four of the values: $8$ , $8$ , $7$ , $15$ . Since the mean of all the numbers is $8$ , their sum must be $64$ . Thus the sum of the missing four numbers is $64-8-8-7-15=26$ . But if $7$ is the smallest number, then the sum of the missing numbers must be at least $4cdot 7=28$ , which is again a contradiction.If the largest number is $14$ , we can easily find the solution $(6,6,6,8,8,8,8,14)$ . Hence, our answer is $boxed{text{(D)} 14 }$ .

Note

The solution for $14$ is, in fact, unique. As the median must be $8$ , this means that both the $4^text{th}$ and the $5^text{th}$ number, when ordered by size, must be $8$ s. This gives the partial solution $(6,a,b,8,8,c,d,14)$ . For the mean to be $8$ each missing variable must be replaced by the smallest allowed value. The solution that works is $(6,6,6,8,8,8,8,14)$
Solution 1

This is not too bad using casework.

Tina gets a sum of 3: This happens in only one way $(1,2)$ and Sergio can choose a number from 4 to 10, inclusive. There are 7 ways that Sergio gets a desirable number here.

Tina gets a sum of 4: This once again happens in only one way $(1,3)$ . Sergio can choose a number from 5 to 10, so 6 ways here.

Tina gets a sum of 5: This can happen in two ways $(1,4)$ and $(2,3)$ . Sergio can choose a number from 6 to 10, so $2cdot5=10$ ways here.

Tina gets a sum of 6: Two ways here $(1,5)$ and $(2,4)$ . Sergio can choose a number from 7 to 10, so $2cdot4=8$ here.

Tina gets a sum of 7: Two ways here $(2,5)$ and $(3,4)$ . Sergio can choose from 8 to 10, so $2cdot3=6$ ways here.

Tina gets a sum of 8: Only one way possible $(3,5$ ). Sergio chooses 9 or 10, so 2 ways here.

Tina gets a sum of 9: Only one way $(4,5)$ . Sergio must choose 10, so 1 way.

In all, there are $7+6+10+8+6+2+1=40$ ways. Tina chooses two distinct numbers in $binom{5}{2}=10$ ways while Sergio chooses a number in $10$ ways, so there are $10cdot 10=100$ ways in all. Since $frac{40}{100}=frac{2}{5}$ , our answer is $boxed{text{(A)}frac{2}{5}}$ .

Solution 2

We want to find the average of the smallest possible chance of Sergio winning and the largest possible chance of Sergio winning. This is because the probability decreases linearly. The largest possibility of Sergio winning if Tina chooses a 1 and a 2. The chances of Sergio winning is then $frac{7}{10}$ . The smallest possibility of Sergio winning is if Tina chooses a 4 and a 5. The chances of Sergio winning then is $frac{1}{10}$ . The average of $frac{7}{10}$ and $frac{1}{10}$ is $boxed{text{(A)}frac{2}{5}}$ .

Solution 3

We invoke some symmetry. Let $T$ denote Tina's sum, and let $S$ denote Sergio's number. Observe that, for $i = 2, 3, ldots, 10$ , $text{Pr}(T=i) = text{Pr}(T=12-i)$ .

If Tina's sum is $i$ , then the probability that Sergio's number is larger than Tina's sum is $frac{10-i}{10}$ . Thus, the probability $P$ is

$[P = text{Pr}(S>T) = sum_{i=2}^{10} text{Pr}(T=i) times frac{10-i}{10}]$

Using the symmetry observation, we can also write the above sum as $[P = sum_{i=2}^{10} text{Pr}(T=12-i) times frac{10-i}{10} = sum_{i=2}^{10} text{Pr}(T=i) times frac{i-2}{10}]$ where the last equality follows as we reversed the indices of the sum (by replacing $12-i$ with $i$ ). Thus, adding the two equivalent expressions for $P$ , we have

$begin{align*} 2P &= sum_{i=2}^{10} text{Pr}(T=i) times left(frac{10-i}{10} + frac{i-2}{10}right) &= sum_{i=2}^{10} text{Pr}(T=i) times frac{4}{5} &= frac{4}{5} sum_{i=2}^{10} text{Pr}(T=i) &= frac{4}{5} end{align*}$

Since this represents twice the desired probability, the answer is $P = boxed{textbf{(A)} frac{2}{5}}$ .
Neither of the digits $4$ , $6$ , and $8$ can be a units digit of a prime. Therefore the sum of the set is at least $40 + 60 + 80 + 1 + 2 + 3 + 5 + 7 + 9 = 207$ .We can indeed create a set of primes with this sum, for example the following sets work: ${ 41, 67, 89, 2, 3, 5 }$ or ${ 43, 61, 89, 2, 5, 7 }$ .Thus the answer is $207implies boxed{mathrm{(B)}}$ .
Solution 1

(C) First examine the formula $(x-10)^2+y^2=36$ , for the circle $C_1$ . Its center, $D_1$ , is located at (10,0) and it has a radius of $sqrt{36}$ = 6. The next circle, using the same pattern, has its center, $D_2$ , at (-15,0) and has a radius of $sqrt{81}$ = 9. So we can construct this diagram: $[asy] unitsize(0.3cm); defaultpen(0.8); path C1=circle((10,0),6); path C2=circle((-15,0),9); draw(C1); draw(C2); draw( (-25,0) -- (17,0) ); dot((10,0)); dot((-15,0)); pair[] p1 = intersectionpoints(C1, circle((5,0),5) ); pair[] p2 = intersectionpoints(C2, circle((-7.5,0),7.5) ); dot(p1[1]); dot(p2[0]); draw((10,0)--p1[1]--p2[0]--(-15,0)); label("$C_1$",(10,0) + 6*dir(-45), SE ); label("$C_2$",(-15,0) + 9*dir(225), SW ); label("$D_1$",(10,0), SE ); label("$D_2$",(-15,0), SW ); label("$Q$", p2[0], NE ); label("$P$", p1[1], SW ); label("$O$", (0,0), SW ); [/asy]$ Line PQ is tangent to both circles, so it forms a right angle with the radii (6 and 9). This, as well as the two vertical angles near O, prove triangles S $_2$ QO and S $_1$ PO similar by AA, with a scale factor of 6:9, or 2:3. Next, we must subdivide the line D $_2$ D $_1$ in a 2:3 ratio to get the length of the segments D $_2$ O and D $_1$ O. The total length is 10 - (-15), or 25, so applying the ratio, D $_2$ O = 15 and D $_1$ O = 10. These are the hypotenuses of the triangles. We already know the length of D $_2$ Q and D $_1$ P, 9 and 6 (they're radii). So in order to find PQ, we must find the length of the longer legs of the two triangles and add them.

$15^2 - 9^2 = (15-9)(15+9) = 6 times 24 = 144$

$sqrt{144} = 12$

$10^2-6^2 = (10-6)(10+6) = 4 times 16 = 64$

$sqrt{64} = 8$

Finally, the length of PQ is $12+8=boxed{20}$ , or C.

Solution 2

Using the above diagram, imagine that segment $overline{QS_2}$ is shifted to the right to match up with $overline{PS_1}$ . Then shift $overline{QP}$ downwards to make a right triangle. We know $overline{S_2S_1} = 25$ from the given information and the newly created leg has length $overline{QS_2} + overline{PS_1} = 9 + 6 = 15$ . Hence by Pythagorean theorem $15^2 + {overline{QP}}^2 = 25^2$ .

$overline{QP} = boxed{20}$ , or C.
First of all, note that the equation $f(t)=6$ has two solutions: $t=-2$ and $t=1$ .Given an $x$ , let $f(x)=t$ . Obviously, to have $f(f(x))=6$ , we need to have $f(t)=6$ , and we already know when that happens. In other words, the solutions to $f(f(x))=6$ are precisely the solutions to ( $f(x)=-2$ or $f(x)=1$ ).Without actually computing the exact values, it is obvious from the graph that the equation $f(x)=-2$ has two and $f(x)=1$ has four different solutions, giving us a total of $2+4=boxed{(D)6}$ solutions. $[asy] size(200); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=4; pair P1=(-7,-4), P2=(-2,6), P3=(0,0), P4=(1,6), P5=(5,-6); real[] xticks={-7,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; real[] yticks={-6,-5,-4,-3,-2,-1,1,2,3,4,5,6}; path graph = P1--P2--P3--P4--P5; path line1 = (-7,1)--(6,1); path line2 = (-7,-2)--(6,-2); draw(graph); draw(line1, red); draw(line2, red); dot("(-7, -4)",P1); dot("(-2, 6)",P2,LeftSide); dot("(1, 6)",P4); dot("(5, -6)",P5); dot(intersectionpoints(graph,line1),red); dot(intersectionpoints(graph,line2),red); xaxis("$x$",-7.5,7,Ticks(xticks),EndArrow(6)); yaxis("$y$",-6.5,7,Ticks(yticks),EndArrow(6)); [/asy]$
Solution 1

The repeating decimal $0.overline{ab}$ is equal to $[frac{10a+b}{100} + frac{10a+b}{10000} + cdots = (10a+b)cdotleft(frac 1{10^2} + frac 1{10^4} + cdots right) = (10a+b) cdot frac 1{99} = frac{10a+b}{99}]$

When expressed in lowest terms, the denominator of this fraction will always be a divisor of the number $99 = 3cdot 3cdot 11$ . This gives us the possibilities ${1,3,9,11,33,99}$ . As $a$ and $b$ are not both nine and not both zero, the denominator $1$ can not be achieved, leaving us with $boxed{(C)5}$ possible denominators.

(The other ones are achieved e.g. for $ab$ equal to $33$ , $11$ , $9$ , $3$ , and $1$ , respectively.)

Solution 2

Another way to convert the decimal into a fraction (no idea what it's called). We have $[100(0.overline{ab}) = ab.overline{ab}]$ $[99(0.overline{ab}) = 100(0.overline{ab}) - 0.overline{ab} = ab.overline{ab} - 0.overline{ab} = ab]$ $[0.overline{ab} = frac{ab}{99}]$ where $a, b$ are digits. Continuing in the same way by looking at the factors of 99, we have 5 different possibilities for the denomenator. $boxed{(B)}$

~ Nafer

Solution 3

Since $frac{1}{99}=0.overline{01}$ , we know that $0.overline{ab} = frac{ab}{99}$ . From here, we wish to find the number of factors of $99$ , which is $6$ . However, notice that $1$ is not a possible denominator, so our answer is $6-1=boxed{5}$ .
The sequence is infinite. As there are only $100$ pairs of digits, sooner or later a pair of consecutive digits will occur for the second time. Aseach next digit only depends on the previous two, from this point on the sequence will be periodic.(Additionally, as every two consecutive digits uniquely determine the previous one as well, the first pair of digits that will occur twice must be the first pair $4,7$ .)Hence it is a good idea to find the period. Writing down more terms of the sequence, we get: $[4,7,1,8,9,7,6,3,9,2,1,3,4,7,dots]$ and we found the period. The length of the period is $12$ , and its sum is $4+7+cdots+1+3 = 60$ . Hence for each $k$ we have $S_{12k} = 60k$ .We have $lfloor 10000/60 rfloor = 166$ and $166cdot 12 = 1992$ , therefore $S_{1992} = 60cdot 166 = 9960$ . The rest can now be computed by hand, we get $S_{1998} = 9960+4+7+1+8+9+7= 9996$ , and $S_{1999}=9996 + 6 = 10002$ , thus the answer is $boxed{(B)1999}$ .
Clearly $BC=5$ and $AC=5sqrt{3}$ . Choose a $P'$ and get a corresponding $D'$ such that $BD'= 5sqrt{2}$ and $CD'=5$ . For $BD > 5sqrt2$ we need $CD>5$ , creating an isosceles right triangle with hyptenuse $5sqrt {2}$ . Thus the point $P$ may only lie in the triangle $ABD'$ . The probability of it doing so is the ratio of areas of $ABD'$ to $ABC$ , or equivalently, the ratio of $AD'$ to $AC$ because the triangles have identical altitudes when taking $AD'$ and $AC$ as bases. This ratio is equal to $frac{AC-CD'}{AC}=1-frac{CD'}{AC}=1-frac{5}{5sqrt{3}}=1-frac{sqrt{3}}{3}= frac{3-sqrt{3}}{3}$ . Thus the answer is $boxed{C}$
Solution 1 $[asy] unitsize(0.25 cm); pair A, B, C, D, M; A = (0,0); B = (88/9, 28*sqrt(5)/9); C = (16,0); D = 9/16*C; M = (B + C)/2; draw(A--B--C--cycle); draw(B--D--M); label("$A$", A, SW); label("$B$", B, N); label("$C$", C, SE); label("$D$", D, S); [/asy]$ Looking at the triangle $BCD$ , we see that its perpendicular bisector reaches the vertex, therefore implying it is isosceles. Let $x = angle C$ , so that $B=2x$ from given and the previous deducted. Then $angle ABD=x, angle ADB=2x$ because any exterior angle of a triangle has a measure that is the sum of the two interior angles that are not adjacent to the exterior angle. That means $triangle ABD$ and $triangle ACB$ are similar, so $frac {16}{AB}=frac {AB}{9} Longrightarrow AB=12$ .Then by using Heron's Formula on $ABD$ (with sides $12,7,9$ ), we have $[triangle ABD]= sqrt{14(2)(7)(5)} = 14sqrt5 Longrightarrow boxed{text{D}}$ .Solution 2Let M be the point of the perpendicular bisector on BC. By the perpendicular bisector theorem, $BD = DC = 7$ and $BM = MC$ . Also, by the angle bisector theorem, $frac {AB}{BC} = frac{9}{7}$ . Thus, let $AB = 9x$ and $BC = 7x$ . In addition, $BM = 3.5x$ .Thus, $cosangle CBD = frac {3.5x}{7} = frac {x}{2}$ . Additionally, using the Law of Cosines and the fact that $angle CBD = angle ABD$ , $81 = 49 + 81x^2 - 2(9x)(7)cosangle CBD$ Substituting and simplifying, we get $x = 4/3$ Thus, $AB = 12$ . We now know all sides of $triangle ABD$ . Using Heron's Formula on $triangle ABD$ , $sqrt{(14)(2)(7)(5)} = 14sqrt5 Longrightarrow boxed{text{D}}$ Solution 3Note that because the perpendicular bisector and angle bisector meet at side $AC$ and $CD = BD$ as triangle $BDC$ is isosceles, so $BD = 7$ . By the angle bisector theorem, we can express $AB$ and $BC$ as $9x$ and $7x$ respectively. We try to find $x$ through Stewart's Theorem. So
$16(7^2+9cdot7) = (7x)^2 cdot 9 + (9x)^2 cdot 7$

$16(49+63) = (49 cdot 9 + 81 cdot 7)x^2$

$16(49+63) = 9(49+63) cdot x^2$

$x^2 = frac{16}{9}$

$x=frac{4}{3}$

We plug this to find that the sides of $triangle ABD$ are $12,7,9$ . By Heron's formula, the area is $sqrt{(14)(2)(7)(5)} = 14sqrt5 Longrightarrow boxed{text{D}}$ .
Solution 1

Let $s=sqrt{a^2+b^2}$ be the magnitude of $a+bi$ . Then the magnitude of $(a+bi)^{2002}$ is $s^{2002}$ , while the magnitude of $a-bi$ is $s$ . We get that $s^{2002}=s$ , hence either $s=0$ or $s=1$ .

For $s=0$ we get a single solution $(a,b)=(0,0)$ .

Let's now assume that $s=1$ . Multiply both sides by $a+bi$ . The left hand side becomes $(a+bi)^{2003}$ , the right hand side becomes $(a-bi)(a+bi)=a^2 + b^2 = 1$ . Hence the solutions for this case are precisely all the $2003$ rd complex roots of unity, and there are $2003$ of those.

The total number of solutions is therefore $1+2003 = boxed{2004}$ .

Solution 2

As in the other solution, split the problem into when $s=0$ and when $s=1$ . When $s=1$ and $a+bi=costheta+isintheta$ ,

$(a+bi)^{2002}= cos(2002theta)+isin(2002theta)$ $=a-bi= costheta-isintheta= cos(-theta)+isin(-theta)$

so we must have $2002theta=-theta+2pi k$ and hence $theta=frac{2pi k}{2003}$ . Since $theta$ is restricted to $[0,2pi)$ , $k$ can range from $0$ to $2002$ inclusive, which is $2002-0+1=2003$ values. Thus the total is $1+2003 = boxed{textbf{(E)} 2004}$ .

Solution 3

Notice that r=0 or r=1 for this to be true. We know this because we are taking magnitude to the 2003rd power, and if the magnitude of a+bi is larger than 1, it will increase and if it is smaller than 1 it will decrease. However, the magnitude on the RHS is still r, so this is not possible. Again, only r=0 and r=1 satisfy.

Now if r=0, we must have (0,0) for (a,b). No exceptions.

However if r=1, we then have:

$cos(2002 theta) = cos(-theta)$ . This has solution of $theta = 0$ . This would represent the number 1+0i, with conjugate 1-0i. This works because the magnitude is the same and the angle is nothing anyways. We multiply angle by 2002 due to DeMoivre's Theorem and also we do $-theta$ because it is a reflection, angles therefore is negative.

We then write:

$cos(2002 theta) = cos(360-theta)$ which has solution of $theta = frac{360}{2003}$ .

We can also write:

$cos(2002 theta) = cos(720-theta)$ which has solution $theta = frac{720}{2003}$ .

We notice that it is simply headed upwards and the answer is of the form $frac{720}{2003} n$ , where n is some integer from 0 to infinity inclusive.

Well wait, it repeats itself n=2003, that is 360 which is also 0! Hence we only have n=0 to 2002 as original solutions, or 2003 solutions.

1+2003 = $boxed{2004}$ .
Solution 1

The sum of the coefficients of $P$ and of $Q$ will be equal, so $P(1) = Q(1)$ . The only answer choice with an intersection between the two graphs at $x = 1$ is $(B)$ . (The polynomials in the graph are $P(x) = 2x^4-3x^2-3x-4$ and $Q(x) = -2x^4-2x^2-2x-2$ .)

Solution 2

We know every coefficient is equal, so we get $ax^n + ... + ax + a = 0$ which equals $x^n + ... + x + 1 = 0$ . We see apparently that x cannot be positive, for it would yield a number greater than zero for $Q(x)$ . We look at the zeros of the answer choices. A, C, D, and E have a positive zero, which eliminates them. B is the answer.