Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2005AMC10A真题与答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月4日下午6:40

2005AMC10A真题

答案解析请参考文末

Problem 1

While eating out, Mike and Joe each tipped their server $2$ dollars. Mike tipped $10%$ of his bill and Joe tipped $20%$ of his bill. What was the difference, in dollars between their bills?

$mathrm{(A) } 2qquad mathrm{(B) } 4qquad mathrm{(C) } 5qquad mathrm{(D) } 10qquad mathrm{(E) } 20$

Problem 2

For each pair of real numbers $a neq b$ , define the operation $star$ as

$(a star b) = frac{a+b}{a-b}$ .

What is the value of $((1 star 2) star 3)$ ?

$mathrm{(A) } -frac{2}{3}qquad mathrm{(B) } -frac{1}{5}qquad mathrm{(C) } 0qquad mathrm{(D) } frac{1}{2}qquad mathrm{(E) } textrm{This, value, is, not, defined.}$

Problem 3

The equations $2x + 7 = 3$ and $bx - 10 = -2$ have the same solution $x$ . What is the value of $b$ ?

$mathrm{(A) } -8qquad mathrm{(B) } -4qquad mathrm{(C) } -2qquad mathrm{(D) } 4qquad mathrm{(E) } 8$

Problem 4

A rectangle with a diagonal of length $x$ is twice as long as it is wide. What is the area of the rectangle?

$mathrm{(A) } frac{1}{4}x^2qquad mathrm{(B) } frac{2}{5}x^2qquad mathrm{(C) } frac{1}{2}x^2qquad mathrm{(D) } x^2qquad mathrm{(E) } frac{3}{2}x^2$

Problem 5

A store normally sells windows at $100 each. This week the store is offering one free window for each purchase of four. Dave needs seven windows and Doug needs eight windows. How many dollars will they save if they purchase the windows together rather than separately?

$mathrm{(A) } 100qquad mathrm{(B) } 200qquad mathrm{(C) } 300qquad mathrm{(D) } 400qquad mathrm{(E) } 500$

Problem 6

The average (mean) of $20$ numbers is $30$ , and the average of $30$ other numbers is $20$ . What is the average of all $50$ numbers?

$mathrm{(A) } 23qquad mathrm{(B) } 24qquad mathrm{(C) } 25qquad mathrm{(D) } 26qquad mathrm{(E) } 27$

Problem 7

Josh and Mike live $13$ miles apart. Yesterday Josh started to ride his bicycle toward Mike's house. A little later Mike started to ride his bicycle toward Josh's house. When they met, Josh had ridden for twice the length of time as Mike and at four-fifths of Mike's rate. How many miles had Mike ridden when they met?

$mathrm{(A) } 4qquad mathrm{(B) } 5qquad mathrm{(C) } 6qquad mathrm{(D) } 7qquad mathrm{(E) } 8$

Problem 8

In the figure, the length of side $AB$ of square $ABCD$ is $sqrt{50}$ and $BE=1$ . What is the area of the inner square $EFGH$ ?

$textbf{(A)} 25qquadtextbf{(B)} 32qquadtextbf{(C)} 36qquadtextbf{(D)} 40qquadtextbf{(E)} 42$

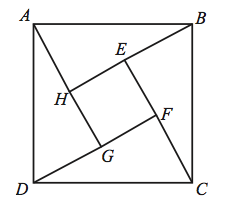
Problem 9

Three tiles are marked $X$ and two other tiles are marked $O$ . The five tiles are randomly arranged in a row. What is the probability that the arrangement reads $XOXOX$ ?

$mathrm{(A) } frac{1}{12}qquad mathrm{(B) } frac{1}{10}qquad mathrm{(C) } frac{1}{6}qquad mathrm{(D) } frac{1}{4}qquad mathrm{(E) } frac{1}{3}$

Problem 10

There are two values of $a$ for which the equation $4x^2 + ax + 8x + 9 = 0$ has only one solution for $x$ . What is the sum of those values of $a$ ?

$mathrm{(A) } -16qquad mathrm{(B) } -8qquad mathrm{(C) } 0qquad mathrm{(D) } 8qquad mathrm{(E) } 20$

Problem 11

A wooden cube $n$ units on a side is painted red on all six faces and then cut into $n^3$ unit cubes. Exactly one-fourth of the total number of faces of the unit cubes are red. What is $n$ ?

$mathrm{(A) } 3qquad mathrm{(B) } 4qquad mathrm{(C) } 5qquad mathrm{(D) } 6qquad mathrm{(E) } 7$

Problem 12

The figure shown is called a trefoil and is constructed by drawing circular sectors about the sides of the congruent equilateral triangles. What is the area of a trefoil whose horizontal base has length $2$ ?

$mathrm{(A) } frac{1}{3}pi+frac{sqrt{3}}{2}qquad mathrm{(B) } frac{2}{3}piqquad mathrm{(C) } frac{2}{3}pi+frac{sqrt{3}}{4}qquad mathrm{(D) } frac{2}{3}pi+frac{sqrt{3}}{3}qquad mathrm{(E) } frac{2}{3}pi+frac{sqrt{3}}{2}$

Problem 13

How many positive integers $n$ satisfy the following condition:

$(130n)^{50} > n^{100} > 2^{200}$ ?

$mathrm{(A) } 0qquad mathrm{(B) } 7qquad mathrm{(C) } 12qquad mathrm{(D) } 65qquad mathrm{(E) } 125$

Problem 14

How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?

$mathrm{(A) } 41qquad mathrm{(B) } 42qquad mathrm{(C) } 43qquad mathrm{(D) } 44qquad mathrm{(E) } 45$

Problem 15

How many positive cubes divide $3! cdot 5! cdot 7!$ ?

$mathrm{(A) } 2qquad mathrm{(B) } 3qquad mathrm{(C) } 4qquad mathrm{(D) } 5qquad mathrm{(E) } 6$

Problem 16

The sum of the digits of a two-digit number is subtracted from the number. The units digit of the result is $6$ . How many two-digit numbers have this property?

$mathrm{(A) } 5qquad mathrm{(B) } 7qquad mathrm{(C) } 9qquad mathrm{(D) } 10qquad mathrm{(E) } 19$

Problem 17

In the five-sided star shown, the letters $A$ , $B$ , $C$ , $D$ , and $E$ are replaced by the numbers $3$ , $5$ , $6$ , $7$ , and $9$ , although not necessarily in this order. The sums of the numbers at the ends of the line segments $AB$ , $BC$ , $CD$ , $DE$ , and $EA$ form an arithmetic sequence, although not necessarily in this order. What is the middle term of the sequence?

$mathrm{(A) } 9qquad mathrm{(B) } 10qquad mathrm{(C) } 11qquad mathrm{(D) } 12qquad mathrm{(E) } 13$

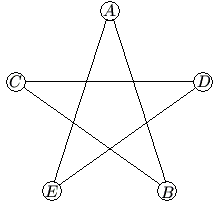
Problem 18

Team A and team B play a series. The first team to win three games wins the series. Each team is equally likely to win each game, there are no ties, and the outcomes of the individual games are independent. If team B wins the second game and team A wins the series, what is the probability that team B wins the first game?

$mathrm{(A) } frac{1}{5}qquad mathrm{(B) } frac{1}{4}qquad mathrm{(C) } frac{1}{3}qquad mathrm{(D) } frac{1}{2}qquad mathrm{(E) } frac{2}{3}$

Problem 19

Three one-inch squares are placed with their bases on a line. The center square is lifted out and rotated 45 degrees, as shown. Then it is centered and lowered into its original location until it touches both of the adjoining squares. How many inches is the point $B$ from the line on which the bases of the original squares were placed?

$[asy] unitsize(1inch); defaultpen(linewidth(.8pt)+fontsize(8pt)); draw((0,0)--((1/3) + 3*(1/2),0)); fill(((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6) + 1,(1/2))--((1/6) + 1,0)--cycle, rgb(.7,.7,.7)); draw(((1/6),0)--((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6),(1/2))--cycle); draw(((1/6) + (1/2),0)--((1/6) + (1/2),(1/2))--((1/6) + 1,(1/2))--((1/6) + 1,0)--cycle); draw(((1/6) + 1,0)--((1/6) + 1,(1/2))--((1/6) + (3/2),(1/2))--((1/6) + (3/2),0)--cycle); draw((2,0)--(2 + (1/3) + (3/2),0)); draw(((2/3) + (3/2),0)--((2/3) + 2,0)--((2/3) + 2,(1/2))--((2/3) + (3/2),(1/2))--cycle); draw(((2/3) + (5/2),0)--((2/3) + (5/2),(1/2))--((2/3) + 3,(1/2))--((2/3) + 3,0)--cycle); label("$B$",((1/6) + (1/2),(1/2)),NW); label("$B$",((2/3) + 2 + (1/4),(29/30)),NNE); draw(((1/6) + (1/2),(1/2)+0.05)..(1,.8)..((2/3) + 2 + (1/4)-.05,(29/30)),EndArrow(HookHead,3)); fill(((2/3) + 2 + (1/4),(1/4))--((2/3) + (5/2) + (1/10),(1/2) + (1/9))--((2/3) + 2 + (1/4),(29/30))--((2/3) + 2 - (1/10),(1/2) + (1/9))--cycle, rgb(.7,.7,.7)); draw(((2/3) + 2 + (1/4),(1/4))--((2/3) + (5/2) + (1/10),(1/2) + (1/9))--((2/3) + 2 + (1/4),(29/30))--((2/3) + 2 - (1/10),(1/2) + (1/9))--cycle);[/asy]$

$textbf{(A)} 1qquadtextbf{(B)} sqrt{2}qquadtextbf{(C)} frac{3}{2}qquadtextbf{(D)} sqrt{2}+frac{1}{2}qquadtextbf{(E)} 2$

Problem 20

An equiangular octagon has four sides of length 1 and four sides of length $frac{sqrt{2}}{2}$ , arranged so that no two consecutive sides have the same length. What is the area of the octagon?

$mathrm{(A) } frac72qquad mathrm{(B) } frac{7sqrt2}{2}qquad mathrm{(C) } frac{5+4sqrt2}{2}qquad mathrm{(D) } frac{4+5sqrt2}{2}qquad mathrm{(E) } 7$

Problem 21

For how many positive integers $n$ does $1+2+...+n$ evenly divide $6n$ ?

$mathrm{(A) } 3qquad mathrm{(B) } 5qquad mathrm{(C) } 7qquad mathrm{(D) } 9qquad mathrm{(E) } 11$

Problem 22

Let $S$ be the set of the $2005$ smallest positive multiples of $4$ , and let $T$ be the set of the $2005$ smallest positive multiples of $6$ . How many elements are common to $S$ and $T$ ?

$mathrm{(A) } 166qquad mathrm{(B) } 333qquad mathrm{(C) } 500qquad mathrm{(D) } 668qquad mathrm{(E) } 1001$

Problem 23

Let $AB$ be a diameter of a circle and let $C$ be a point on $AB$ with $2cdot AC=BC$ . Let $D$ and $E$ be points on the circle such that $DC perp AB$ and $DE$ is a second diameter. What is the ratio of the area of $triangle DCE$ to the area of $triangle ABD$ ?

$[asy] unitsize(2.5cm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0), C=(-1/3.0), B=(1,0), A=(-1,0); pair D=dir(aCos(C.x)), E=(-D.x,-D.y); draw(A--B--D--cycle); draw(D--E--C); draw(unitcircle,white); drawline(D,C); dot(O); clip(unitcircle); draw(unitcircle); label("$E$",E,SSE); label("$B$",B,E); label("$A$",A,W); label("$D$",D,NNW); label("$C$",C,SW); draw(rightanglemark(D,C,B,2));[/asy]$

$mathrm{(A) } frac{1}{6} qquad mathrm{(B) } frac{1}{4} qquad mathrm{(C) } frac{1}{3} qquad mathrm{(D) } frac{1}{2} qquad mathrm{(E) } frac{2}{3}$

Problem 24

For each positive integer $n > 1$ , let $P(n)$ denote the greatest prime factor of $n$ . For how many positive integers $n$ is it true that both $P(n) = sqrt{n}$ and $P(n+48) = sqrt{n+48}$ ?

$mathrm{(A) } 0qquad mathrm{(B) } 1qquad mathrm{(C) } 3qquad mathrm{(D) } 4qquad mathrm{(E) } 5$

Problem 25

In $ABC$ we have $AB = 25$ , $BC = 39$ , and $AC=42$ . Points $D$ and $E$ are on $AB$ and $AC$ respectively, with $AD = 19$ and $AE = 14$ . What is the ratio of the area of triangle $ADE$ to the area of the quadrilateral $BCED$ ?

$mathrm{(A) } frac{266}{1521}qquad mathrm{(B) } frac{19}{75}qquad mathrm{(C) } frac{1}{3}qquad mathrm{(D) } frac{19}{56}qquad mathrm{(E) } 1$

2005AMC10A详细解析

Let $m$ be Mike's bill and $j$ be Joe's bill. $frac{10}{100}m=2$ $m=20$ $frac{20}{100}j=2$ $j=10$ So the desired difference is $m-j=20-10=10 Rightarrow D$
$((1 star 2) star 3) = left(left(frac{1+2}{1-2}right) star 3right) = (-3 star 3) = frac{-3+3}{-3-3} = 0 Longrightarrow mathrm{(C)}$
$2x + 7 = 3 Longrightarrow x = -2, quad -2b - 10 = -2 Longrightarrow -2b = 8 Longrightarrow b = -4 mathrm{(B)}$
Let the width of the rectangle be $w$ . Then the length is $2w$ .Using the Pythagorean Theorem: $x^{2}=w^{2}+(2w)^{2}$ $x^{2}=5w^{2}$ The area of the rectangle is $2w^2=frac{2}{5}x^2$ $(B)$
The store's offer means that every $5$ th window is free.Dave would get $lfloorfrac{7}{5}rfloor=1$ free window.Doug would get $lfloorfrac{8}{5}rfloor=1$ free window.This is a total of $2$ free windows.Together, they would get $lfloorfrac{8+7}{5}rfloor = lfloorfrac{15}{5}rfloor=3$ free windows.So they get $3-2=1$ additional window if they purchase the windows together.Therefore they save $1cdot100=100Rightarrow A$
Since the average of the first $20$ numbers is $30$ , their sum is $20cdot30=600$ .Since the average of $30$ other numbers is $20$ , their sum is $30cdot20=600$ .So the sum of all $50$ numbers is $600+600=1200$ Therefore, the average of all $50$ numbers is $frac{1200}{50}=24 Longrightarrow mathrm{(B)}$
Let $m$ be the distance in miles that Mike rode.Since Josh rode for twice the length of time as Mike and at four-fifths of Mike's rate, he rode $2cdotfrac{4}{5}cdot m = frac{8}{5}m$ miles.Since their combined distance was $13$ miles, $frac{8}{5}m + m = 13$ $frac{13}{5}m = 13$ $m = 5 Longrightarrow mathrm{(B)}$
We see that side $BE$ , which we know is 1, is also the shorter leg of one of the four right triangles (which are congruent, I'll not prove this). So, $AH = 1$ . Then $HB = HE + BE = HE + 1$ , and $HE$ is one of the sides of the square whose area we want to find. So: $[1^2 + (HE+1)^2=sqrt{50}^2]$ $[1 + (HE+1)^2=50]$ $[(HE+1)^2=49]$ $[HE+1=7]$ $[HE=6]$ So, the area of the square is $6^2=boxed{36} Rightarrow mathrm{(C)}$ .
There are $frac{5!}{2!3!}=10$ distinct arrangements of three $X$ 's and two $O$ 's.There is only $1$ distinct arrangement that reads $XOXOX$ Therefore the desired probability is $boxed{frac{1}{10}} Rightarrow mathrm{(B)}$
A quadratic equation has exactly one root if and only if it is a perfect square. So set $4x^2 + ax + 8x + 9 = (mx + n)^2$ $4x^2 + ax + 8x + 9 = m^2x^2 + 2mnx + n^2$ Two polynomials are equal only if their coefficients are equal, so we must have $m^2 = 4, n^2 = 9$ $m = pm 2, n = pm 3$ $a + 8= 2mn = pm 2cdot 2cdot 3 = pm 12$ $a = 4$ or $a = -20$ .So the desired sum is $(4)+(-20)=-16 Longrightarrow mathrm{(A)}$ Alternatively, note that whatever the two values of $a$ are, they must lead to equations of the form $px^2 + qx + r =0$ and $px^2 - qx + r = 0$ . So the two choices of $a$ must make $a_1 + 8 = q$ and $a_2 + 8 = -q$ so $a_1 + a_2 + 16 = 0$ and $a_1 + a_2 = -16Longrightarrow mathrm{(A)}$ .
Since this quadratic must have a double root, the discriminant of the quadratic formula for this quadratic must be 0. Therefore, we must have $[(a+8)^2 - 4(4)(9) = 0 implies a^2 + 16a - 80.]$ We can use the quadratic formula to solve for its roots (we can ignore the things in the radical sign as they will cancel out due to the $pm$ sign when added). So we must have $[{-16 + sqrt{text{something}}}{2} + frac{-16 - sqrt{text{something}}}{2}.]$ Therefore, we have $implies boxed{A}$ .

There is only one positive value for k such that the quadratic equation would have only one solution. k-8 and -k-8 are the values of a.-8-8 is -16, so the answer is... $implies boxed{A}.$
Since there are $n^2$ little faces on each face of the big wooden cube, there are $6n^2$ little faces painted red.Since each unit cube has $6$ faces, there are $6n^3$ little faces total.Since one-fourth of the little faces are painted red, $frac{6n^2}{6n^3}=frac{1}{4}$ $frac{1}{n}=frac{1}{4}$ $n=4Longrightarrow mathrm{(B)}$
The area of the trefoil is equal to the area of a small equilateral triangle plus the area of four $60^circ$ sectors with a radius of $frac{2}{2}=1$ minus the area of a small equilateral triangle.This is equivalent to the area of four $60^circ$ sectors with a radius of $1$ .So the answer is: $4cdotfrac{60}{360}cdotpicdot1^2 = frac{4}{6}cdotpi = frac{2}{3}pi Rightarrow B$
We're given $(130n)^{50} > n^{100} > 2^{200}$ , so $sqrt[50]{(130n)^{50}} > sqrt[50]{n^{100}} > sqrt[50]{2^{200}}$ (because all terms are positive) and thus $130n > n^2 > 2^4$ $130n > n^2 > 16$ Solving each part separately: $n^2 > 16 Longrightarrow n > 4$ $130n > n^2 Longrightarrow 130 > n$ So $4 < n < 130$ .Therefore the answer is the number of positive integers over the interval $(4,130)$ which is $125 Longrightarrow mathrm{(E)}$ .
If the middle digit is the average of the first and last digits, twice the middle digit must be equal to the sum of the first and last digits.Doing some casework:If the middle digit is $1$ , possible numbers range from $111$ to $210$ . So there are $2$ numbers in this case.If the middle digit is $2$ , possible numbers range from $123$ to $420$ . So there are $4$ numbers in this case.If the middle digit is $3$ , possible numbers range from $135$ to $630$ . So there are $6$ numbers in this case.If the middle digit is $4$ , possible numbers range from $147$ to $840$ . So there are $8$ numbers in this case.If the middle digit is $5$ , possible numbers range from $159$ to $951$ . So there are $9$ numbers in this case.If the middle digit is $6$ , possible numbers range from $369$ to $963$ . So there are $7$ numbers in this case.If the middle digit is $7$ , possible numbers range from $579$ to $975$ . So there are $5$ numbers in this case.If the middle digit is $8$ , possible numbers range from $789$ to $987$ . So there are $3$ numbers in this case.
If the middle digit is $9$ , the only possible number is $999$ . So there is $1$ number in this case.

So the total number of three-digit numbers that satisfy the property is $2+4+6+8+9+7+5+3+1=45Rightarrow E$

Alternatively, we could note that the middle digit is uniquely defined by the first and third digits since it is half of their sum. This also means that the sum of the first and third digits must be even. Since even numbers are formed either by adding two odd numbers or two even numbers, we can split our problem into 2 cases:

If both the first digit and the last digit are odd, then we have 1, 3, 5, 7, or 9 as choices for each of these digits, and there are $5cdot5=25$ numbers in this case.

If both the first and last digits are even, then we have 2, 4, 6, 8 as our choices for the first digit and 0, 2, 4, 6, 8 for the third digit. There are $4cdot5=20$ numbers here.

The total number, then, is $20+25=45Rightarrow E$
$3! cdot 5! cdot 7! = (3cdot2cdot1) cdot (5cdot4cdot3cdot2cdot1) cdot (7cdot6cdot5cdot4cdot3cdot2cdot1) = 2^{8}cdot3^{4}cdot5^{2}cdot7^{1}$ Therefore, a perfect cube that divides $3! cdot 5! cdot 7!$ must be in the form $2^{a}cdot3^{b}cdot5^{c}cdot7^{d}$ where $a$ , $b$ , $c$ , and $d$ are nonnegative multiples of $3$ that are less than or equal to $8$ , $5$ , $2$ and $1$ , respectively.So: $ain{0,3,6}$ ( $3$ possibilities) $bin{0,3}$ ( $2$ possibilities) $cin{0}$ ( $1$ possibility) $din{0}$ ( $1$ possibility)So the number of perfect cubes that divide $3! cdot 5! cdot 7!$ is $3cdot2cdot1cdot1 = 6 Rightarrow mathrm{(E)}$ $3! cdot 5! cdot 7! = (3cdot2cdot1) cdot (5cdot4cdot3cdot2cdot1) cdot (7cdot6cdot5cdot4cdot3cdot2cdot1)$ In the expression, we notice that there are 3 $3's$ , 3 $2's$ , and 3 $1's$ . This gives us our first 3 cubes: $3^3$ , $2^3$ , and $1^3$ .
However, we can also multiply smaller numbers in the expression to make bigger expressions. For example, $(2*2)*4*4=4*4*4=4^3$ (one 2 comes from the $3!$ , and the other from the $5!$ ). Using this method, we find:

$(3*2)*(3*2)*6=6^3$

and

$(3*4)*(3*4)*(2*6)=12^3$

So, we have 6 cubes total: $1^3 ,2^3, 3^3, 4^3, 6^3,$ and $12^3$ for a total of $6$ cubes $Rightarrow mathrm{(E)}$
Let the number be $10a+b$ where $a$ and $b$ are the tens and units digits of the number.So $(10a+b)-(a+b)=9a$ must have a units digit of $6$ This is only possible if $9a=36$ , so $a=4$ is the only way this can be true.So the numbers that have this property are $40$ , $41$ , $42$ , $43$ , $44$ , $45$ , $46$ , $47$ , $48$ , $49$ .Therefore the answer is $10Rightarrow D$
Each corner (a,b,c,d,e) goes to two sides/numbers. (A goes to AE and AB, D goes to DC and DE). The sum of every term is equal to $2005AMC10A真题与答案解析$ Since the middle term in an arithmetic sequence is the average of all the terms in the sequence, the middle number is $frac{60}{5}=12Rightarrow D$
There are at most $5$ games played.If team B won the first two games, team A would need to win the next three games. So the only possible order of wins is BBAAA.If team A won the first game, and team B won the second game, the possible order of wins are: ABBAA, ABABA, and ABAAX, where X denotes that the 5th game wasn't played.Since ABAAX is dependent on the outcome of $4$ games instead of $5$ , it is twice as likely to occur and can be treated as two possibilities.Since there is $1$ possibility where team B wins the first game and $5$ total possibilities, the desired probability is $frac{1}{5}Rightarrow A$
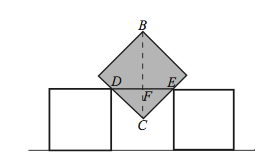Consider the rotated middle square shown in the figure. It will drop until length $DE$ is 1 inch. Then, because $DEC$ is a $45^{circ}-45^{circ}-90^{circ}$ triangle, $EC=frac{sqrt{2}}{2}$ , and $FC=frac{1}{2}$ . We know that $BC=sqrt{2}$ , so the distance from $B$ to the line is $BC-FC+1=sqrt{2}-frac{1}{2}+1=sqrt{2}+dfrac{1}{2}$ $(D)$ .(Refer to Diagram Above)After deducing that $BC=sqrt{2}$ , we can observe that the length from $C$ to the baseline is $frac{1}{2}$ . This can be obtained by subtracting $FC$ from the side length of the square(s), which is $1$ .Adding these up, we see that our answer is $(D)$ $sqrt{2}+dfrac{1}{2}$ .
The area of the octagon can be divided up into 5 squares with side $frac{sqrt2}2$ and 4 right triangles, which are half the area of each of the squares.Therefore, the area of the octagon is equal to the area of $5+4left(frac12right)=7$ squares.The area of each square is $left(frac{sqrt2}2right)^2=frac12$ , so the area of 7 squares is $frac72Rightarrowmathrm{(A)}$ . $[asy] pair A=(0.5, 0), B=(0, 0.5), C=(0, 1.5), D=(0.5, 2), E=(1.5, 2), F=(2, 1.5), G=(2, 0.5), H=(1.5, 0); draw(A--B); draw(B--C); draw(C--D); draw(D--E);draw(E--F);draw(F--G); draw(G--H); draw(H--A);draw(A--F, blue);draw(E--B,blue);draw(C--H, blue); draw(D--G,blue);dot(A);dot(B);dot(C);dot(D);dot(E);dot(F);dot(G);dot(H); [/asy]$ Using the diagram from above, we can extend the sides of length $1$ to form four right triangles and the octagon, all inside a square. The right triangles are 45-45-90 triangles with hypotenuse $frac{sqrt{2}}{2}$ , so the side length is $frac{1}{2}$ . Thus, the area of the larger square is $2 cdot 2 = 4$ , and the area of the four right triangles combined is $frac{1}{2}$ , so the area of the octagon is $frac{7}{2}$ , or $boxed{mathrm{(A). }}$
If $1+2+...+n$ evenly divides $6n$ , then $frac{6n}{1+2+...+n}$ is an integer.Since $1+2+...+n = frac{n(n+1)}{2}$ we may substitute the RHS in the above fraction. So the problem asks us for how many positive integers $n$ is $frac{6n}{frac{n(n+1)}{2}}=frac{12}{n+1}$ an integer, or equivalently when $k(n+1) = 12$ for a positive integer $k$ . $frac{12}{n+1}$ is an integer when $n+1$ is a factor of $12$ .The factors of $12$ are $1$ , $2$ , $3$ , $4$ , $6$ , and $12$ , so the possible values of $n$ are $0$ , $1$ , $2$ , $3$ , $5$ , and $11$ .But $0$ isn't a positive integer, so only $1$ , $2$ , $3$ , $5$ , and $11$ are possible values of $n$ . Therefore the number of possible values of $n$ is $5Longrightarrow boxed{mathrm{(B)}}$ .
Since the least common multiple $mathrm{lcm}(4,6)=12$ , the elements that are common to $S$ and $T$ must be multiples of $12$ .Since $4cdot2005=8020$ and $6cdot2005=12030$ , several multiples of $12$ that are in $T$ won't be in $S$ , but all multiples of $12$ that are in $S$ will be in $T$ . So we just need to find the number of multiples of $12$ that are in $S$ .Since $4cdot3=12$ every $3$ rd element of $S$ will be a multiple of $12$ Therefore the answer is $lfloorfrac{2005}{3}rfloor=668Longrightarrow boxed{mathrm{(D) 668}}$
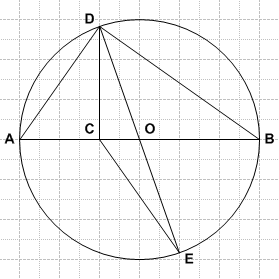Let us assume that the diameter is of length $1$ . $AC$ is $frac{1}{3}$ of diameter and $CO$ is $frac{1}{2}-frac{1}{3} = frac{1}{6}$ . $OD$ is the radius of the circle, so using the Pythagorean theorem height $CD$ of $triangle DCO$ is $sqrt{left(frac{1}{2}right)^2-left(frac{1}{6}right)^2} = frac{sqrt{2}}{3}$ . This is also the height of the $triangle ABD$ .Area of the $triangle DCO$ is $frac{1}{2}cdotfrac{1}{6}cdotfrac{sqrt{2}}{3}$ = $frac{sqrt{2}}{36}$ .The height of $triangle DCE$ can be found using the area of $triangle DCO$ and $DO$ as base.Hence the height of $triangle DCE$ is $dfrac{dfrac{sqrt{2}}{36}}{dfrac{1}{2}cdotdfrac{1}{2}}$ = $dfrac{sqrt{2}}{9}$ .The diameter is the base for both the triangles $triangle DCE$ and $triangle ABD$ .Hence, the ratio of the area of $triangle DCE$ to the area of $triangle ABD$ is $dfrac{dfrac{sqrt{2}}{9}}{dfrac{sqrt{2}}{3}}$ = $dfrac{1}{3} Rightarrow C$ Since $triangle DCE$ and $triangle ABD$ share a base, the ratio of their areas is the ratio of their altitudes. Draw the altitude from $C$ to $DE$ .
$[asy] import graph; import olympiad; pair O,A,B,C,D,E,F; O=(0,0);A=(15,0);B=(-15,0);C=(5,0);D=(5,14.142135623730950488016887242097);E=(-5,-14.142135623730950488016887242097);F=(0.5555555555555555,1.5713484026367722764463208046774); draw(Circle((0,0),15)); draw(A--B);draw(D--E);draw(C--D);draw(C--E);draw(C--F);draw(A--D);draw(D--B); label("A",A,NE);label("B",B,W);label("C",C,SE);label("D",D,NE);label("E",E,SW);label("O",O,SW);label("F",F,NW); markscalefactor=0.2; draw(anglemark(C,F,D),blue);draw(anglemark(D,C,B),blue); [/asy]$ $OD=r, OC=frac{1}{3}r$ .

Since $mangle DCO=mangle DFC=90^circ$ , then $triangle DCOcong triangle DFC$ . So the ratio of the two altitudes is $frac{CF}{DC}=frac{OC}{DO}=frac{1}{3}Rightarrow text{(C)}$

Say the center of the circle is point $O$ ; Without loss of generality, assume $AC=2$ , so $CB=4$ and the diameter and radius are $6$ and $3$ , respectively. Therefore, $CO=1$ , and $DO=3$ . The area of $triangle DCE$ can be expressed as $frac{1}{2}(CD)(6)text{sin }(CDE).$ $frac{1}{2}(CD)(6)$ happens to be the area of $triangle ABD$ . Furthermore, $text{sin } CDE = frac{CO}{DO},$ or $frac{1}{3}.$ Therefore, the ratio is $frac{1}{3}.$

WLOG, let $AC=1$ , $BC=2$ , so radius of the circle is $frac{3}{2}$ and $OC=frac{1}{2}$ . As in solution 1, By same altitude, the ratio $[DCE]/[ABD]=PE/AB$ , where $P$ is the point where $DC$ extended meets circle $O$ . Note that angle P = 90 deg, so DCO ~ DPE with ratio 1:2, so PE = 1. Thus, our ratio is $frac{1}{3}$ .
If $P(n) = sqrt{n}$ , then $n = p_{1}^{2}$ , where $p_{1}$ is a prime number.If $P(n+48) = sqrt{n+48}$ , then $n+48 = p_{2}^{2}$ , where $p_{2}$ is a different prime number.So: $p_{2}^{2} = n+48$ $p_{1}^{2} = n$ $p_{2}^{2} - p_{1}^{2} = 48$ $(p_{2}+p_{1})(p_{2}-p_{1})=48$ Since $p_{1} > 0$ : $(p_{2}+p_{1}) > (p_{2}-p_{1})$ .Looking at pairs of divisors of $48$ , we have several possibilities to solve for $p_{1}$ and $p_{2}$ : $(p_{2}+p_{1}) = 48$
$(p_{2}-p_{1}) = 1$

$p_{1} = frac{47}{2}$

$p_{2} = frac{49}{2}$

$(p_{2}+p_{1}) = 24$

$(p_{2}-p_{1}) = 2$

$p_{1} = 11$

$p_{2} = 13$

$(p_{2}+p_{1}) = 16$

$(p_{2}-p_{1}) = 3$

$p_{1} = frac{13}{2}$

$p_{2} = frac{19}{2}$

$(p_{2}+p_{1}) = 12$

$(p_{2}-p_{1}) = 4$

$p_{1} = 4$

$p_{2} = 8$

$(p_{2}+p_{1}) = 8$

$(p_{2}-p_{1}) = 6$

$p_{1} = 1$

$p_{2} = 7$

The only solution $(p_{1} , p_{2})$ where both numbers are primes is $(11,13)$ .

Therefore the number of positive integers $n$ that satisfy both statements is $1Rightarrow mathrm{(B)}$
We have that $[frac{[ADE]}{[ABC]} = frac{AD}{AB} cdot frac{AE}{AC} = frac{19}{25} cdot frac{14}{42} = frac{19}{75}.]$ $[asy] unitsize(0.15 cm); pair A, B, C, D, E; A = (191/39,28*sqrt(1166)/39); B = (0,0); C = (39,0); D = (6*A + 19*B)/25; E = (28*A + 14*C)/42; draw(A--B--C--cycle); draw(D--E); label("$A$", A, N); label("$B$", B, SW); label("$C$", C, SE); label("$D$", D, W); label("$E$", E, NE); label("$19$", (A + D)/2, W); label("$6$", (B + D)/2, W); label("$14$", (A + E)/2, NE); label("$28$", (C + E)/2, NE); [/asy]$ But $[BCED] = [ABC] - [ADE]$ , so $begin{align*} frac{[ADE]}{[BCED]} &= frac{[ADE]}{[ABC] - [ADE]} \ &= frac{1}{[ABC]/[ADE] - 1} \ &= frac{1}{75/19 - 1} \ &= boxed{frac{19}{56}Longrightarrow D}. end{align*}$ We can let $[ADE]=x$ . Since $EC=2*EA$ , $[DEC]=2x$ . So, $[ADC]=3x$ . This means that $[BDC]=frac{6}{19}cdot3x=frac{18x}{19}$ . Thus, $[frac{[ADE]}{[BCED]} = frac{x}{frac{18x}{19}+2x}= boxed{frac{19}{56}Longrightarrow D}.]$ -Conantwiz2023The area of a triangle is $frac{1}{2}bcsin A$ .Using this formula: $[ADE]=frac{1}{2}cdot19cdot14cdotsin A = 133sin A$ $[ABC]=frac{1}{2}cdot25cdot42cdotsin A = 525sin A$ Since the area of $BCED$ is equal to the area of $ABC$ minus the area of $ADE$ ,
$[BCED] = 525sin A - 133sin A = 392sin A$ .

Therefore, the desired ratio is $frac{133sin A}{392sin A}=frac{19}{56}Longrightarrow mathrm{(D)}$