Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

2007AMC10A真题与答案解析

Category: AMC美国数学竞赛, 国际竞赛 Date: 2019年12月4日下午5:36

2007AMC10A真题

答案解析请参考文末

Problem 1

One ticket to a show costs $$20$ at full price. Susan buys 4 tickets using a coupon that gives her a $25%$ discount. Pam buys 5 tickets using a coupon that gives her a $30%$ discount. How many more dollars does Pam pay than Susan?

$mathrm{(A)} 2qquad mathrm{(B)} 5qquad mathrm{(C)} 10qquad mathrm{(D)} 15qquad mathrm{(E)} 20$

Problem 2

Define $a@b = ab - b^{2}$ and $a#b = a + b - ab^{2}$ . What is $frac {6@2}{6#2}$ ?

$text{(A)} - frac {1}{2}qquad text{(B)} - frac {1}{4}qquad text{(C)} frac {1}{8}qquad text{(D)} frac {1}{4}qquad text{(E)} frac {1}{2}$

Problem 3

An aquarium has a rectangular base that measures 100 cm by 40 cm and has a height of 50 cm. It is filled with water to a height of 40 cm. A brick with a rectangular base that measures 40 cm by 20 cm and a height of 10 cm is placed in the aquarium. By how many centimeters does the water rise?

$text{(A)} 0.5 qquad text{(B)} 1 qquad text{(C)} 1.5 qquad text{(D)} 2 qquad text{(E)} 2.5$

Problem 4

The larger of two consecutive odd integers is three times the smaller. What is their sum?

$text{(A)} 4 qquad text{(B)} 8 qquad text{(C)} 12 qquad text{(D)} 16 qquad text{(E)} 20$

Problem 5

A school store sells 7 pencils and 8 notebooks for $$4.15$ . It also sells 5 pencils and 3 notebooks for $$1.77$ . How much do 16 pencils and 10 notebooks cost?

$text{(A)} $1.76 qquad text{(B)} $5.84 qquad text{(C)} $6.00 qquad text{(D)} $6.16 qquad text{(E)} $6.32$

Problem 6

At Euclid High School, the number of students taking the AMC 10 was $60$ in 2002, $66$ in 2003, $70$ in 2004, $76$ in 2005, $78$ in 2006, and is $85$ in 2007. Between what two consecutive years was there the largest percentage increase?

$text{(A)} 2002 text{and} 2003 qquad text{(B)} 2003 text{and} 2004 qquad text{(C)} 2004 text{and} 2005 qquad text{(D)} 2005 text{and} 2006 qquad text{(E)} 2006 text{and} 2007$

Problem 7

Last year Mr. Jon Q. Public received an inheritance. He paid $20%$ in federal taxes on the inheritance, and paid $10%$ of what he had left in state taxes. He paid a total of $10500$ for both taxes. How many dollars was his inheritance?

$(mathrm {A}) 30000 qquad (mathrm {B}) 32500 qquad(mathrm {C}) 35000 qquad(mathrm {D}) 37500 qquad(mathrm {E}) 40000$

Problem 8

Triangles $ABC$ and $ADC$ are isosceles with $AB=BC$ and $AD=DC$ . Point $D$ is inside triangle $ABC$ , angle $ABC$ measures 40 degrees, and angle $ADC$ measures 140 degrees. What is the degree measure of angle $BAD$ ?

$mathrm{(A)} 20qquad mathrm{(B)} 30qquad mathrm{(C)} 40qquad mathrm{(D)} 50qquad mathrm{(E)} 60$

Problem 9

Real numbers $a$ and $b$ satisfy the equations $3^{a} = 81^{b + 2}$ and $125^{b} = 5^{a - 3}$ . What is $ab$ ?

$text{(A)} -60 qquad text{(B)} -17 qquad text{(C)} 9 qquad text{(D)} 12 qquad text{(E)} 60$

Problem 10

The Dunbar family consists of a mother, a father, and some children. The average age of the members of the family is $20$ , the father is $48$ years old, and the average age of the mother and children is $16$ . How many children are in the family?

$text{(A)} 2 qquad text{(B)} 3 qquad text{(C)} 4 qquad text{(D)} 5 qquad text{(E)} 6$

Problem 11

The numbers from $1$ to $8$ are placed at the vertices of a cube in such a manner that the sum of the four numbers on each face is the same. What is this common sum?

$text{(A)} 14 qquad text{(B)} 16 qquad text{(C)} 18 qquad text{(D)} 20 qquad text{(E)} 24$

Problem 12

Two tour guides are leading six tourists. The guides decide to split up. Each tourist must choose one of the guides, but with the stipulation that each guide must take at least one tourist. How many different groupings of guides and tourists are possible?

$text{(A)} 56 qquad text{(B)} 58 qquad text{(C)} 60 qquad text{(D)} 62 qquad text{(E)} 64$

Problem 13

Yan is somewhere between his home and the stadium. To get to the stadium he can walk directly to the stadium, or else he can walk home and then ride his bicycle to the stadium. He rides 7 times as fast as he walks, and both choices require the same amount of time. What is the ratio of Yan's distance from his home to his distance from the stadium?

$mathrm{(A)} frac 23qquad mathrm{(B)} frac 34qquad mathrm{(C)} frac 45qquad mathrm{(D)} frac 56qquad mathrm{(E)} frac 78$

Problem 14

A triangle with side lengths in the ratio $3 : 4 : 5$ is inscribed in a circle with radius $3$ . What is the area of the triangle?

$mathrm{(A)} 8.64qquad mathrm{(B)} 12qquad mathrm{(C)} 5piqquad mathrm{(D)} 17.28qquad mathrm{(E)} 18$

Problem 15

Four circles of radius $1$ are each tangent to two sides of a square and externally tangent to a circle of radius $2$ , as shown. What is the area of the square?

$[asy] unitsize(5mm); defaultpen(linewidth(.8pt)+fontsize(8pt)); real h=3*sqrt(2)/2; pair O0=(0,0), O1=(h,h), O2=(-h,h), O3=(-h,-h), O4=(h,-h); pair X=O0+2*dir(30), Y=O2+dir(45); draw((-h-1,-h-1)--(-h-1,h+1)--(h+1,h+1)--(h+1,-h-1)--cycle); draw(Circle(O0,2)); draw(Circle(O1,1)); draw(Circle(O2,1)); draw(Circle(O3,1)); draw(Circle(O4,1)); draw(O0--X); draw(O2--Y); label("$2$",midpoint(O0--X),NW); label("$1$",midpoint(O2--Y),SE); [/asy]$ $text{(A)} 32 qquad text{(B)} 22 + 12sqrt {2}qquad text{(C)} 16 + 16sqrt {3}qquad text{(D)} 48 qquad text{(E)} 36 + 16sqrt {2}$

Problem 16

Integers $a, b, c,$ and $d$ , not necessarily distinct, are chosen independently and at random from 0 to 2007, inclusive. What is the probability that $ad-bc$ is even?

$mathrm{(A)} frac 38qquad mathrm{(B)} frac 7{16}qquad mathrm{(C)} frac 12qquad mathrm{(D)} frac 9{16}qquad mathrm{(E)} frac 58$

Problem 17

Suppose that $m$ and $n$ are positive integers such that $75m = n^{3}$ . What is the minimum possible value of $m + n$ ?

$text{(A)} 15 qquad text{(B)} 30 qquad text{(C)} 50 qquad text{(D)} 60 qquad text{(E)} 5700$

Problem 18

Consider the $12$ -sided polygon $ABCDEFGHIJKL$ , as shown. Each of its sides has length $4$ , and each two consecutive sides form a right angle. Suppose that $overline{AG}$ and $overline{CH}$ meet at $M$ . What is the area of quadrilateral $ABCM$ ?

$[asy] unitsize(13mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=4; pair A=(1,3), B=(2,3), C=(2,2), D=(3,2), Ep=(3,1), F=(2,1), G=(2,0), H=(1,0), I=(1,1), J=(0,1), K=(0,2), L=(1,2); pair M=intersectionpoints(A--G,H--C)[0]; draw(A--B--C--D--Ep--F--G--H--I--J--K--L--cycle); draw(A--G); draw(H--C); dot(M); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,NE); label("$D$",D,NE); label("$E$",Ep,SE); label("$F$",F,SE); label("$G$",G,SE); label("$H$",H,SW); label("$I$",I,SW); label("$J$",J,SW); label("$K$",K,NW); label("$L$",L,NW); label("$M$",M,W); [/asy]$ $text{(A)} frac {44}{3}qquad text{(B)} 16 qquad text{(C)} frac {88}{5}qquad text{(D)} 20 qquad text{(E)} frac {62}{3}$

Problem 19

A paint brush is swept along both diagonals of a square to produce the symmetric painted area, as shown. Half the area of the square is painted. What is the ratio of the side length of the square to the brush width?

$[asy] unitsize(15mm); defaultpen(linewidth(.8pt)); path P=(-sqrt(2)/2,1)--(0,1-sqrt(2)/2)--(sqrt(2)/2,1); path Pc=(-sqrt(2)/2,1)--(0,1-sqrt(2)/2)--(sqrt(2)/2,1)--cycle; path S=(-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle; fill(S,gray); for(int i=0;i<4;++i) { fill(rotate(90*i)*Pc,white); draw(rotate(90*i)*P); } draw(S); [/asy]$ $text{(A)} 2sqrt {2} + 1 qquad text{(B)} 3sqrt {2}qquad text{(C)} 2sqrt {2} + 2 qquad text{(D)} 3sqrt {2} + 1 qquad text{(E)} 3sqrt {2} + 2$

Problem 20

Suppose that the number $a$ satisfies the equation $4 = a + a^{ - 1}$ . What is the value of $a^{4} + a^{ - 4}$ ?

$text{(A)} 164 qquad text{(B)} 172 qquad text{(C)} 192 qquad text{(D)} 194 qquad text{(E)} 212$

Problem 21

A sphere is inscribed in a cube that has a surface area of $24$ square meters. A second cube is then inscribed within the sphere. What is the surface area in square meters of the inner cube?

$text{(A)} 3 qquad text{(B)} 6 qquad text{(C)} 8 qquad text{(D)} 9 qquad text{(E)} 12$

Problem 22

A finite sequence of three-digit integers has the property that the tens and units digits of each term are, respectively, the hundreds and tens digits of the next term, and the tens and units digits of the last term are, respectively, the hundreds and tens digits of the first term. For example, such a sequence might begin with the terms 247, 475, and 756 and end with the term 824. Let $S$ be the sum of all the terms in the sequence. What is the largest prime factor that always divides $S$ ?

$mathrm{(A)} 3qquad mathrm{(B)} 7qquad mathrm{(C)} 13qquad mathrm{(D)} 37qquad mathrm{(E)} 43$

Problem 23

How many ordered pairs $(m,n)$ of positive integers, with $m ge n$ , have the property that their squares differ by $96$ ?

$text{(A)} 3 qquad text{(B)} 4 qquad text{(C)} 6 qquad text{(D)} 9 qquad text{(E)} 12$

Problem 24

Circles centered at $A$ and $B$ each have radius $2$ , as shown. Point $O$ is the midpoint of $overline{AB}$ , and $OA = 2sqrt {2}$ . Segments $OC$ and $OD$ are tangent to the circles centered at $A$ and $B$ , respectively, and $EF$ is a common tangent. What is the area of the shaded region $ECODF$ ?

$[asy] unitsize(6mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0); pair A=(-2*sqrt(2),0); pair B=(2*sqrt(2),0); pair G=shift(0,2)*A; pair F=shift(0,2)*B; pair C=shift(A)*scale(2)*dir(45); pair D=shift(B)*scale(2)*dir(135); pair X=A+2*dir(-60); pair Y=B+2*dir(240); path P=C--O--D--Arc(B,2,135,90)--G--Arc(A,2,90,45)--cycle; fill(P,gray); draw(Circle(A,2)); draw(Circle(B,2)); dot(A); label("$A$",A,W); dot(B); label("$B$",B,E); dot(C); label("$C$",C,W); dot(D); label("$D$",D,E); dot(G); label("$E$",G,N); dot(F); label("$F$",F,N); dot(O); label("$O$",O,S); draw(G--F); draw(C--O--D); draw(A--B); draw(A--X); draw(B--Y); label("$2$",midpoint(A--X),SW); label("$2$",midpoint(B--Y),SE); [/asy]$ $text{(A)} frac {8sqrt {2}}{3} qquad text{(B)} 8sqrt {2} - 4 - pi qquad text{(C)} 4sqrt {2} qquad text{(D)} 4sqrt {2} + frac {pi}{8} qquad text{(E)} 8sqrt {2} - 2 - frac {pi}{2}$

Problem 25

For each positive integer $n$ , let $S(n)$ denote the sum of the digits of $n.$ For how many values of $n$ is $n + S(n) + S(S(n)) = 2007?$

$mathrm{(A)} 1 qquad mathrm{(B)} 2 qquad mathrm{(C)} 3 qquad mathrm{(D)} 4 qquad mathrm{(E)} 5$

2007AMC10A详细解析

= the amount Pam spent = the amount Susan spent
- $P=5 cdot (20 cdot .7) = 70$
- $S=4 cdot (20 cdot .75) = 60$
Pam pays 10 more dollars than Susan $Rightarrowfbox{C}$
$[frac{6 @ 2}{6 # 2} = frac{(6)times (2) - (2)^2}{(6) + (2) - (6) cdot (2)^2} = frac{8}{-16} = frac{-1}{2} Rightarrow mathrm{(A)}]$
The volume of the brick is $40 times 20 times 10 = 8000$ . Thus the water volume rose $8000 = 100 times 40 times h Longrightarrow h = 2 mathrm{(D)}$ .
Let the two consecutive odd integers be $a$ , $a+2$ . Then $a+2 = 3a$ , so $a = 1$ and their sum is $4 mathrm{(A)}$ .
We let $p =$ cost of pencils in cents, $n =$ number of notebooks in cents. Then $begin{align*} 7p + 8n = 415 &Longrightarrow 35p + 40n = 2075\ 5p + 3n = 177 &Longrightarrow 35p + 21n = 1239 end{align*}$ Subtracting these equations yields $19n = 836 Longrightarrow n = 44$ . Backwards solving gives $p = 9$ . Thus the answer is $16p + 10n = 584 mathrm{(B)}$ .
We compute the percentage increases:
1. $frac{66 - 60}{60} = 10%$
2. $frac{70 - 66}{66} approx 6%$
3. $frac{76-70}{70} approx 8.6%$
4. $frac{78-76}{76} approx 2.6%$
5. $frac{85-78}{78} approx 9%$
The answer is $mathrm{(A)}$ .
After paying his taxes, he has $0.8*0.9=0.72$ of his earnings left. Since $10500$ is $0.28$ of his income, he got a total of $frac{10500}{0.28}=37500 mathrm{(D)}$ .
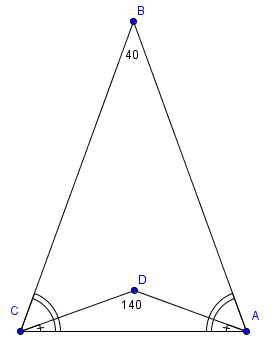We angle chase, and find out that:
- $DAC=frac{180-140}{2} = 20$
- $BAC=frac{180-40}{2} = 70$
- $BAD=BAC-DAC=50 mathrm{(D)}$
Since triangle $ABC$ is isosceles we know that angle $angle BAC = angle BCA$ .

Also since triangle $ADC$ is isosceles we know that $angle DAC = angle DCA$ .

This implies that $angle BAD = angle BCD$ .

Then the sum of the angles in quadrilateral $ABCD$ is $40 + 220 + 2angle BAD = 360$ .

Solving the equation we get $angle BAD = 50$ .

Therefore the answer is (D).
$[81^{b+2} = 3^{4(b+2)} = 3^a Longrightarrow a = 4b+8]$ And $[125^{b} = 5^{3b} = 5^{a-3} Longrightarrow a - 3 = 3b]$ Substitution gives $4b+8 - 3 = 3b Longrightarrow b = -5$ , and solving for $a$ yields $-12$ . Thus $ab = 60 mathrm{(E)}$ .Simplify equation $1$ which is $3^a=81^{b+2}$ , to $3^a=3^{4b+8}$ .AndSimplify equation $2$ which is $125^b=5^{a-3}$ , to $5^{3b}=5^{a-3}$ .
Now, eliminate the bases from the simplified equations $1$ and $2$ to arrive at $a=4b+8$ and $3b=a-3$ . Rewrite equation $2$ so that it is in terms of $a$ . That would be $a=3b+3$ .

Since both equations are equal to $a$ , and $a$ and $b$ are the same number for both problems, set the equations equal to each other. $4b+8=3b+3$ $b=-5$

Now plug $b$ , which is $(-5)$ back into one of the two earlier equations. $4(-5)+8=a$ $-20+8=a$ $a=-12$

$(-12)(-5)=60$

Therefore the correct answer is E
Let $n$ be the number of children. Then the total ages of the family is $48 + 16(n+1)$ , and the total number of people in the family is $n+2$ . So $[20 = frac{48 + 16(n+1)}{n+2} Longrightarrow 20n + 40 = 16n + 64 Longrightarrow n = 6 mathrm{(E)}.]$ Let x be number of children+the mom. The father, who is 48, plus the number of kids and mom divided by the number of kids and mom plus 1 (for the dad)=20. This is because the average age of the entire family is 20. Basically, this looks like 48+16x/x+1=20 $48+16x=20x+20 4x=28 x=7$ 7 people - 1 mom = 6 children.E is the answer
The sum of the numbers on the top face of a cube is equal to the sum of the numbers on the bottom face of the cube; these $8$ numbers represent all of the vertices of the cube. Thus the answer is $frac{1 + 2 + cdots + 8}{2} = 18 mathrm{(C)}$ .Consider a number on a vertex. It will be counted in 3 different faces, the ones it is on. Therefore, each number $1,2,cdots,7,8$ will be added into the total sum $3$ times. Therefore, our total sum is $3(1+2+cdots+8)=108.$ Finally, since there are $6$ faces, our common sum is $dfrac{108}{6}=mathrm{(C) } 18.$
Each tourist has to pick in between the $2$ guides, so for $6$ tourists there are $2^6$ possible groupings. However, since each guide must take at least one tourist, we subtract the $2$ cases where a guide has no tourist. Thus the answer is $2^6 - 2 = 62 mathrm{(D)}$ .
Let the distance from Yan's initial position to the stadium be $a$ and the distance from Yan's initial position to home be $b$ . We are trying to find $b/a$ , and we have the following identity given by the problem: $begin{align*}a &= b + frac{a+b}{7}\ frac{6a}{7} &= frac{8b}{7} Longrightarrow 6a = 8bend{align*}$ Thus $b/a = 6/8 = 3/4$ and the answer is $mathrm{(B)} frac{3}{4}$ Another way of solving this problem is by setting the distance between Yan's home and the stadium, thus filling in one variable. Let us set the distance between the two places to be $42z$ , where $z$ is a random measurement (cause life, why not?) The distance to going to his home then riding his bike, which is $7$ times faster, is equal to him just walking to the stadium. So the equation would be: Let $x=$ the distance from Yan's position to his home. Let $42z=$ the distance from Yan's home to the stadium. $42-x=x+42/7$ $42-x=x+6$ $36=2x$
$x=18$

But we're still not done with the question. We know that Yan is $18z$ from his home, and is $42z-18z$ or $24z$ from the stadium. $18z/24z$ , the $z$ 's cancel out, and we are left with $3/4$ . Thus, the answer is $mathrm{(B)} frac{3}{4}$

~ProGameXD

Assume that the distance from the home and stadium is 1, and the distance from Yan to home is $b$ . Also assume that the speed of walking is 1, so the speed of biking is 7. Thus $1-b=b+1/7$ $b=3/7$ We need $b/1-b$

$3/7$ divided by $4/7$ = $mathrm{(B)} frac{3}{4}$
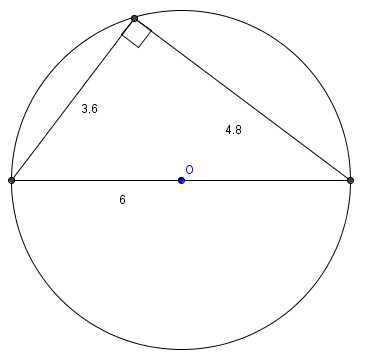Since 3-4-5 is a Pythagorean triple, the triangle is a right triangle. Since the hypotenuse is a diameter of the circumcircle, the hypotenuse is $2r = 6$ . Then the other legs are $frac{24}5=4.8$ and $frac{18}5=3.6$ . The area is $frac{4.8 cdot 3.6}2 = 8.64 mathrm{(A)}$
Draw a square connecting the centers of the four small circles of radius $1$ . This square has a diagonal of length $6$ , as it includes the diameter of the big circle of radius $2$ and two radii of the small circles of radius $1$ . Therefore, the side length of this square is $[frac{6}{sqrt{2}} = 3sqrt{2}.]$ The radius of the large square has a side length $2$ units larger than the one found by connecting the midpoints, so its side length is $[2 + 3sqrt{2}.]$ The area of this square is $(2+3sqrt{2})^2 = 22 + 12sqrt{2}$ $(B).$
The only times when $ad-bc$ is even is when $ad$ and $bc$ are of the same parity. The chance of $ad$ being odd is $frac 12 cdot frac 12 = frac 14$ , so it has a $frac 34$ probability of being even. Therefore, the probability that $ad-bc$ will be even is $left(frac 14right)^2+left(frac 34right)^2=frac 58 mathrm{(E)}$ .
$3 cdot 5^2m$ must be a perfect cube, so each power of a prime in the factorization for $3 cdot 5^2m$ must be divisible by $3$ . Thus the minimum value of $m$ is $3^2 cdot 5 = 45$ , which makes $n = sqrt[3]{3^3 cdot 5^3} = 15$ . These sum to $60 mathrm{(D)}$ .
We can obtain the solution by calculating the area of rectangle $ABGH$ minus the combined area of triangles $triangle AHG$ and $triangle CGM$ .We know that triangles $triangle AMH$ and $triangle GMC$ are similar because $overline{AH} parallel overline{CG}$ . Also, since $frac{AH}{CG} = frac{3}{2}$ , the ratio of the distance from $M$ to $overline{AH}$ to the distance from $M$ to $overline{CG}$ is also $frac{3}{2}$ . Solving with the fact that the distance from $overline{AH}$ to $overline{CG}$ is 4, we see that the distance from $M$ to $overline{CG}$ is $frac{8}{5}$ .The area of $triangle AHG$ is simply $frac{1}{2} cdot 4 cdot 12 = 24$ , the area of $triangle CGM$ is $frac{1}{2} cdot frac{8}{5} cdot 8 = frac{32}{5}$ , and the area of rectangle $ABGH$ is $4 cdot 12 = 48$ .Taking the area of rectangle $ABGH$ and subtracting the combined area of $triangle AHG$ and $triangle CGM$ yields $48 - (24 + frac{32}{5}) = boxed{frac{88}{5}} text{(C)}$ . $[asy] unitsize(2cm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=4; pair A=(1,3), B=(2,3), C=(2,2), D=(3,2), Ep=(3,1), F=(2,1), G=(2,0), H=(1,0), I=(1,1), J=(0,1), K=(0,2), L=(1,2); pair M=intersectionpoints(A--G,H--C)[0]; pair Z=(2.5,3); draw(A--B--C--D--Ep--F--G--H--I--J--K--L--cycle); draw(A--G); draw(H--C); draw(B--Z--C); draw(C--F); dot(M); label("$A$",A,NW); label("$B$",B,N); label("$C$",C,SE); label("$D$",D,NE); label("$E$",Ep,SE); label("$F$",F,SE); label("$G$",G,SE); label("$H$",H,SW); label("$I$",I,SW); label("$J$",J,SW); label("$K$",K,NW); label("$L$",L,NW); label("$M$",M,W); label("$N$",Z,NE); [/asy]$ Extend $AB$ and $CH$ and call their intersection $N$ .The triangles $CBN$ and $CGH$ are clearly similar with ratio $1:2$ , hence $BN=2$ and thus $AN=6$ . The area of the triangle $BCN$ is $frac{2cdot 4}2 = 4$ .
The triangles $MAN$ and $MGH$ are similar as well, and we now know that the ratio of their dimensions is $AN:GH = 6:4 = 3:2$ .

Draw altitudes from $M$ onto $AN$ and $GH$ , let their feet be $M_1$ and $M_2$ . We get that $MM_1 : MM_2 = 3:2$ . Hence $MM_1 = frac 35 cdot 12 = frac {36}5$ . (An alternate way is by seeing that the set-up AHGCM is similar to the 2 pole problem. Therefore, $MM_2$ must be $frac{1}{frac{1}{8}+frac{1}{12}} = frac{24}{5}$ , by the harmonic mean. Thus, $MM_1$ must be $frac{36}{5}$ .)

Then the area of $AMN$ is $frac 12 cdot AN cdot MM_1 = frac{108}5$ , and the area of $ABCM$ can be obtained by subtracting the area of $BCN$ , which is $4$ . Hence the answer is $frac{108}5 - 4 = boxed{frac{88}5}$ .

$[asy] unitsize(13mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=4; pair A=(1,3), B=(2,3), C=(2,2), D=(3,2), Ep=(3,1), F=(2,1), G=(2,0), H=(1,0), I=(1,1), J=(0,1), K=(0,2), L=(1,2); pair M=intersectionpoints(A--G,H--C)[0]; draw(A--B--C--D--Ep--F--G--H--I--J--K--L--cycle); draw(A--G); draw(H--C); dot(M); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,NE); label("$D$",D,NE); label("$E$",Ep,SE); label("$F$",F,SE); label("$G$",G,SE); label("$H$",H,SW); label("$I$",I,SW); label("$J$",J,SW); label("$K$",K,NW); label("$L$",L,NW); label("$M$",M,W); [/asy]$

We can use coordinates to solve this. Let $H=(0,0).$ Thus, we have $A=(0,12), C=(4,8), G=(4,0).$ Therefore, $AG$ has equation $-3x+12=y$ and $HC$ has equation $2x=y.$ Solving, we have $M=(12/5,24/5).$ Using Shoelace Theorem (or you could connect $LC$ and solve for the resulting triangle + trapezoid areas), we find $[ABCM]=boxed{mathrm{(C) }dfrac{88}{5}}.$
Without loss of generality, let the side length of the square be $1$ unit. The area of the painted area is $frac{1}2$ of the area of the larger square, so the total unpainted area is also $frac{1}{2}$ . Each of the $4$ unpainted triangle has area $frac{1}8$ . It is easy to tell that these triangles are isosceles right triangles, so let $a$ be the side length of one of the smaller triangles: $frac{a^2}2 = frac{1}8 rightarrow a= frac{1}2$ The hypotenuse of the triangle is $frac{sqrt{2}}2$ . The corners of the painted areas are also isosceles right triangles with side length $frac{1-frac{sqrt{2}}2}2 = frac{1}2-frac{sqrt2}4$ . Its hypotenuse is equal to the width of the paint, and is $frac{sqrt{2}}2-frac{1}2$ . The answer we are looking for is thus $frac{1}{frac{sqrt{2}}2-frac{1}2}$ . Multiply the numerator and the denominator by $frac{sqrt{2}}2+frac{1}2$ to simplify, and you get $frac{frac{sqrt{2}}{2}+frac{1}{2}}{frac{2}{4}-frac{1}{4}}$ or $4left(frac{sqrt{2}}{2}+frac{1}{2}right)$ which is $boxed{2sqrt{2}+2} rightarrow C$ .Again, have the length of the square equal to $1$ and let the width of each individual stripe be $n$ . Note that you can split each stripe into two rectangles and two isosceles right triangles at the corners. Then the area of each stripe is $n(sqrt{2}-frac{n}{2})=sqrt{2}n-frac{n^2}{2}$ . The area covered by the two total stripes is twice the area of one stripe, minus the area in the intersection of the stripes, which is a square with side length $n$ . This area is equal to $frac{1}{2}$ So: $2sqrt2n-2n^2=frac{1}{2}rightarrow-2n^2+2sqrt2n-frac{1}{2}=0$ .By the quadratic formula, $n=frac{-2sqrt{2}pmsqrt{(2sqrt{2})^2-4(-2)(-frac{1}{2})}}{2(-2)}rightarrow n=frac{-2sqrt{2}pm 2}{-4}rightarrow n=frac{sqrt{2}pm 1}{2}$ It's easy to tell that $frac{sqrt{2}+1}{2}$ is too large, so $n=frac{sqrt{2}-1}{2}$ . We want to find $frac{1}{n}$ , and $frac{1}{n}=frac{2}{sqrt{2}-1}$ . Multiply the numerator and the denominator by $sqrt{2}+1$ , $frac{1}{n}=frac{2(sqrt{2}+1)}{(sqrt{2}-1)(sqrt{2}+1)}=boxed{2sqrt{2}+2}rightarrow C$
Notice that $(a^{k} + a^{-k})^2 = a^{2k} + a^{-2k} + 2$ . Thus $a^4 + a^{-4} = (a^2 + a^{-2})^2 - 2 = [(a + a^{-1})^2 - 2]^2 - 2 = 194 mathrm{(D)}$ . $4a = a^2 + 1$ . We apply the quadratic formula to get $a = frac{4 pm sqrt{12}}{2} = 2 pm sqrt{3}$ .Thus $a^4 + a^{-4} = (2+sqrt{3})^4 + frac{1}{(2+sqrt{3})^4} = (2+sqrt{3})^4 + (2-sqrt{3})^4$ (so it doesn't matter which root of $a$ we use). Using the binomial theorem we can expand this out and collect terms to get $194$ .(similar to Solution 1) We know that $a+frac{1}{a}=4$ . We can square both sides to get $a^2+frac{1}{a^2}+2=16$ , so $a^2+frac{1}{a^2}=14$ . Squaring both sides again gives $a^4+frac{1}{a^4}+2=14^2=196$ , so $a^4+frac{1}{a^4}=boxed{194}$ .We let $a$ and $1/a$ be roots of a certain quadratic. Specifically $x^2-4x+1=0$ . We use Newton's Sums given the coefficients to find $S_4$ . $S_4=boxed{194}$ Let $a$ = $cos(x)$ + $isin(x)$ . Then $a + a^{-1} = 2cos(x)$ so $cos(x) = 2$ . Then by De Moivre's Theorem, $a^4 + a^{-4}$ = $2cos(4x)$ and solving gets 194.
$[asy] import three; draw(((0,0,0)--(0,1,0)--(1,1,0)--(1,0,0)--(0,0,0))^^((0,0,1)--(0,1,1)--(1,1,1)--(1,0,1)--(0,0,1))^^((0,0,0)--(0,0,1))^^((0,1,0)--(0,1,1))^^((1,1,0)--(1,1,1))^^((1,0,0)--(1,0,1))); draw(shift((0.5,0.5,0.5))*scale3(1/sqrt(3))*shift((-0.5,-0.5,-0.5))*rotate(aTan(sqrt(2)),(0,0,0.5),(1,1,0.5))*(((0,0,0)--(0,1,0)--(1,1,0)--(1,0,0)--(0,0,0))^^((0,0,1)--(0,1,1)--(1,1,1)--(1,0,1)--(0,0,1))^^((0,0,0)--(0,0,1))^^((0,1,0)--(0,1,1))^^((1,1,0)--(1,1,1))^^((1,0,0)--(1,0,1)))); dot((0.5,0.5,1)^^(0.5,0.5,0)); [/asy]$ We rotate the smaller cube around the sphere such that two opposite vertices of the cube are on opposite faces of the larger cube. Thus the main diagonal of the smaller cube is the side length of the outer square.

Let $S$ be the surface area of the inner square. The ratio of the areas of two similar figures is equal to the square of the ratio of their sides. As the diagonal of a cube has length $ssqrt{3}$ where $s$ is a side of the cube, the ratio of a side of the inner square to that of the outer square (and the side of the outer square = the diagonal of the inner square), we have $frac{S}{24} = left(frac{1}{sqrt{3}}right)^2$ . Thus $S = 8Rightarrow mathrm{boxed{(C)}}$ .

The area of each face of the outer cube is $frac {24}{6} = 4$ , and the edge length of the outer cube is $2$ . This is also the diameter of the sphere, and thus the length of a long diagonal of the inner cube.

A long diagonal of a cube is the hypotenuse of a right triangle with a side of the cube and a face diagonal of the cube as legs. If a side of the cube is $x$ , we see that $2 = sqrt {x^{2} + (sqrt {2}x)^{2}}Rightarrow x = frac {2}{sqrt {3}}$ .

Thus the surface area of the inner cube is $6x^{2} = 6left(frac {2}{sqrt {3}}right )^{2} = 8$ .

Since the surface area of the original cube is 24 square meters, each face of the cube has a surface area of $24/6 = 4$ square meters, and the side length of this cube is 2 meters. The sphere inscribed within the cube has diameter 2 meters, which is also the length of the diagonal of the cube inscribed in the sphere. Let $l$ represent the side length of the inscribed cube. Applying the Pythagorean Theorem twice gives $[l^2 + l^2 + l^2 = 2^2 = 4.]$ Hence each face has surface area $[l^2 = frac{4}{3} text{square meters}.]$ So the surface area of the inscribed cube is $6cdot (4/3) = boxed{8}$ square meters.
A given digit appears as the hundreds digit, the tens digit, and the units digit of a term the same number of times. Let $k$ be the sum of the units digits in all the terms. Then $S=111k=3*37k$ , so $S$ must be divisible by $37 mathrm{(D)}$ . To see that it need not be divisible by any larger prime, the sequence $123, 231, 312$ gives $S=666=2 cdot 3^2 cdot 37Rightarrow mathrm{boxed{(D)}}$ .
$[m^2 - n^2 = (m+n)(m-n) = 96 = 2^{5} cdot 3]$ For every two factors $xy = 96$ , we have $m+n=x, m-n=y Longrightarrow m = frac{x+y}{2}, n = frac{x-y}{2}$ . Since $m ge n > 0$ , $x+y ge x-y > 0$ , from which it follows that the number of ordered pairs $(m,n)$ is given by the number of ordered pairs $(x,y): xy=96, x > y > 0$ . There are $(5+1)(1+1) = 12$ factors of $96$ , which give us six pairs $(x,y)$ . However, since $m,n$ are positive integers, we also need that $frac{x+y}{2}, frac{x-y}{2}$ are positive integers, so $x$ and $y$ must have the same parity. Thus we exclude the factors $(x,y) = (1,96)(3,32)$ , and we are left with four pairs $mathrm{(B)}$ .Similar to the solution above, reduce $96$ to $2^5*3^1$ . To find the number of distinct prime factors, add $1$ to both exponents and multiply, which gives us $6*2=12$ factors. Divide by $2$ since $m$ must be greater than or equal to $n$ . We don't need to worry about $m$ and $n$ being equal because $96$ is not a square number. Finally, subtract the two cases above for the same reason to get $mathrm{(B)}$ .
The area we are trying to find is simply $ABFE-(overarc{AEC}+triangle{ACO}+triangle{BDO}+overarc{BFD})$ . Obviously, $overline{EF}paralleloverline{AB}$ . Thus, $ABFE$ is a rectangle, and so its area is $btimes{h}=2times{(AO+OB)}=2times{2(2sqrt{2})}=8sqrt{2}$ .Since $overline{OC}$ is tangent to circle $A$ , $triangle{ACO}$ is a right triangle. We know $AO=2sqrt{2}$ and $AC=2$ , so $triangle{ACO}$ is isosceles, a $45$ - $45$ right triangle, and has $overline{CO}$ with length $2$ . The area of $triangle{ACO}=frac{1}{2}bh=2$ . By symmetry, $triangle{ACO}congtriangle{BDO}$ , and so the area of $triangle{BDO}$ is also $2$ . $overarc{AEC}$ (or $overarc{BFD}$ , for that matter) is $frac{1}{8}$ the area of its circle. Thus $overarc{AEC}$ and $overarc{BFD}$ both have an area of $frac{pi}{2}$ .Plugging all of these areas back into the original equation yields $8sqrt{2}-(frac{pi}{2}+2+2+frac{pi}{2})=8sqrt{2}-(4+pi)=boxed{8sqrt{2}-4-pi} mathrm{(B)}$ .
For the sake of notation let . Obviously . Then the maximum value of is when , and the sum becomes . So the minimum bound is . We do casework upon the tens digit:Case 1: . Easy to directly disprove.Case 2: . , and if and otherwise.

Subcase a: $T(n) = 1970 + u + 17 + u + 8 + u = 1995 + 3u = 2007 Longrightarrow u = 4$ . This exceeds our bounds, so no solution here.

Subcase b: $T(n) = 1970 + u + 17 + u + u - 1 = 1986 + 3u = 2007 Longrightarrow u = 7$ . First solution.

Case 3: $198u$ . $S(n) = 18 + u$ , and $S(S(n)) = 9 + u$ if $u le 1$ and $2 + (u-2) = u$ otherwise.

Subcase a: $T(n) = 1980 + u + 18 + u + 9 + u = 2007 + 3u = 2007 Longrightarrow u = 0$ . Second solution.

Subcase b: $T(n) = 1980 + u + 18 + u + u = 1998 + 3u = 2007 Longrightarrow u = 3$ . Third solution.

Case 4: $199u$ . But $S(n) > 19$ , and $n + S(n)$ clearly sum to $> 2007$ .

Case 5: $200u$ . So $S(n) = 2 + u$ and $S(S(n)) = 2 + u$ (recall that $n < 2007$ ), and $2000 + u + 2 + u + 2 + u = 2004 + 3u = 2007 Longrightarrow u = 1$ . Fourth solution.

In total we have $4 mathrm{(D)}$ solutions, which are $1977, 1980, 1983,$ and $2001$ .

Clearly, $n > 1950$ . We can break this into three cases:

Case 1: $n geq 2000$

Inspection gives $n = 2001$ .

Case 2: $n < 2000$ , $n = 19xy$ (not to be confused with $19*x*y$ ), $x + y < 10$

If you set up an equation, it reduces to

$4x + y = 32$

which has as its only solution satisfying the constraints $x = 8$ , $y = 0$ .

Case 3: $n < 2000$ , $n = 19xy$ , $x + y geq 10$

This reduces to

$4x + y = 35$ . The only two solutions satisfying the constraints for this equation are $x = 7$ , $y = 7$ and $x = 8$ , $y = 3$ .

The solutions are thus $1977, 1980, 1983, 2001$ and the answer is $mathrm{(D)} 4$ .

As in Solution 1, we note that $S(n)leq 28$ and $S(S(n))leq 10$ .
Obviously, $nequiv S(n)equiv S(S(n)) pmod 9$ .
As $2007equiv 0 pmod 9$ , this means that $nbmod 9 in{0,3,6}$ , or equivalently that $nequiv S(n)equiv S(S(n))equiv 0 pmod 3$ .

Thus $S(S(n))in{3,6,9}$ . For each possible $S(S(n))$ we get three possible $S(n)$ .
(E. g., if $S(S(n))=6$ , then $S(n)=x$ is a number such that $xleq 28$ and $S(x)=6$ , therefore $S(n)in{6,15,24}$ .)

For each of these nine possibilities we compute $n_{?}$ as $2007-S(n)-S(S(n))$ and check whether $S(n_{?})=S(n)$ .
We'll find out that out of the 9 cases, in 4 the value $n_{?}$ has the correct sum of digits.
This happens for $n_{?}in { 1977, 1980, 1983, 2001 }$ .
- This solution is not a good solution, but is viable for in contest situations
Clearly $nequiv S(n) pmod 9$ . Thus, $[n+S(n)+S(S(n))equiv 0 pmod 9 implies nequiv 0pmod 3.]$ Now we need a bound for $n$ . It is clear that the maximum for $S(n)=36$ (from $n=9999$ ) which means the maximum for $S(n)+S(S(n))$ is $45$ . This means that $ngeq 1962$ .
- Warning: This is where you will cringe badly
Now check all multiples of $3$ from $1962$ to $2007$ and we find that only $n=1977, 1980, 1983, 2001$ work, so our answer is $mathrm{(D)} 4$ .

Remark: this may seem time consuming, but in reality, calculating $n+S(n)+S(S(n))$ for $16$ values is actually very quick, so this solution would only take approximately 3-5 minutes, helpful in a contest.